9.6 最小二乘拟合

相关系数可以衡量两个变量之间线性相关的强度和正负，但是无法知道它们的斜率。有很多方法可以用来估计斜率，其中线性最小二乘拟合（linear least square fit）是最常用的一种方法。线性拟合（linear fit）指的是用一个线性的方程来拟合两个变量之间的关系。最小二乘法（least square）是使拟合函数与数据之间的均方误差达到最小的拟合方法^〔1〕。

^〔1〕参见http://wikipedia.org/wiki/Simple_linear_regression。

假设我们有一个数据序列X，要通过X的一个函数来预测另一个数据序列Y。如果这个预测函数是线性的，截距为α，斜率为β，那么我们可以预期y_i大约会等于α+βx_i。

除非这两个序列是完全线性相关的，否则我们只能近似地预测Y的值。预测的离差(或称残差)为：

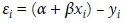
残差的出现可能是由数据测量误差造成的，也可能是一些我们未知的非随机因素引起的。例如，当我们通过身高的一个函数来预测体重时，这些未知的因素可能就包括饮食、身体锻炼情况和体型等。

假设两个变量存在这样的一个线性关系，那么如果我们错误地估计了参数α和β，就会造成很大的残差。所以，这些参数自然应该使得残差尽可能地小。

一般地，可以通过最小化残差的绝对值、平方、立方等来求解参数。实际中最通用的方法是使残差的平方和最小，即

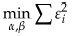
我们解释一下这个选择的原因。

• 平方能将正残差和负残差都变成正数，这符合我们的目标。
• 平方相当于给残差赋予了一个权重，越大的残差（绝对量）被赋予的权重越大。但是并不是所有情况下大的残差都应该被赋予大的权重，因为这样拟合方程就很容易受到异常值的影响。
• 在残差服从均值为0、方差为σ2（未知，但为常数）的正态分布，且在残差与x独立的假设下，参数的最小二乘估计结果与极大似然估计量相同。 〔2〕
• 最小二乘估计的计算非常简单。

^〔2〕请参考Press等人合著的 Numerical Recipes in C第15章：http://t.cn/zYeSWUm。

就现在而言，除非在某些计算效率比方法更重要的情况下，否则上述最后一个原因已经不再那么具有吸引力了。所以更多时候要思考的是，就我们的问题而言最小二乘是否是最适合的方法。

例如，我们用X来预测Y。如果预测结果偏高造成的代价远低于预测结果偏低造成的代价，那么构造一个损失函数cost(ε_i)，并最小化损失函数会是一个更好的选择。

接下来我们介绍如何进行最小二乘拟合。

• 计算两个序列的均值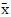和，X的方差，X和Y的协方差。

• 估计斜率

  

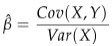
• 估计截距

  

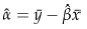
读者可以从http://wikipedia.org/wiki/Numerical_methods_for_linear_least_squares了解公式的推导过程。

习题9-5

请编写一个名为LeastSquares的函数，用来估计X和Y的回归系数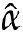和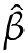。可以从http://thinkstats.com/correlation.py下载到问题的答案。

习题9-6

在BRFSS的数据中，请用身高对体重的对数进行最小二乘拟合。可以从http://thinkstats.com/brfss_corr.py下载到问题的答案。

习题9-7

某个地点风速的分布决定了该地点的风能密度。风能密度是安装在该位置的风力涡轮机所能产生的平均功率的上限。根据之前的一些研究，风速的经验分布非常接近威布尔分布（参考http://wikipedia.org/wiki/Wind_power#Distribution_of_wind_speed）。

为了评估某个地方是否有安装风力涡轮机的价值，我们可以在这个地方设置一个风力计来测量一段时间内的风速。但很难测量到风速分布的尾巴，因为可以认为这是一个小概率事情，一般不大可能在一次试验中被观测到。

一种解决这个问题的方法是，我们先估计威布尔分布的参数，再对分布求积分计算风能密度。

为了估计威布尔分布的参数，可以用习题4-6中的变换方法，然后用最小二乘拟合来计算变换数据的斜率和截距。

请编写一个从威布尔分布中抽取样本并估计分布参数的函数。

最后请编写一个利用威布尔分布参数计算平均风能密度的函数。（这里你可能需要了解一下风力方面的专业知识。）