3.4 累积分布函数

理解了百分位数，现在我们可以开始学习累积分布函数（CDF）了。CDF函数就是值到其在分布中百分等级的映射。

CDF是x的函数，其中x是分布中的某个值。计算给定x的CDF(ｘ)，就是计算样本中小于等于x的值的比例。

以下函数的参数是样本t和值x：

  1.     def Cdf(t, x): 
  2.         count = 0.0 
  3.         for value in t: 
  4.             if value <= x: 
  5.                 count += 1.0
  7.         prob = count / len(t) 
  8.         return prob

读者应该很熟悉这个函数，这跟前面的PercentileRank函数几乎一样，唯一区别就是该函数返回的结果是0～1范围内的概率，而不是0～100范围内的百分等级。

来看个例子，给定一个样本{1, 2, 2, 3, 5}。下面是其中某些值的CDF：

  1. CDF(0) = 0 
  2. CDF(1) = 0.2 
  3. CDF(2) = 0.6 
  4. CDF(3) = 0.8 
  5. CDF(4) = 0.8 
  6. CDF(5) = 1

我们可以计算任意值x的CDF，而不仅是样本中出现的值。如果x比样本中最小的值还要小，那么CDF(x)就等于0。如果x比样本中的最大值还要大，那么CDF(x)就是1。

图3-2是这个CDF的图形化表示。样本的CDF是一个阶梯函数。在下一章，我们会看到作为连续函数的CDF的分布。

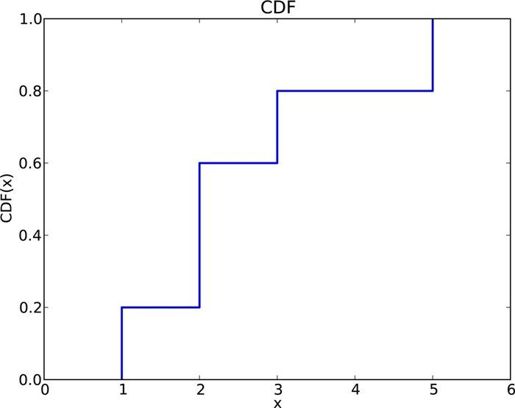
enter image description here

图3-2 CDF示例