8.4 指数分布

还是那个游戏，但现在我想到的是指数分布，并且得到了一组样本：

{5.384, 4.493, 19.198, 2.790, 6.122, 12.844}

那么这里指数分布的参数λ会是多少呢？

因为指数分布的均值为1/λ，所以根据之前的处理，我们会选择如下的估计量来估计λ：

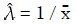
一般情况下，我们给待估的参数上加一个帽子，以此来表示这个参数的估计量。这里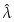不仅是λ的估计量而且还是它的极大似然估计量，^〔1〕所以如果我们想要有最大的可能性猜对λ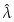，是最好的选择。

^〔1〕参见http://wikipedia.org/wiki/Exponential_distribution#Maximum_likelihood。

但是我们出现异常值时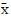，的鲁棒性不好，所以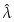也会面临同样的问题。

这里可以用另一种基于中位数的方法来估计λ。我们知道指数分布的中位数等于log(2)/λ，于是根据前面的做法，定义λ的估计量为：

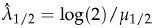
这里μ_1/2表示的是样本的中位数。

习题8-3

请通过模拟比较一下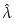和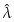_1/2的均方误差哪个更低，并检查这两个估计量是否是有偏的。