6.4 卷积

设两个随机变量X和Y的累积分布函数分别为CDF_X和CDF_Y，Z=X+Y，那么Z服从什么分布呢？

一种简单的估算Z的分布的方法是编写一个RandomVariable对象，产生一些X和Y，然后将它们加起来。下面是这种方法的代码实现：

class Sum(RandomVariable):
    def __init__(X, Y):
        self.X = X
        self.Y = Y
    def generate():
        return X.generate() + Y.generate()

我们可以产生很多Z的随机数，然后估计CDF_Z。

上述方法是一个非常简单直观的方法，但不是很有效。为了能对CDF_Z有一个较准确的估计，我们必须产生大量的X和Y的随机数。而且不管这个精度被提高到什么程度，它总归不是Z的真实分布。

假设随机变量X和Y的累积分布函数CDF_X和CDF_Y有解析表达式，在某些情况下我们可以通过数学推导得到CDF_Z的解析表达式。

接下来介绍公式推导过程。

• 从最简单的情况出发，假设随机变量X只能某个值x，这时CDFZ(z)等于

P (Z≤z|X=x) = P(Y≤z-x)

上述等式的左半部分表示的是“在给定X=x的条件下，X+Y小于z的概率”。显然，要使X+Y小于z，就要求Y必须小于z-x。

• 接下来，我们计算Y小于z-x的概率，根据Y的累积分布函数有

P(Y≤z-x) = CDFY(z-x)

• 上述推导过程假设X取某个固定值，但实际上它是一个随机变量。所以，我们还必须考虑X在其取值范围内的所有情况，于是：

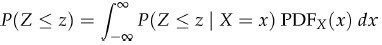
被积函数等于“给定X=x的条件下，随机变量Z小于等于z的概率乘以X=x的概率”。

将前面两步的结果带入公式，有

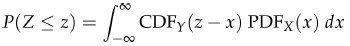
等式左边就是CDFZ的定义，整理可得：

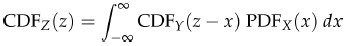
• 我们可以通过对CDFZ求导得到PDFZ，结果如下：

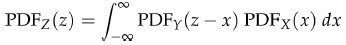
如果读者之前学过信号与系统等课程，或许对这个积分公式不会感到陌生。它表示的是概率密度函数PDF_X和PDF_Y的卷积（convolution）。卷积运算一般用运算符*表示。

PDF_Z = PDF_Y*PDF_X

综上可知，两个随机变量的和的分布就等于两个概率密度的卷积。参考 http://wiktionary.org/wiki/booyah!

下面我们通过一个例子来说明如何计算。设随机变量X和Y服从参数为λ的指数分布，则随机变量Z=X+Y的概率密度为：

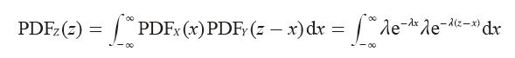
因为X和Y服从指数分布，它们取负数的概率为0，所以我们可以对上述积分公式的下限进行调整：

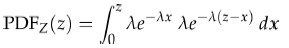
整理可得：

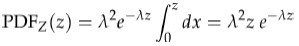
这是参数为k和λ的爱尔朗分布的概率密度函数，这里k=2。所以两个有相同参数的指数分布的卷积是一个爱尔朗分布。爱尔朗分布参考 http://en.wikipedia.org/wiki/Erlang_distribution 。

习题6-7

假设随机变量X服从参数为λ的指数分布，Y服从参数为k和λ的爱尔朗分布，Z=X+Y，那么Z服从什么分布呢？

习题6-8

假设我们从一个分布中抽取两个样本X₁和X₂，Y=max(X₁, X₂)，那么Y服从什么分布呢？请分别用PDF和CDF的形式表示。

随着值数量的增多，最大值的分布会收敛到某个极值的分布，参考http://wikipedia.org/wiki/Gumbel_distribution。

习题6-9

假设我们有随机变量X和Y的Pmf，Z=X+Y，那么就可以通过枚举法得到Z所有可能的取值：

for x in pmf_x.Values():
    for y in pmf_y.Values():
        z = x + y

请编写一个关于PMF_X和PMF_Y的函数，用于计算Z的PMF。

请再编写一个类似的函数，用于计算max(X,Y)的PMF。