4.2 帕累托分布

帕累托分布是以经济学家Vilfredo Pareto（维尔弗雷多·帕累托）的名字命名的，他曾用这个分布来描述财富分布情况（详见http://wikipedia.org/wiki/Pareto_distribution）。从那以后，该分布就广泛用于描述自然界和社会科学中的各种现象，包括城镇大小、砂粒和陨石、森林火灾和地震等。

帕累托分布的CDF是：

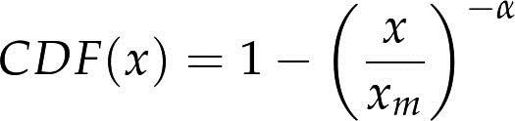
参数x_m和α决定了分布的位置和形状。x_m是最小值。图4-4是x_m=0.5、α=1的帕累托分布的CDF。

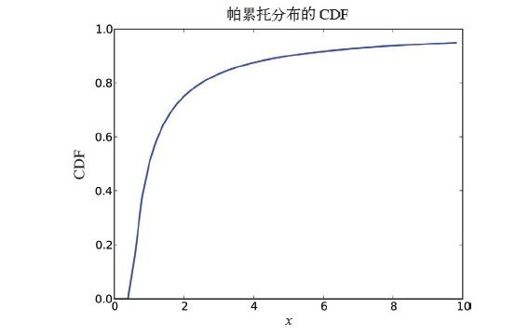
图4-4 帕累托分布的CDF

该分布的中位数是：

x_m2^1/α

即1，但其百分等级为95的值是10，而中位数为1的指数分布中百分等级为95的值仅仅是1.5。

可以通过图形判断一个经验分布是否服从帕累托分布：对两条数轴都取对数后，其CCDF应该基本上是一条直线。如果直接画出服从帕累托分布的样本的CCDF，其函数如下：

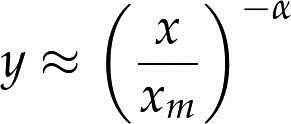
对两边取对数：

log y ≈ -α(log x - log x_m)

在对y和x取对数后，就应该基本上是条直线，斜率是−α，截距是 −αlogx_m。

习题4-3

random模块中的paretovariate函数可以生成服从帕累托分布的随机数。该函数只有一个参数α，却没有x_m。x_m默认值是1，乘上x_m，就可以生成各种不同的分布。

写一个paretovariate函数，以α和x_m作为参数，用random.paretovariate生成服从双参数帕累托分布的随机数。

用你自己编写的函数生成一个服从帕累托分布的样本。计算CCDF，取对数后画出来。是一条直线吗？斜率是多少？

习题4-4

为了对帕累托分布有一个直观感受，让我们想象一下，如果全世界所有的人的身高服从帕累托分布会是一个什么情况。假设参数x_m=100厘米，α=1.7。这个分布的最小值是100厘米，而中位数是150厘米（这样比较合理）。

生成60亿个服从该分布的随机值。样本的均值是多少？其中有多大比例的人身高低于均值？在帕累托世界中最高的人多高？

习题4-5

Zipf法则是一个关于各种单词使用频率差异的观察结论。常用单词的使用频率非常高，而罕见单词比如hapaxlegomenon（一次频词）则使用得很少。 Zipf法则说的是在一段文本（即语料库corpus）中，单词频率的分布近似于帕累托分布。

找一个大的电子版语料库，任何语言的都可以。计算其中每个单词的出现次数。算出单词出现次数的CCDF，画出取对数后的图。Zipf法则是否成立？α的近似值是多少？

习题4-6

威布尔分布是一个广义上的指数分布，源自故障分析（failure analysis，详见http://wikipedia.org/wiki/Weibull_distribution）。它的CDF是：

CDF(x) = 1-e ^-(x/λ)k

能否找到某个变换将威布尔分布变成一条直线？这条直线的斜率和截距分别表示什么意思？

用random.weibullvariate生成一个服从威布尔分布的样本，然后用这个样本测试一下你的变换。