6.3 概率密度函数

累积分布函数的导数称为概率密度函数（probability density function），简记为PDF。例如， 指数分布的概率密度函数为：

PDF_expo(x) = λe^-λx

正态分布的概率密度函数为：

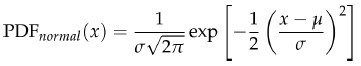
概率密度函数的值并不是概率，它表示的是一种概率密度（probability density）。

物理学中，密度指的是单位体积内物质所拥有的质量，质量就等于体积乘以密度。如果物体的密度不固定，即不同部位密度不同，那么我们可以通过对密度函数进行积分得到质量。

同样地，概率密度衡量的是x轴上每个单位的概率。为了得到随机变量落在某个区间的概率^〔1〕，我们可以计算其密度函数在这段区间上的积分。假设随机变量X的概率密度函数为PDF_X，那么X落在区间[-0.5, 0.5)的概率为：

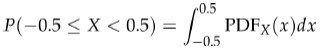
^〔1〕我们可以解释得更具体一些，分布的均值是质心，方差是转动惯量。

因为累积分布函数是概率密度函数的积分，所以上式也可以写成：

P(-0.5≤X<0.5) = CDF_X(0.5)-CDF_X(-0.5)

对有些分布，我们能够得到累积分布函数的解析表达式，这时可以采用第二种表达方式。对于一些无法得到累积分布函数解析表达式的分布，可以用数值积分的方法来计算X在某个区间上的概率。

习题6-5

假设一个随机变量X服从参数为λ的指数分布，那么X落在区间[1, 20]的概率是多少？请将结果表示成一个关于λ的函数，并保留推导结果，我们将在8.8节用到。

习题6-6

从BRFSS（见4.5节）的数据中，我们发现人类身高大致服从正态分布，男性身高的均值为178 cm、方差为59.4 cm；女性身高的均值为163 cm、方差为52.8 cm。

蓝人乐团要求成员为男性，身高介于178 cm和185 cm之间，那么在美国男性中身高介于该区间的人有多少？