6.2　关联性

一想到数据的关系，人们的脑子里最先蹦出的概念可能就是关联性，之后便是因果关系。此刻你可能正在琢磨关联性和因果关系到底有什么差别。关联性意味着当一件事情变化时，另一件事情也可能会发生某种变化。比如说，每加仑牛奶的价格和每加仑汽油的价格就是正相关的（positively correlated）。它们都在逐年上升。

下面是关联性和因果关系之间的区别。如果你提升了汽油价格，牛奶价格是否会自动上升呢？更重要的是，如果牛奶的价格确实上升了，真的是汽油价格提升引起的吗？还是有其他外在因素，例如乳制品业突发的罢工行为？

解释所有外在的、混杂的因素无疑非常困难，因此证实因果关系也并非易事。研究人员可能要花费数年的时间来弄清楚这些事情。但是我们可以轻易地发现事物间的关联，而它也一样很有价值。以下各节将会帮助大家理解这一点。

关联性可以帮助我们根据某一已知指标来预测另一指标。要想探究这种关系，让我们看看散点图和多重散点图。

6.2.1　更多的圆点

在第4章中，我们曾用散点图来表示随时间而变化的指标：时间由水平轴表示，数值或量度则在垂直轴上表现。它有利于我们辨识出随时间发生的变化（或者不变化）。这种图表体现的是时间和另一因素或变量之间的关系。其实，散点图不仅可以应用于时间，还可以表现两个变量之间的关系，如图6-1所示。

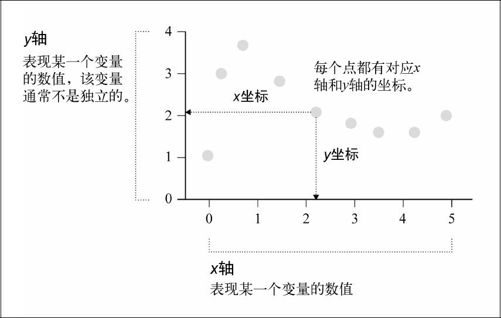
图6-1　散点图的基本框架，比较两个变量

如果两个指标是正相关的（参见图6-2左图），那么从左往右读图表时，点的位置就会越来越高。相反，如果是负相关，那么点的位置就会从左往右越来越低，如图6-2中图所示。

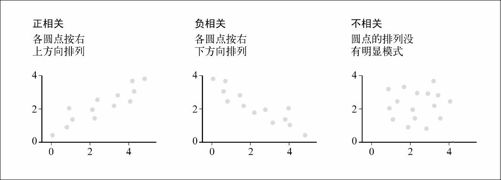
图6-2　散点图中显示的关联性

有时候数据之间的关系非常直接，例如人的身高和体重之间的关联性。通常，一个人的身高增加后体重也会随之增加。还有些时候关联性并没有那么明显，比如健康和体质指数（Body Mass Index，BMI）之间的关系。BMI过高通常意味着某人超重了，但肌肉发达的人（比如运动员）也会有很高的BMI。如果抽样群体是健美运动员或者橄榄球员又会是什么情况？健康和BMI之间有什么关系？

请记住图表只是整个故事的一部分而已。对故事结果的解读仍然取决于人。而这对于关系来说非常重要。也许你会尝试表现出数据间的因果关系，但大多数情况下它们都并不准确。汽油价格和世界人口都在逐年增长，但这并不意味着降低汽油价格，人口增长就会减缓。

创建散点图

在本例中，我们看一下2005年美国各州的犯罪率，即美国人口统计局公布的每10万人口中谋杀、抢劫和故意伤害等罪案的发生率。总共有7种犯罪类型，让我们先来了解其中的两种：入室盗窃和谋杀。这两者之间是否存在联系？是否在谋杀率相对较高的州，入室盗窃也发生得较多？让我们用R来进行调查。

和之前一样，第一件事就是在R中利用read.csv( )来载入数据。你可以访问http://datasets.flowingdata.com/crimeRatesByState2005.csv下载CSV文件，不过这里我们直接通过URL读取。

# 输入数据
crime <-
    read.csv('http://datasets.flowingdata.com/crimeRatesByState2005.csv',
    sep=",", header=TRUE)

现在检查一下头几行数据，输入变量crime，之后设置你希望看到的行数。

crime[1:3,]

以下是R返回的前几行数据。

          state murder forcible_rape robbery aggravated_assault burglary
1 United States    5.6          31.7   140.7             291.1    726.7
2       Alabama    8.2          34.3   141.4             247.8    953.8
3        Alaska    4.8          81.1    80.9             465.1    622.5
  larceny_theft motor_vehicle_theft population
1        2286.3               416.7  295753151
2        2650.0               288.3    4545049
3        2599.1               391.0    669488

第一列显示的是州名，其他列是各种类型犯罪的发生率。比如说，2005年美国全国的平均抢劫案发生率是每10万人口中发生140.7起。我们用plot( )来为谋杀和入室盗窃两个数据创建默认的散点图，结果如图6-3所示。

图6-3　默认生成的有关谋杀案和入室盗窃案的散点图

plot(crime$murder, crime$burglary)

看上去这两个数据似乎是正相关的：谋杀率相对较高的州，其入室盗窃率也相对较高。但由于有一个点出现在很远的最右侧，所以这个关系并不是很容易发现。这个点（也就是离群值）导致水平轴必须延伸得很长。它代表的是华盛顿特区，该地区的谋杀率远高于其他地区，达到了35.4。谋杀率第二高的州是路易斯安那和马里兰，为9.9。

为了让图表更加清楚，带来更大的帮助，我们可以拿掉华盛顿特区，同时去掉全美平均值，聚焦于各个单独的州。

crime2 <- crime[crime$state != "District of Columbia",]
crime2 <- crime2[crime2$state != "United States",]

第一行在crime2中存储了华盛顿特区以外的数据。与之类似，第二行过滤掉了全美平均值。

现在再次绘制得到的图表会更加清晰，如图6-4所示。

图6-4　过滤掉数据之后的散点图

plot(crime2$murder, crime2$burglary)

如果让轴从0开始可能会更好，所以在这里再进行一些设置。x轴应该从0到10，y轴应该从0到1200。这样做会把所有点的位置向右上移动，结果如图6-5所示。

plot(crime2$murder, crime2$burglary, xlim=c(0,10), ylim=c(0, 1200))

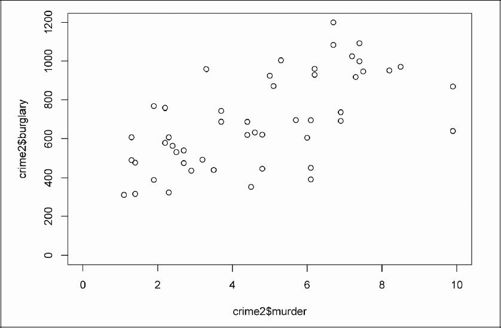
图6-5　坐标轴从0开始的散点图

你知道什么能够让这个图表更加有用吗？自然是第4章中提到的LOESS曲线。它能帮助我们更加明确地观察入室盗窃率和谋杀率之间的关系。通过scatter.smooth( )来绘制各点间的曲线，结果如图6-6所示。

scatter.smooth(crime2$murder, crime2$burglary,
    xlim=c(0,10), ylim=c(0, 1200))

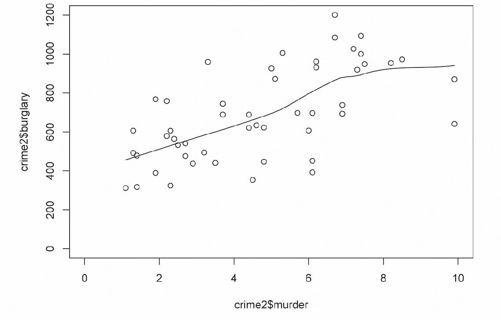
图6-6　运用曲线来估算关系

说明　为了简化起见，华盛顿特区被从数据集中移走了，这样便于我们更好地观察其他数据。但是数据中的这些离群值其实是很重要的。我们将会在第7章中继续讨论这一问题。

作为一个基础图表，这样已经很不错了。如果你只是为了方便分析，到底就算大功告成。但如果这份图表还会有其他读者，你也可以稍微作一些修改，改善它的可读性，如图6-7所示。

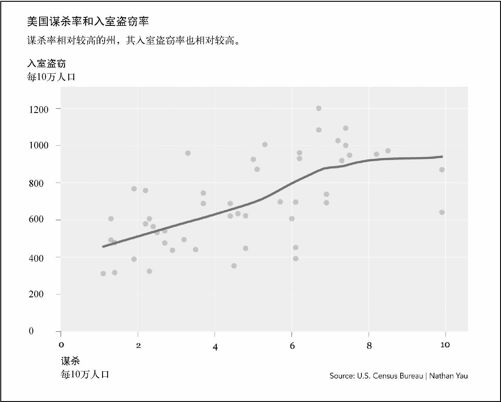
图6-7　改进后的谋杀案和入室盗窃案发生率散点图

我去掉了厚重的边框，削弱了四周的框架感，并加粗了曲线、将点的颜色调暗，从而将读者的注意力吸引到曲线上面。

6.2.2　探索更多的变量

现在我们已经针对两个变量进行了比较和绘制，下一步自然是比较其他变量。当然，你也可以总是只挑选两个变量，然后绘制它们的散点图，但这样一来很可能会丢掉很多机会，无法体现出数据中其他有意思的地方。这是我们所不希望看到的。所以最好是用散点图矩阵的形式，绘制出每一种可能的配对，如图6-8所示。

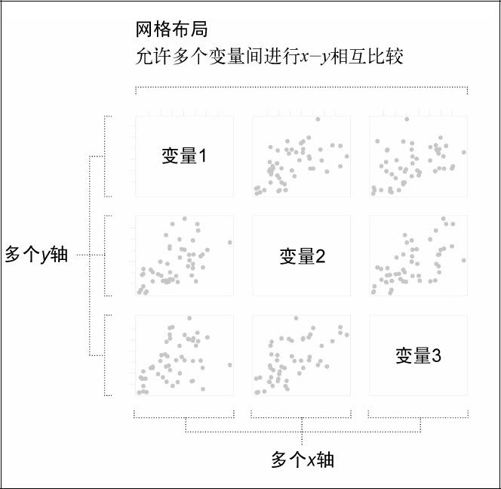
图6-8　散点图矩阵的基本框架

这种方法在数据探索阶段特别有用。也许在你面前有一堆数据集，但你对从哪开始却没有任何头绪。如果你自己都不太清楚数据中蕴涵的意义，那么你的读者就难理解了。

提示　必须理解自己的数据才能讲述一个完整的故事。你对数据了解得越透彻，所讲的故事就会越精彩。

散点图矩阵能够满足我们的期望。它通常是一个方格网，在垂直和水平方向上都列出了所有的变量。水平轴上的每一列都代表一个变量，垂直轴上的每一行也代表一个变量。这样就提供了所有可能的配对，而对角线则可以空出来放置标签，因为不用拿变量与其自身进行比较。

创建散点图矩阵

现在让我们回到犯罪率数据。我们有7个变量，或者说7个类型的犯罪率，但在之前的例子中我们只比较了其中的两个：谋杀案和入室盗窃案。而通过散点图矩阵，我们可以比较所有的犯罪类型。图6-9显示了最终的效果。

图6-9　美国各州犯罪率的散点图矩阵

和我们预料的一样，有很多都是正相关。比如说入室盗窃和故意伤害的关联性就比较高。前者增加时后者也会随之增加，反之亦然。不过，谋杀和扒窃之间的关系就不是这么显而易见了。因此你不能轻易作出任何假设，而散点图矩阵的价值就体现在这里。有可能第一眼看上去你会感觉这些线条和图表很容易混淆，但从左到右、从上到下地阅读它，无疑会得到很多信息。

很幸运，在R中创建散点图矩阵和创建单个的散点图一样容易。仍然还是利用plot( )函数，不过这次不止传递两个列，而是整块数据，只不过减去第一列，因为它的内容是各个州名。

plot(crime2[,2:9])

这行代码能生成图6-10中显示的矩阵，和我们想要的已经不远了。不过要想帮助读者更容易地辨识数据间的关系，还应该加上拟合曲线。

图6-10　R默认生成的散点图矩阵

要想创建带有拟合LOESS曲线的散点图矩阵，我们可以转而使用pairs( )函数，其实也非常简单。结果如图6-11所示。

pairs(crime2[,2:9], panel=panel.smooth)

图6-11　带有LOESS曲线的散点图矩阵

提示　pairs( )中的panel参数调用了一个有关x和y值的函数，本例中也就是panel.smooth( )。它是R中的一个原生函数，用于生成LOESS曲线。当然你也可以指定自己的函数。

现在我们已经有了一个很好的基础框架了，之后的工作就是让它提高可读性（参见图6-9的最终效果）。将图表存为PDF格式，然后在Illustrator里打开。

大体上来讲，我们需要削弱杂乱感，让重要的内容得到强调。犯罪类型和趋势曲线的重要性是第一位的，各个圆点其次，坐标轴最后，因此在颜色和大小上也应该按此轻重顺序进行调整。对于对角线上的标签，可以适当增加文字的大小，并用灰色填充方框，让它们凸显出来。然后加粗各条趋势曲线，调整它们的颜色，加大线与点之间的反差。最后减小边框和网格线的粗细，并改为浅灰色，使之得以弱化。对比图6-9和图6-11，很明显前者的表现力要更强一些，是不是？

提示　明确你要讲述的故事的重点，然后在图表设计中有意强化这些地方。但请注意不要扭曲事实。

6.2.3　气泡

自从卡罗琳学院的国际卫生学教授、Gapminder基金会理事Hans Rosling用他的动态图表来演示有关国家贫富和健康的故事以来，在x-y轴上按比例显示的气泡就为世人所熟知，而且受到了极大的欢迎。虽然他的动态图表通过动画来展现随时间发生的变化，但我们一样可以创建它的静态版本：气泡图。

►访问Gapminder网站www.gapminder.org欣赏Hans Rosling的著名演讲，其中包括BBC出品的纪录片The Joy of Stats，该片讲述了统计学的无穷乐趣。

最简单的气泡图就是一系列尺寸按比例显示的气泡，不过现在我们可以考虑它的变体，也就是带有“气泡”维度的散点图。

这种图表类型的优势在于它便于我们一次比较3个变量，如图6-12所示。一个变量是x轴，一个变量是y轴，而第三个则通过气泡的面积大小来体现。

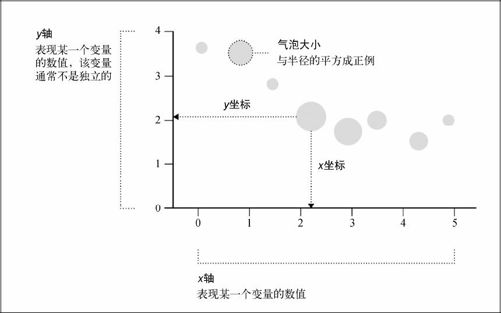
图6-12　气泡图的基本框架

需要注意的是气泡的面积大小，因为很多人会在这个地方出错。在第1章中我们就曾提到过，气泡的大小是根据面积来的，而不是半径、直径或者圆的周长。如果马虎地按软件默认选项进行绘制，最后得到的圆形就很可能不是过大就是过小。

提示　在用圆形表示数据时，要根据圆的面积来定义尺寸，而不是半径、直径或者周长。

我们举一个简单的例子来说明。假设你负责公司的广告销售，现在正在测试网站上的两个banner广告，以便了解哪一个广告的宣传效果更好。这两个广告都投放了一个月的时间，但获得的点击次数是不同的：第一个banner被点击了150次，而第二个banner只被点击了100次。因此，第一个banner的效果比第二个要好50％。图6-13中根据圆形的面积表现了两个banner气泡的大小关系，其中第一个圆比第二个要大50％。

图6-13　通过面积对比的两个气泡

而在图6-14中则是根据半径的长短来表现两个气泡的大小关系。

图6-14　通过半径对比的两个气泡

第一个圆的半径比第二个圆的半径要长50％，这使得第一个圆的面积超过了第二个图的2倍还要多。虽然看上去这还不算什么大问题（现在只有两个数据点，比较起来还算容易），但在尝试表现更多数据时，这一问题就会很容易造成困扰。

创建气泡图

让我们看一下将要实现的最终图表效果，如图6-15所示。它依然是有关美国各州谋杀案和入室盗窃案的数据，但加入了各州的人口数量作为第三维度。是否人数越多的州，犯罪率也会越高？事实上并没有这么单纯（和大多数情况一样）。像加利福尼亚、佛罗里达和得克萨斯这些大州确实很接近象限的右上部分，而纽约州和宾夕法尼亚州的入室盗窃率却相对较低。与之类似，路易斯安那和马里兰的人口较少，但却位于图表的最右边。

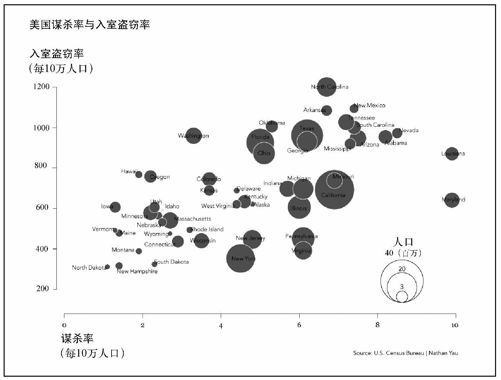
图6-15　显示美国犯罪率的气泡图

首先在R中用read.csv( )载入数据。这次的数据和我们之前所使用的基本上相同，只不过加入了一列人口数量，而华盛顿特区被移除了。另外它不是通过逗号分隔，而是制表符分隔。不过这没什么大不了的，只需在函数内稍微改动一下sep参数即可。

crime <-
    read.csv("http://datasets.flowingdata.com/crimeRatesByState2005.tsv",
    header=TRUE, sep="\t")

之后就可以直接用symbols( )函数来绘制气泡了。x轴是谋杀率，y轴是入室盗窃率，而气泡的半径是根据人口数量计算得出的。结果如图6-16所示。想尝试一下symbols( )的其他功能吗？在后文中马上就会看到。

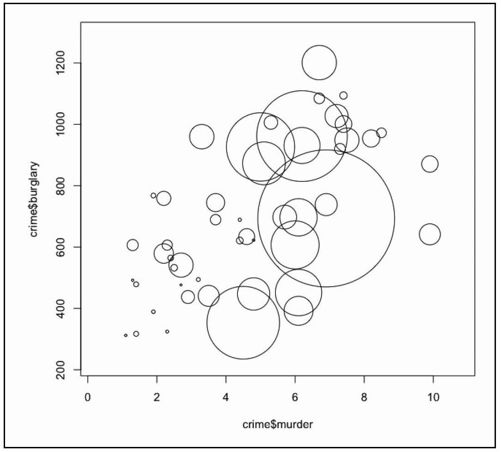
图6-16　默认生成的气泡图

symbols(crime$murder, crime$burglary, circles=crime$population)

搞定，对吧？错，这是用来考验你的。这些圆的大小是根据人口比例换算成半径来定义的，而我们需要的是根据面积来定义。因为如果按半径来指定的话，相互之间的比例就会紊乱。加利福尼亚州的人口（由中间那个巨大的圆形代表）真的比其他州要多出那么多吗？

要想正确地定义大小，先来看一下圆面积的计算公式。

代表人口数量的是每一个气泡的面积。我们需要弄明白怎样通过半径来定义大小，所以把半径移到等号左侧可以发现，它应该是和面积的平方根成正比例的。

你可以直接去掉π,因为它只是一个常量，不过为了清楚起见，还是把它留在那里。现在就不能只通过rime$population来指定圆的半径了，而应该计算出它的平方根，然后插入到symbols( )里面。

radius <- sqrt( crime$population/ pi )
symbols(crime$murder, crime$burglary, circles=radius)

第一行代码创建了一个平方根取值的新向量，并存储到radius中。图6-17显示了正确大小的气泡图，但显得比较杂乱，因为那些人口少于加利福尼亚的州的气泡都变大了。

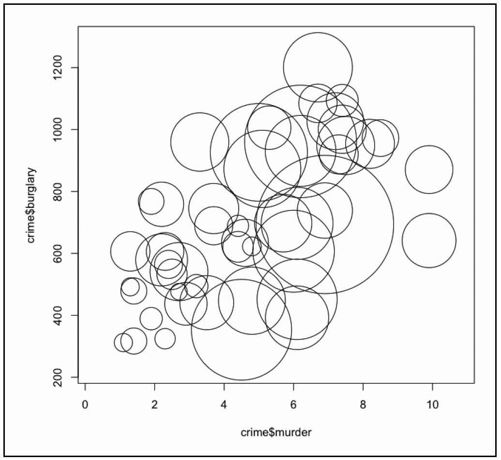
图6-17　默认生成的正确尺寸的气泡图

我们需要把所有的圆都按比例缩小才能看清楚图表的内容。symbols( )中的inches参数可以设定最大圆形的大小，单位是英寸。默认的大小是1英寸，所以在图6-17中加利福尼亚州气泡的大小就是1英寸，其他的气泡都据此按比例缩小。我们可以缩小最大的气泡（比如说0.35英寸），但比例保持不变。此外还可以通过fg和bg参数来改变每个圆的边框和填充色，并且为坐标轴加上你自己的标签。图6-18显示了最终的输出结果。

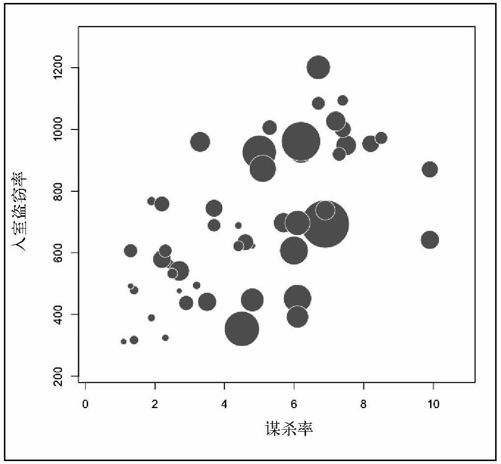
图6-18　气泡缩小后的气泡图（另见彩插图6-18）

symbols(crime$murder, crime$burglary, circles=radius, inches=0.35,
    fg="white", bg="red", xlab="Murder Rate", ylab="Burglary Rate")

现在的效果有点感觉了。

你也可以通过symbols( )用其他形状来创建图表，例如正方形、矩形、量度表、箱形图和星形图。它们的参数和使用圆形时稍有不同。比如说正方形，就是用它的边长来定义大小。不过和气泡一样，我们需要用面积来表现各个正方形之间的关系，换句话说，需要通过面积的平方根来指定正方形的边长。

图6-19显示了使用正方形后图表的样子。代码如下：

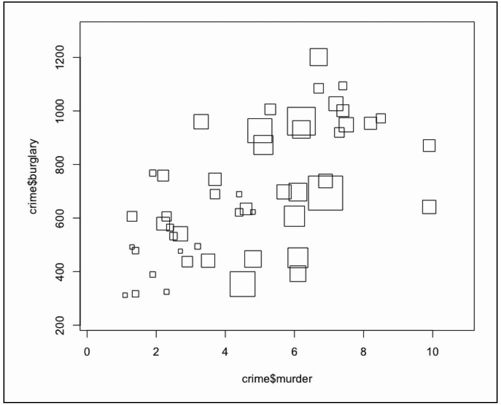
图6-19　用正方形代替圆形

symbols(crime$murder, crime$burglary,
    squares=sqrt(crime$population), inches=0.5)

现在还是让我们回到圆形。图6-18中的图表已经有了分布的感觉，但是读者还是不知道哪个圆代表哪个州。所以我们还需要添加标签。这会用到text( )函数，它的参数包括x轴坐标、y轴坐标和具体显示的文字内容，这些我们手上都有。和代表各州的各个气泡一样，各州名的x轴坐标来自于各州的谋杀率，y轴坐标来自于各州的入室盗窃率。具体显示的文字则是各州的名称，来自于我们的原始数据块中的第一列。

text(crime$murder, crime$burglary, crime$state, cex=0.5)

其中cex参数控制的是文本的大小，默认值为1。如果取值大于1，标签就会更大，反之则会更小。标签默认是以x轴和y轴坐标居中对齐的，如图6-20所示。

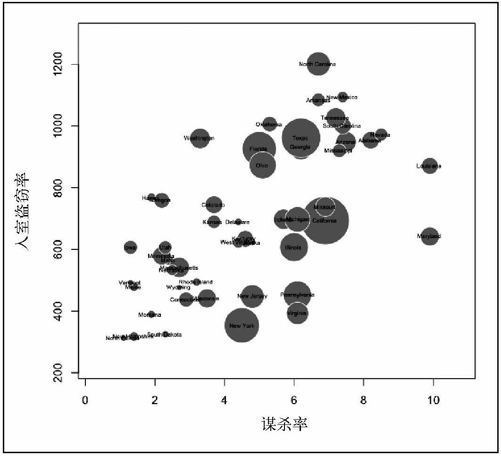
图6-20　带有标签的气泡图

到了这一步，已经很接近图6-15所示的最终效果了。将R中生成的图表另存为PDF格式，然后用你自己擅长的绘图软件进行调整，把它改成你希望的样子。你可以对图表进行简化，比如让坐标轴变得更细，并且删除四周的边框。你也可以调整某些标签的位置，尤其是位于左下角的那几个州，以便读者辨识出它们的名字。此外需要把乔治亚州的气泡挪到上方，因为它被面积更大的得克萨斯州给挡住了。

这就是气泡图。在R中输入?symbols可以了解更多绘图选项。不妨大胆一点，多试试。