6.3　分布

大家也许听说过平均数（mean）、中位数（median）和众数（mode）。美国一般会在高中教这些东西，不过我觉得这也有点太晚了。平均数指的是将所有数据点相加然后除以数据点的个数。中位数指的是将所有数据按从小到大依次排列，然后找到位于最中间的那个数据点。众数则是指在所有数据点中出现频率最高的那个数字。这些数字都有其价值，也很容易得出，但是它们仅仅描述了数据大概的分布情况，无法展现出故事的全貌。而用可视化的方式来表现所有的内容，其中的分布自然也就一目了然了。

图表的重心如果向左偏斜，则表明大部分数据都聚集在整个取值域较低的一端。向右偏斜则含义相反。平坦的线意味着均匀分布，而经典的钟形曲线则表明大部分数据聚集在平均值附近，同时向两端逐渐减少。

接下来会先向大家介绍一种经典的图表类型，让你对分布有一个更直观的认识，之后我们将讨论更加实用的直方图（histogram）和密度图（density plot）。

6.3.1　老式的分布图表

在20世纪70年代，计算机还远未普及，绝大部分的数据图表都是手绘的。著名的统计学家John Tukey就在他的著作《探索性数据分析理论》（Exploratory Data Analysis）中给出了一些建议，基本上都是关于如何用钢笔和铅笔来区分线条和色彩的明暗度。你也可以用各种花纹作为填充，从而对变量进行区分。

茎叶图（stem-and-leaf plot，或者stemplot）就是在这种环境下被创造出来的。绘制者所要做的就是按照某种顺序来填写数字，最终得到的结果可以让读者对数据的分布有个大致的了解。这一方法在20世纪80年代非常流行（当时在分析中运用统计图表的势头开始增强），因为它制作简单，而且就算是用打字机也能营造出图形感。

虽然说在今天我们有其他更简单、更快捷的方式可以观察分布，但回顾一下这种方式仍然很有价值，因为在制作茎叶图时用到的原则也同样适用于直方图。

创建茎叶图

如果你想回归自然，可以用钢笔在纸上绘制茎叶图。不过用R会快得多。图6-21显示了2008年全球出生率的茎叶图，数据来自于世界银行。

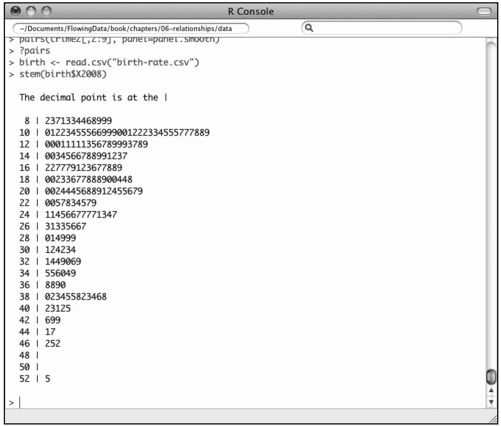
图6-21　显示全球出生率的茎叶图

如你所见，它非常基础。基础性的数字位于左侧（茎），与其相关的数字依次排列在右侧（叶）。在本例中，竖线（|）表示小数点，左侧代表整数，右侧代表各数据的小数位第一个数字。所以在2008年，世界各国每1千人口中的出生率最常见的区间是10到12之间。不难看出，有一个国家（尼日尔）的出生率最高，在52到54之间。

以下是手绘茎叶图的方法。从8开始写下数字，以52结束，其中以2为间隔，按从上到下排列。在这一列数字的右侧画一条竖线，然后逐行检查2008年的各国数据，并相应在竖线的右侧添加各数据小数点后的第一个数字（如果有多个数字，则四舍五入）。比如说，某个国家的出生率是8.2，那么就在数字8的右侧添加一个数字2。如果有一个国家的出生率是9.9，它依然也会归于数字8那一行，我们就应该在后面接着添加一个数字9。

很明显，如果数据很多，这个过程就会相当吃力。因此我们来看看怎样在R中绘制茎叶图。在载入数据之后，只需调用stem( )函数即可。

birth <- read.csv("http://datasets.flowingdata.com/birth-rate.csv")
stem(birth$X2008)

这就完成了。如果你想让它更美观一点，比如说像图6-22那样，那么可以复制R中的文本，然后粘贴到其他地方调整样式。不过这种方法已经过时了，用直方图可能会好很多。其实直方图基本上就是更加图形化的茎叶图。

图6-22　稍加改进后的茎叶图

6.3.2　有关分布的柱形

观察图6-22中的茎叶图，我们可以辨识出每个具体取值域各自的出现频率。某个出生率取值域内的国家越多，绘制出的数字就越多，因此所处的那一行也会越长。现在逆时针翻转茎叶图，让它的行变成列，可以发现越高的列表示该取值域内的国家越多。现在把每一列的数字改成简单的柱形（或者说矩形），我们就得到了一个直方图，如图6-23所示。

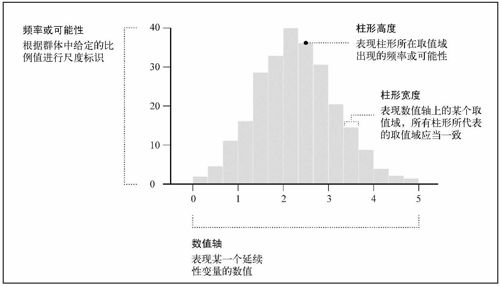
图6-23　直方图的基本框架

柱形的高度表示频率，而柱形宽度没有具体意义。直方图的水平轴和垂直轴都是连续的，而一般柱形图的水平轴上各个数值则是相互分离的。在使用柱形图时，一般会通过水平轴表现各种类别，而且各个柱形之间通常会留有间隙。

有许多人不像我们这样长期与数据图表打交道，他们往往会误认为水平轴只能是时间。水平轴可以是时间，但绝不仅限于此。在考虑我们的受众群体时这一点非常重要。如果你的图表主要呈现给普通读者，那么就需要解释图表的阅读方法，以及他们需要注意的地方。另外要记住，仍然有很多人并不熟悉分布的概念，所以在设计图表时一定要清晰，并且尽量设身处地地帮助读者。

创建直方图

和茎叶图一样，用R创建直方图也非常容易。利用hist( )函数再次绘制全球出生率的分布图，结果如图6-24所示。注意到它的形状与图6-22的茎叶图之间的相似之处了吗？

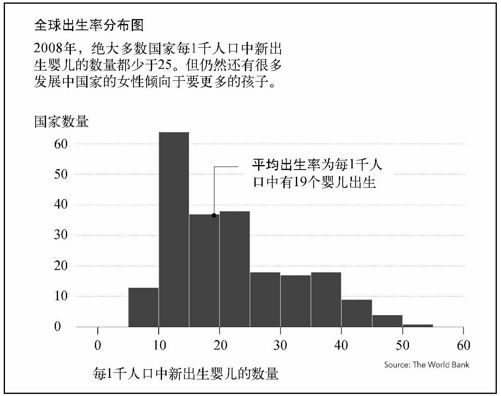
图6-24　全球出生率分布图

假设你在之前的例子中已经载入了数据，那么现在可以直接用hist( )函数来处理2008年的数据了。

hist(birth$X2008)

图6-25显示了默认生成的直方图。

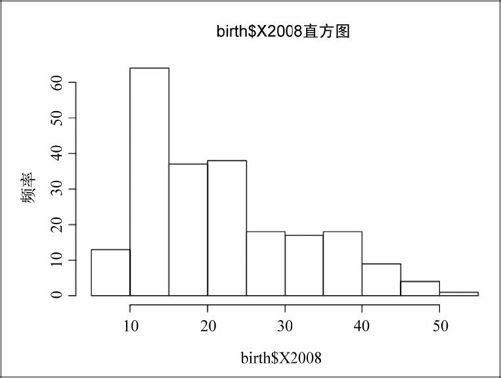
图6-25　默认生成的直方图

在默认生成的直方图中有10个柱形（或者说取值域），但我们可以通过breaks参数随心所欲地修改。比如说可以设置得到如图6-26所示的更少、更宽的柱形。它只分成了5段。

hist(birth$X2008, breaks=5)

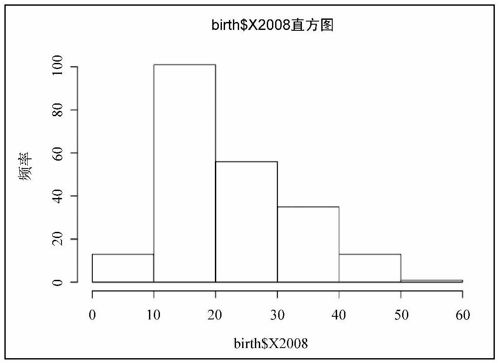
图6-26　分成5段的直方图

我们也可以反其道而行之，让直方图显示更多较窄的柱形，比如说20个（参见图6-27）。

hist(birth$X2008, breaks=20)

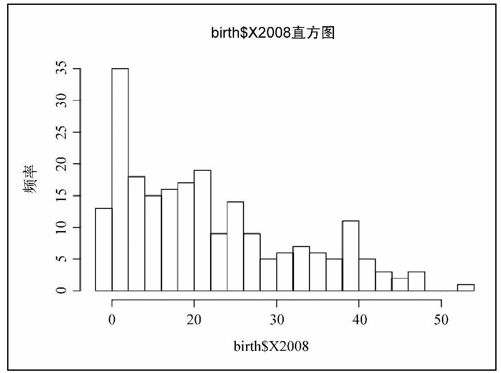
图6-27　分成20段的直方图

你应该根据所要可视化的数据特点来决定分段的数量。如果大部分数据都聚集在某个取值域内，那么就应该采用较多的分段，以便观察其中的细节变化，而不是只生成一个很高的柱形。但如果没有那么多数据，或者数字的分布比较平均，那么较粗的柱形就会更加合适。好消息是如果想试验各种不同数量的柱形，在操作上没有任何难度。

提示　默认的直方图分段数量并不一定就是最佳选择。不断调整参数，选择最适合数据特点的分段数量。

对于出生率数据来说，默认的分段数量还算合理。我们可以看到有一些国家每1千人口中新生婴儿的数量在10以下，但绝大多数国家的这一数字都位于10到25之间。还有不少国家超过了25，但总体数量要少于25以下的国家。

现在可以将图表另存为PDF格式，并在Illustrator中继续编辑。大部分操作都和我们在第4章中针对柱形图所做的类似，不过也可以加入一些直方图特定的内容，从而提高它的可读性。另外最好向读者作一些解释说明。

提示　利用R的summary( )函数，我们可以轻松获取平均数、中位数、最大值、四分位数等关键数字。

在图6-24的最终图表中，你可以看到分布的一些关键点，比如平均值、最大值和最小值等。当然，文字说明也是一个提供解释说明的好机会。此外加入一点颜色会好很多，这样直方图看起来就不那么像线框了。

6.3.3　延续性的密度

虽然直方图的数值轴是延续性的，但整个分布依然被分成了数个柱形。每一个柱形代表的都是一些条目（在上例中也就是国家）的集合。那么在每个柱形内部的变化又是怎样的呢？在茎叶图中，我们确实可以看到每个国家的具体数字，但要想就此估计各国间差距的大小，依然不够直观。其实和第4章中用LOESS曲线来观察趋势一样，我们也可以用密度图来对分布的细节变化进行可视化。

图6-28显示了用曲线代替柱形图的效果。曲线以下的总面积等于1，垂直轴代表的是可能性，或者说样本群体中某个值所占的比例。

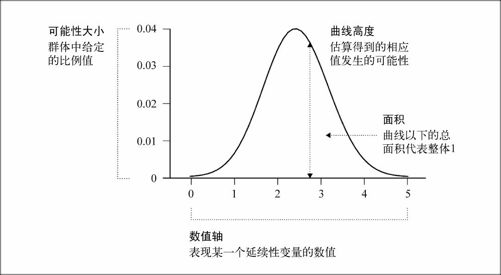
图6-28　密度图的基本框架

创建密度图

让我们回到出生率的数据，要生成密度图还需要一个步骤，不过这个步骤并不复杂。我们需要用density( )函数来估算曲线中的各个数据点，而调用的数据中不能有任何缺失值。在2008年的数据中，有15行都缺失了具体数值（15个国家没有数据）。

在R中，这些缺失值都被标记为NA。幸而我们很容易就能把这些值过滤出去。

birth2008 <- birth$X2008[!is.na(birth$X2008)]

说明　在本例中，为简化起见，我们把缺失值都直接移除了。在你自己探索和可视化数据时，最好多注意一下这些缺失值。它们为什么会缺失？是应该把它们归零呢，还是直接移除？

这行代码会从出生率数据中检索2008年的那一列，然后只读取那些不含有缺失值的行，并存储到变量birth2008中。用技术性语言来描述就是：is.na( )会检测birth$X2008这个向量中的每一个条目，然后通过布尔运算判断各个条目的值是true还是false，最后返回一个长度相同的向量。当我们将这个布尔运算得到的向量传递到原向量的索引中时，就只会返回其中那些值为true的条目了。如果你不太理解这些也没关系，我们无需了解所有的技术细节也一样能够得到结果。不过，如果你打算定义自己的函数，以上内容可能会帮助你了解代码的原理。

现在我们用birth2008储存了“干净”的出生率数据，所以可以将它传递给density( )函数以求出曲线，并将结果存储到d2008中。

d2008 <- density(birth2008)

这行代码可以让我们得到曲线的各个x轴和y轴坐标。我们甚至还可以把这些坐标存储为文本文件，这一点很酷，因为有了这个文本文件，就可以导入到其他的图表绘制软件中去。在R的控制台输入d2008可以看到变量中存储的内容，如下所示：

Call:
    density.default(x = birth2008)
Data: birth2008 (219 obs.); Bandwidth 'bw' = 3.168
    x             y
Min. :-1.299 Min. :6.479e-06
1st Qu.:14.786 1st Qu.:1.433e-03
Median :30.870 Median :1.466e-02
Mean :30.870 Mean :1.553e-02
3rd Qu.:46.954 3rd Qu.:2.646e-02
Max. :63.039 Max. :4.408e-02

我们关心的主要是其中的x和y。以上显示的是各坐标的细目，如果你想获得所有的坐标，可以按以下代码输入：

d2008$x
d2008$y

然后试着用write.table( )将它们保存到文本文件中。该函数中的参数可以指定你希望保存的数据、文件名以及希望使用的分隔符（如逗号或制表符），以及其他一些内容。要想把该数据存为基本的以制表符分隔的文本文件，可以按以下代码输入：

d2008frame <- data.frame(d2008$x, d2008$y)
write.table(d2008frame, "birthdensity.txt", sep="\t")

说明　write.table( )函数会在你当前的工作路径中生成一个新文件。可以通过主菜单或者setwd( )来改变当前的工作路径。

现在你的工作路径中应该出现了一个birthdensity.txt文件。如果你不希望每行都列出序号，或者不希望用制表符而是用逗号作为分隔符，也很容易实现：

write.table(d2008frame, "birthdensity.txt", sep=",", row.names=FALSE)

现在你可以把这些数据导入到Excel、Tableau、Protovis，或者其他任何能识别分隔符文本的软件中去了。几乎所有软件都支持这种格式。

提示　如果你想用R以外的软件来绘图，但又不希望放弃R的计算功能，可以在任何时候通过write.table( )函数来保存当前R中的结果。

让我们回到之前的密度图。我们已经得到了密度图的坐标，现在只需用plot( )函数将它们呈现为图表格式即可。结果如图6-29所示。

plot(d2008)

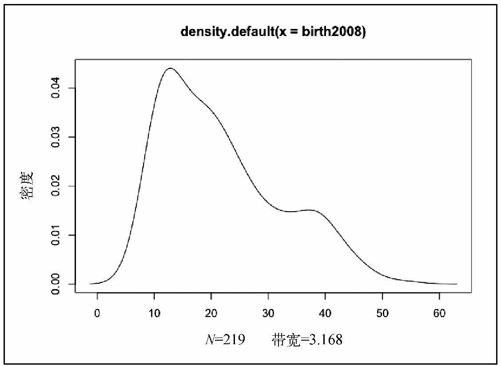
图6-29　出生率的密度图

如果你愿意，也可以通过plot( )加上polygon( )函数创建带有填充色的密度图，效果如图6-30所示。前者用于设置坐标轴，但将type（类型）设为"n"表示暂不绘制。接着用后者来绘制形状，并且将填充色设为暗红色、边框设为浅灰色。

plot(2008, type="n")
polygon(d2008, col="#821122", border="#cccccc")

图6-30　填充后的密度图

现在还可以继续深入一步。可以将直方图和密度图绘制在一起，通过柱形来表现实际频率的分布、通过曲线来表现计算得出的比例，如图6-31所示。这里用到的是histogram( )（来自于lattice工具包）和lines( )这两个函数。前者创建一个新的图表，而后者在已有的图表上加上线条。

library(lattice)
histogram(birth$X2008, breaks=10)
lines(d2008)

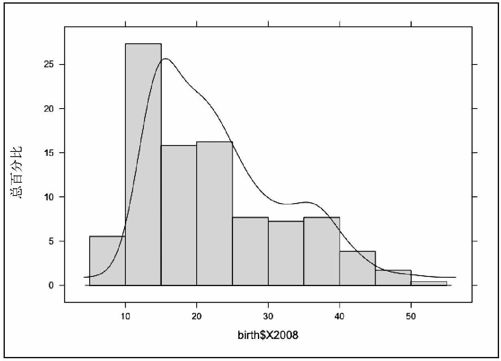
图6-31　直方图和密度图的混合

我们能做的有很多，还可以加入各种变化，但其中涉及的数学和几何学知识其实和老式的茎叶图是一样的，无非是计算、聚合然后分组。我们可以根据数据对象的特点来决定选择何种变体。图6-32显示了经过修饰后的图表。我弱化了坐标轴，重新添加了标签，并标出了平均值。表现密度的垂直轴在本图中的作用不大，不过出于完整性的考虑我依然还是保留了它。

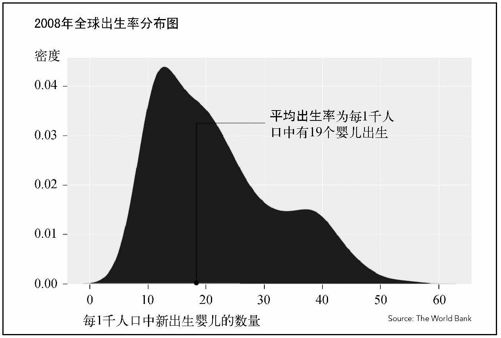
图6-32　2008年全球出生率的密度图