7.3　减少维度

当我们使用切尔诺夫脸谱图或平行坐标图时，主要的目的是去减少。我们希望在数据集或者全体中找出不同的分组。这里的挑战在于，我们并不总是清楚从哪里开始观察这些脸谱或者连接线，所以如果能根据某些标准将对象划分为不同的群集，事情就会容易得多。这就是多维量法（MultiDimensional Scaling, MDS）的目的之一。将所有事物都考虑进来，然后在图表上将相互更类似的对象靠近放置。

这一主题内容极为丰富，专门介绍这一主题的书籍就有很多，因此要具体解释起来恐怕会过于技术化。为了简单起见，我会只停留在概念层面，把背后的算法暂时放在一边。不过话又说回来，多维量法是我在读研时学到的第一个概念，如果你希望深入了解统计学的话，它背后的理论的确值得花时间好好学习。

►有关该方法地更多细节，请查阅多维量法或主成分分析

假设你现在和另两个人在一个正方形的空房间内。你的任务是根据这两个人的身高安排他们站在合适的位置。他们的身高越接近，就应该彼此靠得越近，如果身高相差越远，彼此的距离就应该拉得更大。其中一人很矮，而另一人很高。这两人应该怎么站？他们应该站在相对的角落里，因为他们的身高是截然相反的。

现在又进来了一个人，他的身高中等。根据我们的安排规则，这个新来的应该站在房间的中心，就在之前两个人的正中间。他与高个子的身高差距和矮个子是一样的，因此他和两个人的距离彼此相等。与此同时，高个子和矮个子之间依然保持最大距离。

好，现在再引入另一个变量：体重。你知道所有这三个人的身高和体重。矮个子和中等个子的体重完全相等，而高个子的体重最轻。那么，根据身高和体重，你如何安排这三个人在房间中的位置？如果保持前两个人（矮个子和高个子）的对角位置，那么第三个人（中等个子）就应该向矮个子靠近，因为他们的体重是相同的。

现在你理解我们的安排规则了吗？两个人越相似，他们彼此间的距离就应该越靠近。在这个简单的例子里，你只有3个人和2个变量，很容易人工计算出结果来。但如果有50个人，而且你需要根据5种标准来安排他们在房间里的位置，就会棘手得多。而这就是多维量法的用武之地。

利用多维量法

用实例来理解多维量法会容易得多，所以让我们再次使用之前的教育数据来看看。首先还是在R中载入数据。

education <-
    read.csv("http:datasets.flowingdata.com/education.csv",
    header=TRUE)

别忘了，每个州都有一行，其中包括美国全国平均值和哥伦比亚特区。每个州都有6个变量：阅读、数学和写作科目的SAT成绩，参加SAT考试的毕业生百分比，高中毕业生就业率，以及辍学率。

和刚才那个房间的比喻类似，只不过这次不再是正方形的房间，而是一个图表；不再是一个个的人，而是一个个的州；不再是身高和体重，而是和教育相关的各项指标。我们的目的还是一样：在一个x-y坐标的图表里面放置各个州，使指标相似的州之间的距离比较接近。

第一步：计算出每个州和其他各州之间的距离。用dist( )函数可以做到这一点。我们只需要第2列～第7列，因为第1列是各个州的名称，而且我们都知道它们是不同的。

ed.dis <- dist(education[,2:7])

在R的控制台中输入ed.dis，我们会看到一系列矩阵。每个单元格表现出该州和另一个州之间相距多远（欧几里得像素距离）。比如说，第2行第2列的值就是阿拉巴马州和阿拉斯加州之间的距离。对象在此时并不太重要，重要的是相互之间的差距。

怎样将这个51×51的矩阵变成一幅x-y轴上的图表呢？现在还不行，除非我们为每个州建立一套x-y轴的坐标。这就是cmdscale( )函数的作用。它会把距离矩阵作为输入，然后返回一系列点，这些点之间的差距将和矩阵所指定的保持一致。

ed.mds <- cmdscale(ed.dis)

再次在R的控制台中输入ed.mds，我们就能看到现在每一行数据都有自己的x-y轴坐标了。将这些值存储为变量x和y，然后放到plot( )函数里面，就会看到结果（见图7-27）。

x <- ed.mds[,1]
y <- ed.mds[,2]
plot(x,y)

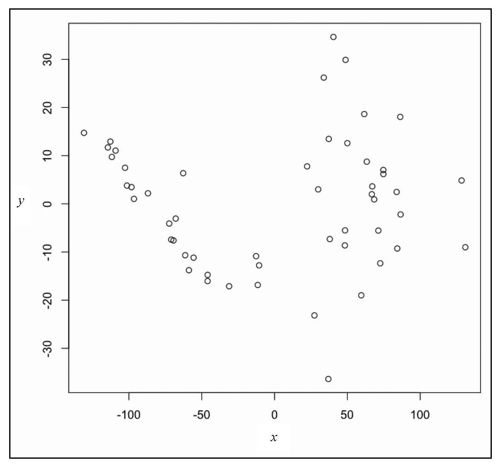
图7-27　显示多维量法结果的点状图

看起来不错。每个圆点都代表一个州。不过还有一个问题：我们不知道哪个点代表哪个州。我们还需要标签，所以跟之前一样，用text（）把州名放在各圆点的位置上，结果如图7-28所示。

plot(x, y, type="n")
text(x, y, labels=education$state)

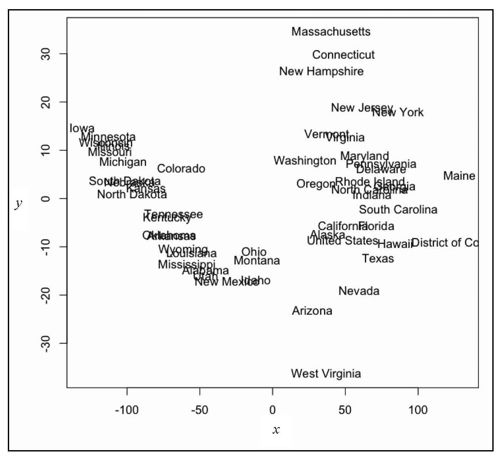
图7-28　用州名来代替圆点，以便观察每个州被放在了什么位置

相当酷。我们能看到图中出现了两个集群，一个在左边，一个在右边。美国（United States）则位于右边集群的底部，略靠中间的位置。到了这一步，你可以自行决定是否继续分析各个集群分别代表什么意思，不过要想开始你的数据探索游戏，这是一个好的起点。

比如说，你可以像之前在平行坐标图里面一样，用dropout_colors来为各个州着色，如图7-29所示。它并不能告诉你太多信息，但确实验证了之前你在图7-25里面看到的内容。

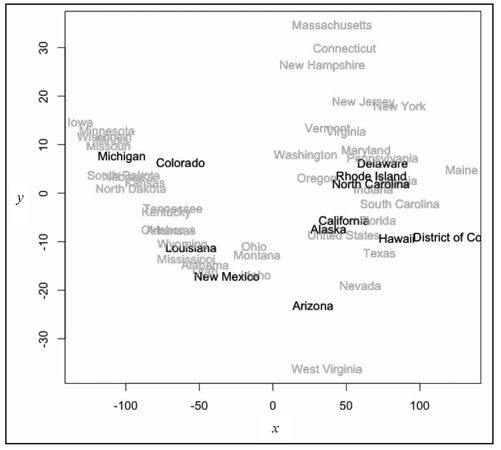
图7-29　按辍学率进行着色的各个州

如果按阅读科目的平均分来着色，结果又会怎样？你当然可以这么做，如图7-30所示。啊，现在似乎已经浮现出清晰的模式了。高分的州都在左边，低分都在右边？是什么让华盛顿州与众不同？仔细看看——稍候你就知道答案了。

图7-30　按阅读科目平均分进行着色的各个州

如果你还想玩点花样，可以尝试一种被称为“基于模型聚类”（model-based clustering）的方法。我不会详细讨论它的细节，只是告诉大家如何实现，并且证明这些并不是魔术，只会涉及数学运算。简要来说，这种方法就是在你的多维量法图表中用mclust工具包来标识出各个集群。如果你还没有mclust工具包，可以安装一个，然后运行下列代码，将得到如图7-31所示的图表。

library(mclust)
ed.mclust <- Mclust(ed.mds)
plot(ed.mclust, data=ed.mds)

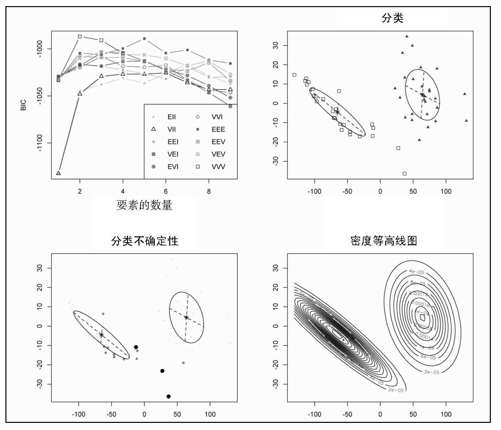
图7-31　基于模型聚类得到的结果

左上角的那幅图表显示了运行算法在数据中找到理想集群数量的结果。其他三幅图表则显示了集群。非常厉害。我们得到了两个集群，现在则更加明确了，显示了高和低的状态。

一般到这个时候，我就该告诉大家将PDF文件导入到Illustrator中进行优化了。不过我不确定自己是否会将这些图表发表给一般读者。对于非专业的读者来说，这些图表过于抽象，很难理解它们的含义。它们对于数据探索来说非常有价值，但我建议还是多使用标准的设计原则为好。找出清楚讲出故事所需要的素材，然后抛掉其他那些。