7.2.2　工作负载

7.2.2　工作负载

1.工作负载的维度

对工作负载的理解和设计可以分为以下几个维度。

（1）密集型计算类型

①CPU密集型计算。

②I/O密集型计算。

③网络密集型计算。

（2）计算范式

①SQL。

②批处理。

③流计算。

④图计算。

⑤机器学习。

（3）计算延迟

①在线计算。

②离线计算。

③实时计算。

（4）应用领域

①搜索引擎。

②社交网络。

③电子商务。

④地理位置服务。

⑤媒体，游戏。

由于互联网领域数据庞大，用户量大，成为大数据问题产生的天然土壤。大数据Benchmark的很多工作负载都是根据互联网领域的典型应用场景产生的。从图7-5中可以看到，BAT三巨头分别规划了自己的互联网布局，涉及电子商务、媒体游戏、社交媒体、搜索门户以及基于地理位置服务等多个领域。每个巨头旗下都有数家小公司与其有着紧密的联系，正是互联网应用中产生了大量的典型大数据工作负载。

由于Spark兴起的时间较Hadoop晚很多，其相应的Benchmark也不如Hadoop可用的多。但是我们也看到，Spark兼容和利用Hadoop存储的数据，这就使用户可以利用以往Hadoop的Benchmark的数据生成器生成数据，使用Hadoop存储数据，然后根据特定的负载重写Spark的工作负载。因为Spark的编程表现力要远远超过Hadoop，所以Hadoop的工作负载完全能用Spark重写，而且Benchmark的负载目的只是突出在特定的计算密集型计算下暴露系统性能瓶颈，一般逻辑简单，所以改写工作量并不大。

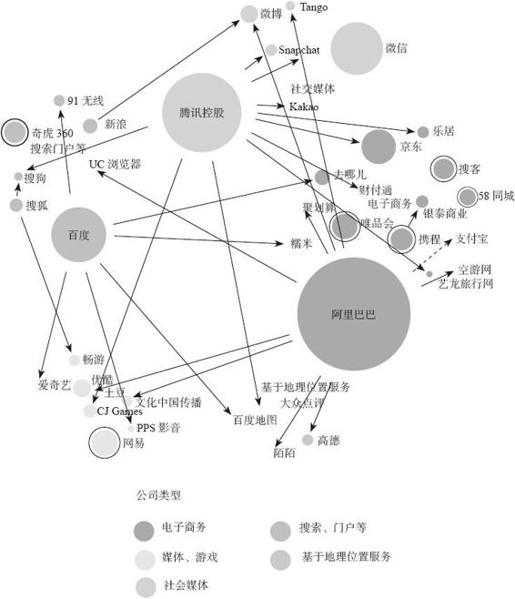
7.2.2　工作负载 - 图1

图7-2　互联网公司业务类型

2.典型的工作负载

下面从计算范式角度介绍典型的大数据工作负载。

（1）基本负载

1）Word Count。

WordCount是CPU密集型的操作负载，WordCount已经在前面有所介绍，在此不再详述。

2）Sort。

排序算法是I/O密集型的负载。

排序算法的实现如下。

object Sort {
 def main（args： Array[String]）： Unit = {
  val host = "Spark：//127.0.0.1：7077"  /*指定Spark的主机地址*/
  var splits = 1    /*读者可以自行设定这里的分区个数*/
  val spark = new SparkContext（host， "Sort"，
   SPARK_HOME， List（JARS））
  val filename = "SortText"
  val save_file = "SortSavedFile"
  val lines = spark.textFile（filename， splits）
  val mapData = lines.map（line => {
   （line， 1）
  }）   /*这里进行映射是为了使用sortByKey的算子，因为sortByKey只能处理key-value pair类型的数据*/
  val result = mapData.sortByKey（）.map{line => line._1}   
  result.saveAsTextFile（save_file）
 }
}

3）Tera Sort

在运行的过程中，map映射和Shuffle阶段是CPU密集型的（CPU intensive），I/O程度中等，在reduce阶段是I/O密集型的（I/O intensive），CPU计算中等。

算法实现思想：当把传统的串行排序算法设计成并行的排序算法时，通常会想到分而治之的策略。排序并行化的一般做法是：把要排序的数据划成M个数据块（可以用Hash的方法做到），然后每个map task对一个数据块进行局部排序，之后，一个reduce task对所有数据进行全排序。这种设计思路可以保证在map阶段并行度很高，但在reduce阶段完全没有并行。为了提高reduce阶段的并行度，TeraSort作业对以上算法进行改进：在map阶段，每个map task都会将数据划分成R个数据块（R为reduce task个数），其中第i（i>0）个数据块的所有数据都会比第i+1个数据块中的数据大；在reduce阶段，第i个reduce task处理（进行排序）所有map task的第i块，这样第i个reduce task产生的结果均会比第i+1个大，最后将1~R个reduce task的排序结果顺序输出，即为最终的排序结果。

（2）机器学习

下面以K-Means聚类算法为例介绍机器学习计算范式

在计算中心点时，K-Means是CPU密集型的计算。在聚类时，K-Means进行I/O密集型运算。

K-Means算法是最为经典的基于划分的聚类方法，是十大经典数据挖掘算法之一。K-Means算法的基本思想是：以空间中k个点为中心进行聚类，对最靠近它们的对象归类。通过迭代的方法，逐次更新各聚类中心点的值，直至得到最好的聚类结果。

假设要把样本集分为c个类别，算法描述如下。

1）适当选择k个类的初始中心。

2）在第n次迭代中，对于任意一个样本，求其到k各中心的距离，将该样本归到距离最短的中心所在的类。

3）利用均值等方法更新该类的中心值。

4）对于所有的k个聚类中心，如果利用2）、3）的迭代法更新后，值保持不变。或者达到指定的迭代次数，则迭代结束，否则继续迭代。

该算法的最大优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。

（3）图计算

下面以PageRank图计算算法为例介绍图计算的计算范式。PageRank广泛用于搜索引擎，对网页图谱进行分析。

1）算法介绍。

PageRank用于衡量特定网页相对于搜索引擎索引中其他网页而言的重要程度，是Google的专有算法。20世纪90年代后期由Larry Page和Sergey Brin开发。PageRank将链接价值概念作为排名因素。

2）算法思想。

一个页面的PageRank由所有链向它的页面（链入页面）的重要性经过递归算法得到。一个页面的权重由所有链向它的页面的重要性决定，到一个页面的超链接相当于为该页投一票。一个有较多链入的页面会有较高的权重，反之，一个页面链入页面越少，权重越低。简而言之，从许多的权重高网页链接过来的网页，必定还是权重高的网页。

PageRank计算基于以下两个基本假设。

·质量假设：指向页面A的入链质量不同，质量高的页面会通过链接向其他页面传递更多的权重。因此，质量越高的页面指向页面A，则页面A也越重要。

·数量假设：若一个页面节点接收到的其他网页指向的入链数量越多，则该页面越重要。

3）算法原理。

初始阶段：网页通过链接关系构建有向图，每个页面设置相同的PageRank值，通过若干轮的迭代计算，得到每个页面最终获得的PageRank值。在每轮迭代中，网页当前的PageRank值不断更新。

迭代：在更新页面PageRank得分的每轮计算中，各页面将其当前的PageRank值平均分配到本页面包含的出链上，每个链接即获得了相应的权值。而每个页面将所有指向本页面的入链所传入的权值进行求和，即可得到新的PageRank得分。且每个页面都获得了更新后的PageRank值时，一轮PageRank计算完成。

（4）计算公式

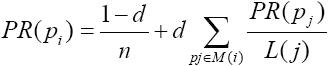
7.2.2　工作负载 - 图2

PR（pi）：pi页面的PageRank值。

N：所有页面的数量。

pi：不同的网页p1、p2、p3。

M（i）：pi链入网页的集合。

L（j）：pj链出网页的数量。

d：阻尼系数，任意时刻，用户到达某页面后并继续向后浏览的概率。

（1-d=0.15）：表示用户停止点击，随机跳到新URL的概率。

取值范围：0＜d≤1，Google设为0.85。

通过链接关系，就构造出了“转移矩阵”。

（5）SQL

结构化查询语言（structured query language，SQL）是一种数据库查询和程序设计语言，用于存取数据以及查询、更新和管理关系数据库系统。SQL可以大致分为以下几个类型：席查询（Ad-hoc query）、报表查询（Reporting query）、迭代查询（Iterative Query）、星型查询（Star query）等，感兴趣的用户可以查看TPC-DS的介绍进行了解。

7.2.2 工作负载