8.4.4　MLlib中的聚类和分类

聚类和分类是机器学习中两个常用的算法，聚类将数据分开为不同的集合，分类预测新数据类别，下面介绍这两类算法。

1.什么是聚类和分类

（1）什么是聚类分析

聚类（Clustering）是指将数据对象分组成为多个类或者簇（Cluster），它的目标是：在同一个簇中的对象之间具有较高的相似度，而不同簇中对象的差别较大。其实，聚类在人们日常生活中是一种常见的行为，即所谓的“物以类聚，人以群分”，其核心思想在于分组，人们不断地改进聚类模式来学习如何区分各个事物和人。

（2）什么是分类分析

数据仓库、数据库或者其他信息库中有许多可以为商业、科研等活动提供决策的知识。分类与预测即是其中的两种数据分析形式，可以用来抽取能够构建分类模型描述重要数据集合或预测未来数据趋势。分类方法（classification）用于预测数据对象的离散类别（categorical Label）；预测方法（prediction）用于预测数据对象的连续取值。

·分类流程：新样本→特征选取→分类→评价。

·训练流程：训练集→特征选取→训练→分类器。

最初，机器学习的分类应用大多都是在这些方法及基于内存基础上所构造的算法。目前，数据挖掘方法都要求具有处理大规模数据集合能力，同时具有可扩展能力。

2.MLlib中的聚类和分类

MLlib目前已经实现了K-Means聚类算法、朴素贝叶斯和决策树分类算法。这里主要介绍广泛使用的K-Means聚类算法和贝叶斯分类算法。

（1）K-Means算法

1）K-Means算法简介。

K-Means聚类算法能轻松地对聚类问题建模。K-Means聚类算法容易理解，并且能在分布式的环境下并行运行。学习K-Means聚类算法，能更容易地理解聚类算法的优缺点，以及其他算法对于特定数据的高效性。

K-Means聚类算法中的K是聚类的数目，在算法中会强制要求用户输入。如果将新闻聚类成诸如政治、经济、文化等大类，可以选择10~20的数字作为K。因为这种顶级类别的数量是很小的。如果要对这些新闻详细分类，选择50~100的数字也没有问题。K-Means聚类算法主要分为3步。第一步是为待聚类的点寻找聚类中心；第二步是计算每个点聚类中心的距离，将每个点聚类到离该点最近的聚类中；第三步是计算聚类中所有点的坐标平均值，并将这个平均值作为新的聚类中心点。反复执行第二步，直到聚类中心不再进行大范围的移动，或者聚类次数达到要求为止。

2）k-Means示例。

表8-7中的例子有7名选手，每名选手有两个类别的比分：A类比分和B类比分。

表8-7　A类和B类比分

8.4.4　MLlib中的聚类和分类 - 图1

这些数据将会聚为两个簇。随机选取1号和4号选手作为簇的中心。1号和4号选手信息如表8-8所示。

表8-8　1号和4号选手信息

8.4.4　MLlib中的聚类和分类 - 图2

第一步将1号和4号选手分别作为两个簇的中心点，下面每一步将选取点和两个簇中心计算欧几里得距离，和哪个中心距离小就放到哪个簇中。表8-9所示为第一聚类。

表8-9　第一步聚类

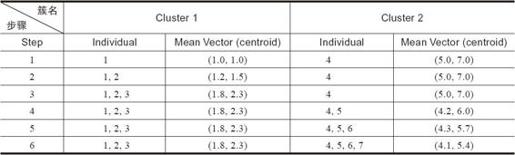
8.4.4　MLlib中的聚类和分类 - 图3

第一轮聚类的结果产生了，如表8-10所示。

表8-10　第一轮结果

8.4.4　MLlib中的聚类和分类 - 图4

第二轮将使用（1.8，2.3）和（4.1，5.4）作为新的簇中心，重复上面的过程，直到迭代次数达到用户设定的次数为止。最后一轮迭代分出的两个簇就是最后的聚类结果。

3）MLlib的KMeans源码解析。

MLlib中的KMeans初始的类簇中心点的选取有两种方法，一种是随机，一种是采用KMeans||（KMeans++的一个变种）。算法的停止条件是迭代次数达到设置的次数，或者在某一次迭代后，所有run的KMeans算法都收敛。

①类簇中心初始化。

MLlib中KMeans初始化方法是对每个运行的KMeans都随机选择K个点作为初始类簇。代码实现如下。

  1. private def initRandom（data： RDD[Array[Double]]）： Array[ClusterCenters] = {
  2.     // Sample all the cluster centers in one pass to avoid repeated scans
  3.     val sample = data.takeSample（true， runs * k， new Random（）.nextInt（））.toSeq
  4.     Array.tabulate（runs）（r => sample.slice（r * k， （r + 1） * k）.toArray）
  5.   }

②计算属于某个类簇的点。

在每一次迭代中，首先计算属于各个类簇的点，然后更新各个类簇的中心。

  1. /* KMeans算法的并行实现通过Spark 的mapPartitions函数获取到分区的迭代器。可以在每个分区内计算该分区内的点属于哪个类簇，之后对于每个运行算法中的每个类簇，计算属于该类簇的点数以及累加和 */
  2.       val totalContribs = data.mapPartitions { points =>
  3.         val runs = activeCenters.length
  4.         val k = activeCenters（0）.length
  5.         val dims = activeCenters（0）（0）.length
  6.         val sums = Array.fill（runs， k）（new DoubleMatrix（dims））
  7.         val counts = Array.fill（runs， k）（0L）
  8.         for （point <- points； （centers， runIndex） <- activeCenters.zipWithIndex） {
  9.           /*找到距离该点最近的类簇中心点 */
  10.           val （bestCenter， cost） = KMeans.findClosest（centers， point）
  11.           /*统计该运行算法开销， 用于在之后选取开销最小的运行的算法 */
  12.           costAccums（runIndex） += cost
  13.           /*将该点加到最近的类簇的统计总和中，方便之后计算该类簇的新中心点 */
  14.           sums（runIndex）（bestCenter）.addi（new DoubleMatrix（point））
  15.          /*将距离该点最近的类簇的点数加1，sum.divi（count）就是类簇的新中心 */
  16.           counts（runIndex）（bestCenter） += 1
  17.        }
  18.        val contribs = for （i <- 0 until runs； j <- 0 until k） yield 
  19. {         （（i， j）， （sums（i）（j）， counts（i）（j）））
  20.        }
  21.         contribs.iterator
  22. /*对于每个运行算法的每个类簇，计算属于该类簇的点，并对点个数求和 */
  23. }.reduceByKey（mergeContribs）.collectAsMap（）
  24. /* mergeContribs是一个负责合并的函数。 */
  25.  def mergeContribs（p1： WeightedPoint， p2： WeightedPoint）： WeightedPoint = {
  26.         （p1._1.addi（p2._1）， p1._2 + p2._2）
  27. }

③更新类簇的中心点。

  1. for （（run， i） <- activeRuns.zipWithIndex） {
  2.        var changed = false
  3.        for （j <- 0 until k） {
  4.          val （sum， count） = totalContribs（（i， j））
  5.          if （count ！= 0） {
  6.            /*计算类簇的新中心点 */
  7.            val newCenter = sum.divi（count）.data
  8.            if （MLUtils.squaredDistance（newCenter， centers（run）（j）） > epsilon * 
  9. epsilon） {
  10.            /*此处代码和算法的停止条件有关 */
  11.              changed = true
  12.           }
  13.           centers（run）（j） = newCenter
  14.         }
  15.       }
  16.      /* 如果在某个run的KMeans算法的某轮次迭代中，K个类簇的中心点变化都不超过指定阈值， 则认
  17. 为该KMeans算法收敛 */
  18.      if （！changed） {
  19.       active（run） = false
  20.       logInfo（"Run " + run + " finished in " + （iteration + 1） + " iterations"）
  21.      }
  22.      costs（run） = costAccums（i）.value
  23.    }

④算法停止条件。

算法的停止条件是迭代次数达到设置的次数，或者所有运行的KMeans算法都收敛。

  1. while （iteration < maxIterations && ！activeRuns.isEmpty）

（2）朴素贝叶斯分类

朴素贝叶斯分类算法是贝叶斯分类算法的多个变种之一。朴素是指假设各属性之间是相互独立的。研究发现，在大多数情况下，朴素贝叶斯分类算法（Naive Bayes Classifier）在性能上与决策树（decision tree）、神经网络（netural network）相当。贝叶斯分类算法在大数据集的应用中具有方法简便、准确率高和速度快的优点。但事实上，贝叶斯分类也有其缺点。由于贝叶斯定理假设一个属性值对给定类的影响独立于其他的属性值，因此假设在实际情况经常是不成立的，其分类准确率可能会下降。

朴素贝叶斯分类算法是一种监督学习算法，使用朴素贝叶斯分类算法对文本进行分类主要有两种模型，即多项式模型（multinomial model）和伯努利模型（Bernoulli model）。MLlib使用广泛应用的多项式模型。下面将以实例简单介绍使用多项式模型的朴素贝叶斯分类算法。

在多项式模型中，设某文档d=（t1，t2，…，tk），tk是该文档中出现过的单词，允许重复。

先验概率P（c）=类c下单词总数/整个训练样本的单词总数

类条件概率P（tk|c）=（类c下单词tk在各个文档中出现的次数之和+1）/（类c下单词总数+|V|）

V是训练样本的单词表（即抽取单词，单词出现多次，只算一个），|V|表示训练样本包含多少种单词。P（tk|c）可以看做是单词tk在证明d属于类c上提供了多大的证据，P（c）则可以认为是类别c在整体上占多大比例（有多大可能性）。

给定如下一组分好类的文本训练数据如表8-11所示。

表8-11　文本训练数据

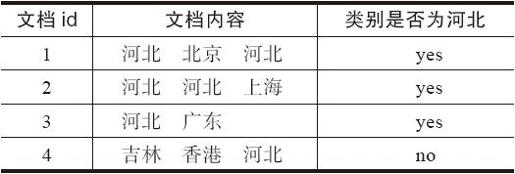
8.4.4　MLlib中的聚类和分类 - 图5

给定一个新样本（河北河北河北吉林香港），对其进行分类。该文本用属性向量表示为d=（河北，河北，河北，吉林，香港），类别集合为Y={yes，no}。

类yes下总共有8个单词，类no下总共有3个单词，训练样本单词总数为11，因此P（yes）=8/11，P（no）=3/11。类条件概率计算如下。

  1. P（河北 | yes）=（5+1）/（8+6）=6/14=3/7
  2. P（河北 | yes）=P（吉林 | yes）=（0+1）/（8+6）=1/14
  3. P（河北 | no）=（1+1）/（3+6）=2/9
  4. P（香港 | no）=P（吉林| no）=（1+1）/（3+6）=2/9

分母中的8是指yes类别下textc的长度，即训练样本的单词总数，6是指训练样本有河北、北京、上海、广东、吉林、香港共6个单词，3是指no类下共有3个单词。所有项中分子中的1和分母中的6代表正则化参数。

有了以上类条件概率，计算后验概率如下。

  1. P（yes | d）=（3/7）3×1/14×1/14×8/11=108/184877≈0.00058417
  2. P（no | d）= （2/9）3×2/9×2/9×3/11=32/216513≈0.00014780

比较大小，即可知道这个文档属于类别“河北”。