8.4.3　数据转换为向量（向量空间模型VSM）

因为机器学习的本质主要是进行矩阵运算，所以在特定的应用领域，需要用户建模，并将领域数据转化为向量或矩阵形式。下面介绍文本处理中的一个常用模型：向量空间模型（VSM）。

向量空间模型将文档映射为一个特征向量V（d）=（t1，ω1（d）；…；tn，ωn（d）），其中ti（i=1，2，…，n）为一列互不雷同的词条项，ωi（d）为ti在d中的权值，一般被定义为ti在d中出现频率tfi（d）的函数，即ωi（d）=ψ（tfi（d））。

在信息检索中，TF-IDF函数ψ-tfi（d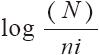）×是常用的词条权值计算方法，其中N为所有文档的数目，ni为含有词条ti的文档数目。TF-IDF公式有很多变种，以下是一个常用的TF-IDF公式。

根据TF-IDF公式，文档集中包含某一词条的文档越多，说明该文档区分文档类别属性的能力越低，其权值越小；另一方面，某一文档中某一词条出现的频率越高，说明该文档区分文档内容属性的能力越强，其权值越大。

可以用其对应的向量之间的夹角余弦来表示两文档之间的相似度，即文档di、dj的相似度可以表示为：

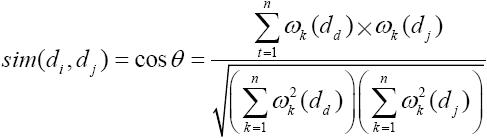
在查询过程中，先将查询条件Q进行向量化，主要依据以下布尔模型。

当ti在查询条件Q中时，将对应的第i坐标置为1，否则置为0，即

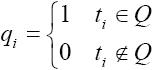
文档d与查询Q的相似度为：

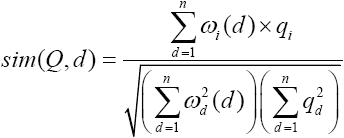
根据文档之间的相似度，结合机器学习的神经网络算法，K-近邻算法和贝叶斯分类算法等一些算法，可将文档集划分为一些小的文档子集。

在查询过程中，可以计算出每个文档与查询的相似度，进而根据相似度的大小，对查询的结果进行排序。

向量空间模型可以实现文档的自动分类，并对查询结果的相似度排序，这能够有效提高检索效率。其缺点是相似度的计算量大，当有新文档加入时，必须重新计算词的权值。