第1章　金券

一个糖果厂老板决定推出一个活动，将五张金券藏到巧克力的包装里，而这种巧克力每年的产量数以千万计。找到金券的人将得到一次珍贵的参观工厂的机会。

如何找到这些金券？你可以买尽可能多的巧克力。你可能会试试用磁铁，可惜金没有磁性。或者你可以雇用数千人，让他们每人筛查一小堆巧克力。这听起来很傻，但是小姑娘维露卡·索尔特就要这么做，因为她特别想得到一张金券，去参观威利·旺卡的巧克力工厂。

维露卡的父亲索尔特先生是个富商，他决定买光他能找到的巧克力。这还不够，就算有堆积如山的巧克力，要从中找到小小的金券也很困难。索尔特先生也有一家工厂，他不惜动用工厂的工人，终于找到了一张金券。他对记者讲述了找到金券的过程：

我是做花生生意的，知道吧，我有大约100个女工为我剥花生，然后将它们做成烤花生米和腌花生米。她们整天就坐在那儿剥花生。所以我跟她们说：“好了姑娘们，不要剥花生了，大家开始给我剥这些破糖纸吧！”然后她们就剥。我让工厂的每一个工人都铆足了劲地撕掉巧克力的包装纸，从早干到晚。

但是三天过去了，我们还是没走运。哦，那可真够呛！我可怜的小维露卡越来越暴躁，每次我一回家她就朝我嚷嚷：“我的金券在哪儿？我要我的金券！”她撒泼又打滚儿，踢腿又叫喊，实在招人烦。我可不希望看到我的小宝贝这么不高兴，所以我决定一直找，不找到她要的东西誓不罢休。终于，在第四天的晚上，一个女工大叫：“我找到金券了！”然后我说：“把它给我，快！”她给了我，然后我跑着回家把它交给了亲爱的维露卡，她高兴得合不拢嘴。我们家又变得其乐融融了。

和索尔特先生一样，无论你打算怎么找那张金券，你都需要大量时间、金钱，或者运气。也许有一天，有人能发明出一个快速找到金券的便宜装置，也许这样的装置并不存在。

然而，1000万对于今天的计算机来说只是很小的数字。如果你把糖果数字化，录入一个数据库，现在的电脑只用不到一秒就能把它找一遍。虽然计算机比人快得多，但它面对的问题的规模也比在糖果里找金券大得多。

现在最大的电子数据集合规模有多大？比如，整个互联网，考虑到所有视频、音频、电子邮件及其他一切，总的信息量差不多有1 000 000 000 000 000 000字节，最多相差几个0。一个字节大致对应键盘上的一个字符。这个数很大，但记住，计算机也很快。一般的笔记本电脑每秒可以执行1万亿次操作，这样算来，理论上只需要不到4个月就能搜完整个互联网的内容，前提是你能把整个互联网装到你电脑的内存里。Google每时每刻都在搜索整个互联网，它使用了几十万台快速的计算机。

如果计算机可以很快地搜遍整个互联网，看起来好像我们就解决了这个找金券问题的电子版。但是，计算机不仅要帮人们搜索已有的数据，还要搜索问题的所有可能解。

认识一下可怜的旅行推销员Mary，她来自华盛顿特区，为美国木槌集团公司工作。她需要从家乡旅行到48个州的首府，向各州法院推销木槌。木槌公司为了削减成本，让Mary找到通过所有城市的最短路径。Mary画了一张图，写写画画了一会儿，制订了一个不错的路线。

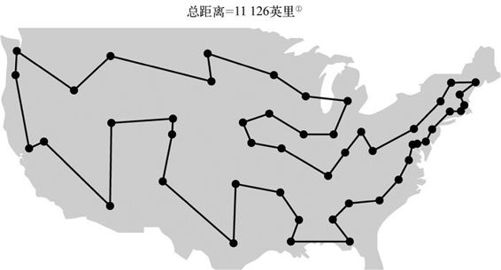
图1-1　旅行推销员问题的地图

^{1 1英里约合1.609千米。——编者注}

差旅部门的人想让Mary试试能否找到另一条路线，把路程缩短到11 000英里以下。Mary写了个计算机程序，试图穷举所有可能的路线，找出最短的一条，但是一周以后，程序还没跑完。Mary坐下来开始算数。作为第一站的城市有48种选择，然后从剩下的47个城市中选一个作为第二站，再从剩下的46个城市中选一个，以此类推。可能的路径共有48×47×46×…×2×1种，也就是下面这个62位数：

12 413 915 592 536 072 670 862 289 047 373 375 038 521 486 354 677 760 000 000 000

即使计算机计算一条路线的时间等于光通过最小的原子直径的时间（大约0.000 000 000 000 000 000 33秒），仍然需要十亿亿亿倍于宇宙年龄的时间才能算完。难怪Mary的电脑算了一周还没有完。Mary想知道有没有比穷举更好的方法找到最佳路线，就像在所有可能行程的“巧克力山”里面刨出那张小小的金券。

这就是本书最基本的问题：P/NP问题。其中的一个实例就是能否为旅行推销员找到最短路径。P和NP自有其十分专业的定义，但是把它们看做概念比看做数学对象更好。NP是存在解的问题的集合，P则是能很快找到解的问题的集合。P=NP意味着我们能总是很快地计算出任何问题的解，当然也包括找到旅行推销员的最短路径。相反，P≠NP意味着我们不能。