3. 大规模数独游戏

数独（Sudoku）是一种起源于日本的填数字游戏，使用一个9×9的格子，如下图所示。

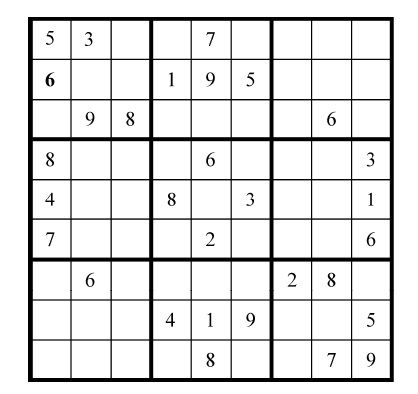
图4-2　数独

数独的游戏目标是填满所有空格，并使每一行、每一列和由黑线标出的3×3小方格中的数字分别是1到9的不重复的数字。

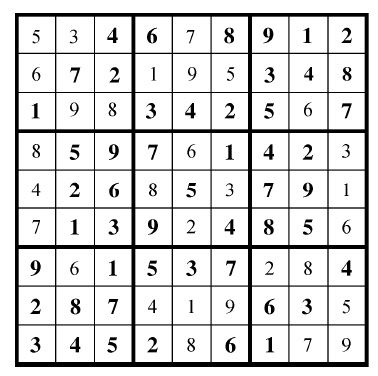
图4-3　数独的解

数独是NP问题，因为很好检查一个解。找到一个解有多难？不太困难。使用简单的回溯算法，普通计算机可以在几秒内找到一个有效解。

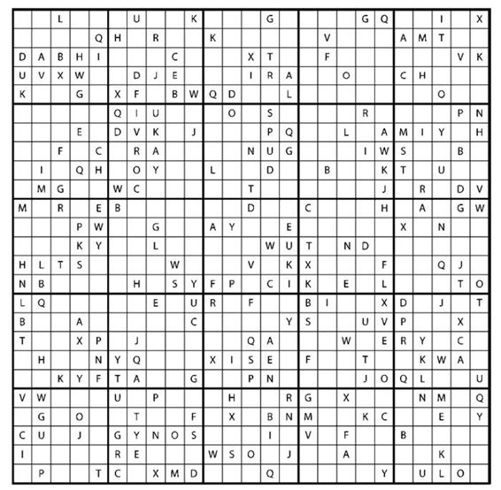
图4-4　大规模的数独

但是如果谜题的规模变得更大，像上面这个25×25的版本，要求每行、每列和小方块中填入A到Y且不重复的字母，会发生什么呢？

这回普通计算机就得算好长时间了，而100×100的数独游戏能打败当今最快的机器。

大规模的数独游戏是NP完全问题。你自认为是数独高手？如果你能可靠地解决大规模的数独，那么你也能解决可满足性问题、旅行推销员问题，还有其他几千个NP完全问题。

数独可不是桌面游戏中唯一一个NP完全问题。来看微软Windows系统自带的扫雷游戏。

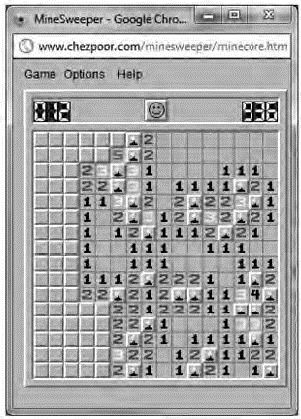
图4-5　扫雷

每个小方块埋着一个数字或者地雷，数字代表临近的方块（包括水平、垂直和对角线相邻）总共有几个地雷。在某个不是地雷的方块上点一下会显示出下面的数字。如果你觉得方块下面有地雷，就标一个小旗子。点中地雷你就输了。判断能否玩赢一个大规模的扫雷游戏也是NP完全问题。这是上面那张图里剩下的地雷。

图4-6　扫雷失败

图4-7　俄罗斯方块

当然还有俄罗斯方块。玩家平移和旋转各种下落的积木，填满一行的那一刻整行会消失，游戏目标是不让整个画面都被方块填满，坚持尽可能长的时间。

积木分很多种形状。

图4-8　俄罗斯方块的积木

经典俄罗斯方块游戏中你不知道下一块积木的形状。但即使你提前知道了各种形状的积木到来的次序，如何把俄罗斯方块玩到最好也是一个NP完全问题。

谁曾想把数独、扫雷和俄罗斯方块这些游戏玩好，就可以证明P=NP从而解决我们这一代面临的最大的挑战呢？

图4-9　魔方。图片作者为Tom van der Zanden

魔方又怎么样呢？即使是3×3×3的小魔方，一般人也得花不少工夫才能知道如何复原，而求解更大的魔方的难度可想而知。

其实不算太难。我们对于解决更大规模的魔方复原问题有一些很快的算法，它们都基于一个叫做群论的数学分支。这些算法不能保证找到全局最少步骤的解法，但是总能找到足够短的方法，从任何可能的打乱方式开始将魔方复原。

与玩好俄罗斯方块、扫雷和数独的困难程度相比，复原魔方的问题容易得出奇。

而双人对战游戏，如国际象棋、跳棋、黑白棋和围棋，它们的难度又如何呢？这些游戏的大规模版本，其难度和可满足性问题等NP完全问题的难度是相当的。但是这些双人游戏不属于NP类问题。比如我告诉你，这盘国际象棋肯定是白方赢，最后一步是三列卒吃王，你根本没法验证我的话。计算机科学家基本上都认为国际象棋、跳棋、黑白棋和围棋的难度均大于任何NP问题。