3. 线性规划

敌友国有一个熟食店叫Frenemy Fancy Franks，里面出售四种口味的香肠：法兰克福香肠、意大利香肠、德国香肠和西班牙香肠。不同种类的香肠制作时间不同，售价也有差别。Frenemy Fancy Franks应该如何安排每种香肠制作的数量，以获取最大的利润呢？

找到最优的方案就是在满足各种限制条件的前提下使收入最大化。假设制作一根法兰克福香肠的成本是1美元，意大利香肠的成本是2美元，德国香肠是3美元，西班牙香肠是4美元，且每日的总预算是1万美元。那么，1乘以法兰克福香肠的数量，加上2乘以意大利香肠的数量，加上3乘以德国香肠的数量，加上4乘以西班牙香肠的数量，结果应不超过1万。

在这类条件下进行最优化选择的问题叫做线性规划。可能的解集在高维空间形成一个几何体，叫做多面体。

早在1947年，格奥尔格·丹齐克发明了单纯形法（simplex method），这种方法能很快解决线性规划问题。单纯形法遍历多面体所有的边，直到找出最佳的解集。

既然有了单纯形法，我为什么要把线性规划放在（20世纪70年代）未分类的问题里面呢？因为在某些罕见的个例中，单纯形法无法快速求解线性规划问题。

1979年，利奥尼德·卡奇安发明了椭球算法（ellipsoid algorithm），基本思路是把多面体切分成越来越小的块，不断缩小范围并最终找到最优解。卡奇安给出了椭球算法有效性的证明，从而把线性规划分到了P类问题中。然而实践中椭球算法的耗时比单纯形法要长很多。虽然缺乏实用性，但椭球算法在之后的几十年中启发了许多更复杂的算法的诞生，因而它在学术上还是很有影响力的。

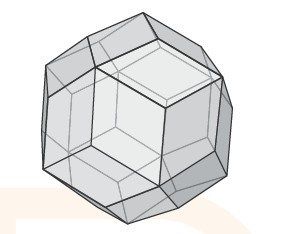
图4-12　多面体

这样一来，线性规划在理论和实践上分别都有了好的解决算法——只不过是两种非常不同的算法。

1984年，纳伦德拉·卡马卡发明了内点算法（interior point algorithm）。和单纯形法类似，卡马卡的算法遍历多面体，只不过是在内部遍历而不是表面。和椭球算法一样，内点算法也能将线性规划归属到P类，并且在经过优化后该算法的实际性能甚至高于单纯形法。

以上就是解决线性规划问题的三种非常不同的算法。第一种（单纯形）在实践上表现很好。第二种（椭球）在理论上很好。而第三种（内点）则在理论和实践上的表现都很好。能对一个在20世纪70年代末还被认为是未解决的问题给出这三份答案，是很值得人们为之自豪的进步。