6.3　搜索小规模的解

如果我们想在敌友国的2万居民中寻找数目为3的团，最原始的方法需要检查1万亿多一点种可能，这对如今的计算机不太困难。但是数目增长得太快了：4个人的团就存在6000万亿种可能；5个人的团则有26亿亿种可能；6个人的团则有880万亿亿（88后面有21个0）种可能。很快，问题的规模就超出了机器的处理能力。

对于其他NP完全问题，搜索小规模的解可能会简单一些。如果敌友国有一群人满足如下条件：即对任意一对朋友，都至少有一个人在这群人中，那么这样一群人被称为一个舒适组（very cozy group）。

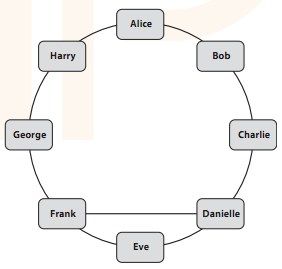
图6-8　舒适组

在这个好友关系图中，Bob、Danielle、Frank和Harry组成了一个非常舒适的组，因为每对好友关系中至少有Bob、Danielle、Frank和Harry中的一个人。

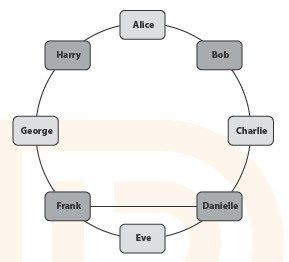
图6-9　包含4个人的舒适组

在这个好友关系图中，不存在3个人的舒适组。例如，如果我们把Alice、Charlie和Frank这3个人看做舒适组，那么就漏掉了Eve和Danielle，以及George和Harry这两对朋友。

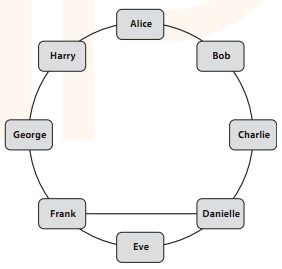
图6-10　包含3个人的舒适组

舒适组问题，即人们熟知的“顶点覆盖问题”，是卡普原来列出的NP完全问题之一。

我们来看图中的Frank。如果Frank不在舒适组中，那么George、Danielle和Eve必须在舒适组中，因为他们都和Frank是朋友关系。如果Frank有100个朋友，则要么他自己在舒适组中，要么他所有的朋友都在舒适组中。

使用这样的技巧，计算机科学家可以不用穷举就能找到小的舒适组。找到5个人的舒适组只需要检查大概100 000种可能。找10个人的组则需检查200 000种可能。30个人的组则是601 000种——所有这些用你的笔记本电脑来算基本上瞬间就能完成。搜索包含113人的舒适组需要检查1万亿种可能，其计算时间基本等于搜索3个人的团的时间。

等一下！卡普不是证明找到最小的舒适组也是NP完全问题吗？看起来寻找舒适组并不怎么困难嘛。想想敌友国有多少对好友关系。这么多的好友关系，舒适组根本不可能只用区区113人就保证每对好友中至少有一个人在其中。当舒适组的人数达到合理的规模以后，相应的必须检验的可能性的规模会变得非常大。

如果你寻找的是150人的组，有1500万亿种可能需要搜索；200个人则是10万亿亿种（10²¹）；而500人，则大概是38后面跟51个0。找到敌友国中最小的舒适组基本上是不可能完成的任务。但如果我们只是在100个人中寻找有没有舒适组，这个任务还是可以在合理的时间内完成的。