9.1　量子录像机

汤姆是波士顿人，很自然地，他也是波士顿红袜队的球迷。有一天在汤姆上班的时候，纽约洋基队客场对战波士顿，他刻意避免读到任何关于比赛的消息。下班回家后，他订了一些披萨饼，打开录像机，开始观赏几小时前就结束的这场比赛。第9局末，红袜队在二垒和三垒有人，两人出局，一人被夹杀。此时波士顿的强力击球手布莱恩·哈默走上本垒板，汤姆十分希望哈默能击中。汤姆觉得自己有点反应过度了，毕竟比赛早就结束了，哈默要么击中了，要么没击中。但是汤姆不知道是哪个结果。在汤姆看来，比赛的结果还是未被确定的，实际的结果介于输和赢之间，并且很快就会向他揭开谜底。

汤姆的真实取决于他的观测。从汤姆的观点来看，只要他没有观看到最后一刻，比赛就还没有结束，胜者还未被确定。在最后一刻之前，比赛处在一种奇怪的状态中，介于红袜队赢和输之间。

洋基队的铁杆球迷苏姗也把同一场比赛用录像机录了下来，并且和汤姆在同一时间分别观看自己的录像。苏姗和汤姆一样，不知道哈默是否能击中，如果击中那洋基队就输了。苏姗脑海中的比赛也是不确定的，是一个随机性事件，直到她看完整场比赛。

苏姗和汤姆在同一时刻、相隔200英里的两个地点观察两个随机事件。然而，他们将看到一致的结果：两个人要么都观测到哈默击打成功，要么都观测到他击打失败。不可能汤姆看到哈默击中了球而苏姗看到哈默被三振出局。两个人都不知道结果，但都确信看到的比赛结果是一样的。记录在苏姗和汤姆的录像机上的结果，以某种方式彼此纠缠在一起。

这和量子计算有什么关系？传统计算机最基本的元素是比特（bit，binary digit的简写），它只能取两个值中的一个，如赢或输、真或假。而量子计算机的基本元素叫量子比特（quantum bit）。和只能取两个值之一的比特不同，量子比特的取值能介于两个值之间。

记录在录像带上的棒球比赛并不是真的量子比特，但是它们有一些共同的属性。汤姆看球赛时，直到比赛结束，结果都是不确定的。而从他观测到比赛结束的那一刻起，结果就确定了，红袜队不是赢了就是输了，不再介于两者之间。类似地，从量子比特被观测到的那一刻起，它就变成了一个传统的比特，只能取两个值之一，而不是介于两个值之间。

量子比特可以互相纠缠，就像汤姆和苏姗的录像带那样。让两个量子比特互相纠缠，这样它们在被观测到的那一刻就总能给出相同的答案。

不过二者的相似性就到此为止了。量子比特能以复杂得多的方式互相纠缠，而这些纠缠态可被操控，从而形成计算能力。

比赛的结果是一个简单的概率，可以在一条简单的直线上取任意值。

图9-1　波士顿

五角星所处的位置代表波士顿有30%的概率会赢。汤姆看完了比赛，五角星要么左移到尽头，要么右移到尽头，至于向哪边移动则取决于比赛结果。

量子比特则可在一个圆圈上取值。

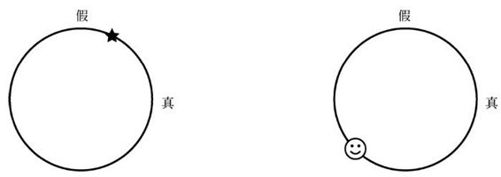
图9-2　量子比特

这张图里的五角星在二维平面中的坐标是(0.55真, 0.84假)。量子比特也可以取负值。笑脸代表的量子比特取值为(﹣0.71真, ﹣0.71假)。量子计算机能以可控的方式旋转或翻转这个圆圈。

一个量子比特可用一个二维的圆圈来表示。两个量子比特则需要用一个四维版本的圆圈来表示其状态，很难在这里画出来，甚至难以想象。30个量子比特则需要超过1万亿个维度。

这启发人们可以用量子计算机的方法解决NP问题。想想从2万敌友国居民中找出50人的团的问题。我们能用大概500个量子比特表示出所有可能的50人的集合。然后可以同时并行地处理所有的集合，并通过适当的旋转和翻转操作标记出其中能够组成团的那些集合。

我们现在有了一个“量子态”，即大概3×10¹⁵⁰（3后面跟150个0）组敌友国居民的组合状态，其中某些被标记为团。如果能用某种方式很快地把这些团从量子态中抽取出来，我们就能用量子方法快速解决团问题以及每一个其他的NP问题。当我们观测这个量子状态的时候（就好比看到录像带上比赛的结尾），我们只能看到一个结果，即敌友国中的一群人，而很有可能这群人不会组成一个团。

我们需要某种方式，让组成团的人群集合脱颖而出，从而更有可能被观测到。这可以用量子操作来实现。最笨的方法将使用和集合的个数相等次数的量子操作，即大概3×10¹⁵⁰次的量子操作，完全没有体现使用量子计算的优势。1996年，在新泽西州贝尔实验室工作的洛夫·格罗佛发明了一种更高明的量子算法，“仅仅”使用2×10⁷⁵次的量子操作。即使我们每秒做1万亿次量子操作，所需时间也大致是当前宇宙年龄的5倍。

有某些证据表明格罗佛的算法是使用量子计算机来求解NP完全问题所能达到的最好结果，所以P=NP的量子版本也不太可能成立。即使物理学家们成功造出了量子计算机，它还是无法解决我们面临的最难的问题。

这并不意味着量子计算机就没有用了。它能对纳米级别的物理系统有效地进行复杂的仿真，这将有助于揭开宇宙的一些未解之谜。量子计算机还能求解某些人们无法用传统计算机有效解决的NP问题。

1994年，贝尔实验室的另一名研究人员彼得·肖尔意识到，量子计算机能对数字进行因数分解，例如对于数字16 461 679 220 973 794 359，找到两个数5 754 853 343和2 860 486 313，并有5 754 853 343×2 860 486 313=16 461 679 220 973 794 359。他的算法工作在快速的量子计算机上，对几百位甚至几千位的大数都有效。搜索一个数的因子问题有着良好的代数结构，可被量子计算机利用。尽管我们认为因数分解对于今天的计算机是很难的问题，量子计算机则能够借此克服这些困难，分解很大的数字。而NP完全问题则缺乏这种良好的代数结构，故肖尔的算法对通用的NP问题是无效的。

当然，我们能真正使用格罗佛或肖尔的算法的前提是：有一个能工作的量子计算机。为解决今天的机器无法解决的规模可观的问题，我们至少需要上万个量子比特彼此纠缠，并在几秒的时间内是可控的。可惜的是，量子纠缠态十分脆弱。量子系统和外界环境的任何交互作用都可能引起一次“观测”，导致某些纠缠态的丧失，这对于精密的量子计算是不可挽回的灾难。

甚至对于两个量子比特，目前物理学家还不能使其达到完美或接近完美的量子纠缠态。计算机科学家采用所谓量子纠错的方法来设计算法，以处理中等规模的量子纠缠。即使如此，我们不知道如何在超过5个量子比特之间创造出显著数量的纠缠态。可能存在某些自然界的基本法则，阻止量子之间在一段足够长的时间内处于显著的纠缠态，也可能这只是一个棘手的工程问题。我们还是让物理学家来解决这个问题吧。

还有其他利用量子效应来进行计算的方法，如量子绝热系统，或量子退火，而它们也分别有自身的技术和计算局限性。一个叫D-Wave的公司宣称建造了基于这些技术的机器，但这些机器的计算能力能否超过人们的桌面电脑，还有待评估。

即使我们发现了建造真正的量子计算机的方法，这些机器仍然是为特殊用途而建造的，如因数分解或者量子系统的仿真。它们也许有助于破解密码，以及加深人们对宇宙的本质的了解，但不太可能用它们来求解NP完全问题，或加快电子表格的运行速度。