1. 图的同构问题

在敌友国流行着一个叫“刀剑征程”（Blade Quest）的MMORPG（大型多人在线角色扮演游戏）。游戏中每个玩家都会起一个新名字，操纵一个虚拟角色（avatar）去和其他玩家的虚拟角色进行互动。敌友国的敌友关系也被引入了刀剑征程的世界。在现实中互为朋友的居民，他们在游戏中的虚拟角色也是朋友关系；相反，现实中的敌人在游戏里也是敌人。

Isabel、John、Kevin、Laura、Molly和Nancy是几个喜欢玩刀剑征程的敌友国居民。

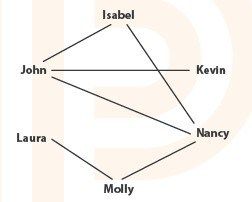
图4-10　玩刀剑征程的居民

这6个人在游戏中的虚拟角色的名字是Achris、Bolem、Chyrard、Degarald、Enthrr和Fev，但是哪个虚拟角色对应哪个真人是保密的。在刀剑征程中，这几个虚拟角色也有一个好友关系图。

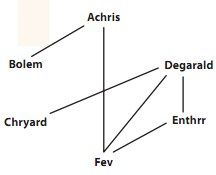
图4-11　刀剑征程中的虚拟角色

Laura看了这两张图，就在游戏里给别的玩家发了一个消息：“我知道你在现实中是谁。”你能猜出来吗？

这两张图存在唯一的对应方式，即Isabelle在游戏中对应的虚拟角色是Enthrr，John是Degarald，Kevin是Chryard，Laura是Bolem，Molly是Achris，还有Nancy是Fev。我们可以验证一下，如Molly在敌友国的朋友是Laura和Nancy，与之对应，在刀剑征程中Achris的朋友是Bolem和Fev。

好友关系图之间的映射被称为图的同构问题。有可能存在多种映射，也可能不存在，这取决于给定的图集。图的同构性属于NP类问题：如果知道了谁对应谁，你可以通过逐对查看好友关系在两张图中是否一致来验证这个解的有效性。

但是图同构是否属于P，即我们是否能找到图之间的映射（假设存在）的有效算法，还是未知的。我们也不确定图同构是NP完全的，而出于多种技术原因，计算机科学家也不认为它是NP完全的。图同构属于另一小撮问题，其难度比P问题大，但比不上哈密顿回路、最大割等NP完全问题。