6.4　近似计算方法

也许我们没有问题的最佳答案，但通常一个不坏的答案就足够好了。

比如NP完全的旅行推销员问题，即找到访问多个城市的最短路线。

如果我想到50个城市旅行，最短的路线是180万英里，而我已经找到了一个需要181万英里的路线，通常大可不必为多走的1万英里劳心费神。

换一个角度讲，如果走1英里要花费1美元，而我旅行的收入是180.5万美元，那么180万英里和181万英里的差别，可能就是挣5000美元和赔5000美元的差别。如果我对旅行计划作出一点点的改进，比如180.3万英里，那我就可以扭亏为盈了。

虽然地图上的旅行推销员问题是一个被认为难以有效解决的NP完全问题，但是我们可以找到非常接近最优解的旅行路线。桑吉弗·阿罗拉和乔·米切尔给出了一个算法，原理是先将地图切分为许多小块，然后在所有小块中找到小段的最佳路线，最后通过一种高明的方式将这些小段的路线连接起来。

如下图中的71 009个中国城市。

图6-11　中国城市

我们把一个细密的网格套在地图上，然后在每个小格中求解旅行推销员问题。如果某个小区域的城市太多，那就进一步把该区域细分成更小的网格。

用这种技术，我们可以在合理的时间内，找到与最优方案只差百分之几的方案。

图6-12　中国城市的网格

如果所有NP问题都有这么好的近似计算方法，那么P/NP问题几乎就不重要了。然而生活没有那么轻松。比如团问题，即找到一大群互为朋友的人。目前还不存在任何通用的方法可以估算最大团的问题。敌友国可能存在2000人的团，但在合理的时间内，我们连15人的团都找不到。

如果P=NP，我们就能有效地找到全局最大团。这被证明是能稳定地找到团的唯一方式，哪怕是寻找人数是最大团的0.1%的团，也只能采取这种方式。发现任何能比这更好地通过估算来解决团问题的算法，都将令P=NP，即有效地解决团问题本身。

许多NP问题既不像团问题这样难以估算，又不像地图上的旅行推销员问题那样容易估算。让我们回过头再来看看舒适组问题。

像这样一个小规模的例子，我们通过穷举就能得出最小的舒适组有4个人，例如Frank、Danielle、Harry和Bob。假设我们不知道这一点，让我来描述一个估算最小舒适组的简单的算法。

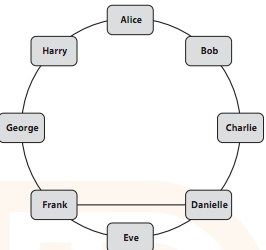
图6-13　舒适组II

首先任选一对朋友，比如Alice和Harry，并标记他们。

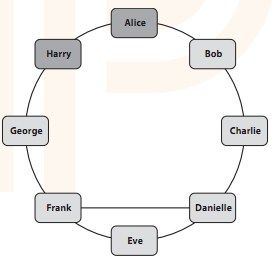
图6-14　舒适组II，2人被标记

找到另一对没被标记的朋友，然后也标记他们。

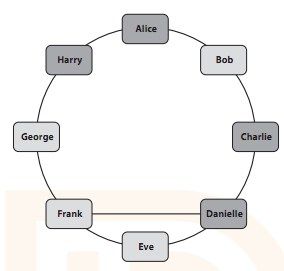
图6-15　舒适组II，4人被标记

重复上一过程直到找不到未被标记的朋友。

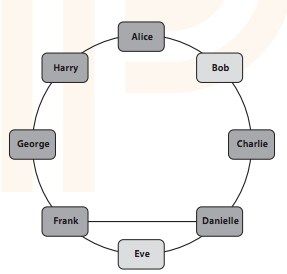
图6-16　舒适组II，6人被标记

最后，所有被标记的人组成的将是一个舒适组。

在这个示例中，我们得到了一个6人的舒适组。每个舒适组都要从被标记的3组好友中每组至少选一个人，所以人数不能少于3人。那么最好的舒适组的人数应该在3到6之间。

这个算法适用于所有的好友关系图。如果我们的算法找到了人数为100的舒适组（即总共添加了50对好友），那么我们知道最好的舒适组应该在50到100人之间。

我们总能找到一个舒适组，它的人数是最小舒适组人数的2倍。我们能得到比这好很多的结果吗？也许不能。

如果P=NP，我们就能轻松找出最小的舒适组。但如果P≠NP呢？一般地讲，不可能找到比最小人数多36%或更小的舒适组。任何能找到比最小人数多36%的舒适组的算法，都能被转化为一个可解决所有NP问题的算法。这个转化的过程与一系列在1990年到2005年之间证明的艰深结论有关。

上面介绍的简单算法通过逐个添加一对好友，能找到最多两倍于最小人数（也就是比最小人数多100%）的舒适组。如果P≠NP，那么我们能希望的最好结果就是找到比最小人数多36%的舒适组。我们有可能找到比最小人数多50%的舒适组吗？

为解答上述问题和其他相关问题，计算机科学家萨布哈什·霍特引入了一种他称为独特游戏（unique games）的问题，该问题是地图填色问题的一个变种，增加了一些约束相邻地区填色方式的规则。独特游戏猜想是说独特游戏是NP完全的，人们至今无法判断该猜想是否为真¹。

_{1 关于独特游戏和独特游戏猜想，参见维基百科页面 http://en.wikipedia.org/wiki/Unique_games_conjecture。——译者注}

如果独特游戏猜想是真的，我们甚至可以进一步约束近似计算的能力。霍特证明，如果该猜想为真，那么不能找到比最小人数的2倍只少一点的舒适组。如果该猜想为真，我们不能得到比上述简单算法好很多的结果。