6.2　启发式方法

17世纪的伐木工在测量中经常用他们拇指的长度来大致度量1“英寸”的距离。“拇指规则”这一俗语可能就源自于此，意思是在决定某些问题答案的过程中使用一种不太准确但大致可用的简化方法。谚语“朝霞不出门，晚霞行千里”给出了一种粗略但通常相当可靠的预测天气的方式。摩尔定律本身也提供了一种粗略地预测未来计算机的计算能力的方法。

计算机算法同样也是一种过程。启发式方法是一种原理类似“拇指规则”的算法，虽然不能保证给出正确的答案，但可以对大多数你想解决的问题给出答案。人们在认识到某些问题是NP完全问题之前，就给出了它们的启发式解法。几十年来，我们为解决各种困难的问题发明了很多复杂的启发式方法。虽然这些方法不适用于任意一个NP完全问题的所有情况，但有助于根据特定的情况解决人们所面临的部分问题。

让我们来详细分析一个地图填色问题的简单而强大的启发式方法。在第3章我们证明了为美国地图填色至少需要4种颜色，才能保证所有接壤的州具有不同的颜色。

加利福尼亚、俄勒冈、爱达荷、犹他、亚利桑那这几个州围绕着内华达州成为一圈。至少需要三种颜色为加利福尼亚、俄勒冈、爱达荷、犹他、亚利桑那这几个州填色。而内华达州并非个例。肯塔基州周围围绕着田纳西、弗吉尼亚、西弗吉尼亚、俄亥俄、印第安纳、伊利诺伊和密苏里这几个州。同样，你需要至少3种颜色填充这几个围成一圈的州，再用第4种颜色填充肯塔基州。

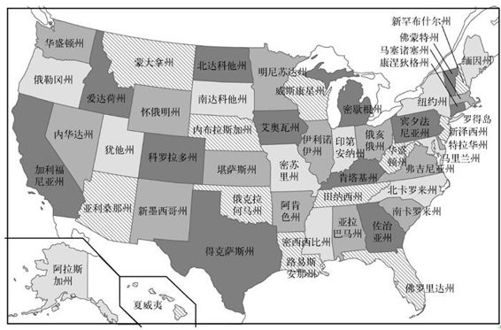
图6-2　美国地图

一张地图只要上面的某个地区被奇数个相邻的地区所环绕，那么它最少需要4种颜色。

这里有一张亚美尼亚各州的地图。

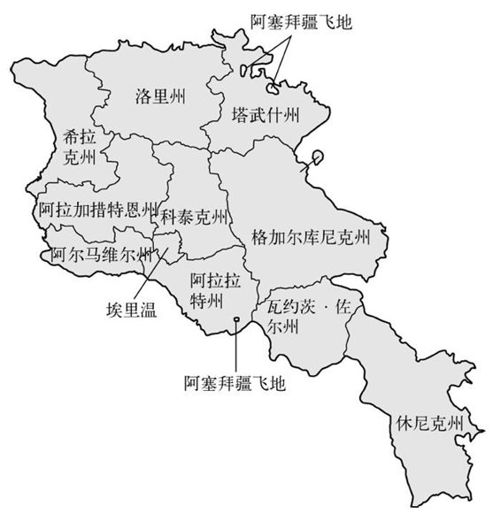
图6-3　亚美尼亚

只有两个州完全在亚美尼亚内部，不与其他国家接壤。科泰克州（Kotayk'）有6个邻州，而首都埃里温（Yerevan）有4个邻州。每个不靠海的省都有奇数个邻州。所以启发式方法告诉我们，也许能用3种方法为这张地图填色。事实上真的可以。

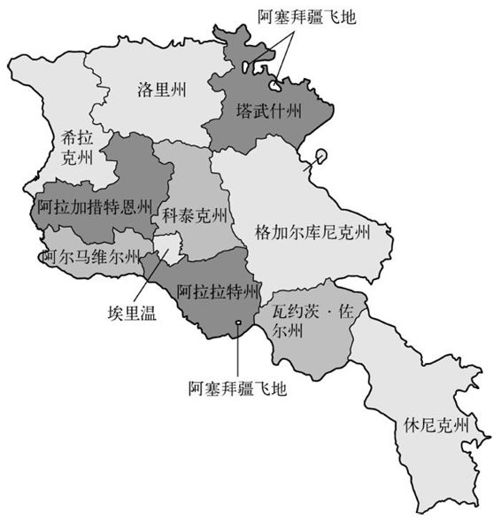
图6-4　填色后的亚美尼亚地图

瑞士有5个邻国：法国、意大利、奥地利、列支敦士登和德国。虽然邻国数为5，我们还是可以用3种颜色填充这张地图。

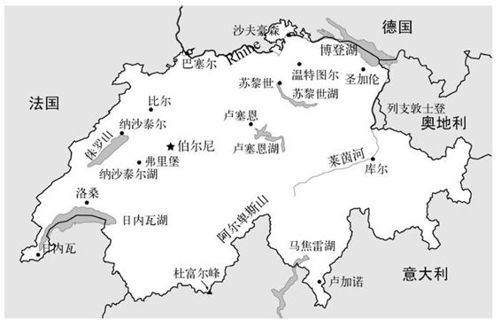
图6-5　瑞士

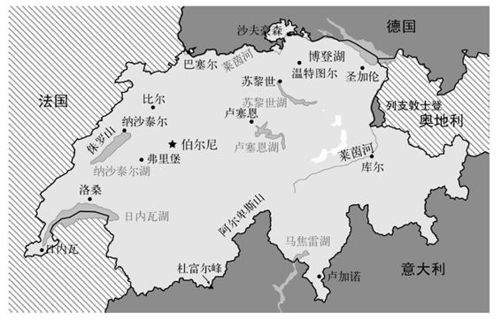
图6-6　填色后的瑞士地图

列支敦士登将瑞士和奥地利的国境线分割为两段，所以对于地图填色这个问题，我们需要把奥地利算两次。重要的不是邻国的数量，而是国境线的数量。瑞士有6段国境线，6是偶数。而且只有外围的国境线才算数，对于那些完全位于其他国家领土内部的国家（如意大利内部的梵蒂冈），我们不把它们的国境线计算在内。

如果这个启发式方法总能给出正确的答案，那么它将是一个解决NP完全的三色填充地图问题的有效算法，进而我们就有了解决所有NP问题的有效算法，即P=NP。读到这里你可能猜到了，这个启发式方法不总是有效。

令这个启发式方法失效的反例有两个。

• 地图上有一个湖将两个地区分隔开来，如密歇根湖将伊利诺伊州和密歇根州分隔开来。

• 地图上有4个以上的地区汇聚于同一点，如亚利桑那、新墨西哥、科罗拉多和犹他这四个州。

在填充美国地图时这些反例不重要，因为我们已经知道填充美国地图至少要4种颜色，这甚至没有把填充湖面的蓝色计算在内。

然而这个启发式方法在现实世界中很少失效。为说明问题，让我们来看看虚构的敌友国地图。虽然每个省都有偶数个邻省，但还是不能只用3种颜色为敌友国地图填色（不包括湖面的蓝色），以确保两个接壤的省的颜色不同。

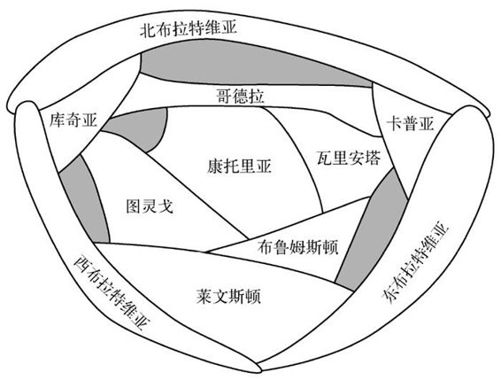
图6-7　敌友国地图

每个省都和4个其他的省接壤。没有一个省被邻省围绕成环，因为有湖水从中阻隔。启发式方法告诉我们可以只用3种颜色填充这11个省，但实际上这不可能，只用三色必然导致邻省同色的情况。启发式方法在敌友国能否用三色填充地图的问题中给出了错误的答案。

可满足性理论及其应用国际学术年会（The International Conference on Theory and Applications of Satisfiability Testing）是可满足性问题相关领域研究人士的一个交流和展示的平台，尤其重视优秀的启发式方法。会议组织了SAT¹竞赛，比拼各种计算机算法求解可满足性问题的能力。竞赛用的可满足性问题有的是随机生成的，有的是特意构造出来以提高难度的，还有的则是实际应用中产生的。这些算法中有许多都能解决某些达到一百万个变量规模的可满足性问题。

^{1 SAT为可满足性问题（satisfiability）的前三个字母。 ——译者注}

启发式方法并不总能奏效。没人能在SAT竞赛中取得完美的成绩。但通常来讲，对各种计算技巧的巧妙使用，再加上当今最快的机器的强劲火力支援，有些算法甚至能求解规模很大的最优化问题。