3.3　牵线搭桥

在敌友国，一段美满的姻缘几乎完全取决于双方是否是很好的朋友。然而敌友关系的分布完全没有规律，有些幸运儿可能碰巧找到了合适的人选，剩下的人则很难找到一个好伴侣。

敌友国的研究者意识到可以用他们的数据来为社会服务，让成功婚姻的数量最大化。于是他们在网站上招募了200个志愿者，其中一半是男性，一半是女性，所有人都是异性恋。他们想尽可能多地为合适的男女牵线搭桥。

一共需要搜索多少种可能性呢？和第一个男性配对的女性人选有100个可能。做出选择后剩下的99个女性可能和第二个男性配对，然后是98个女性和第三个男性配对，如此等等。这样所有的可能数是100乘以99乘以98乘以……乘以2乘以1，这个值被称为“100的阶乘”，写作100!，这个数有158位，比googol还大。googol这个名字是数学家爱德华·卡斯纳九岁的侄子起的，当时卡斯纳想给1后边跟100个0的数起名。

互联网公司Google得名于对googol的错误拼写，它是对该公司搜索引擎所处理的海量数据的一个形象但非常不准确的表示。互联网这种庞然大物（实际上无法测量它有多大）所包含的信息量无论分得多细，都还远远达不到googol这个数量级。所以，即使动用全部的计算机算到地老天荒，也不可能搜索googol数量级的信息，更别提100!了。

然而敌友国研究者还是能找到成功配对数的最大可能值，只需换一个高明的算法即可。下边这张图显示了哪些男女志愿者是朋友关系。

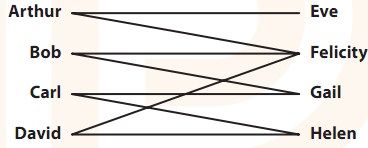
图3-2　敌友国的男女们

让我们看看谁跟谁可能是天作之合。首先我们把Arthur和Eve凑成一对。Bob和Felicity这对朋友还没有在一起，让我们促成他俩，同样祝福Carl和Gail。现在我们有了一张新图，虚线表示我们做出的配对选择。

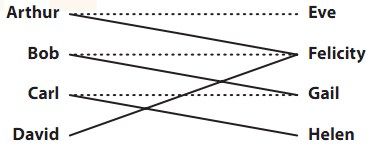
图3-3　部分配对的男女们

这下不存在能够配对的朋友了，这是可能的配对结果中最好的吗？不一定。

David没有伴侣，但他和Felicity是朋友，而Felicity和Bob在一起。Bob和Gail是朋友（但我们没有撮合他俩）。Gail和Carl是一对。Carl和没有伴儿的Helen是朋友。如果我们拆散Bob和Feliciy，再坏了Carl和Gail的好事，然后重新配对，那么这下所有人都成功配对了。

图3-4　全部配对的男女们

第二张图中连接两个人的实线和虚线的序列，叫做增广路径（augmenting path），它可以用来增大配对的数量。1957年，克劳德·伯杰证明任何未达到最大可能配对数的匹配方式都对应一个增广路径。敌友国理工学院的计算机科学家写了一个简单的算法来找到这些增广路径，结果让参加实验的98%的人都成功配对。

不久以后，敌友国最高法院裁定，允许同性结婚。于是学院在网站上张贴启事，招募所有性别取向的志愿者。这下关系图更复杂了，出现了许多彼此交叠的三角恋爱关系，如下所示。

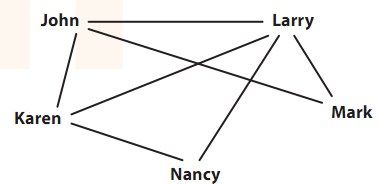
图3-5　打破传统的男男女女

这导致寻找增广路径的简单算法不好用了。研究者转而求助于杰克·埃德蒙兹的工作。在1965年，埃德蒙兹写了一篇标题很文艺的论文“路径、树木与花朵”（Path, Trees and Flowers），里面介绍了一种稍为复杂的方法，能够在广义好友关系图中找出增广路径。敌友国理工学院采用埃德蒙兹的思路，从而能够让97%的参与第二个实验的人找到合适的伴侣。

“路径、树木与花朵”中的思想，除了能为解决广义好友关系图中的配对问题提供一种有效的方法，还有更大的影响。埃德蒙兹的算法为100个人找到最佳匹配需要大概100⁴个计算步骤。对于今天的计算机，计算100⁴（即1亿）次一点也不费劲，而更原始的穷举方法大概需要的计算步骤数是2后边跟78个0。埃德蒙兹在论文里还写了很多题外话，探讨高效算法的本质。他意识到不存在能够完全抓住“效率”直观概念的严格定义，于是他试着提出自己对高效的见解，即存在一个计算方法，它解决这种规模的问题所花费的时间是“算术级别的”，比如100⁴、100²或100¹²。后来这一类型的问题有了另一个人们更为熟知的名字——P（代表polynomial，多项式级别的，它代替了埃德蒙兹的“算数级别的”），人们用它来指代那些可以高效解决的问题。这就是P/NP问题中P的一面。