7.2　电路

现代计算设备的核心都有一块集成电路板。

集成电路由上百万或上百亿个微小的晶体管组成。晶体管是一种能放大并控制电子脉冲的元件，它们实现了逻辑门（gate），即一些构建在带有电荷的导线上的简单逻辑操作。

图7-5　电路，图片由宾夕法尼亚大学电子和系统工程系提供

我们首先来看简单的导线。每根线要么带有高电压，要么带低电压，只能取两个值中的一个，这经常被表示为开和关、1和0，或是真和假。我们将这些二元系统称之为比特（bit），即“二元数字”（binary digit）的简称。

一根导线做不了什么，几根在一起也能力有限。为了构成计算能力，我们要对导线上的信息进行一些逻辑操作。其中最简单的就是翻转导线的值，这叫做非门（NOT gate）。

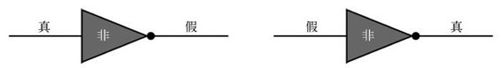
图7-6　非门

如果非门的左边有电压，那么右边就没有，反之亦然。

计算的真正力量并不是对单个导线的操作，而来自于将多条导线的值以某种机制合并。与门（AND gate）将2条或更多条导线的值合并为一个值，该值仅在所有导线的值都为真时为真。或门（OR gate）将2条或更多条导线的值合并为一个值，该值在至少有一条导线的值为真时为真。

图7-7　与门和或门

我们能用这些简单模块构建更复杂的逻辑操作。比如，两条导线做异或操作（Exclusive-OR）的值只在仅有一条导线的值为真时为真。

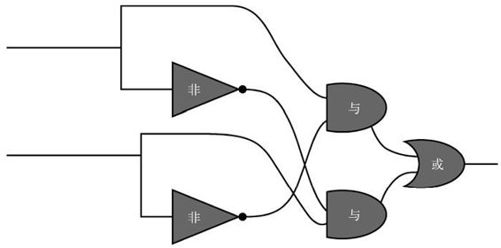
图7-8　异或门

每一个函数，无论它多复杂，都能用与、或、非三种门组成的电路来计算。让我们回顾一下敌友国的团问题，即我们想找到一群彼此互为好友的人。我们可以用一个与门来表示Alice、Bob和Carol是否互为朋友。

图7-9　与门

假设我们想知道在Alice、Bob、Carol、David和Eli中是否存在3个人的团。我们用图7-10中的电路来计算这个问题。

这个电路有10个与门，表示的是从5人里面找出可能成团的3个人，共有10种可能。假设我们现在要从敌友国的2万人中找出50人的团。直接转换的电路将有

3 481 788 616 673 927 174 126 704 329 430 033 822 428 741 136 969 800 292 509 234 146 086 195 855 824 730 457 281 170 250 134 309 383 506 694 008 809 661 825 431 661 561 845 957 650 386 210 936 569 600

个与门，规模大到无法实现。

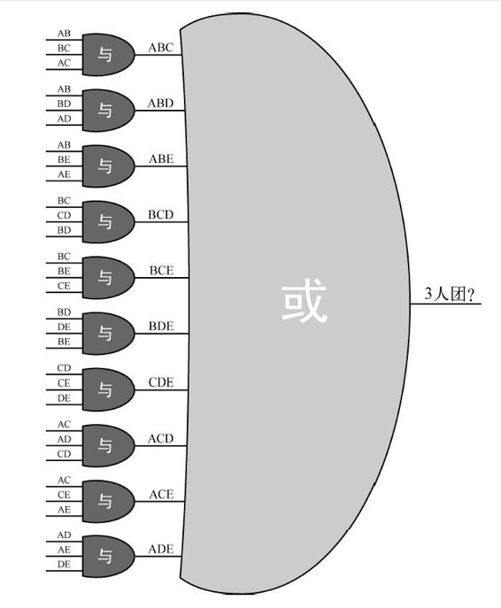
图7-10　团问题的电路

这和P/NP问题有什么关系呢？每一个P中的问题（即每一个能被高效地求解的问题），都对应一个规模相对较小的由与、或、非门构成的电路，并且该电路能够求解该问题。如果我们能证明某些NP中的问题（例如团问题），不能对应一个小规模的电路，那么就证明了NP≠P。

那是否能证明团问题不能对应小规模的电路？这个问题和P/NP问题密切相关，同样也是未知的，尽管大部分计算机科学家都相信团问题不对应小规模的电路，正如他们相信P≠NP一样。

看看我们上面为团问题构造的电路。注意其中没有非门。不是所有的问题都能对应不含非门的电路，比如简单的异或操作的电路就必须包含非门。然而，团问题就可以用只有与门和或门的电路来计算，尽管这些电路的规模极为庞大。

1985年，莫斯科斯捷克洛夫数学研究所的一名学生亚历山大·拉兹波洛夫证明，如果电路只包含与门和或门（没有非门），那么任何能求解团问题的电路必须使用数量极多的逻辑门。这并没有解决P/NP问题。因为虽然可以在求解团问题的电路中不使用非门，但说不定使用非门将显著降低电路所需的逻辑门的数量。

尽管如此，拉兹波洛夫的工作曾被看成是有望解决P/NP问题的突破性进展。我的博士生导师迈克尔·塞普斯当年认为P/NP问题的解决指日可待。需要做的只是对拉兹波洛夫的方法稍加改进，让它也适用于非门。如果成功，那么作为NP问题之一的团问题，其求解电路必须要使用数量极大的与、或、非三种逻辑门。所以团问题没有高效能的算法，因为所有高效能的算法都可转化为小规模的电路。这样一来，团问题属于NP但不属于P，从而证明P≠NP。不幸的是，生活并没那么简单。

拉兹波洛夫发表的那些论文是用俄文写的。在论文到达美国后，塞普斯召集了几个苏联学生，大家仔细地进行翻译，并且盼望着拉兹波洛夫的下一篇论文能给P/NP问题画上一个圆满的句号。拉兹波洛夫后来发表了更多优秀的论文，但其中没有一篇是给出P≠NP的证明的。

在第3章我们介绍过敌友国的配对问题，即按好友关系为敌友国的一些居民牵线搭桥。配对问题和团问题一样，也对应只使用与门和或门的电路。证明团问题对应需要大量与门和或门的电路所用的方法，同样也适用于配对问题。任何只用与门和或门解决配对问题的电路，都需要极大数量的逻辑门。

和团问题不同，我们有解决配对问题的高效算法。所以，配对问题存在使用与、或、非三种逻辑门的小规模电路。非门对于求解配对问题不是必要的，但是使用非门会显著降低电路所使用的逻辑门的数量。看上去十分低级和简单的非门，竟然蕴含着巨大的力量。

这个事实让那些企图利用拉兹波洛夫求解团问题的方法来解决P/NP问题的尝试遭受了极大的挫折。即使证明了某个问题在只使用与门和或门时电路规模很大，也并不能保证在引入非门后电路的规模仍然会很大。后来拉兹波洛夫的工作澄清了这方面的问题。他明确地指出了他的证明在考虑到非门时变得分崩离析，并且无法修补。

后来，拉兹波洛夫和卡内基梅隆大学的史蒂文·鲁迪赫引入了“自然证明”（natural proof）的概念。自然证明涵盖了电路的各种证明方法中的很大一部分，并给出了很强的证据表明不可能用这些方法解决P/NP问题。

同时，使用非“自然”的、基于本章前面提到的悖论思想的方法来构造电路的尝试，也取得了一些小小的进展。然而试图通过“证明某个NP问题需要大规模的求解电路”的方法来找到P/NP问题的答案，可能性已经变得微乎其微。