6.1　蛮力

计算机很快，甚至是你桌上或口袋里的那些计算机，也快到不可思议，以至于它们可以通过使用“蛮力”搜索所有可能的方案，来解决一个中等规模的问题。

以前可不是这样的。在斯蒂芬·库克将P/NP问题呈献给世人的1971年，英特尔公司发布了它的第一个微处理器芯片——Intel 4004。Intel 4004是第一个包含整个CPU的芯片，也是第一个商业化的微处理器。Intel 4004当时的运行速度是每秒执行92 000条指令。

以库克的可满足性问题为例，设共有20个变量，考虑一个简单的算法，它会遍历并尝试所有让每个变量分别为TRUE或FALSE的解集。如果验证每个解需要100步，那么我们可以在19分钟内判断某个表达式是否能被满足。这个时间不是特别长，毕竟用20个变量表示不了多少内容。

解决一个25个变量的问题需花费10小时，而求解30个变量的问题将超过13天。一个40个变量的问题，如果按1971年的计算能力，将算到2009年。

这段时间里，英特尔每年都会发布很多型号的处理器。让我们从2009年选一个型号，Intel i7-870，它每秒执行的指令数是29.3亿条（是Intel 4004的3万多倍）。用这个速度，求解40个变量的问题将花费大概10个小时。也就是说，如果你在1971年想求解一个40个变量的问题，你可以选择花38年玩自己的手指，然后用2009年的科技解决这个问题，这比从1971年就开始用当时的科技来计算还要快。

针对某些其他的NP问题，算例的规模可以更大。NP完全的旅行推销员问题是指找到访问许多个城市的最短路线。用所谓的分割面法，我们可以用很短时间解决1万个城市规模的旅行推销员问题。美国人口超过500的城市共有13 509个，图6-1是穿过这些城市的最短路径。

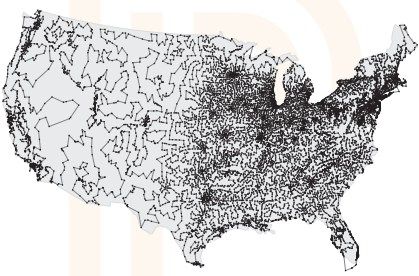
图6-1　500人以上城市的旅行推销员问题

对于其他的NP问题，可能性的数目大到连解决中等规模的问题都不太可能。

虽然我们即将逼近计算机速度的物理极限，但随着摩尔定律反映出的芯片上核心处理器个数的快速增长，人们仍然期望计算机的运算能力持续出现戏剧性的增长。这将有助于未来更大规模的NP完全问题得到解决。然而问题的复杂度也会随着规模的扩大迅速增长。所以别指望能在近期解决150个变量的可满足性问题，或是找到2万个城市之间的最佳旅行方案。