4.1　第一个NP完全问题

汤姆·赫尔在1970年担任多伦多大学计算机科学系的主任，他想聘用斯蒂芬·库克，当时加州大学伯克利分校刚刚拒绝了库克的终身教授职位申请。库克喜欢帆板运动，于是赫尔带他到安大略湖玩，给他展示在多伦多附近也能进行帆板运动，和旧金山湾是一样的。这个小伎俩奏效了，斯蒂芬·库克于1970年秋天加入了多伦多大学的教席。当年的赫尔真可谓慧眼识珠，因为在那之后不久，库克就成为加拿大最著名的计算机科学家。

库克研究逻辑学和计算机科学的联系。那年秋天，他向即将在来年五月召开的第三届ACM计算理论年会（ACM Symposium on the Theory of Computing，STOC）提交了一篇论文。这篇论文最初的结论已经被遗忘了，不过它在当时引起了足够大的兴趣，被安排在会上宣读。在准备会议期间，库克重写了论文以加入最新的工作成果，而这篇名为“理论证明过程的复杂度”（The Complexitiy of Theorem-Proving Procedures）的论文，将首次把P/NP问题呈现在世人面前，进而改变历史。

为更好理解库克的论文，让我们回头看看上一章的团问题。团是一群互为朋友的敌友国居民。在下面这张好友关系图中，Alex、Cathy和Eric是一个团，而Alex、David和Eric则不是，因为Alex和David是敌人而非朋友。

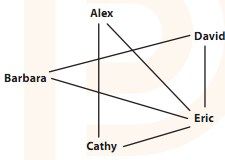
图4-1　团

你可能记得，在敌友国有一个半地下社会组织叫阿尔法会，据说里面的成员都互为朋友，也就是说他们构成一个很大的团。假设阿尔法会真的是一个团，我们能否从上面的好友关系图看出一些端倪？首先不能排除任何一个人是阿尔法会成员的可能。Alex可能在阿尔法会，David也有可能。但是Alex和David不可能同时在阿尔法会，因为他们是敌人。所以要么Alex不在阿尔法会，要么David不在。让我们把这个逻辑表达式写下来。

Alex not in Alpha Society OR David not in Alpha Society

这里的OR不具有排斥性，即有可能Alex和David都不在阿尔法会。由于Alex和Barbara是敌人，所以我们也知道这两个人不可能同时在会里：

Alex not in Alpha Society OR Barbara not in Alpha Society

这两个逻辑表达式必须同时为真，所以我们有：

(Alex not in Alpha Society OR David not in Alpha Society) AND
(Alex not in Alpha Society OR Barbara not in Alpha Society)

既然Barbara和David是朋友，他们可能都在阿尔法会，然而这个逻辑与上述表达式并不冲突。把完整的关系图用逻辑表示出来，我们得到：

(Alex not in Alpha Society OR David not in Alpha Society) AND
(Alex not in Alpha Society OR Barbara not in Alpha Society) AND
(David not in Alpha Society OR Cathy not in Alpha Society) AND
(Cathy not in Alpha Society OR Barbara not in Alpha Society)

如果Alex、Cathy和Eric在阿尔法会，而Barbara和David不在，表达式为真，因为每个OR项中都因存在不是会员的人而得到满足。然而，如果Alex、David和Eric在会中，则表达式为假：(Alex not in Alpha Society OR David not in Alpha Society)这部分不满足，因为Alex和David都在会中。

表达式很好地表达了团问题。当且仅当阿尔法会的成员们组成一个团时，表达式为真。

我们可以为敌友国的2万居民生成一个类似的逻辑表达式，将它简写为Φ。Φ可能很长，有几百万个字符，但是计算机能很容易地存下它。如果阿尔法会真是一个团，则表达式为真。

我们有另一个表达式Ψ50，它在阿尔法会有至少50个成员时为真。我不想具体讲如何写出Ψ50，它的构造方法和最早的电子计算机做加法的方式是一样的。

如果把两个表达式结合起来，我们就得到(Ψ50 AND Φ)，它在“阿尔法会是一个团，且至少有50个成员”时为真。反过来说，如果阿尔法会令(Ψ50 AND Φ)为真，那么它是一个至少有50个元素的团。

假设我们有一个快速算法，它能告诉我们给定的逻辑表达式是否能被满足。如果我们给它(Ψ50 AND Φ)，然后它回答：“是的，(Ψ50 AND Φ)可以被满足。”则敌友国存在一个50人的团。如果(Ψ50 AND Φ)不可以被满足，则那里不存在这样的团。解决了这个可满足性问题，你就能解决团问题。

我们刚刚描述了一个计算机科学中最关键的概念：归约。我们把寻找团的问题归约到检查逻辑表达式的可满足性的问题。现在只要我们有解决可满足性问题的算法，就可以通过很容易的变换，得到团问题的求解算法。团问题的求解至少和可满足性的求解一样容易。如果可满足性是容易求解的，那么团问题也是。如果团问题没有有效解法，那么可满足性问题也没有。

能归约到可满足性问题的不仅是团问题，而且还包括我们前面讨论过的其他NP问题，包括旅行推销员问题、哈密顿回路、最大割和地图填色问题。事实上，斯蒂芬·库克证明了NP中的每一个问题都能通过某种方式归约到可满足性问题。解决了可满足性问题，你就能解决所有的NP问题。如果你有解决可满足性的有效算法，我们就能快速解决所有容易检查特定解有效性的问题，也就是说证明了P=NP。只要你有一个解决可满足性的有效算法，那么克雷研究所提供的几百万美元奖金就是你的了。

1971年5月4日，在当时的俄亥俄州榭柯高地斯托弗的萨默塞特酒店召开的STOC上，斯蒂芬·库克宣读了自己的论文。

结果表明，可满足性问题可以作为一个相对有用但尚未存在有效计算方法的待选课题来研究，并且我认为值得投入更多精力来证明这个猜想。找到它的证明将可能带来重大的突破。

P/NP问题从此诞生了。