3.7 分组

敌友国小学的老师想把500个学生分成两组。每个人都想和朋友在一起，所以老师想尽可能避免把一对好友分到两个组去。让我们用“递棍儿”游戏中的那张好友关系图来看看。

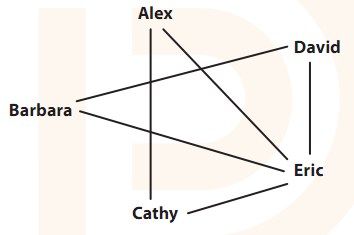
图3-15 　小学

最好的分组方法是把Alex和Cathy放在一组，Barbara、David和Eric在另一组，这样只拆散了两对好友，Alex—Eric以及Cathy—Eric。不存在只拆散一对好友的方案。

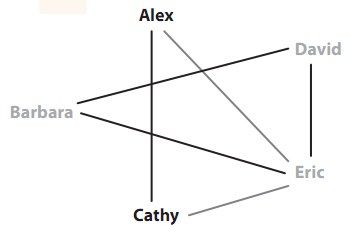
图3-16　小学的分组

敌友国小学的校长向学院求助。有很多有效的方法可以解决这个问题，它被称为最小割问题，因为老师想把被分割的好友数减到最小。研究者针对这500个学生给出了一个很好的分组方案，只拆散了17对好友。

从此以后所有人都过上了快乐的生活。说“从此以后”不太准确，事实上只过了一天，老师就发现，把很多互为仇敌的小孩分到一组太糟糕了，比拆散好友更不可取。于是校长回到学院，请研究者找到一种把尽可能多的互为敌人的学生分到不同组里的方案。校长觉得第一次的分组问题解决得那么轻松，这次应该也不会太难。校长想错了。

在这个新问题里，研究者需要尽可能多地把敌人分割开，这叫做最大割问题。但是不像最小割问题，计算机科学家不知道哪种算法能最大化被分割到两个组的仇敌数目。

也不是完全无计可施。学院利用1995年由米歇尔·戈麦斯和大卫·威廉森写的算法，找到了一个将1321对敌人分割到两个组的方案。尽管没能找出最好的方案，但他们知道不存在把1505对及以上的敌人分割到两组的方案。校长有点失望，他以为学院能找到最好的方案，但现有方案也还算合理。从此以后所有人都过上了更加快乐或更加郁闷的生活。