3.5　“递棍儿”

让我们看看一个求解简单的问题，怎样经过一点小小的改动，就变成一个非常难求解的问题。

敌友国的小孩子们玩一种叫“递棍儿”的游戏。他们把一个小棍子传来传去。“递”的意思是在把棍子从一个孩子传到另一个时，两个人一起把它握住。

规则有两条：

• 只能给你的朋友递棍儿；
• 每对朋友之间必须递一次棍子，且只能递一次。

假设5个小孩在玩这个游戏。

从Barbara开始，她把棍子递给Eric，Eric递给Alex，然后棍子依次经过Cathy、Eric，最终被递给David，游戏成功结束。

图3-6　孩子们

玩了几次孩子们很快发现游戏能成功结束的前提是，拥有朋友个数为奇数的人不能超过两个：如David和Barbara分别有1个朋友，是奇数，而Cathy和Alex分别有2个和4个朋友，是偶数。为什么呢？因为除了第一个和最后一个人，其他人接棍子的次数和把棍子递给朋友的次数必须相等，所以这些人中间的每个人经手棍子的次数应该是偶数。

如果每个孩子都有偶数个朋友，那么游戏也能玩成，只要保证开始和结束时是同一个人就可以了。

比如孩子们可以这样传棍子：从Alex开始，棍子依次经过Eric、David、Barbara、Eric、Cathy，最终回到Alex手上。

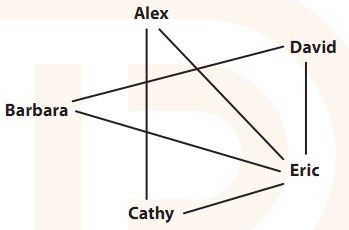
图3-7　每个孩子都有偶数个朋友

“递棍儿”的灵感来自19世纪的一个著名难题。在普鲁士的哥尼斯堡（今俄罗斯加里宁格勒）有七座桥横跨于普雷格尔河上，请看这张老地图。

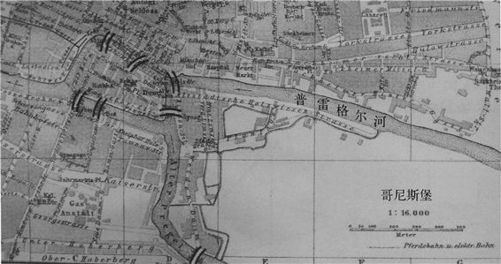
图3-8　柯尼斯堡的桥

哥尼斯堡的市民想知道能否有一条路线跨过每座桥一次，并且只跨过一次。1735年，著名的数学家莱昂哈德·欧拉着手解决这个问题，他画了一张图。

和“递棍儿”游戏中的孩子们不同的是，北区和岛区、岛区和南区之间都有多重的“友谊”，即桥梁。然而原理是一样的，欧拉证明，没有人能将每座桥跨过并且只跨过一次，因为四块地区都有奇数条桥梁与其他地区相连。

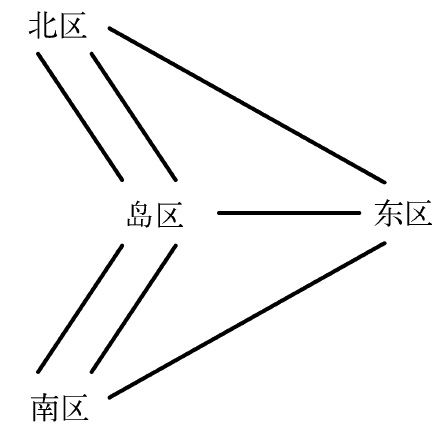
图3-9　欧拉的难题

因为源于欧拉和哥尼斯堡七桥难题，“递棍儿”游戏的成功完成方式叫做欧拉回路。玩的人比较多时，完成游戏的方式可能有很多种，但孩子们可以很容易地判断能不能玩成，只要数数有几个人的朋友个数是奇数就行了。

随着敌友国的孩子们渐渐长大，他们觉得“递棍儿”太简单了，没劲。于是他们稍微改了一下规则，新游戏起名为“递棍儿2”（真没创意）。修改后的规则如下：

• 只能给你的朋友递棍儿；
• 棍子必须且只能每个人经手一次，第一个递出棍子的人除外，因为棍子最终要还到他手里。

以下边这张朋友关系图为例，David把棍子递给Barbara，然后棍子依次经过Eric、Alex、Cathy，最终递回David手上。

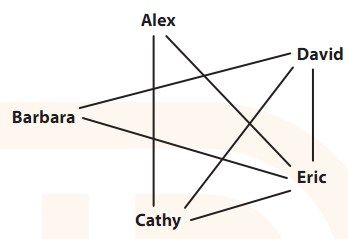
图3-10　可以完成的“递棍儿”

而在接下来这张图里，孩子们发现不可能完成“递棍儿2”。

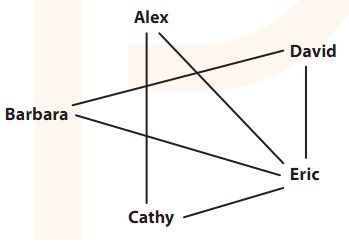
图3-11　不可能完成的“递棍儿”

由于规则变简单了，孩子们以为“递棍儿2”会更容易解决。但是当人数变得较多时，“递棍儿2”的难度陡然上升。1857年，数学家威廉·罗恩·哈密顿发明了一个叫Icosian的数学游戏。我们可以用“递棍儿2”来描述它的玩法，为了让图更简单，我们把每个人用名字的首字母代替。

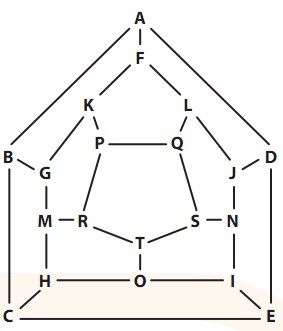
图3-12　Icosian难题

Icosian游戏来自正十二面体，即一个有十二个平面的球。

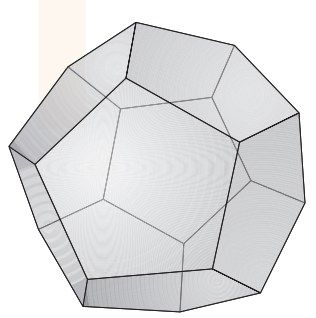
图3-13　十二面体

如果顶点代表敌友国的人，每条边代表一对朋友之间的关系，就会得到上面那张好友关系图。

为了纪念Icosian游戏的发明者，“递棍儿2”游戏的成功完成方式叫做哈密顿回路。