第 2 章　创建分类器

在这一章，我们将介绍以下主题：

  • 建立简单分类器（simple classifier）

  • 建立逻辑回归分类器（logistic regression classifier）

  • 建立朴素贝叶斯分类器（Naïve Bayes classifier）

  • 将数据集分割成训练集和测试集

  • 用交叉验证（cross-validation）检验模型准确性

  • 混淆矩阵（confusion matrix）可视化

  • 提取性能报告

  • 根据汽车特征评估质量

  • 生成验证曲线（validation curves）

  • 生成学习曲线（learning curves）

  • 估算收入阶层（income bracket）

2.1　简介

在机器学习领域中，分类是指利用数据的特性将其分成若干类型的过程。分类与上一章介绍的回归不同，回归的输出结果是实数。监督学习分类器就是用带标记的训练数据建立一个模型，然后对未知数据进行分类。

分类器可以是实现分类功能的任意算法，最简单的分类器就是简单的数学函数。在真实世界中，分类器可以是非常复杂的形式。在学习过程中，可以看到二元（binary）分类器，将数据分成两类，也可以看到多元（multiclass）分类器，将数据分成两个以上的类型。解决分类问题的数据手段都倾向于解决二元分类问题，可以通过不同的形式对其进行扩展，进而解决多元分类问题。

分类器准确性的估计是机器学习领域的重要内容。我们需要学会如何使用现有的数据获取新的思路（机器学习模型），然后把模型应用到真实世界中。在这一章里，我们将看到许多类似的主题。

2.2　建立简单分类器

本节学习如何用训练数据建立一个简单分类器。

2.2.1　详细步骤

(1)使用simple_classifier.py文件作为参考。假设你已经和上一章一样导入了numpy和matplotlib.pyplot程序包，那么需要创建一些样本数据：

  1. X = np.array([[3,1], [2,5], [1,8], [6,4], [5,2], [3,5], [4,7], [4,-1]])

(2) 为这些数据点分配一些标记：

  1. y = [0, 1, 1, 0, 0, 1, 1, 0]

(3) 因为只有两个类，所以y列表包含0和1。一般情况下，如果你有N个类，那么y的取值范围就是从0到N-1。接下来按照类型标记把样本数据分成两类：

  1. class_0 = np.array([X[i] for i in range(len(X)) if y[i]==0])
  2. class_1 = np.array([X[i] for i in range(len(X)) if y[i]==1])

(4) 为了对数据有个直观的认识，把图像画出来，如下所示：

  1. plt.figure()
  2. plt.scatter(class_0[:,0], class_0[:,1], color='black', marker='s')
  3. plt.scatter(class_1[:,0], class_1[:,1], color='black', marker='x')

这是一个散点图（scatterplot），用方块和叉表示两类数据。在前面的代码中，参数marker用来表示数据点的形状。用方块表示class_0的数据，用叉表示class_1的数据。运行代码，可以看到如图2-1所示的图形。

(5) 在之前的两行代码中，只是用变量X与y之间的映射关系创建了两个列表。如果要你直观地展示数据点的不同类型，在两类数据间画一条分割线，那么怎么实现呢？你只要用直线方程在两类数据之间画一条直线就可以了。下面看看如何实现：

  1. line_x = range(10)
  2. line_y = line_x

(6) 用数学公式y = x创建一条直线。代码如下所示：

  1. plt.figure()
  2. plt.scatter(class_0[:,0], class_0[:,1], color='black', marker='s')
  3. plt.scatter(class_1[:,0], class_1[:,1], color='black', marker='x')
  4. plt.plot(line_x, line_y, color='black', linewidth=3)
  5. plt.show()

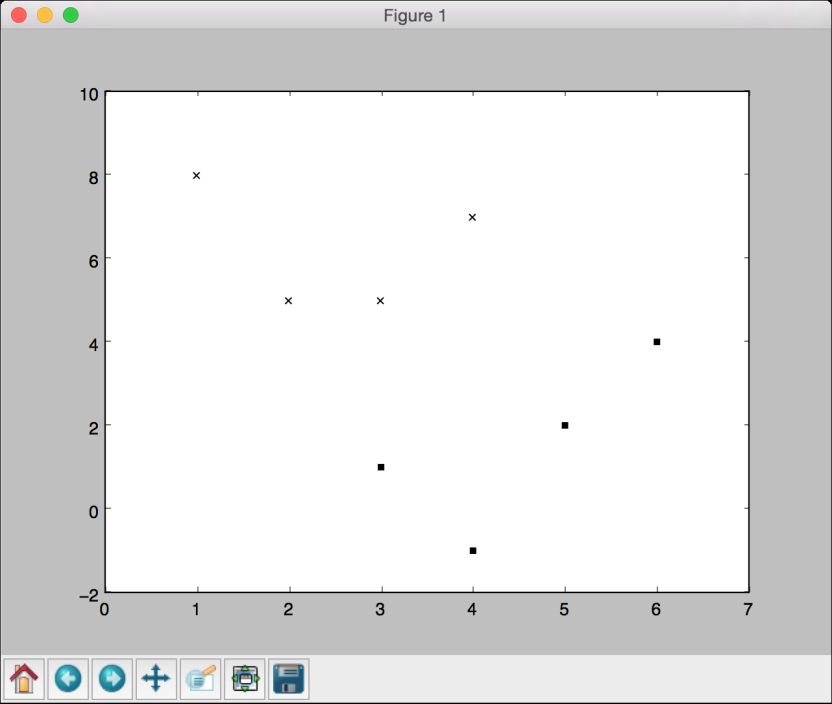
第 2 章　创建分类器 - 图1

图　2-1

(7) 运行代码，可以看到如图2-2所示的图形。

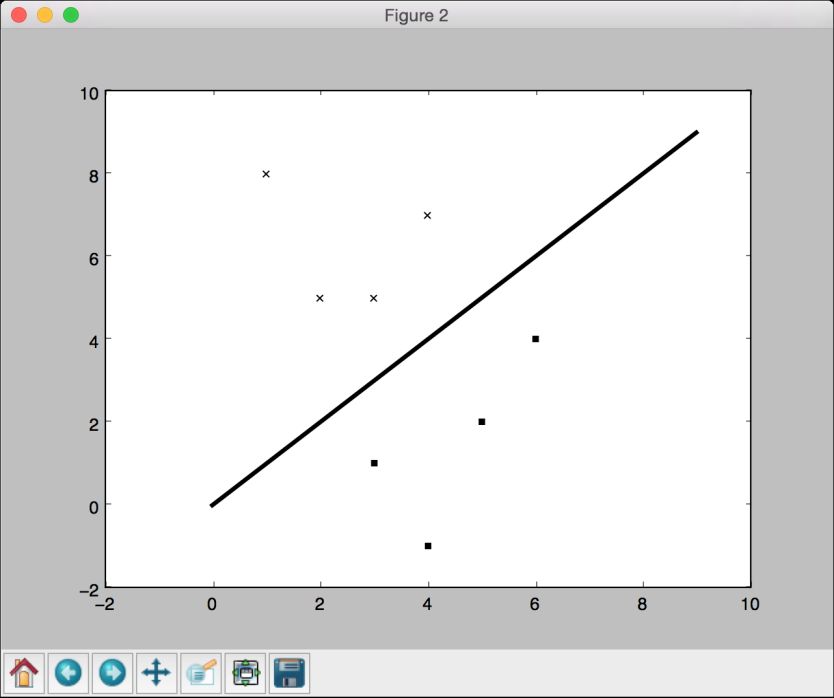
第 2 章　创建分类器 - 图2

图　2-2

2.2.2　更多内容

用以下规则建立了一个简单的分类器：如果输入点(a, b)的a大于或等于b，那么它属于类型class_0；反之，它属于class_1。如果对数据点逐个进行检查，你会发现每个数都是这样，这样你就建立了一个可以识别未知数据的线性分类器（linear classifier）。之所以称其为线性分类器，是因为分割线是一条直线。如果分割线是一条曲线，就是非线性分类器（nonlinear classifier）。

这样简单的分类器之所以可行，是因为数据点很少，可以直观地判断分割线。如果有几千个数据点呢？如何对分类过程进行一般化处理（generalize）呢？下一节将介绍这一主题。

2.3　建立逻辑回归分类器

虽然这里也出现了上一章介绍的回归这个词，但逻辑回归其实是一种分类方法。给定一组数据点，需要建立一个可以在类之间绘制线性边界的模型。逻辑回归就可以对训练数据派生的一组方程进行求解来提取边界。

详细步骤

(1) 下面看看用Python如何实现逻辑回归。我们使用logistic_regression.py文件作为参考。假设已经导入了需要使用的程序包，接下来创建一些带训练标记的样本数据：

  1. import numpy as np
  2. from sklearn import linear_model
  3. import matplotlib.pyplot as plt
  5. X = np.array([[4, 7], [3.5, 8], [3.1, 6.2], [0.5, 1], [1, 2],
  6. [1.2, 1.9], [6, 2], [5.7, 1.5], [5.4, 2.2]])
  7. y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2])

这里假设一共有3个类。

(2) 初始化一个逻辑回归分类器：

  1. classifier = linear_model.LogisticRegression(solver='liblinear', C=100)

前面的函数有一些输入参数需要设置，但是最重要的两个参数是solver和C。参数solver用于设置求解系统方程的算法类型，参数C表示正则化强度，数值越小，表示正则化强度越高。

(3) 接下来训练分类器：

  1. classifier.fit(X, y)

(4) 画出数据点和边界：

  1. plot_classifier(classifier, X, y)

需要定义如下画图函数：

  1. def plot_classifier(classifier, X, y):
  2.     # 定义图形的取值范围
  3.     x_min, x_max = min(X[:, 0]) - 1.0, max(X[:, 0]) + 1.0
  4.     y_min, y_max = min(X[:, 1]) - 1.0, max(X[:, 1]) + 1.0

预测值表示我们在图形中想要使用的数值范围，通常是从最小值到最大值。我们增加了一些余量（buffer），例如上面代码中的1.0。

(5) 为了画出边界，还需要利用一组网格（grid）数据求出方程的值，然后把边界画出来。下面继续定义网格：

  1.     # 设置网格数据的步长
  2.     step_size = 0.01
  4.     # 定义网格
  5.     x_values, y_values = np.meshgrid(np.arange(x_min, x_max, step_size), np.arange(y_min, y_max, step_size))

变量x_values和y_values包含求解方程数值的网格点。

(6) 计算出分类器对所有数据点的分类结果：

  1.     # 计算分类器输出结果
  2.     mesh_output = classifier.predict(np.c_[x_values.ravel(), y_values.ravel()])
  4.     # 数组维度变形
  5.     mesh_output = mesh_output.reshape(x_values.shape)

(7) 用彩色区域画出各个类型的边界：

  1.     # 用彩图画出分类结果
  2.     plt.figure()
  4.     # 选择配色方案
  5.     plt.pcolormesh(x_values, y_values, mesh_output, cmap=plt.cm.gray)

这基本算是一个三维画图器，既可以画二维数据点，又可以用色彩清单（color scheme）表示不同区域的相关属性。你可以在http://matplotlib.org/examples/color/colormaps_reference.html 找到所有的色彩清单。

(8) 接下来再把训练数据点画在图上：

  1.     plt.scatter(X[:, 0], X[:, 1], c=y, s=80, edgecolors='black', linewidth=1, cmap=plt.cm.Paired)
  3.     # 设置图形的取值范围
  4.     plt.xlim(x_values.min(), x_values.max())
  5.     plt.ylim(y_values.min(), y_values.max())
  7.     # 设置X轴与Y轴
  8.     plt.xticks((np.arange(int(min(X[:, 0])-1), int(max(X[:, 0])+1), 1.0)))
  9.     plt.yticks((np.arange(int(min(X[:, 1])-1), int(max(X[:, 1])+1), 1.0)))
  11.     plt.show()

其中，plt.scatter把数据点画在二维图上。X[:, 0]表示0轴（X轴）的坐标值，X[:, 1]表示1轴（Y轴）的坐标值。c=y表示颜色的使用顺序。用目标标记映射cmap的颜色表。我们肯定希望不同的标记使用不同的颜色，因此，用y作为映射。坐标轴的取值范围由plt.xlim和plt.ylim确定。为了标记坐标轴的数值，需要使用plt.xticks和plt.yticks。在坐标轴上标出坐标值，就可以直观地看出数据点的位置。在前面的代码中，我们希望坐标轴的最大值与最小值之前的刻度是单位刻度，还希望这些刻度值是整数，因此用int()函数对最值取整。

(9) 运行代码，就可以看到如图2-3所示的输出结果。

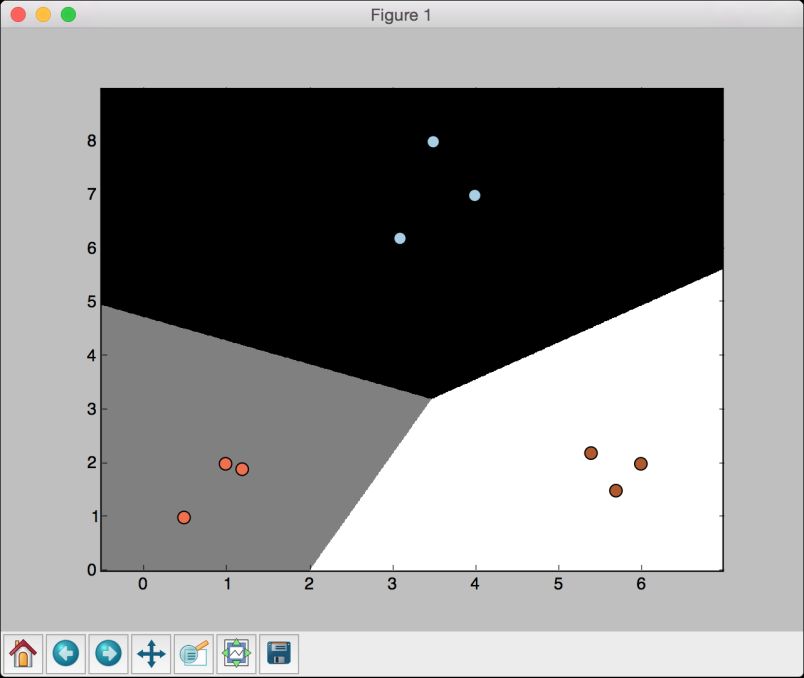
第 2 章　创建分类器 - 图3

图　2-3

(10) 下面看看参数C对模型的影响。参数C表示对分类错误（misclassification）的惩罚值（penalty）。如果把参数C设置为1.0，会得到如图2-4所示的结果。

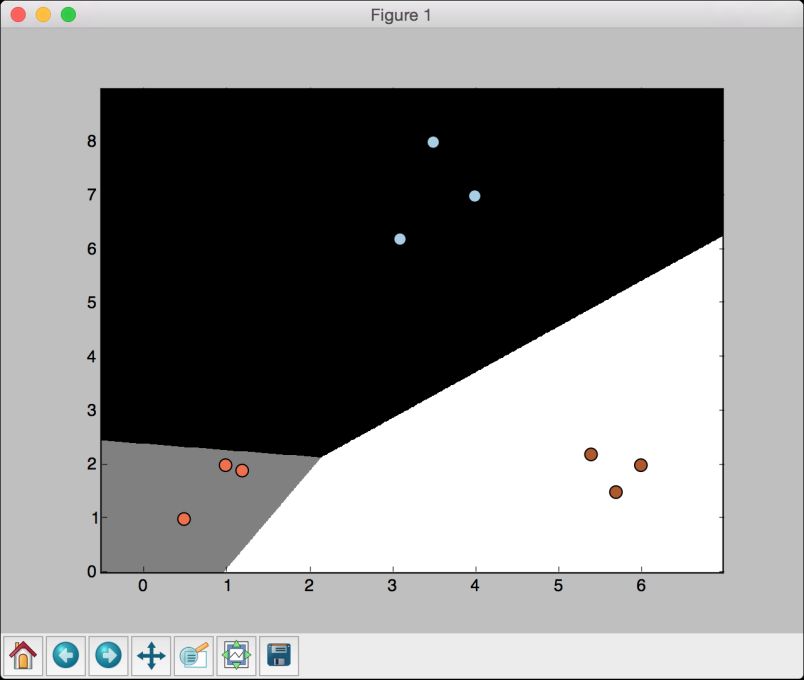
第 2 章　创建分类器 - 图4

图　2-4

(11) 如果把参数C设置为10000，会得到如图2-5所示的结果。

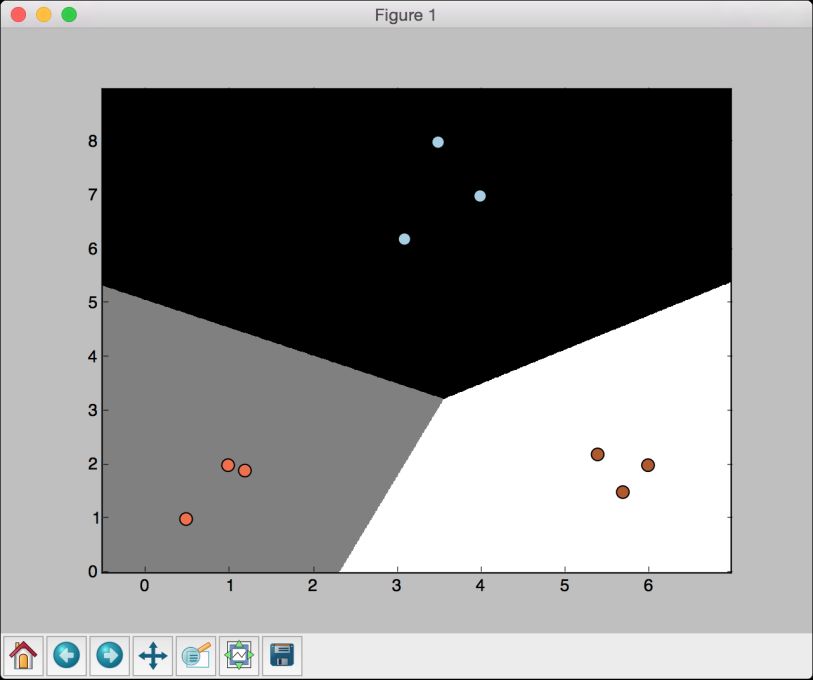
第 2 章　创建分类器 - 图5

图　2-5

随着参数C的不断增大，分类错误的惩罚值越高。因此，各个类型的边界更优。

2.4　建立朴素贝叶斯分类器

朴素贝叶斯分类器是用贝叶斯定理进行建模的监督学习分类器。下面看看如何建立一个朴素贝叶斯分类器。

详细步骤

(1) 我们使用naive_bayes.py文件作为参考。首先导入两个程序包：

  1. from sklearn.naive_bayes import GaussianNB
  2. from logistic_regression import plot_classifier

(2) 下载的示例代码中有一个data_multivar.txt文件，里面包含了将要使用的数据，每一行数据都是由逗号分隔符分割的数值。从文件中加载数据：

  1. input_file = 'data_multivar.txt'
  3. X = []
  4. y = []
  5. with open(input_file, 'r') as f:
  6.     for line in f.readlines():
  7.         data = [float(x) for x in line.split(',')]
  8.         X.append(data[:-1])
  9.         y.append(data[-1])
  11. X = np.array(X)
  12. y = np.array(y)

我们已经把输入数据和标记分别加载到变量X和y中了。

(3) 下面建立一个朴素贝叶斯分类器：

  1. classifier_gaussiannb = GaussianNB()
  2. classifier_gaussiannb.fit(X, y)
  3. y_pred = classifier_gaussiannb.predict(X)

GaussianNB函数指定了正态分布朴素贝叶斯模型（Gaussian Naive Bayes model）。

(4) 接下来计算分类器的准确性：

  1. accuracy = 100.0 * (y == y_pred).sum() / X.shape[0]
  2. print "Accuracy of the classifier =", round(accuracy, 2), "%"

(5) 画出数据点和边界：

  1. plot_classifier(classifier_gaussiannb, X, y)

可以看到如图2-6所示的图形。

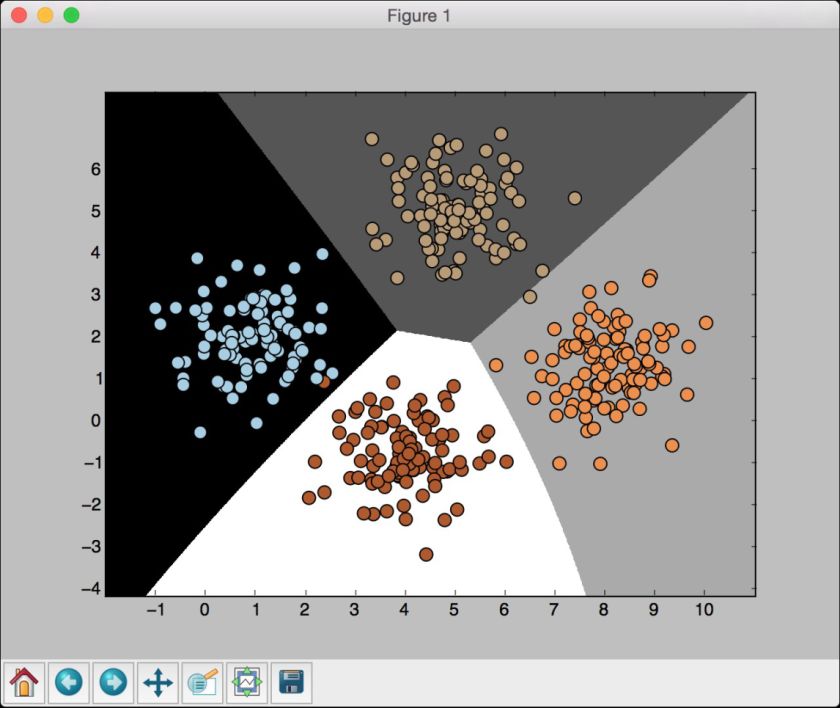
第 2 章　创建分类器 - 图6

图　2-6

从图2-6中可以发现，这里的边界没有严格地区分所有数据点。在前面这个例子中，我们是对所有的数据进行训练。机器学习的一条最佳实践是用没有重叠（nonoverlapping）的数据进行训练和测试。理想情况下，需要一些尚未使用的数据进行测试，可以方便准确地评估模型在未知数据上的执行情况。scikit-learn有一个方法可以非常好地解决这个问题，我们将在下一节介绍它。

2.5　将数据集分割成训练集和测试集

本节一起来看看如何将数据合理地分割成训练数据集和测试数据集。

详细步骤

(1) 增加下面的代码片段到上一节的Python文件中：

  1. from sklearn import cross_validation
  3. X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25, random_state=5)
  5. classifier_gaussiannb_new = GaussianNB()
  6. classifier_gaussiannb_new.fit(X_train, y_train)

这里，我们把参数test_size设置成0.25，表示分配了25%的数据给测试数据集。剩下75%的数据将用于训练数据集。

(2) 用分类器对测试数据进行测试：

  1. y_test_pred = classifier_gaussiannb_new.predict(X_test)

(3) 计算分类器的准确性：

  1. accuracy = 100.0 * (y_test == y_test_pred).sum() / X_test.shape[0]
  2. print "Accuracy of the classifier =", round(accuracy, 2), "%"

(4) 画出测试数据的数据点及其边界：

  1. plot_classifier(classifier_gaussiannb_new, X_test, y_test)

(5) 可以看到如图2-7所示的图形。

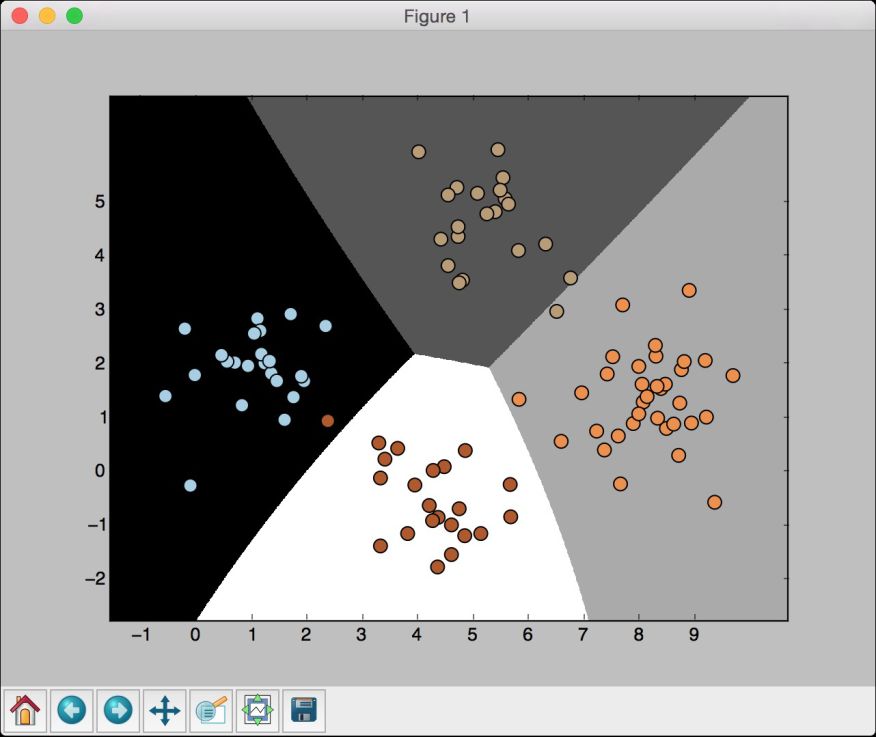
第 2 章　创建分类器 - 图7

图　2-7

2.6　用交叉验证检验模型准确性

交叉验证是机器学习的重要概念。在上一节中，我们把数据分成了训练数据集和测试数据集。然而，为了能够让模型更加稳定，还需要用数据集的不同子集进行反复的验证。如果只是对特定的子集进行微调，最终可能会过度拟合（overfitting）模型。过度拟合是指模型在已知数据集上拟合得超级好，但是一遇到未知数据就挂了。我们真正想要的，是让机器学习模型能够适用于未知数据。

2.6.1　准备工作

介绍如何实现交叉验证之前，先讨论一下性能指标。当处理机器学习模型时，通常关心3个指标：精度（precision）、召回率（recall）和F1得分（F1 score）。可以用参数评分标准（parameter scoring）获得各项指标的得分。精度是指被分类器正确分类的样本数量占分类器总分类样本数量的百分比（分类器分类结果中，有一些样本分错了）。召回率是指被应正确分类的样本数量占某分类总样本数量的百分比（有一些样本属于某分类，但分类器却没有分出来）。

假设数据集有100个样本，其中有82个样本是我们感兴趣的，现在想用分类器选出这82个样本。最终，分类器选出了73个样本，它认为都是我们感兴趣的。在这73个样本中，其实只有65个样本是我们感兴趣的，剩下的8个样本我们不感兴趣，是分类器分错了。可以如下方法计算分类器的精度：

  • 分类正确的样本数量 = 65

  • 总分类样本数量 = 73

  • 精度 = 65 / 73 = 89.04%

召回率的计算过程如下：

  • 数据集中我们感兴趣的样本数量 = 82

  • 分类正确的样本数量 = 65

  • 召回率 = 65 / 82 = 79.26%

一个给力的机器学习模型需要同时具备良好的精度和召回率。这两个指标是二律背反的，一个指标达到100%，那么另一个指标就会非常差！我们需要保持两个指标能够同时处于合理高度。为了量化两个指标的均衡性，引入了F1得分指标，是精度和召回率的合成指标，实际上是精度和召回率的调和均值（harmonic mean）：

F1 得分＝2×精度×召回率 / (精度＋召回率)

上面示例中F1得分的计算过程如下：

F1 得分＝2×0.89×0.79 / (0.89＋0.79)＝0.8370

2.6.2　详细步骤

(1) 下面看看如何实现交叉验证，并提取性能指标。首先计算精度：

  1. num_validations = 5
  2. accuracy = cross_validation.cross_val_score(classifier_gaussiannb,
  3.         X, y,scoring='accuracy', cv=num_validations)
  4. print "Accuracy: " + str(round(100*accuracy.mean(), 2)) + "%"

(2) 用前面的方程分别计算精度、召回率和F1得分：

  1. f1 = cross_validation.cross_val_score(classifier_gaussiannb,
  2.         X, y, scoring='f1_weighted', cv=num_validations)
  3. print "F1: " + str(round(100*f1.mean(), 2)) + "%"
  5. precision = cross_validation.cross_val_score(classifier_ gaussiannb,
  6.         X, y, scoring='precision_weighted', cv=num_validations)
  7. print "Precision: " + str(round(100*precision.mean(), 2)) + "%"
  9. recall = cross_validation.cross_val_score(classifier_gaussiannb,
  10.         X, y, scoring='recall_weighted', cv=num_validations)
  11. print "Recall: " + str(round(100*recall.mean(), 2)) + "%"

2.7　混淆矩阵可视化

混淆矩阵（confusion matrix）是理解分类模型性能的数据表，它有助于我们理解如何把测试数据分成不同的类。当想对算法进行调优时，就需要在对算法做出改变之前了解数据的错误分类情况。有些分类效果比其他分类效果更差，混淆矩阵可以帮助我们理解这些问题。先看看如图2-8所示的混淆矩阵。

{%}

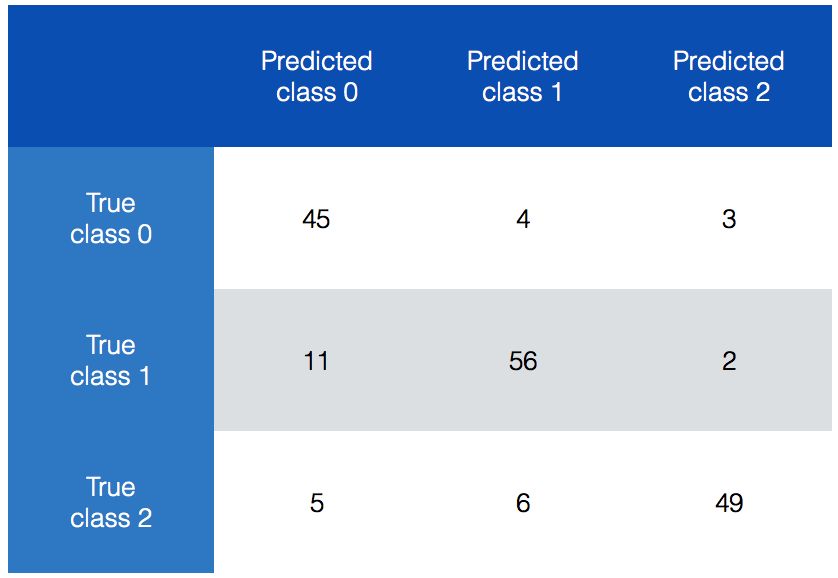
图　2-8

在图2-8中，我们可以看出不同类型的分类数据。理想情况下，我们希望矩阵非对角线元素都是0，这是最完美的分类结果。先看看class 0，一共52个样本属于class 0。如果对第一行数据求和，总数就是52。但是现在，只有45个样本被正确地预测出来，分类器说另外4个样本属于class 1，还有3个样本属于class 2。用同样的思路分析另外两行数据，有意思的是，class 1里面有11个样本被错误地预测成了class 0，占到了class 1总数的16%。这就是模型需要优化的切入点。

详细步骤

(1) 我们用confusion_matrix.py文件作为参考。首先看看如何从数据中提取混淆矩阵：

  1. from sklearn.metrics import confusion_matrix
  2. y_true = [1, 0, 0, 2, 1, 0, 3, 3, 3]
  3. y_pred = [1, 1, 0, 2, 1, 0, 1, 3, 3]
  4. confusion_mat = confusion_matrix(y_true, y_pred)
  5. plot_confusion_matrix(confusion_mat)

这里用了一些样本数据，一共有4种类型，取值范围是0~3，也列出了预测的标记类型。用confusion_matrix方法提取混淆矩阵，然后把它画出来。

(2) 继续定义混淆矩阵的画图函数：

  1. # 显示混淆矩阵
  2. def plot_confusion_matrix(confusion_mat):
  3.     plt.imshow(confusion_mat, interpolation='nearest', cmap=plt.cm.Paired)
  4.     plt.title('Confusion matrix')
  5.     plt.colorbar()
  6.     tick_marks = np.arange(4)
  7.     plt.xticks(tick_marks, tick_marks)
  8.     plt.yticks(tick_marks, tick_marks)
  9.     plt.ylabel('True label')
  10.     plt.xlabel('Predicted label')
  11.     plt.show()

这里用imshow函数画混淆矩阵，其他函数都非常简单，只使用相关函数设置了图形的标题、颜色栏、刻度和标签。参数tick_marks的取值范围是0~3，因为数据集中有4个标记类型。np.arange函数会生成一个numpy数组。

(3) 运行代码，可以看到如图2-9所示的图形。

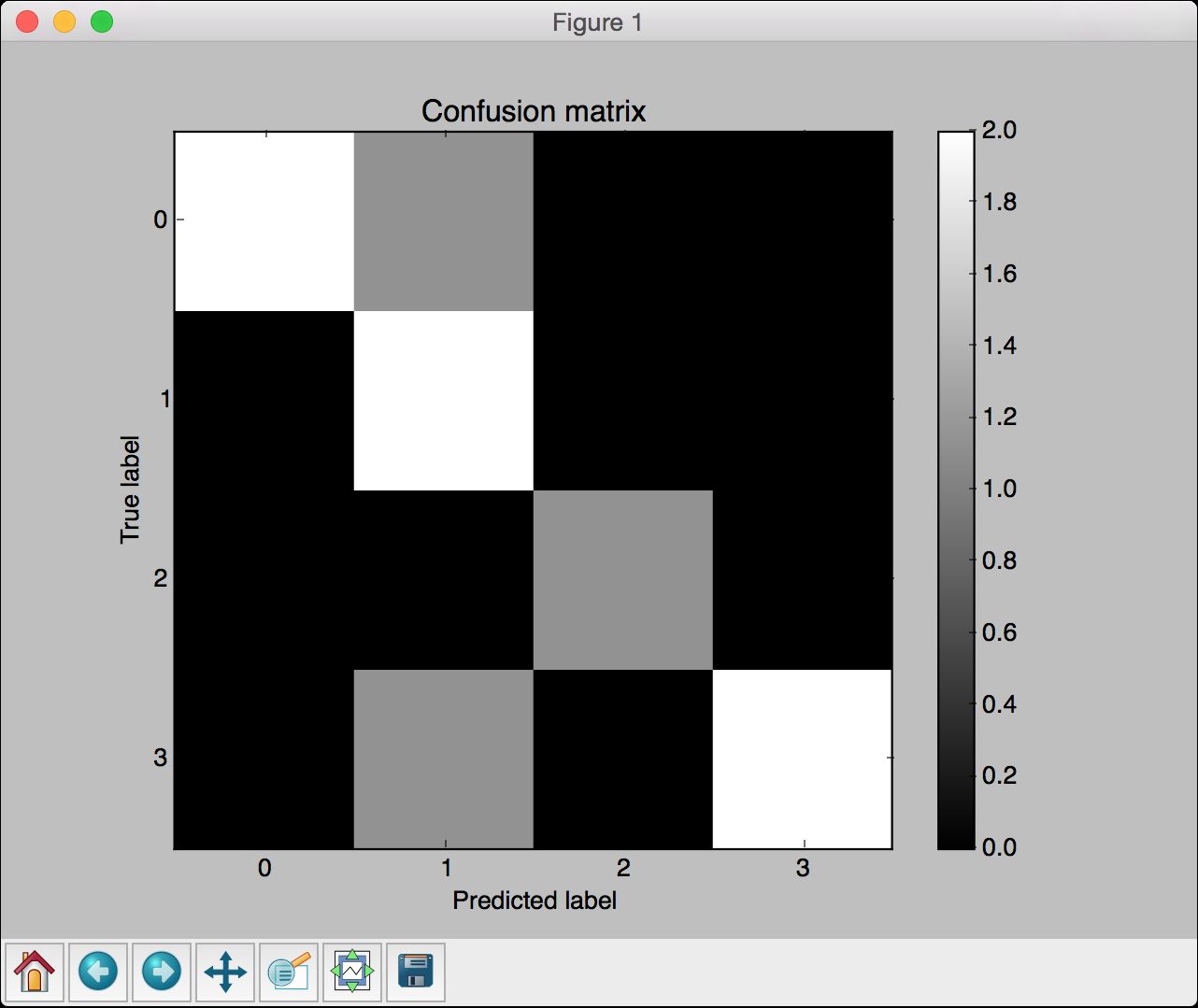
第 2 章　创建分类器 - 图9

图　2-9

从图2-9中可以看出，对角线的颜色很亮，我们希望它们越亮越好。黑色区域表示0。在非对角线的区域有一些灰色区域，表示分类错误的样本量。例如，当样本真实标记类型是0，而预测标记类型是1时，就像在第一行的第二格看到的那样。事实上，所有的错误分类都属于class-1，因为第二列有3个不为0的格子。这在图2-9中显示得一目了然。

2.8　提取性能报告

也可以直接用scikit-learn打印精度、召回率和F1得分。接下来看看如何实现。

详细步骤

(1) 在一个新的Python文件中加入下面的代码：

  1. from sklearn.metrics import classification_report
  2. y_true = [1, 0, 0, 2, 1, 0, 3, 3, 3]
  3. y_pred = [1, 1, 0, 2, 1, 0, 1, 3, 3]
  4. target_names = ['Class-0', 'Class-1', 'Class-2', 'Class-3']
  5. print(classification_report(y_true, y_pred, target_names=target_names))

(2) 运行代码，可以在命令行工具中看到如图2-10所示的结果。

{%}

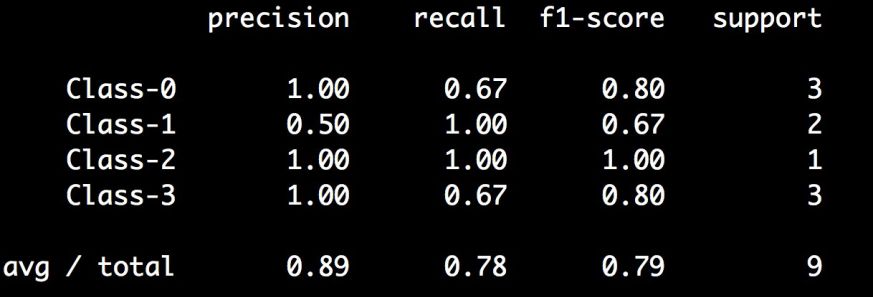
图　2-10

不需要单独计算各个指标，可以直接用这个函数从模型中提取所有统计值。

2.9　根据汽车特征评估质量

接下来看看如何用分类技术解决现实问题。我们将用一个包含汽车多种细节的数据集，例如车门数量、后备箱大小、维修成本等，来确定汽车的质量。分类的目的是把车辆的质量分成4种类型：不达标、达标、良好、优秀。

2.9.1　准备工作

你可以从https://archive.ics.uci.edu/ml/datasets/Car+Evaluation下载数据集。

你需要把数据集中的每个值看成是字符串。考虑数据集中的6个属性，其取值范围是这样的：

  • buying：取值范围是vhigh、high、med、low；

  • maint：取值范围是vhigh、high、med、low；

  • doors：取值范围是2、3、4、5等；

  • persons：取值范围是2、4等；

  • lug_boot：取值范围是small、med、big；

  • safety：取值范围是low、med、high。

考虑到每一行都包含字符串属性，需要假设所有特征都是字符串，并设置分类器。在上一章中，我们用随机森林建立过回归器，这里再用随机森林建立分类器。

2.9.2　详细步骤

(1) 参考car.py文件中的源代码。首先导入两个软件包：

  1. from sklearn import preprocessing
  2. from sklearn.ensemble import RandomForestClassifier

(2) 加载数据集：

  1. input_file = 'path/to/dataset/car.data.txt'
  3. # 读取数据
  4. X = []
  5. count = 0
  7. with open(input_file, 'r') as f:
  8.     for line in f.readlines():
  9.         data = line[:-1].split(',')
  10.         X.append(data)
  12. X = np.array(X)

每一行都包含由逗号分隔的单词列表。因此，我们解析输入文件，对每一行进行分割，然后将该列表附加到主数据。我们忽略每一行最后一个字符，因为那是一个换行符。由于Python程序包只能处理数值数据，所以需要把这些属性转换成程序包可以理解的形式。

(3) 在上一章中，我们介绍过标记编码。下面可以用这个技术把字符串转换成数值：

  1. # 将字符串转化为数值
  2. label_encoder = []
  3. X_encoded = np.empty(X.shape)
  4. for i,item in enumerate(X[0]):
  5.     label_encoder.append(preprocessing.LabelEncoder())
  6.     X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])
  8. X = X_encoded[:, :-1].astype(int)
  9. y = X_encoded[:, -1].astype(int)

由于每个属性可以取有限数量的数值，所以可以用标记编码器将它们转换成数字。我们需要为不同的属性使用不同的标记编码器，例如，lug_boot属性可以取3个不同的值，需要建立一个懂得给这3个属性编码的标记编码器。每一行的最后一个值是类，将它赋值给变量y。

(4) 接下来训练分类器：

  1. # 建立随机森林分类器
  2. params = {'n_estimators': 200, 'max_depth': 8, 'random_state': 7}
  3. classifier = RandomForestClassifier(**params)
  4. classifier.fit(X, y)

你可以改变n_estimators和max_depth参数的值，观察它们如何改变分类器的准确性。我们将用一个标准化的方法处理参数选择问题。

(5) 下面进行交叉验证：

  1. # 交叉验证
  2. from sklearn import cross_validation
  4. accuracy = cross_validation.cross_val_score(classifier,
  5.         X, y, scoring='accuracy', cv=3)
  6. print "Accuracy of the classifier: " + str(round(100*accuracy. mean(), 2)) + "%"

一旦训练好分类器，我们就需要知道它是如何执行的。我们用三折交叉验证（three-fold cross-validation，把数据分3组，轮换着用其中两组数据验证分类器）来计算分类器的准确性。

(6) 建立分类器的主要目的就是要用它对孤立的和未知的数据进行分类。下面用分类器对一个单一数据点进行分类：

  1. # 对单一数据示例进行编码测试
  2. input_data = ['vhigh', 'vhigh', '2', '2', 'small', 'low']
  3. input_data_encoded = [-1] * len(input_data)
  4. for i,item in enumerate(input_data):
  5.     input_data_encoded[i] = int(label_encoder[i].transform(input_data[i]))
  7. input_data_encoded = np.array(input_data_encoded)

第一步是把数据转换成数值类型。需要使用之前训练分类器时使用的标记编码器，因为我们需要保持数据编码规则的前后一致。如果输入数据点里出现了未知数据，标记编码器就会出现异常，因为它不知道如何对这些数据进行编码。例如，如果你把列表中的第一个值vhigh改成abcd，那么标记编码器就不知道如何编码了，因为它不知道怎么处理这个字符串。这就像是错误检查，看看输入数据点是否有效。

(7) 现在可以预测出数据点的输出类型了：

  1. # 预测并打印特定数据点的输出
  2. output_class = classifier.predict(input_data_encoded)
  3. print "Output class:", label_encoder[-1].inverse_transform(output_class)[0]

我们用predict方法估计输出类型。如果输出被编码的输出标记，那么它对我们没有任何意义。因此，用inverse_transform方法对标记进行解码，将它转换成原来的形式，然后打印输出类。

2.10　生成验证曲线

前面用随机森林建立了分类器，但是并不知道如何定义参数。本节来处理两个参数：n_estimators和max_depth参数。它们被称为超参数（hyperparameters），分类器的性能是由它们决定的。当改变超参数时，如果可以看到分类器性能的变化情况，那就再好不过了。这就是验证曲线的作用。这些曲线可以帮助理解每个超参数对训练得分的影响。基本上，我们只对感兴趣的超参数进行调整，其他参数可以保持不变。下面将通过可视化图片演示超参数的变化对训练得分的影响。

详细步骤

(1) 打开上一节的Python文件，加入以下代码：

  1. # 验证曲线
  3. from sklearn.learning_curve import validation_curve
  5. classifier = RandomForestClassifier(max_depth=4, random_state=7)
  6. parameter_grid = np.linspace(25, 200, 8).astype(int)
  7. train_scores, validation_scores = validation_curve(classifier, X, y, "n_estimators", parameter_grid, cv=5)
  8. print "\n##### VALIDATION CURVES #####"
  9. print "\nParam: n_estimators\nTraining scores:\n", train_scores
  10. print "\nParam: n_estimators\nValidation scores:\n", validation_ scores

在这个示例中，我们通过固定max_depth参数的值来定义分类器。我们想观察评估器数量对训练得分的影响，于是用parameter_grid定义了搜索空间。评估器数量会在25~200之间每隔8个数迭代一次，获得模型的训练得分和验证得分。

(2) 运行代码，可以在命令行工具中看到如图2-11所示的结果。

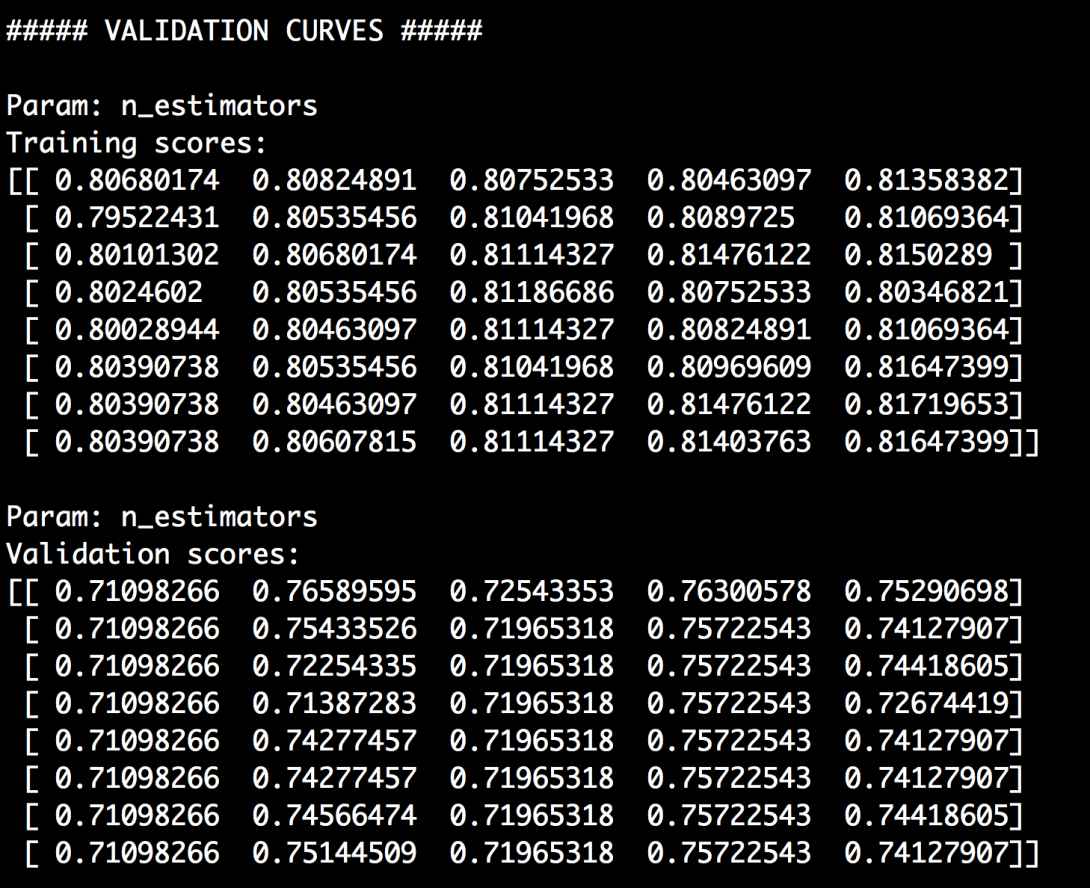
第 2 章　创建分类器 - 图11

图　2-11

(3) 把数据画成图形：

  1. # 画出曲线图
  2. plt.figure()
  3. plt.plot(parameter_grid, 100*np.average(train_scores, axis=1), color='black')
  4. plt.title('Training curve')
  5. plt.xlabel('Number of estimators')
  6. plt.ylabel('Accuracy')
  7. plt.show()

(4) 得到的图形如图2-12所示。

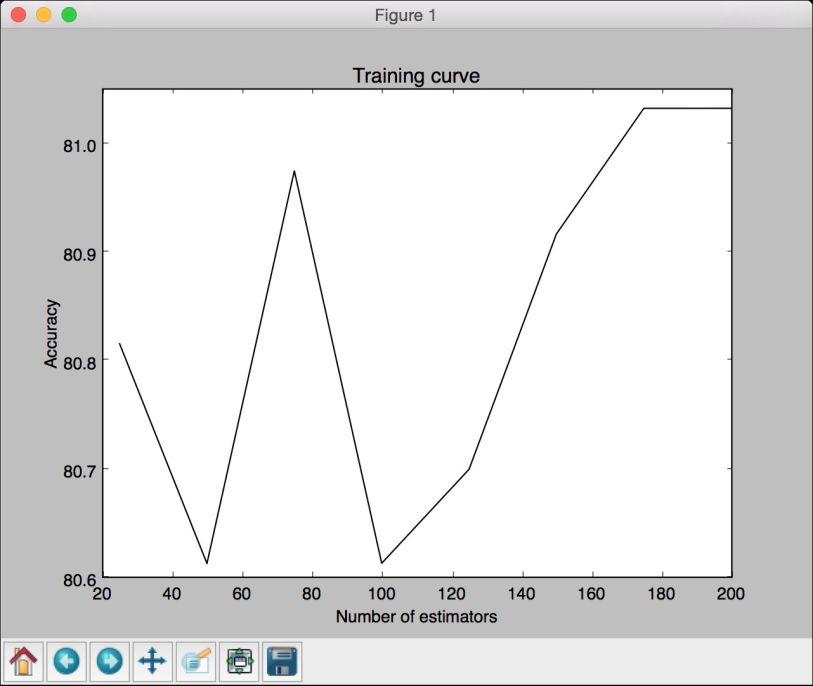
第 2 章　创建分类器 - 图12

图　2-12

(5) 用类似的方法对max_depth参数进行验证：

  1. classifier = RandomForestClassifier(n_estimators=20, random_ state=7)
  2. parameter_grid = np.linspace(2, 10, 5).astype(int)
  3. train_scores, valid_scores = validation_curve(classifier, X, y, "max_depth",
  4.         parameter_grid, cv=5)
  5. print "\nParam: max_depth\nTraining scores:\n", train_scores
  6. print "\nParam: max_depth\nValidation scores:\n", validation_ scores

我们把n_estimators参数固定为20，看看max_depth参数变化对性能的影响。命令行工具的输出结果如图2-13所示。

(6) 把数据画成图形：

  1. # 画出曲线图
  2. plt.figure()
  3. plt.plot(parameter_grid, 100*np.average(train_scores, axis=1), color='black')
  4. plt.title('Validation curve')
  5. plt.xlabel('Maximum depth of the tree')
  6. plt.ylabel('Accuracy')
  7. plt.show()

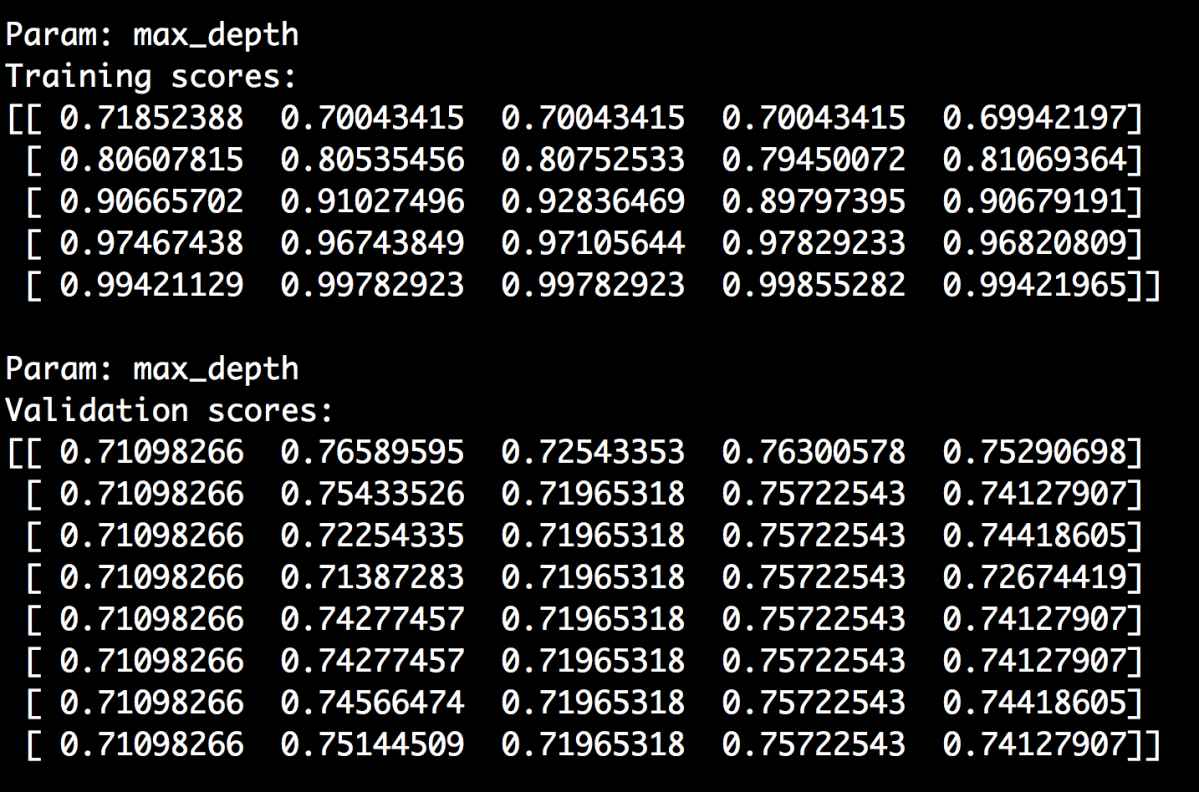
第 2 章　创建分类器 - 图13

图　2-13

(7) 运行代码，可以看到如图2-14所示的图形。

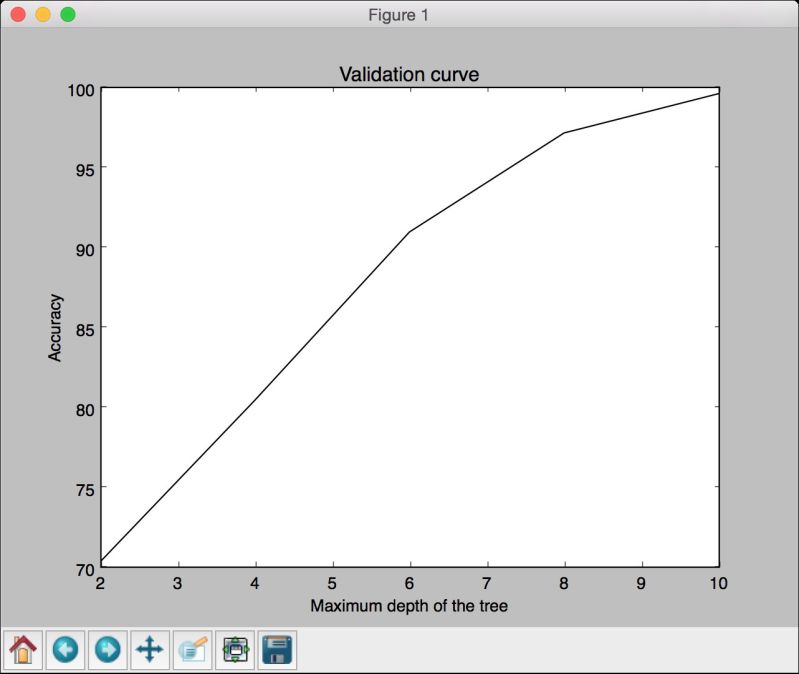
第 2 章　创建分类器 - 图14

图　2-14

2.11　生成学习曲线

学习曲线可以帮助我们理解训练数据集的大小对机器学习模型的影响。当遇到计算能力限制时，这一点非常有用。下面改变训练数据集的大小，把学习曲线画出来。

详细步骤

(1) 打开上一节的Python文件，加入以下代码：

  1. # 学习曲线
  3. from sklearn.learning_curve import learning_curve
  5. classifier = RandomForestClassifier(random_state=7)
  7. parameter_grid = np.array([200, 500, 800, 1100])
  8. train_sizes, train_scores, validation_scores = learning_ curve(classifier,
  9.         X, y, train_sizes=parameter_grid, cv=5)
  10. print "\n##### LEARNING CURVES #####"
  11. print "\nTraining scores:\n", train_scores
  12. print "\nValidation scores:\n", validation_scores

我们想分别用200、500、800、1100的训练数据集的大小测试模型的性能指标。我们把learning_curve方法中的cv参数设置为5，就是用五折交叉验证。

(2) 运行代码，可以在命令行工具中看到如图2-15所示的结果。

{%}

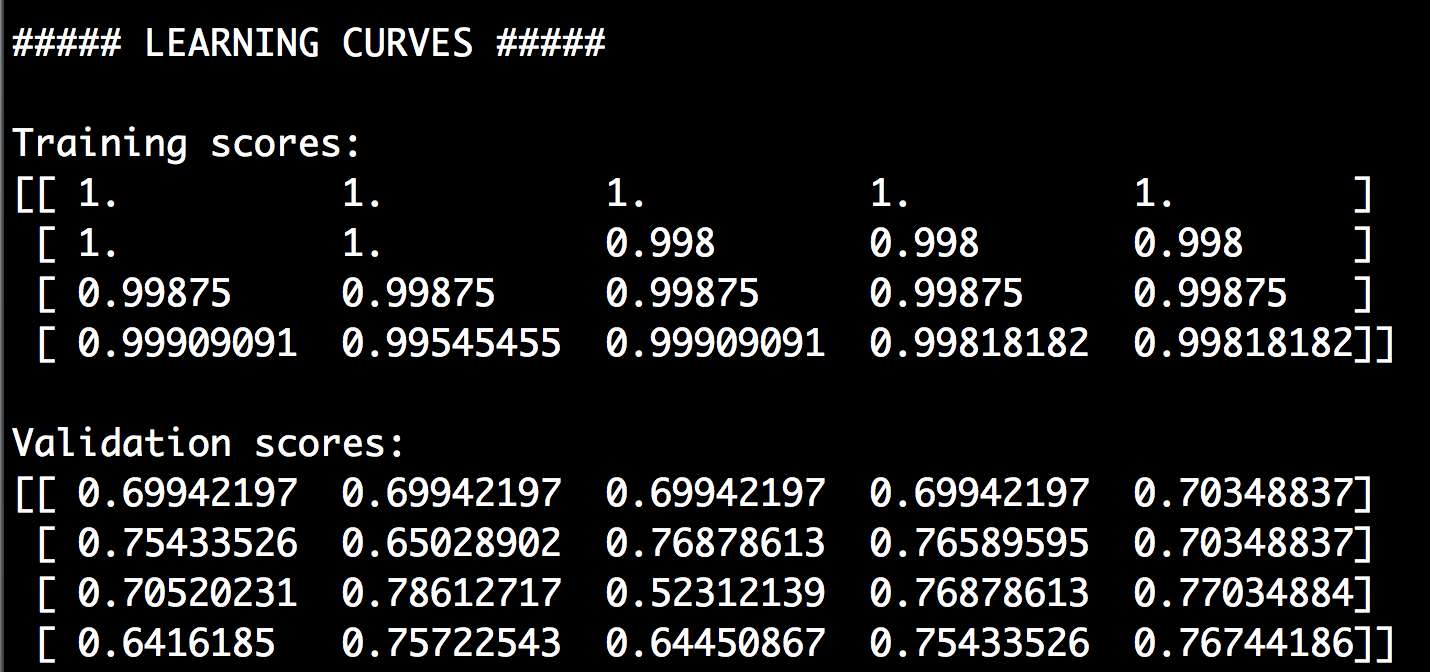
图　2-15

(3) 把数据画成图形：

  1. # 画出曲线图
  2. plt.figure()
  3. plt.plot(parameter_grid, 100*np.average(train_scores, axis=1), color='black')
  4. plt.title('Learning curve')
  5. plt.xlabel('Number of training samples')
  6. plt.ylabel('Accuracy')
  7. plt.show()

(4) 得到的图形如图2-16所示。

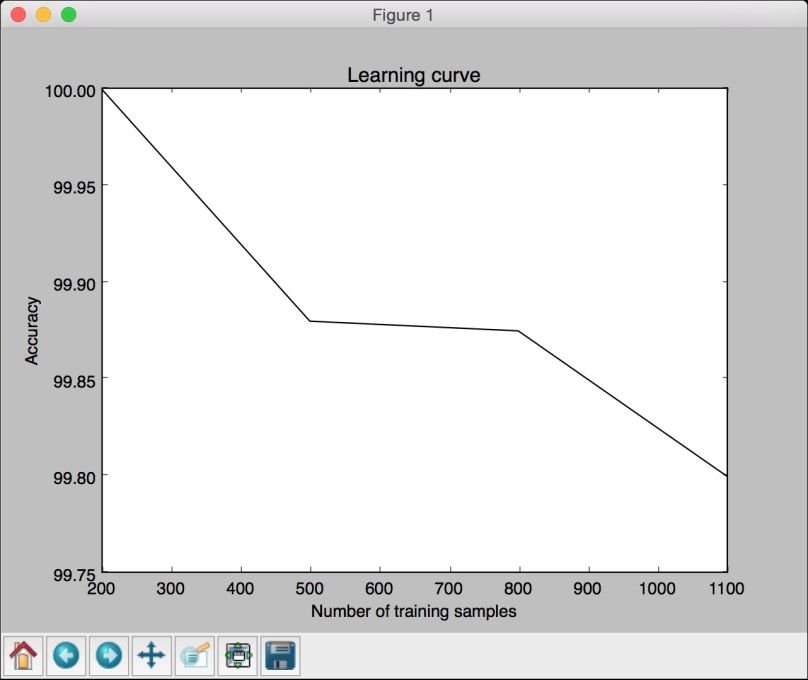
第 2 章　创建分类器 - 图16

图　2-16

虽然训练数据集的规模越小，仿佛训练准确性越高，但是它们很容易导致过度拟合。如果选择较大规模的训练数据集，就会消耗更多的资源。因此，训练数据集的规模选择也是一个需要结合计算能力进行综合考虑的问题。

2.12　估算收入阶层

本节将根据14个属性建立分类器评估一个人的收入等级。可能的输出类型是“高于50K”和“低于或等于50K”。这个数据集稍微有点复杂，里面的每个数据点都是数字和字符串的混合体。数值数据是有价值的，在这种情况下，不能用标记编码器进行编码。需要设计一套既可以处理数值数据，也可以处理非数值数据的系统。我们将用美国人口普查收入数据集中的数据： https://archive.ics.uci.edu/ml/datasets/Census+Income。

详细步骤

(1) 我们将用income.py文件作为参考，用朴素贝叶斯分类器解决问题。首先导入两个软件包：

  1. from sklearn import preprocessing
  2. from sklearn.naive_bayes import GaussianNB

(2) 加载数据集：

  1. input_file = 'path/to/adult.data.txt'
  3. # 读取数据
  4. X = []
  5. y = []
  6. count_lessthan50k = 0
  7. count_morethan50k = 0
  8. num_images_threshold = 10000

(3) 我们将使用数据集中的20 000个数据点——每种类型10 000个，保证初始类型没有偏差。在模型训练时，如果你的大部分数据点都属于一个类型，那么分类器就会倾向于这个类型。因此，最好使用每个类型数据点数量相等的数据进行训练：

  1. with open(input_file, 'r') as f:
  2.     for line in f.readlines():
  3.         if '?' in line:
  4.             continue
  6.         data = line[:-1].split(', ')
  8.         if data[-1] == '<=50K' and count_lessthan50k < num_images_threshold:
  9.             X.append(data)
  10.             count_lessthan50k = count_lessthan50k + 1
  12.         elif data[-1] == '>50K' and count_morethan50k < num_images_threshold:
  13.             X.append(data)
  14.             count_morethan50k = count_morethan50k + 1
  16.         if count_lessthan50k >= num_images_threshold and count_morethan50k >= num_images_threshold:
  17.             break
  19. X = np.array(X)

同样地，这也是一个带逗号分隔符的文件。我们还是像之前那样处理，把数据加载到变量X。

(4) 我们需要把字符串属性转换为数值数据，同时需要保留原有的数值数据：

  1. # 将字符串转换为数值数据
  2. label_encoder = []
  3. X_encoded = np.empty(X.shape)
  4. for i,item in enumerate(X[0]):
  5.     if item.isdigit():
  6.         X_encoded[:, i] = X[:, i]
  7.     else:
  8.         label_encoder.append(preprocessing.LabelEncoder())
  9.         X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])
  11. X = X_encoded[:, :-1].astype(int)
  12. y = X_encoded[:, -1].astype(int)

isdigit()函数帮助我们判断一个属性是不是数值数据。我们把字符串数据转换为数值数据，然后把所有的标记编码器保存在一个列表中，便于在后面处理未知数据时使用。

(5) 训练分类器：

  1. # 建立分类器
  2. classifier_gaussiannb = GaussianNB()
  3. classifier_gaussiannb.fit(X, y)

(6) 把数据分割成训练数据集和测试数据集，方便后面获取性能指标：

  1. # 交叉验证
  2. from sklearn import cross_validation
  4. X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25, random_state=5)
  5. classifier_gaussiannb = GaussianNB()
  6. classifier_gaussiannb.fit(X_train, y_train)
  7. y_test_pred = classifier_gaussiannb.predict(X_test)

(7) 提取性能指标：

  1. # 计算分类器的F1得分
  2. f1 = cross_validation.cross_val_score(classifier_gaussiannb,
  3.         X, y, scoring='f1_weighted', cv=5)
  4. print "F1 score: " + str(round(100*f1.mean(), 2)) + "%"

(8) 接下来看看如何为单一数据点分类。我们需要把数据点转换成分类器可以理解的形式：

  1. # 对单一数据示例进行编码测试
  2. input_data = ['39', 'State-gov', '77516', 'Bachelors', '13', 'Never-married', 'Adm-clerical', 'Not-in-family', 'White', 'Male', '2174', '0', '40', 'United-States']
  3. count = 0
  4. input_data_encoded = [-1] * len(input_data)
  5. for i,item in enumerate(input_data):
  6.     if item.isdigit():
  7.         input_data_encoded[i] = int(input_data[i])
  8.     else:
  9.         input_data_encoded[i] = int(label_encoder[count].transform(input_data[i]))
  10.         count = count + 1
  12. input_data_encoded = np.array(input_data_encoded)

(9) 这样就可以进行分类了：

  1. # 预测并打印特定数据点的输出结果
  2. output_class = classifier_gaussiannb.predict(input_data_encoded)
  3. print label_encoder[-1].inverse_transform(output_class)[0]

和之前的分类案例一样，我们用predict方法获取输出类型，然后用inverse_transform对标记进行解码，将它转换成原来的形式，然后在命令行工具中打印出来。