第 11 章　深度神经网络

在这一章，我们将介绍以下主题：

  • 创建一个感知器

  • 创建一个单层神经网络

  • 创建一个深度神经网络

  • 创建一个向量量化器

  • 为序列数据分析创建一个递归神经网络

  • 在光学字符识别数据库中将字符可视化

  • 用神经网络创建一个光学字符识别器

11.1　简介

人类的大脑很擅长于鉴别和识别物体，我们希望机器也可以做同样的事情。一个神经网络就是一个模仿人类大脑激发学习过程的框架。神经网络被用于从数据中识别隐藏的模式。正如所有的学习算法，神经网络处理的是数字。因此，如果想要实现处理现实世界中任何包含图像、文字、传感器等的任务，就必须将其转换成数值形式，然后将其输入到一个神经网络。我们可以用神经网络做分类、聚类、生成以及其他相关的任务。

神经网络由一层层神经元组成。这些神经元模拟人类大脑中的生物神经元。每一层都是一组独立的神经元，这些神经元与相邻层的神经元相连。输入层对应我们提供的输入数据，而输出层包括了我们期望的输出结果。输入层与输出层之间的层统称为隐藏层。如果设计的神经网络包括多个隐藏层，那么就能通过这些层的自我训练获得更大的精确度。

假设我们希望神经网络按照我们的要求来对数据进行分类。为了使神经网络完成相应的任务，需要提供带标签的训练数据。神经网络将通过优化成本函数来训练自己。我们不停地迭代，直到错误率下降到一定的阈值为止。

那么“深度”神经网络是什么？深度神经网络是由多个隐藏层组成的神经网络。一般来说，这就属于深度学习的范畴。深度学习用于研究这些神经网络，而这些神经网络由多个层次的多层结构组成。

你可以在http://pages.cs.wisc.edu/~bolo/shipyard/neural/local.html查看神经网络的教程。本章中将用到NeuroLab库。在接下来的学习之前，请确保你已经安装了这个库，安装指导可以参考https://pythonhosted.org/neurolab/install.html。接下来看看如何设计和开发这些神经网络。

11.2　创建一个感知器

让我们通过感知器开始神经网络之旅。感知器是一个单独的神经元，它负责执行所有的计算。这是一个非常简单的模型，但是它奠定了构建复杂神经网络的基础。该模型如图11-1所示。

{%}

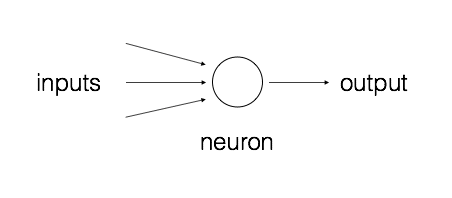
图　11-1

该神经元将多个输入用不同的权重系数融合起来，并加上偏差值来计算输出。这是一个简单的线性方程，它将输入值与感知器的输出关联起来。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import neurolab as nl
  3. import matplotlib.pyplot as plt

(2)定义一些输入数据及其对应的标签：

  1. # 定义输入数据
  2. data = np.array([[0.3, 0.2], [0.1, 0.4], [0.4, 0.6], [0.9, 0.5]])
  3. labels = np.array([[0], [0], [0], [1]])

(3) 将这些点画出，以查看这些点的布局：

  1. # 画出输入数据
  2. plt.figure()
  3. plt.scatter(data[:,0], data[:,1])
  4. plt.xlabel('X-axis')
  5. plt.ylabel('Y-axis')
  6. plt.title('Input data')

(4) 定义一个感知器perceptron，它有两个输入。该函数还需要限定输入数据的最大值和最小值：

  1. # 定义有两个输入的感知器，在感知器第一个参数的每个元素中指定参数的最大值和最小值
  2. perceptron = nl.net.newp([[0, 1],[0, 1]], 1)

(5) 接下来训练该感知器。epochs的数量指定了训练数据集需要完成的测试次数。show参数指定了显示训练过程的频率。lr参数指定了感知器的学习速度。学习速度是指学习算法在参数空间中搜索的步长。如果这个值太大，算法行进得会很快，但可能会错失最优值。而如果这个值太小，则该算法可以命中最优值，但是算法行进得会很慢，所以需要进行权衡。这里取0.01：

  1. # 训练感知器
  2. error = perceptron.train(data, labels, epochs=50, show=15, lr=0.01)

(6) 画出结果：

  1. # 画出结果
  2. plt.figure()
  3. plt.plot(error)
  4. plt.xlabel('Number of epochs')
  5. plt.ylabel('Training error')
  6. plt.grid()
  7. plt.title('Training error progress')
  9. plt.show()

(7) 全部代码已经在perceptron.py文件中给出。运行该代码，可以看到两幅图像。第一幅图像显示输入数据，如图11-2所示。

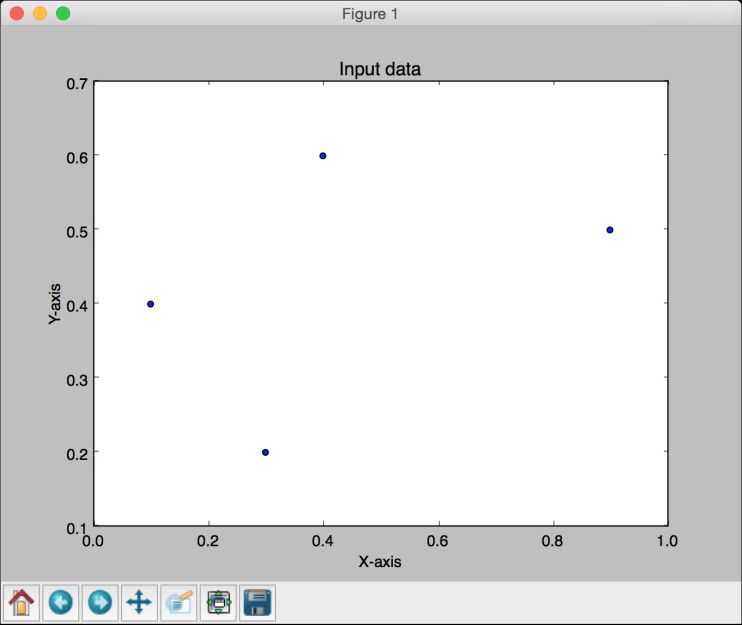
第 11 章　深度神经网络 - 图2

图　11-2

第二幅图像显示训练误差进程，如图11-3所示。

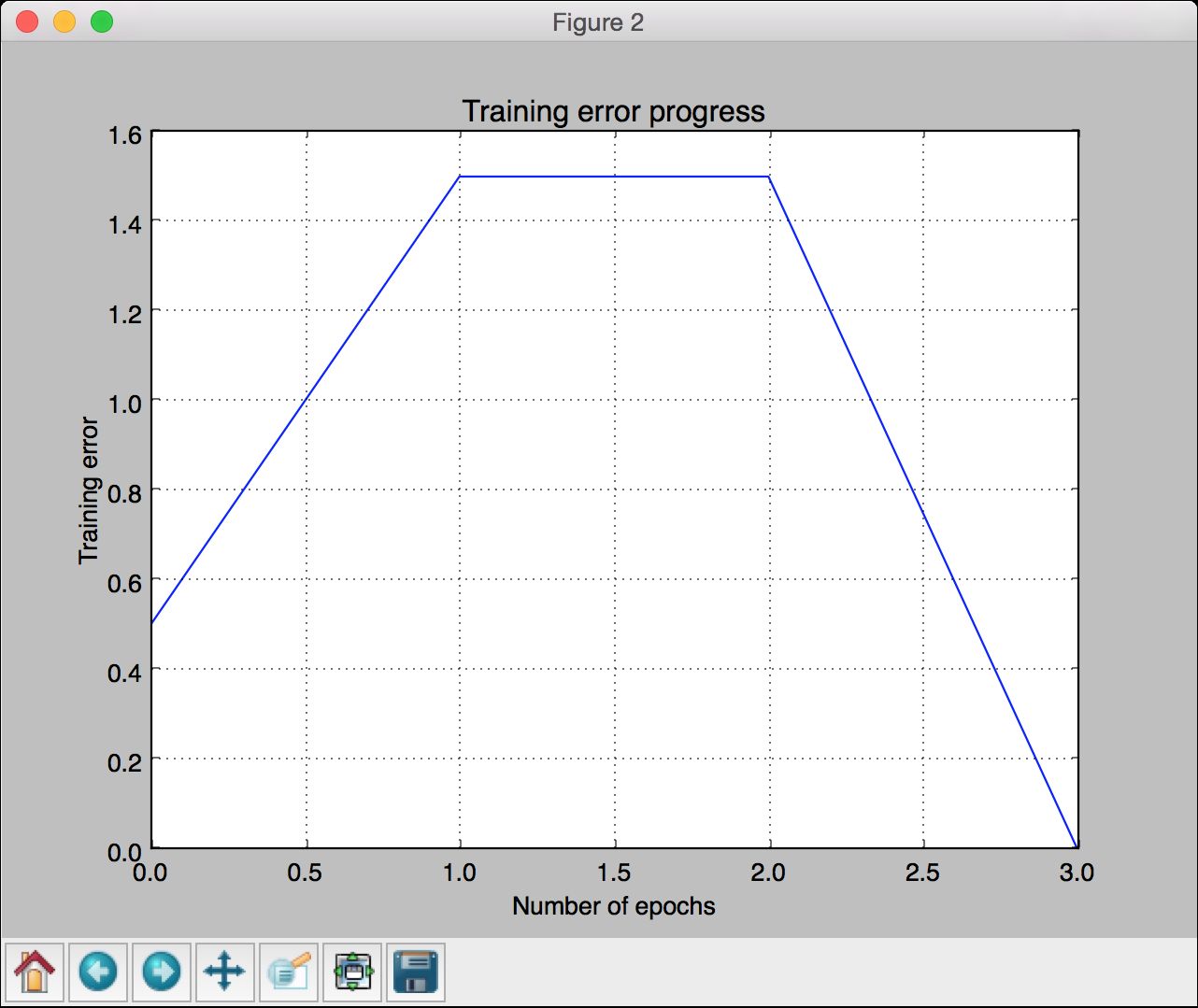
第 11 章　深度神经网络 - 图3

图　11-3

11.3　创建一个单层神经网络

知道如何创建一个感知器后，接下来创建一个单层神经网络。单层神经网络由一个层次中的多个神经元组成。总体上看，单层神经网络将会有一个输入层、一个隐藏层和一个输出层。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. import neurolab as nl

(2) 本例将会用到data_single_layer.txt文件中的数据。先加载这个文件：

  1. # 定义输入数据
  2. input_file = 'data_single_layer.txt'
  3. input_text = np.loadtxt(input_file)
  4. data = input_text[:, 0:2]
  5. labels = input_text[:, 2:]

(3) 画出输入数据：

  1. # 画出输入数据
  2. plt.figure()
  3. plt.scatter(data[:,0], data[:,1])
  4. plt.xlabel('X-axis')
  5. plt.ylabel('Y-axis')
  6. plt.title('Input data')

(4) 提取最小值和最大值：

  1. # 提取每个维度的最小值和最大值
  2. x_min, x_max = data[:,0].min(), data[:,0].max()
  3. y_min, y_max = data[:,1].min(), data[:,1].max()

(5) 定义一个单层神经网络，该神经网络的隐藏层包含两个神经元：

  1. # 定义一个单层神经网络，包含两个神经元；在感知器第一个参数的每个元素中指定参数的最大值和最小值
  2. single_layer_net = nl.net.newp([[x_min, x_max], [y_min, y_max]], 2)

(6) 通过50次迭代训练该神经网络：

  1. # 训练神经网络
  2. error = single_layer_net.train(data, labels, epochs=50, show=20, lr=0.01)

(7) 画出结果：

  1. # 画出结果
  2. plt.figure()
  3. plt.plot(error)
  4. plt.xlabel('Number of epochs')
  5. plt.ylabel('Training error')
  6. plt.title('Training error progress')
  7. plt.grid()
  9. plt.show()

(8) 用新的测试数据来测试神经网络：

  1. print single_layer_net.sim([[0.3, 4.5]])
  2. print single_layer_net.sim([[4.5, 0.5]])
  3. print single_layer_net.sim([[4.3, 8]])

(9) 全部代码已经在single_layer.py文件中给出。运行该代码，可以看到两幅图像。第一幅图像显示输入数据，如图11-4所示。

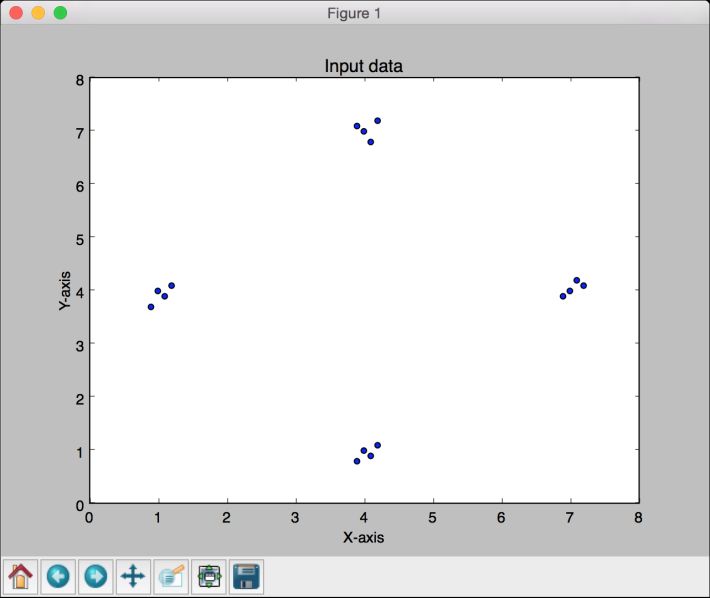
第 11 章　深度神经网络 - 图4

图　11-4

(10) 第二幅图像显示训练误差进程，如图11-5所示。

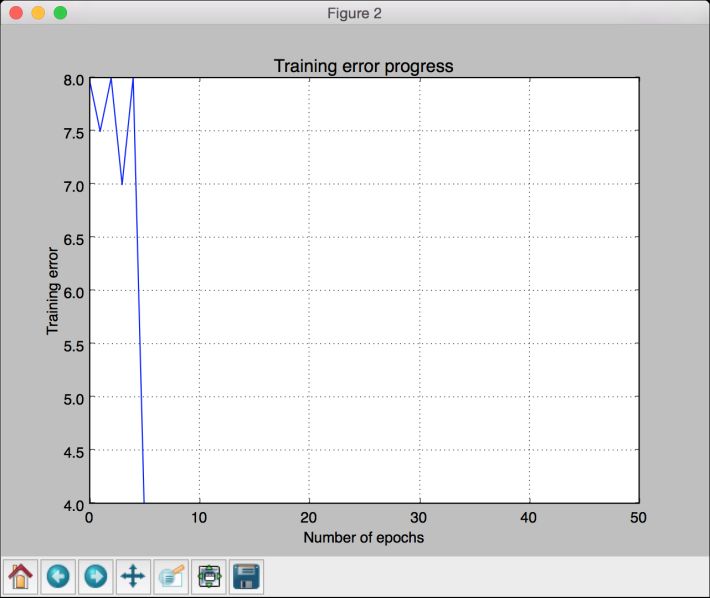
第 11 章　深度神经网络 - 图5

图　11-5

可以在命令行工具中看到如下输出结果，指示输入测试点所属的位置：

  1. [[ 0.   0.]]
  2. [[ 1.   0.]]
  3. [[ 1.   1.]]

可以基于标签来验证输出结果的准确性。

11.4　创建一个深度神经网络

接下来创建一个深度神经网络。一个深度神经网络由一个输入层、多个隐藏层和一个输出层组成。该模型如图11-6所示。

{%}

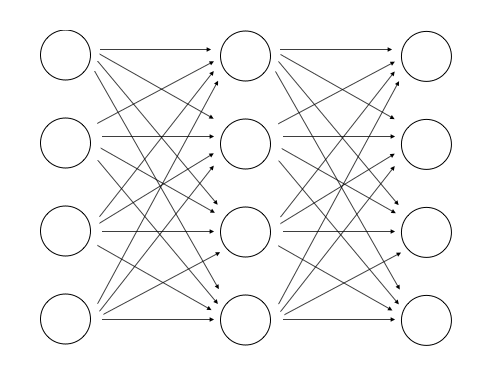
图　11-6

图11-6展示了一个多层神经网络，该神经网络包括一个输入层、多个隐藏层和一个输出层。在一个深度神经网络中，输入层和输出层之间有多个隐藏层。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import neurolab as nl
  2. import numpy as np
  3. import matplotlib.pyplot as plt

(2) 定义以下参数，用于生成训练数据：

  1. # 生成训练数据
  2. min_value = -12
  3. max_value = 12
  4. num_datapoints = 90

(3) 训练数据将由我们定义的一个函数组成，该函数将转换值。我们期望神经网络可以根据提供的输入数据和输出数据来学习这一点：

  1. x = np.linspace(min_value, max_value, num_datapoints)
  2. y = 2 * np.square(x) + 7
  3. y /= np.linalg.norm(y)

(4) 数组变形：

  1. data = x.reshape(num_datapoints, 1)
  2. labels = y.reshape(num_datapoints, 1)

(5) 画出输入数据：

  1. # 画出输入数据
  2. plt.figure()
  3. plt.scatter(data, labels)
  4. plt.xlabel('X-axis')
  5. plt.ylabel('Y-axis')
  6. plt.title('Input data')

(6) 定义一个深度神经网络，该神经网络包含两个隐藏层，每个隐藏层包含10个神经元：

  1. # 定义一个深度神经网络，带两个隐藏层；每个隐藏层由10个神经元组成，输出层由一个神经元组成
  2. multilayer_net = nl.net.newff([[min_value, max_value]], [10, 10, 1])

(7) 设置训练算法为梯度下降法（关于梯度下降法的介绍可参考https://spin.atomicobject.com/2014/06/24/gradient-descent-linear-regression）：

  1. # 设置训练算法为梯度下降法
  2. multilayer_net.trainf = nl.train.train_gd

(8) 训练网络：

  1. # 训练网络
  2. error = multilayer_net.train(data, labels, epochs=800, show=100, goal=0.01)

(9) 用训练数据运行该网络，查看其性能表现：

  1. # 用训练数据运行该网络，预测结果
  2. predicted_output = multilayer_net.sim(data)

(10) 画出训练误差结果：

  1. # 画出训练误差结果
  2. plt.figure()
  3. plt.plot(error)
  4. plt.xlabel('Number of epochs')
  5. plt.ylabel('Error')
  6. plt.title('Training error progress')

(11) 创建一组新的输入数据，并运行神经网络，查看其性能表现：

  1. # 画出预测结果
  2. x2 = np.linspace(min_value, max_value, num_datapoints * 2)
  3. y2 = multilayer_net.sim(x2.reshape(x2.size,1)).reshape(x2.size)
  4. y3 = predicted_output.reshape(num_datapoints)

(12) 画出输出结果：

  1. plt.figure()
  2. plt.plot(x2, y2, '-', x, y, '.', x, y3, 'p')
  3. plt.title('Ground truth vs predicted output')
  5. plt.show()

(13) 全部代码已经在deep_neural_network.py文件中给出。运行该代码，可以看到3幅图像。第一幅图像显示输入数据，如图11-7所示。

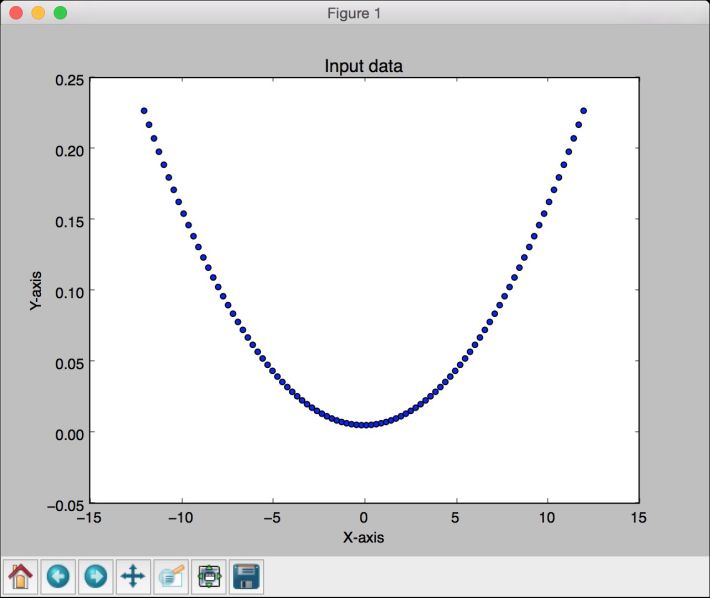
第 11 章　深度神经网络 - 图7

图　11-7

第二幅图像显示训练误差进程，如图11-8所示。

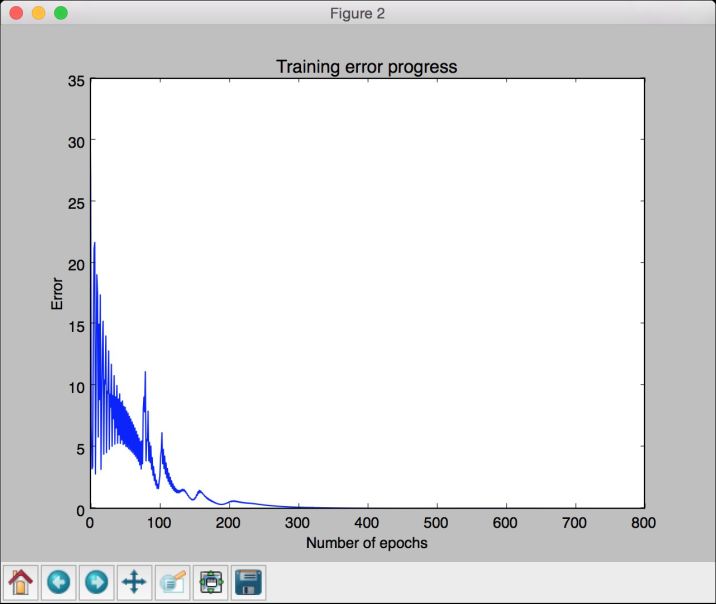
第 11 章　深度神经网络 - 图8

图　11-8

第三幅图像显示神经网络的输出，如图11-9所示。

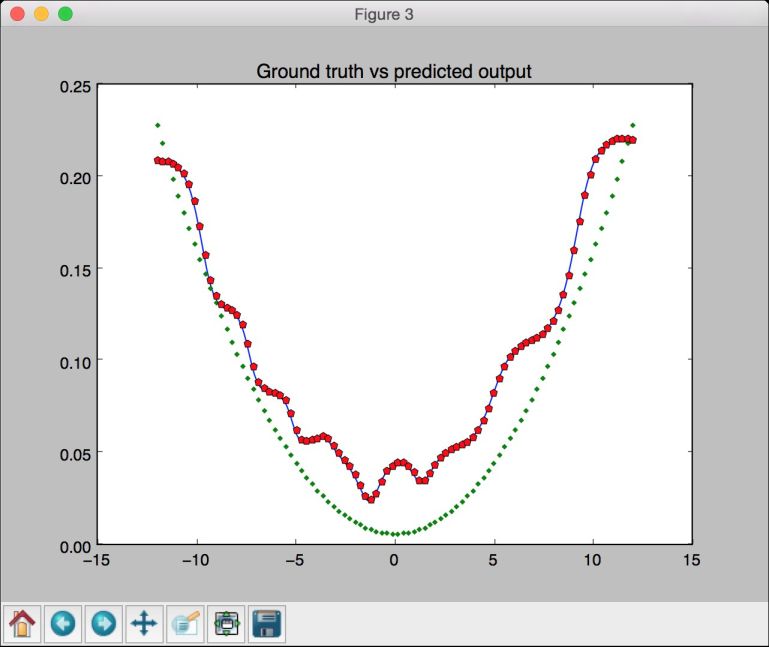
第 11 章　深度神经网络 - 图9

图　11-9

可以在命令行工具中看到如图11-10所示的显示结果。

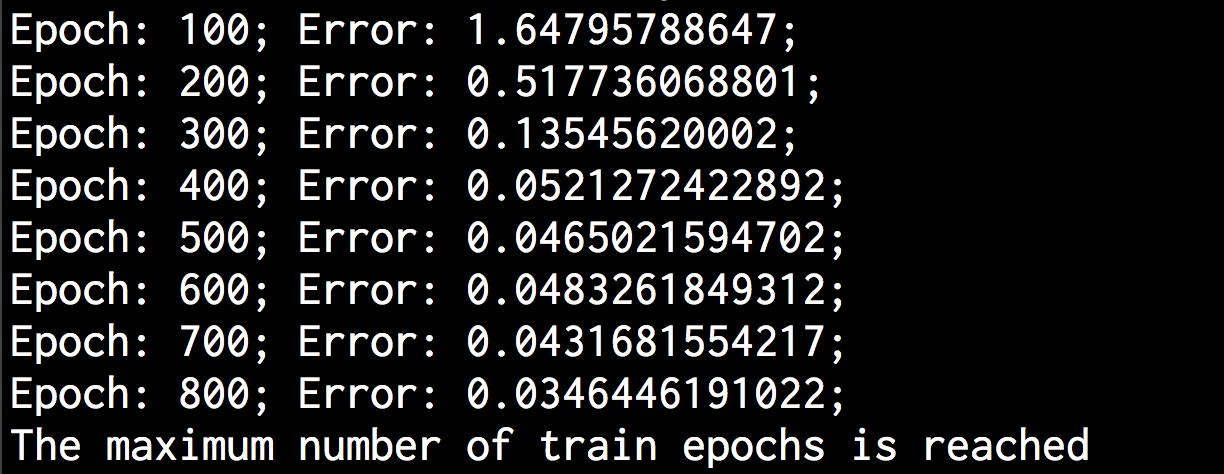
第 11 章　深度神经网络 - 图10

图　11-10

11.5　创建一个向量量化器

你也可以用神经网络来做向量量化。向量量化是N 维空间的“四舍五入”，广泛用于各个领域，如计算机视觉、自然语言处理和机器学习等。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. import neurolab as nl

(2) 从data_vq.txt文件加载输入数据：

  1. # 定义输入数据
  2. input_file = 'data_vq.txt'
  3. input_text = np.loadtxt(input_file)
  4. data = input_text[:, 0:2]
  5. labels = input_text[:, 2:]

(3) 定义一个两层的学习向量量化（Learning Vector Quantization，LVQ）神经网络。函数中最后一个参数的数组指定了每个输出的加权百分比（各加权百分比之和应为1）：

  1. # 定义一个两层神经网络：输入含10个神经元，输出含4个神经元
  2. net = nl.net.newlvq(nl.tool.minmax(data), 10, [0.25, 0.25, 0.25, 0.25])

(4) 训练LVQ神经网络：

  1. # 训练神经网络
  2. error = net.train(data, labels, epochs=100, goal=-1)

(5) 创建一个用于测试及可视化的网格点值：

  1. # 创建输入网格
  2. xx, yy = np.meshgrid(np.arange(0, 8, 0.2), np.arange(0, 8, 0.2))
  3. xx.shape = xx.size, 1
  4. yy.shape = yy.size, 1
  5. input_grid = np.concatenate((xx, yy), axis=1)

(6) 用这些网格点值评价该网络：

  1. # 用这些网格点值评价该网络
  2. output_grid = net.sim(input_grid)

(7) 在数据中定义4个类：

  1. # 定义4个类
  2. class1 = data[labels[:,0] == 1]
  3. class2 = data[labels[:,1] == 1]
  4. class3 = data[labels[:,2] == 1]
  5. class4 = data[labels[:,3] == 1]

(8) 为每个类定义网格：

  1. # 为4个类定义网格
  2. grid1 = input_grid[output_grid[:,0] == 1]
  3. grid2 = input_grid[output_grid[:,1] == 1]
  4. grid3 = input_grid[output_grid[:,2] == 1]
  5. grid4 = input_grid[output_grid[:,3] == 1]

(9) 画出输出结果：

  1. # 画出输出结果
  2. plt.plot(class1[:,0], class1[:,1], 'ko', class2[:,0], class2[:,1], 'ko',
  3.                 class3[:,0], class3[:,1], 'ko', class4[:,0], class4[:,1], 'ko')
  4. plt.plot(grid1[:,0], grid1[:,1], 'b.', grid2[:,0], grid2[:,1], 'gx',
  5.                 grid3[:,0], grid3[:,1], 'cs', grid4[:,0], grid4[:,1], 'ro')
  6. plt.axis([0, 8, 0, 8])
  7. plt.xlabel('X-axis')
  8. plt.ylabel('Y-axis')
  9. plt.title('Vector quantization using neural networks')
  11. plt.show()

(10) 全部代码已经在vector_quantization.py文件中给出。运行该代码，可以看到图像空间被分成不同区域，如图11-11所示。每个区域对应空间中向量量化区域列表中的一个。

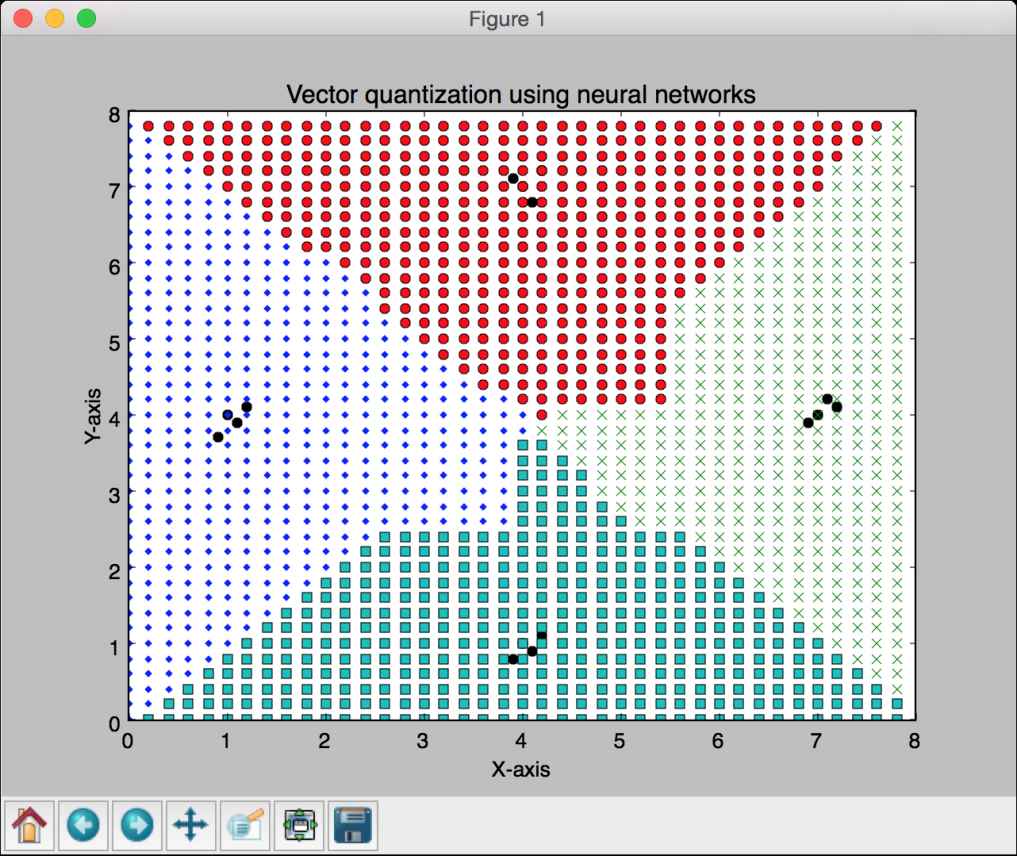
第 11 章　深度神经网络 - 图11

图　11-11

11.6　为序列数据分析创建一个递归神经网络

递归神经网络能较好地分析序列和时间序列数据。你可以在http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns看到更多关于递归神经网络的详细内容。在处理序列和时间序列数据时，不能简单地扩展通用模型。数据的时序相关性非常关键，构建模型时需要考虑到这一点。接下来看看如何创建递归神经网络。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. import neurolab as nl

(2) 定义一个函数，该函数利用输入参数创建一个波形：

  1. def create_waveform(num_points):
  2.     # 创建训练样本
  3.     data1 = 1  np.cos(np.arange(0, num_points))
  4.     data2 = 2  np.cos(np.arange(0, num_points))
  5.     data3 = 3  np.cos(np.arange(0, num_points))
  6.     data4 = 4  np.cos(np.arange(0, num_points))

(3) 为每个区间创建不同的振幅，以此来创建一个随机波形：

  1.     # 创建不同的振幅
  2.     amp1 = np.ones(num_points)
  3.     amp2 = 4 + np.zeros(num_points)
  4.     amp3 = 2 * np.ones(num_points)
  5.     amp4 = 0.5 + np.zeros(num_points)

(4) 将数组合并生成输出数组，其中数据对应输入，而振幅对应相应的标签：

  1.     data = np.array([data1, data2, data3, data4]).reshape(num_points * 4, 1)
  2.     amplitude = np.array([[amp1, amp2, amp3, amp4]]).reshape(num_points * 4, 1)
  4.     return data, amplitude

(5) 定义一个函数，用于画出将数据传入训练的神经网络后的输出：

  1. # 使用网络画出输出结果
  2. def draw_output(net, num_points_test):
  3.     data_test, amplitude_test = create_waveform(num_points_test)
  4.     output_test = net.sim(data_test)
  5.     plt.plot(amplitude_test.reshape(num_points_test * 4))
  6.     plt.plot(output_test.reshape(num_points_test * 4))

(6) 定义main函数，并生成示例数据：

  1. if __name__=='__main__' :
  2.     # 获取数据
  3.     num_points = 30
  4.     data, amplitude = create_waveform(num_points)

(7) 创建一个两层的递归神经网络：

  1.     # 创建一个两层的神经网络
  2.     net = nl.net.newelm([[-2, 2]], [10, 1], [nl.trans.TanSig(), nl.trans.PureLin()])

(8) 设定每层的初始化函数：

  1.     # 设定初始化函数并进行初始化
  2.     net.layers[0].initf = nl.init.InitRand([-0.1, 0.1], 'wb')
  3.     net.layers[1].initf= nl.init.InitRand([-0.1, 0.1], 'wb')
  4.     net.init()

(9) 训练递归神经网络：

  1.    # 训练递归神经网络
  2.     error = net.train(data, amplitude, epochs=1000, show=100, goal=0.01)

(10) 为训练数据计算来自网络的输出：

  1.    # 计算来自网络的输出
  2.     output = net.sim(data)

(11) 画出训练误差：

  1.     # 画出训练结果
  2.     plt.subplot(211)
  3.     plt.plot(error)
  4.     plt.xlabel('Number of epochs')
  5.     plt.ylabel('Error (MSE)')

(12) 画出结果：

  1.     plt.subplot(212)
  2.     plt.plot(amplitude.reshape(num_points * 4))
  3.     plt.plot(output.reshape(num_points * 4))
  4.     plt.legend(['Ground truth', 'Predicted output'])

(13) 创建一个随机长度的波形，查看该神经网络能否预测：

  1.     # 在多个尺度上对未知数据进行测试
  2.     plt.figure()
  4.     plt.subplot(211)
  5.     draw_output(net, 74)
  6.     plt.xlim([0, 300])

(14) 创建另一个长度更短的波形，查看该神经网络能否预测：

  1.     plt.subplot(212)
  2.     draw_output(net, 54)
  3.     plt.xlim([0, 300])
  5.     plt.show()

(15) 全部代码已经在recurrent_network.py文件中给出。运行该代码，可以看到两幅图像。第一幅图像展示的是训练数据的训练误差及其性能表现，如图11-12所示。

{%}

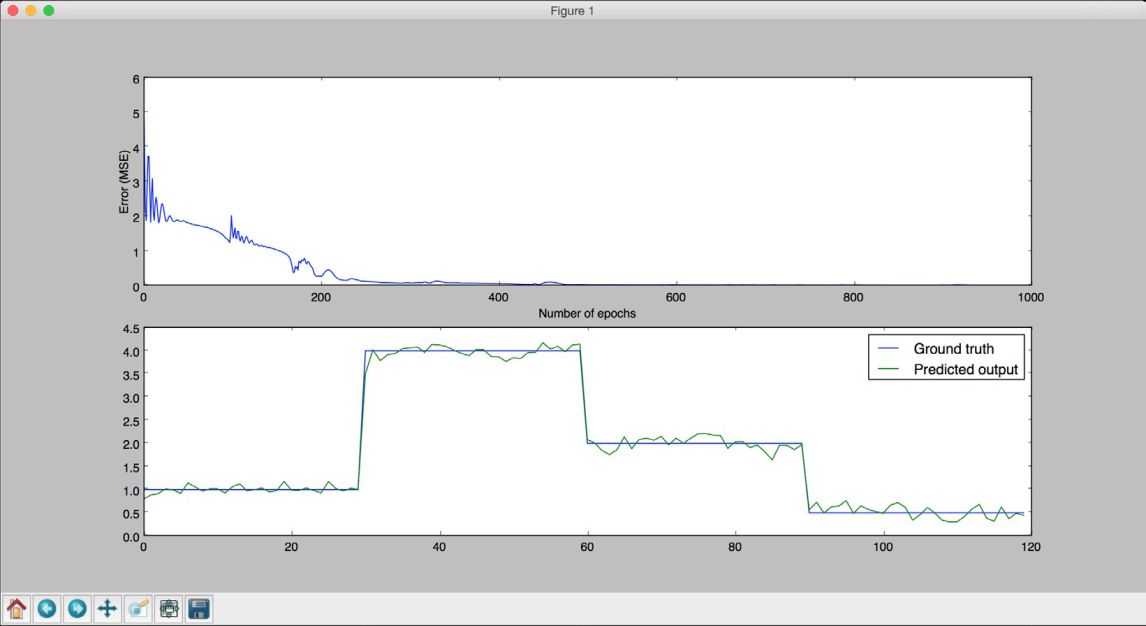
图　11-12

第二幅图像展示的是该训练过的神经网络对于任意长度序列的表现，如图11-13所示。

{%}

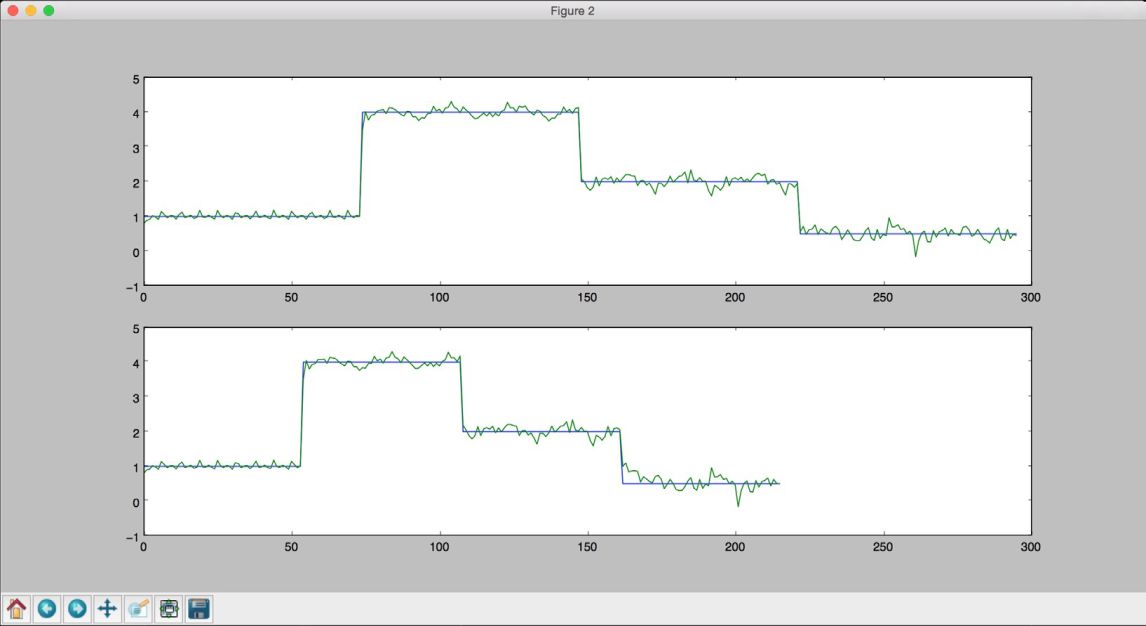
图　11-13

可以在命令行工具中看到如图11-14所示的结果。

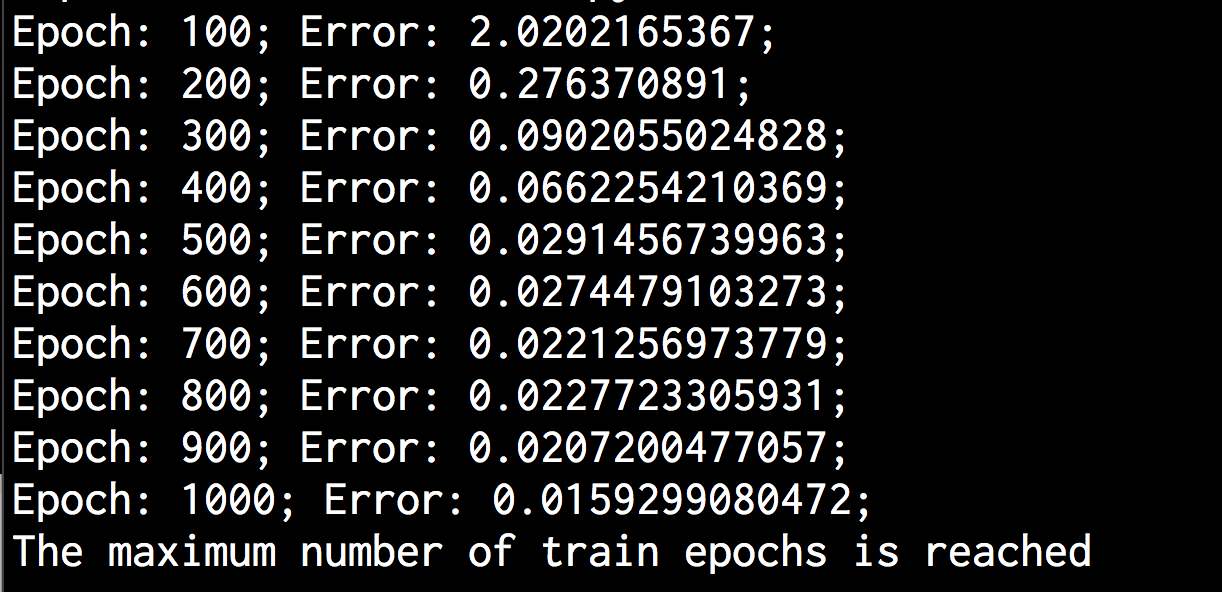
第 11 章　深度神经网络 - 图14

图　11-14

11.7　在光学字符识别数据库中将字符可视化

接下来看看如何利用神经网络做光学字符的识别。光学字符识别是指识别图像中的手写字符的过程。我们会用到http://ai.stanford.edu/~btaskar/ocr中提供的数据集，下载后的默认文件名为letter.data。首先来看如何处理这些数据并将其可视化。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import os
  2. import sys
  4. import cv2
  5. import numpy as np

(2) 定义输入文件名：

  1. # 加载数据
  2. input_file = 'letter.data'

(3) 定义可视化参数：

  1. # 定义可视化参数
  2. scaling_factor = 10
  3. start_index = 6
  4. end_index = -1
  5. h, w = 16, 8

(4) 循环迭代文件直至用户按下Esc键。用Tab分隔符将行分隔成字符：

  1. # 循环直至用户按下Esc键
  2. with open(input_file, 'r') as f:
  3.     for line in f.readlines():
  4.         data = np.array([255*float(x) for x in line.split('\t')
  5.                [start_index:end_index]])

(5) 将数组重新调整为所需的形状，调整大小并将其展示：

  1.         img = np.reshape(data, (h,w))
  2.         img_scaled = cv2.resize(img, None, fx=scaling_factor, fy=scaling_factor)
  3.         cv2.imshow('Image', img_scaled)

(6) 如果用户按下Esc键，则终止循环：

  1.         c = cv2.waitKey()
  2.         if c == 27:
  3.             break

(7) 全部代码已经在visualize_characters.py文件中给出。运行该代码，可以看到一个展示字符的窗体。例如，字母“o”的形状如图11-15所示。

{%}

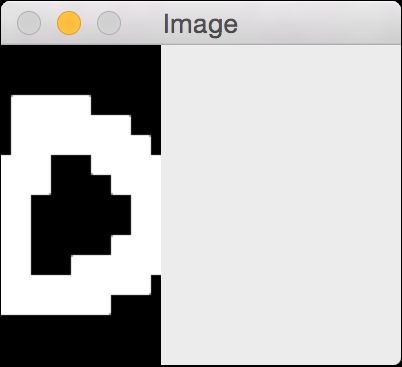
图　11-15

字母“i”的形状如图11-16所示。

{%}

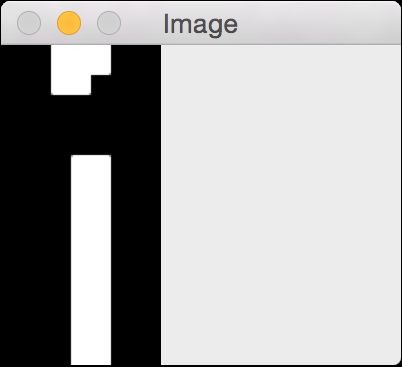
图　11-16

11.8　用神经网络创建一个光学字符识别器

知道如何与数据交互后，接下来创建一个基于神经网络的光学字符识别系统。

详细步骤

(1) 创建一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import neurolab as nl

(2) 定义输入文件名称：

  1. # 输入文件
  2. input_file = 'letter.data'

(3) 在用神经网络处理大量数据时，往往需要花费很多时间来做训练。为了展示如何创建这个系统，这里只使用20个数据点：

  1. # 从输入文件加载数据点
  2. num_datapoints = 20

(4) 观察数据，可以看到在前20行有7个不同的字符。将其定义如下：

  1. # 不同的字符
  2. orig_labels = 'omandig'
  4. # 不同字符的数量
  5. num_output = len(orig_labels)

(5) 用数据集的90%做训练，剩下的10%做测试。定义训练和测试参数如下：

  1. # 定义训练和测试参数
  2. num_train = int(0.9 * num_datapoints)
  3. num_test = num_datapoints - num_train

(6) 数据文件中每行的起始索引值和终止索引值设置如下：

  1. # 定义数据集提取参数
  2. start_index = 6
  3. end_index = -1

(7) 生成数据集：

  1. # 生成数据集
  2. data = []
  3. labels = []
  4. with open(input_file, 'r') as f:
  5.     for line in f.readlines():
  6.         # 按Tab键分割
  7.         list_vals = line.split('\t')

(8) 增加一个错误检查步骤，以查看这些字符是否在标签列表中：

  1.         # 如果字符不在标签列表中，跳过
  2.         if list_vals[1] not in orig_labels:
  3.             continue

(9) 提取标签，并将其添加到主列表的后面：

  1.         # 提取标签，并将其添加到主列表的后面
  2.         label = np.zeros((num_output, 1))
  3.         label[orig_labels.index(list_vals[1])] = 1
  4.         labels.append(label)

(10) 提取字符，并将其添加到主列表的后面：

  1.         # 提取字符，并将其添加到主列表的后面
  2.         cur_char = np.array([float(x) for x in list_vals[start_index:end_index]])
  3.         data.append(cur_char)

(11) 当有足够多数据时跳出循环：

  1.         # 当有足够多数据时跳出循环
  2.         if len(data) >= num_datapoints:
  3.             break

(12) 将以上数据转换成NumPy数组：

  1. # 将数据转换成NumPy数组
  2. data = np.asfarray(data)
  3. labels = np.array(labels).reshape(num_datapoints, num_output)

(13) 提取数据的维度信息：

  1. # 提取数据的维度信息
  2. num_dims = len(data[0])

(14) 用10 000次迭代来训练神经网络：

  1. # 创建并训练神经网络
  2. net = nl.net.newff([[0, 1] for  in range(len(data[0]))], [128, 16, numoutput])
  3. net.trainf = nl.train.train_gd
  4. error = net.train(data[:num_train,:], labels[:num_train,:], epochs=10000,
  5. show=100, goal=0.01)

(15) 为测试输入数据预测输出结构：

  1. # 为测试输入数据预测输出结构
  2. predicted_output = net.sim(data[num_train:, :])
  3. print "\nTesting on unknown data:"
  4. for i in range(num_test):
  5.     print "\nOriginal:", orig_labels[np.argmax(labels[i])]
  6.     print "Predicted:", orig_labels[np.argmax(predicted_output[i])]

(16) 全部代码已经在ocr.py文件中给出。运行该代码，可以在命令行工具中看到如图11-17所示的结果。

第 11 章　深度神经网络 - 图17

图　11-17

神经网络的输出结果如图11-18所示。

第 11 章　深度神经网络 - 图18

图　11-18