第 3 章　预测建模

第 3 章　预测建模

在这一章，我们将介绍以下主题：

用SVM（Support Vector Machines，支持向量机）建立线性分类器
用SVM建立非线性分类器
解决类型数量不平衡问题
提取置信度
寻找最优超参数
建立事件预测器
估算交通流量

3.1　简介

预测建模（Predictive modeling）可能是数据分析中最吸引人的领域之一。近几年，由于大数据在各个垂直领域的蓬勃发展，预测建模备受关注。在数据挖掘领域，预测建模常用来预测未来趋势。

预测建模是一种用来预测系统未来行为的分析技术，它由一群能够识别独立输入变量与反馈目标关联关系的算法构成。我们根据观测值创建一个数学模型，然后用这个模型去预测未来发生的事情。

在预测建模中，需要收集已知的响应数据来训练模型。一旦模型建成，就可以用一些指标来检验它，然后用它预测未来值。可以通过许多种不同的算法来创建预测模型。本章将利用SVM来建立线性模型与非线性模型。

预测模型是用若干可能对系统行为产生影响的特征构建的。例如，如果要预测天气情况，就需要用气温、大气压、降雨量和其他的气象数据。类似地，当处理其他系统问题时，也需要先判断哪些因素可能会影响系统的行为，然后在训练模型之前把这些因素加入特征中。

3.2　用SVM建立线性分类器

SVM是用来构建分类器和回归器的监督学习模型。SVM通过对数学方程组求解，可以找出两组数据之间的最佳分割边界。如果你对SVM不太了解，可以从下面几个不错的教程开始学习：

下面看看如何用SVM建立线性分类器。

3.2.1　准备工作

为了便于理解问题，先对数据进行可视化。我们将参考svm.py文件里已有的源代码。在建立SVM之前，先对数据进行直观的认识。我们将使用源代码文件夹里的data_multivar.txt文件。下面看看如何对数据进行可视化。首先创建一个Python文件，然后在文件中增加下面的代码：

import numpy as np
import matplotlib.pyplot as plt
import utilities
# 加载输入数据
input_file = 'data_multivar.txt'
X, y = utilities.load_data(input_file)

刚刚导入了需要的程序包，然后确定了输入文件的名称。接下来看看load_data()方法：

# 加载输入文件中的多变量数据
def load_data(input_file):
    X = []
    y = []
    with open(input_file, 'r') as f:
        for line in f.readlines():
            data = [float(x) for x in line.split(',')]
            X.append(data[:-1])
            y.append(data[-1])
    X = np.array(X)
    y = np.array(y)
    return X, y

需要将数据分成类，如下所示：

class_0 = np.array([X[i] for i in range(len(X)) if y[i]==0])
class_1 = np.array([X[i] for i in range(len(X)) if y[i]==1])

数据分成类之后，我们把它们画出来：

plt.figure()
plt.scatter(class_0[:,0], class_0[:,1], facecolors='black', edgecolors='black', marker='s')
plt.scatter(class_1[:,0], class_1[:,1], facecolors='None', edgecolors='black', marker='s')
plt.title('Input data')
plt.show()

运行代码，可以看到如图3-1所示的图形。

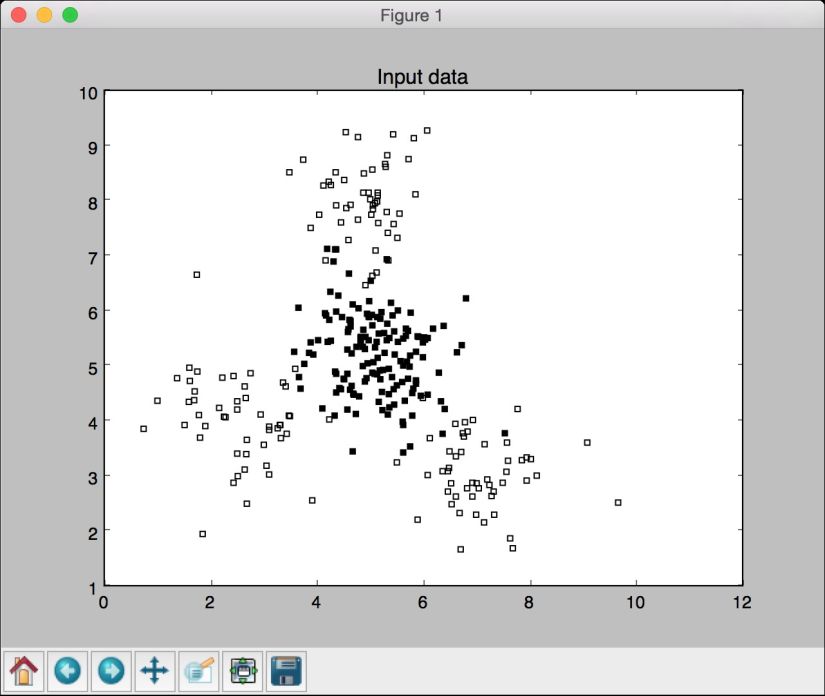
第 3 章　预测建模 - 图1

图　3-1

图3-1由两种类型的数据点构成——实心方块和空心方块。用机器学习的术语说就是，我们的数据由两个类型组成。我们的目标就是要建立一个可以将实心方块和空心方块分开的模型。

3.2.2　详细步骤

(1) 我们需要将数据集分割成训练数据集和测试数据集。在同样的Python文件中加入以下代码：

# 分割数据集并用SVM训练模型
from sklearn import cross_validation
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.25, random_state=5)

(2) 用线性核函数（linear kernel）初始化一个SVM对象。如果你不了解核函数的概念，请参考http://www.eric-kim.net/eric-kim-net/posts/1/kernel_trick.html。在文件中加入以下代码：

params = {'kernel': 'linear'}
classifier = SVC(**params)

(3) 现在可以训练线性SVM分类器了：

classifier.fit(X_train, y_train)

(4) 现在可以看到分类器是如何执行的：

utilities.plot_classifier(classifier, X_train, y_train, 'Training dataset')
plt.show()

(5) 运行代码，可以看到如图3-2所示的图形。

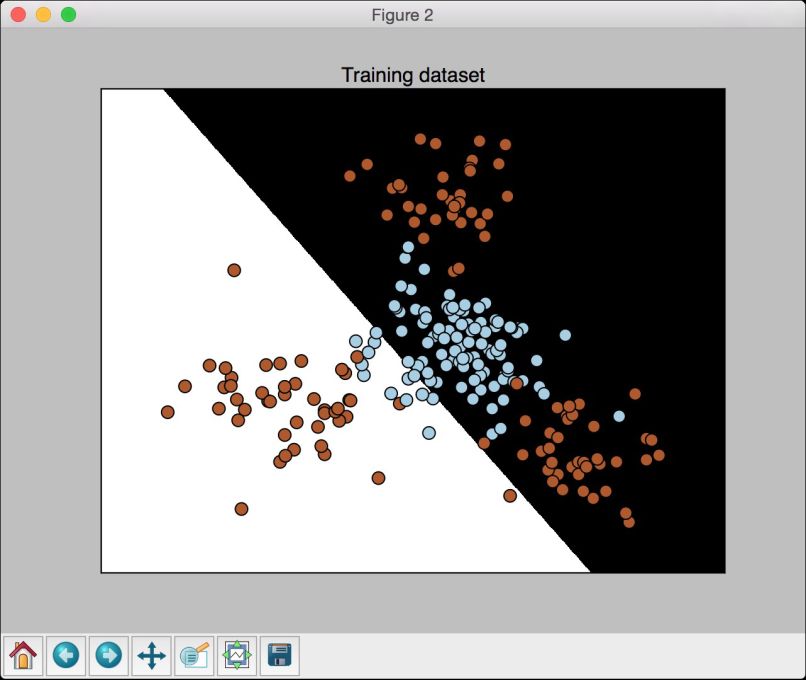
第 3 章　预测建模 - 图2

图　3-2

plot_classifier函数和之前介绍的画图函数一样，只是额外增加了两点内容。你可以在utilities.py文件里查看所有细节。

(6) 接下来看看分类器对测试数据集的执行。在Python文件中增加下面的代码：

y_test_pred = classifier.predict(X_test)
utilities.plot_classifier(classifier, X_test, y_test, 'Test dataset')
plt.show()

(7) 运行代码，可以看到如图3-3所示的图形。

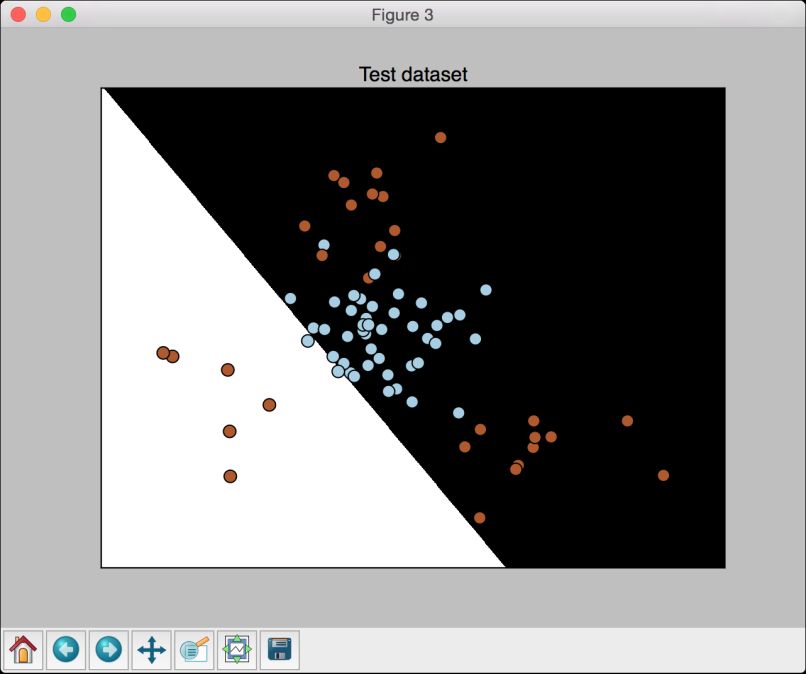
第 3 章　预测建模 - 图3

图　3-3

(8) 接下来计算训练数据集的准确性。在Python文件中增加下面的代码：

from sklearn.metrics import classification_report
target_names = ['Class-' + str(int(i)) for i in set(y)]
print "\n" + "#"30
print "
Classifier performance on training dataset
"
print classification_report(y_train, classifier.predict(X_train), target_names=target_names)
print "#"30 + "\n"

(9) 运行代码，可以在命令行工具中看到如图3-4所示的结果。

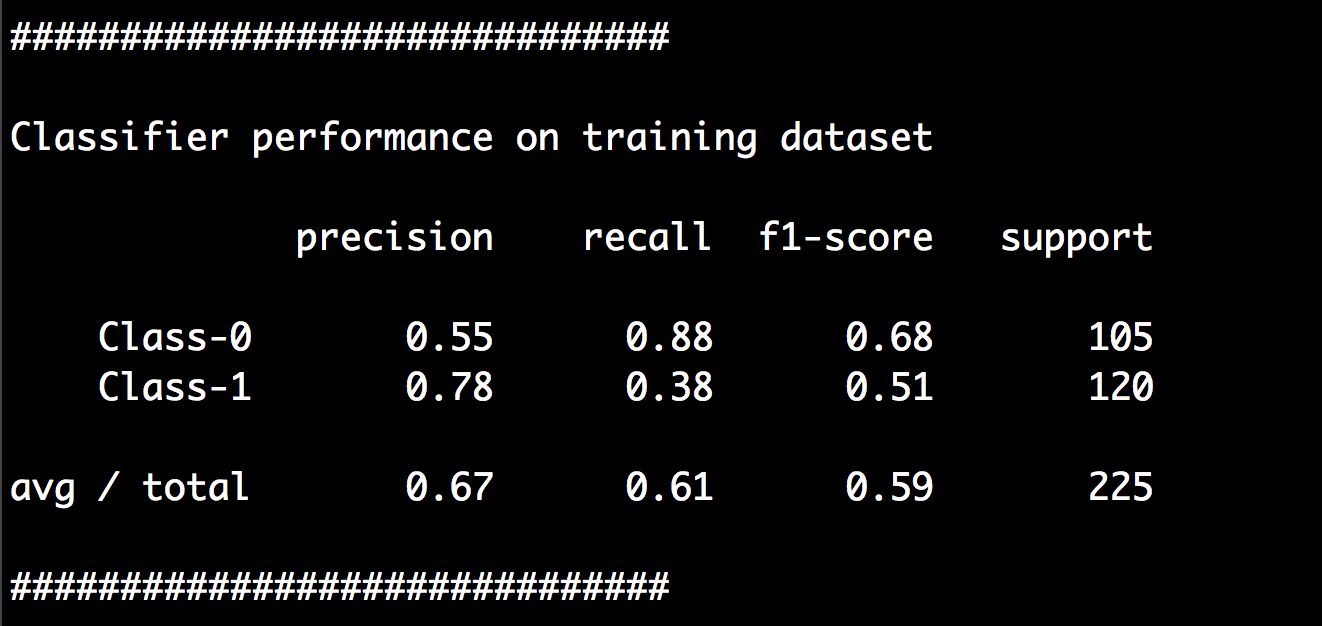
第 3 章　预测建模 - 图4

图　3-4

(10) 最后看看分类器为测试数据集生成的分类报告：

print "#"30
print "
Classification report on test dataset
"
print classification_report(y_test, y_test_pred, target_names=target_names)
print "#"30 + "\n"

(11) 运行代码，可以在命令行工具中看到如图3-5所示的结果。

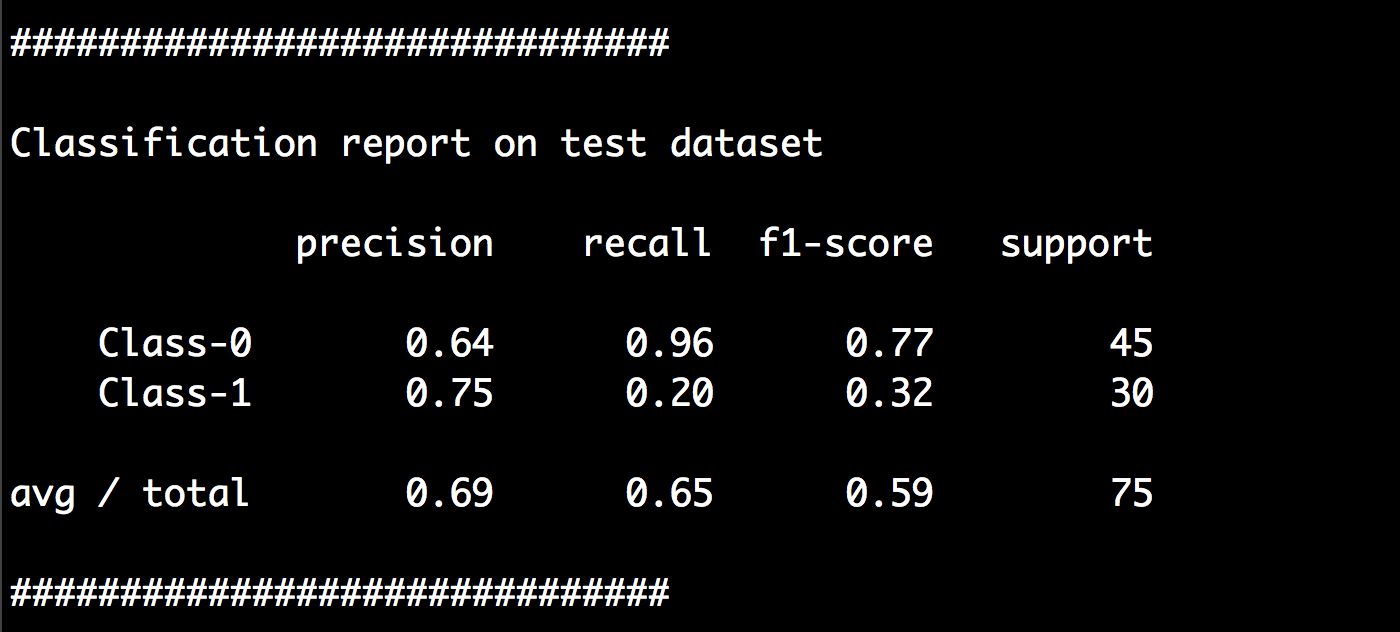
第 3 章　预测建模 - 图5

图　3-5

从前面数据的可视化图中可以看出，实心方块完全是被空心方块包围着的，也就是说两种类型的数据不是线性可分的。我们无法画出一条可以分离两种类型数据点的完美直线，因此需要尝试使用非线性分类器来分离这两种数据。

3.3　用SVM建立非线性分类器

SVM为建立非线性分类器提供了许多选项，需要用不同的核函数建立非线性分类器。为了简单起见，考虑两种情况，当想要表示两种类型数据的曲线边界时，既可以用多项式函数，也可以用径向基函数（Radial Basis Function，RBF）。

详细步骤

(1) 对于第一种情况，可以用一个多项式核函数建立非线性分类器。在同样的Python文件中搜索下面的代码：

params = {'kernel': 'linear'}

将其替换成下面的代码：

params = {'kernel': 'poly', 'degree': 3}

这就表示我们用了一个三次多项式方程。如果增加方程的次数，就表示可以让曲线更加弯曲。但是，曲线越弯曲，意味着训练要花费的时间越长，因为计算强度更大。

(2) 运行代码，可以看到如图3-6所示的图形。

第 3 章　预测建模 - 图6

图　3-6

(3) 还可以在命令行工具中看到如图3-7所示的分类报告。

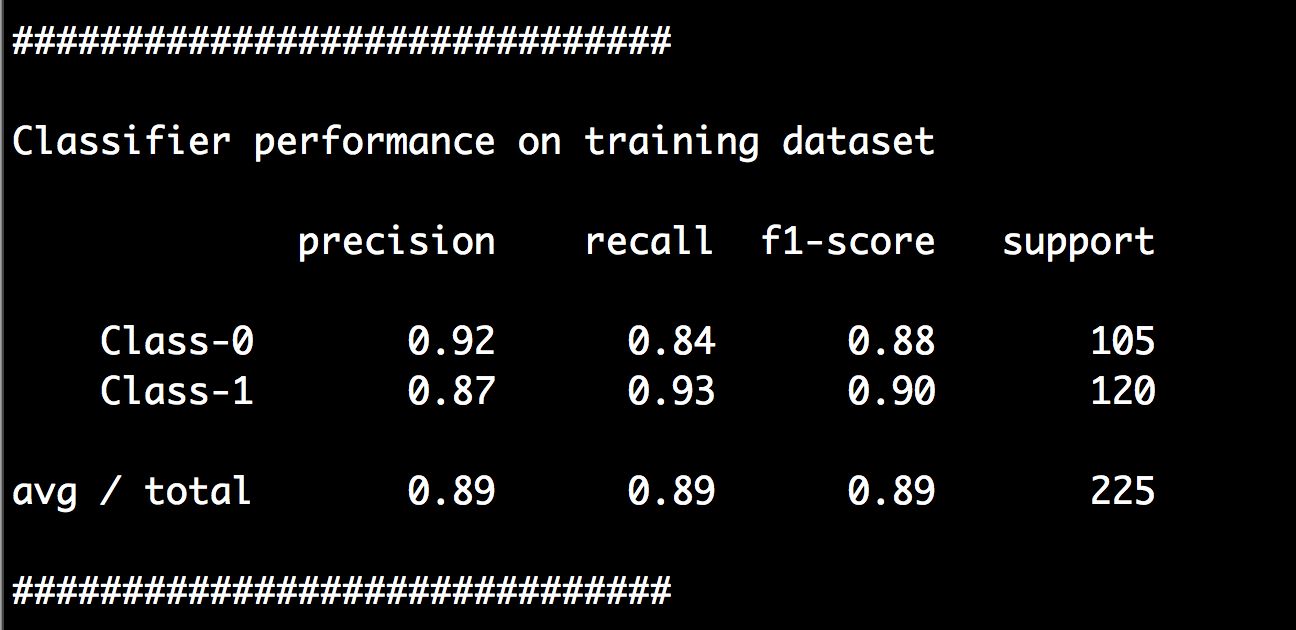
第 3 章　预测建模 - 图7

图　3-7

(4) 我们还可以用径向基函数建立非线性分类器。在同样的Python文件中搜索下面的代码：

params = {'kernel': 'poly', 'degree': 3}

将其替换成：

params = {'kernel': 'rbf'}

(5) 运行代码，可以看到如图3-8所示的图形。

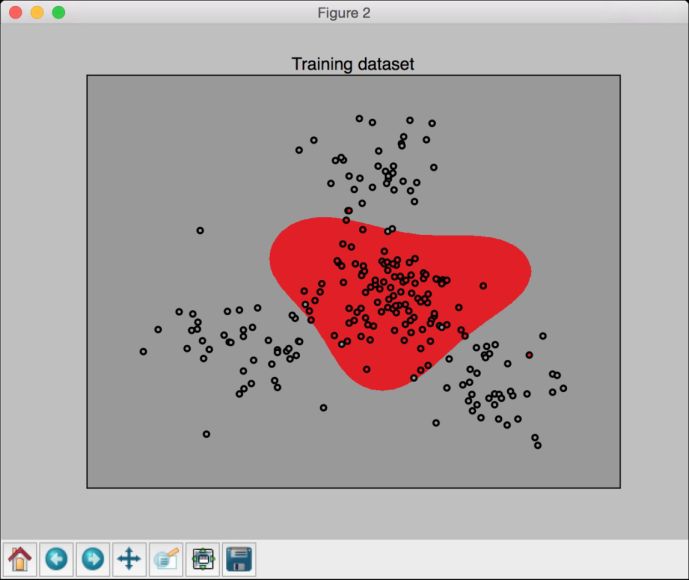
第 3 章　预测建模 - 图8

图　3-8

(6) 还可以在命令行工具中看到如图3-9所示的分类报告。

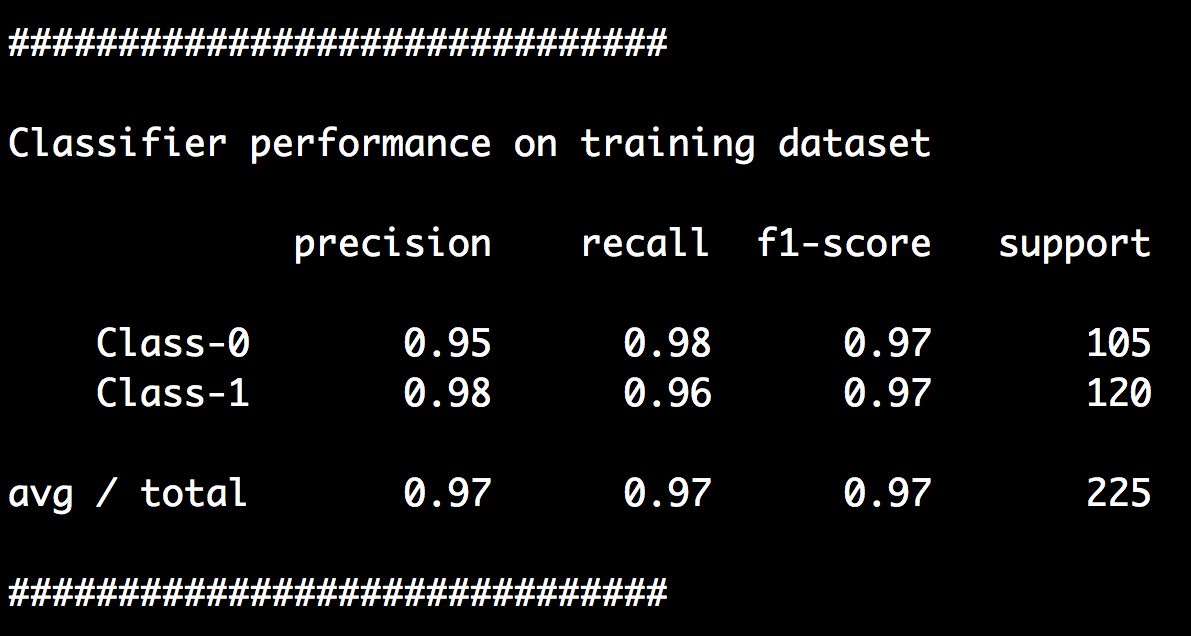
第 3 章　预测建模 - 图9

图　3-9

3.4　解决类型数量不平衡问题

到目前为止，我们处理的问题都是所有类型的数据点数量比较接近的情况，但是在真实世界中，我们不可能总能获取到这么均衡的数据集。有时，某一个类型的数据点数量可能比其他类型多很多，在这种条件下训练的分类器就会有偏差。边界线不会反映数据的真实特性，因为两种类型的数据点数量差别太大。因此，需要慎重考虑这种差异性，并想办法调和，才能保证分类器是不偏不倚的。

详细步骤

(1) 先加载数据：

input_file = 'data_multivar_imbalance.txt'
X, y = utilities.load_data(input_file)

(2) 接下来可视化这些数据。数据可视化的代码和前面章节中的可视化代码完全相同，可以参考svm_imbalance.py文件中的源代码。运行代码，可以看到如图3-10所示的图形。

{%}

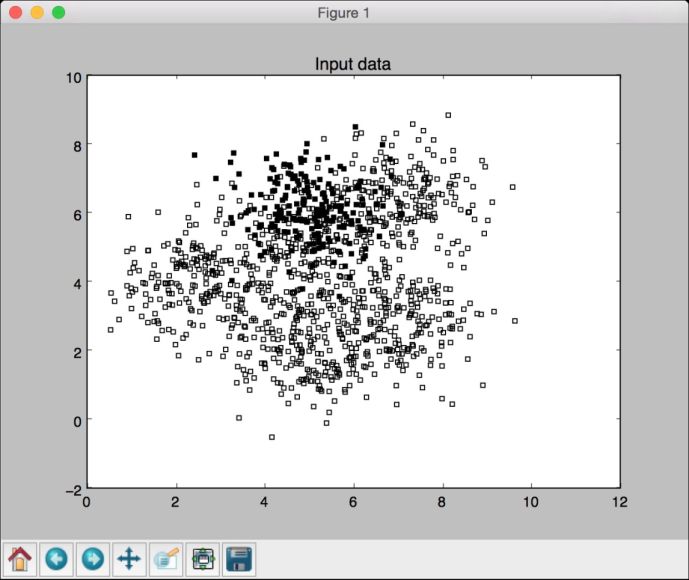
图　3-10

(3) 下面用线性核函数建立一个SVM分类器，代码和前面章节中的代码完全相同。运行代码，可以看到如图3-11所示的图形。

{%}

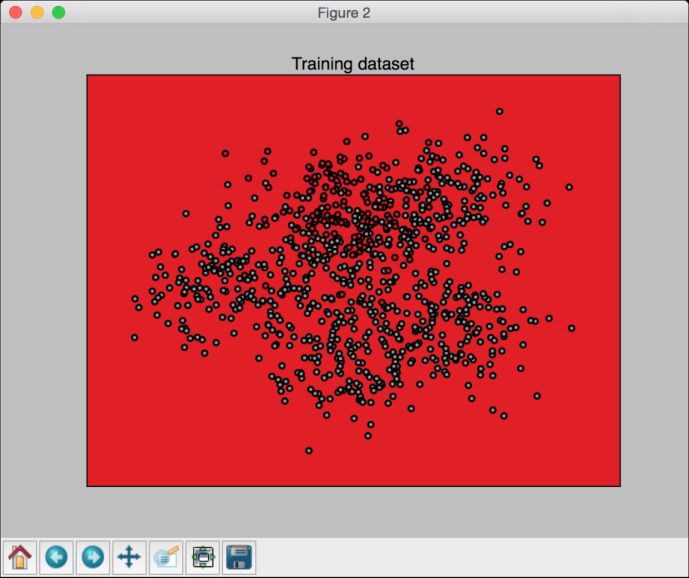
图　3-11

(4) 你可能会奇怪为什么没有边界线了。其实是因为分类器不能区分两种类型，导致Class-0的准确性是0%。可以在命令行工具中看到如图3-12所示的分类报告。

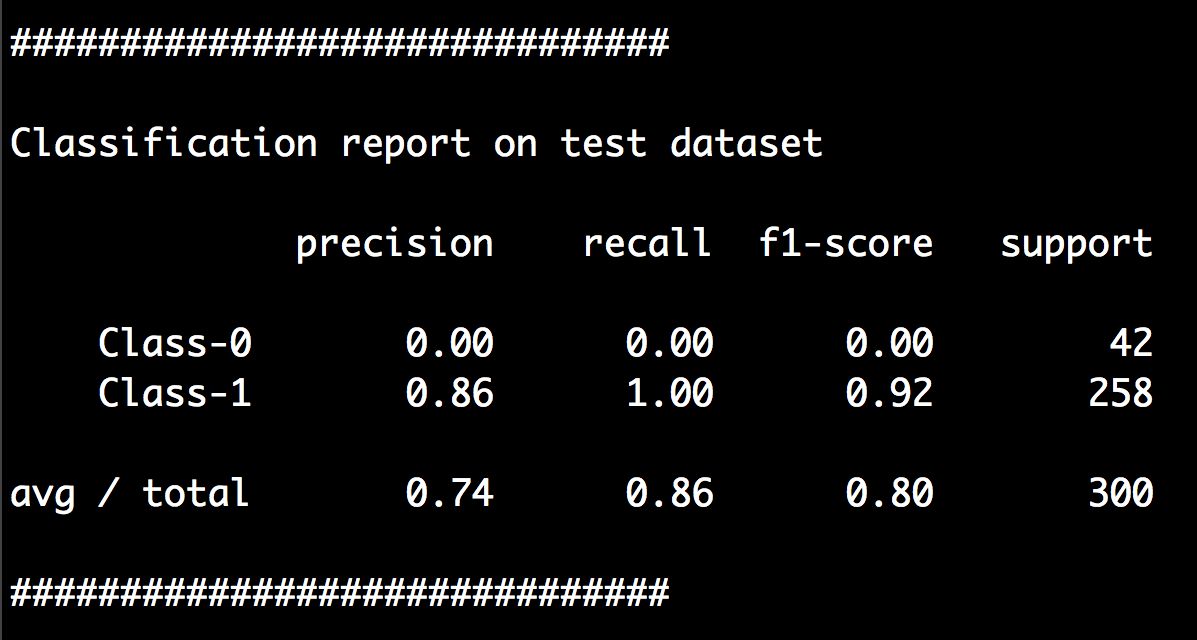
第 3 章　预测建模 - 图12

图　3-12

从图3-12中也可以看出，Class-0的准确性是0%。

(5) 我们继续来解决这个问题。在Python文件中搜索下面的代码：

params = {'kernel': 'linear'}

将其替换成：

params = {'kernel': 'linear', 'class_weight': 'auto'}

参数class_weight的作用是统计不同类型数据点的数量，调整权重，让类型不平衡问题不影响分类效果。

(6) 运行代码，可以看到如图3-13所示的图形。

{%}

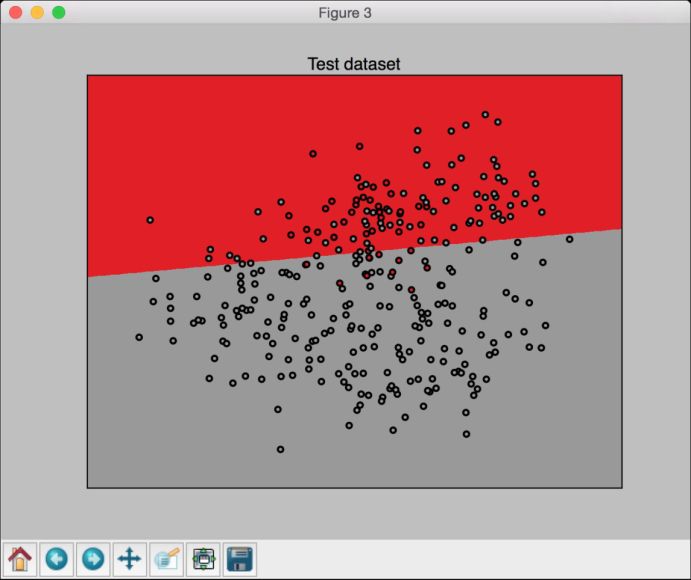
图　3-13

(7) 可以在命令行工具中看到如图3-14所示的分类报告。

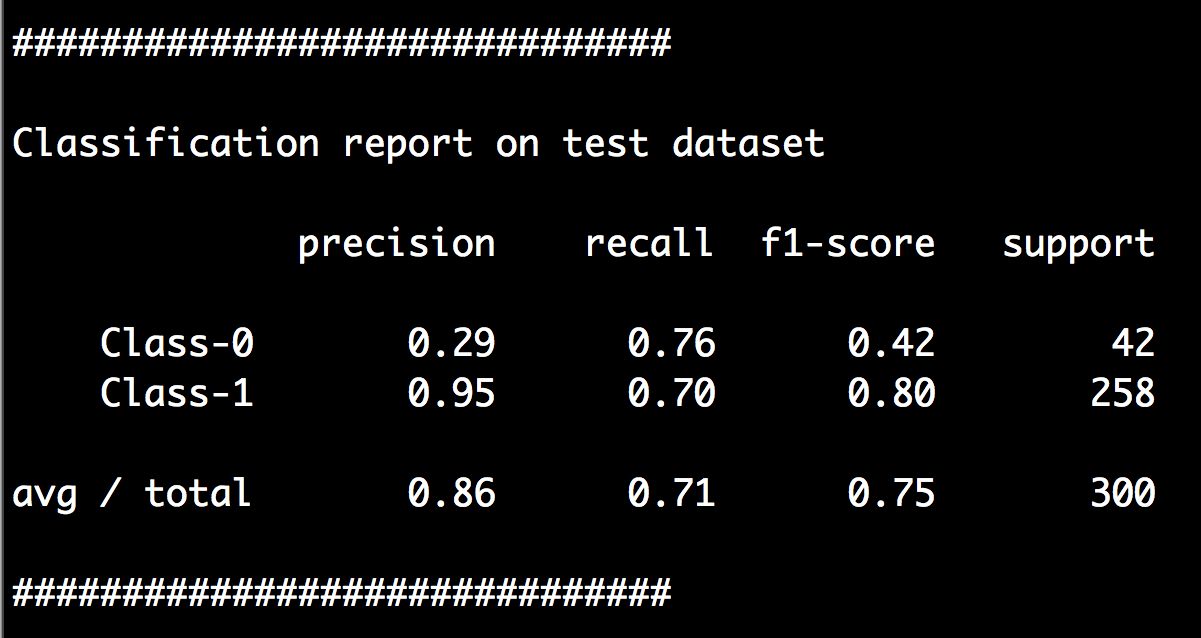
第 3 章　预测建模 - 图14

图　3-14

从图3-14中可以看到，Class-0的准确性不是0%了。

3.5　提取置信度

如果能够获取对未知数据进行分类的置信水平，那将会非常有用。当一个新的数据点被分类为某一个已知类别时，我们可以训练SVM来计算出输出类型的置信度。

详细步骤

(1) 读者可以参考svm_confidence.py文件中的源代码，这里只介绍核心部分。首先，定义以下输入数据：

# 测量数据点与边界的距离
input_datapoints = np.array([[2, 1.5], [8, 9], [4.8, 5.2], [4, 4], [2.5, 7], [7.6, 2], [5.4, 5.9]])

(2) 测量数据点到边界的距离：

print "\nDistance from the boundary:"
for i in input_datapoints:
    print i, '-->', classifier.decision_function(i)[0]

(3) 可以在命令行工具中看到如图3-15所示的结果。

{%}

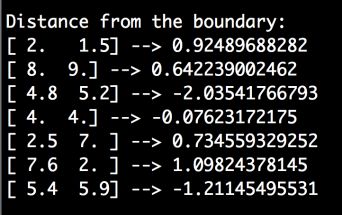
图　3-15

(4) 到边界的距离向我们提供了一些关于数据点的信息，但是它并不能准确地告诉我们分类器能够输出某个类型的置信度有多大。为了解决这个问题，需要用到概率输出（Platt scaling）。概率输出是一种将不同类别的距离度量转换成概率度量的方法。读者可以通过http://fastml.com/classifier-calibration-with-platts-scaling-and-isotonic-regression的教程学习概率输出的内容。下面继续用概率输出来训练SVM：

# 测量置信度
params = {'kernel': 'rbf', 'probability': True}
classifier = SVC(**params)

参数probability用于告诉SVM训练的时候要计算出概率。

(5) 训练分类器：

classifier.fit(X_train, y_train)

(6) 计算输入数据点的置信度：

print "\nConfidence measure:"
for i in input_datapoints:
    print i, '-->', classifier.predict_proba(i)[0]

predict_proba函数用于测量置信值。

(7) 可以在命令行工具中看到如图3-16所示的结果。

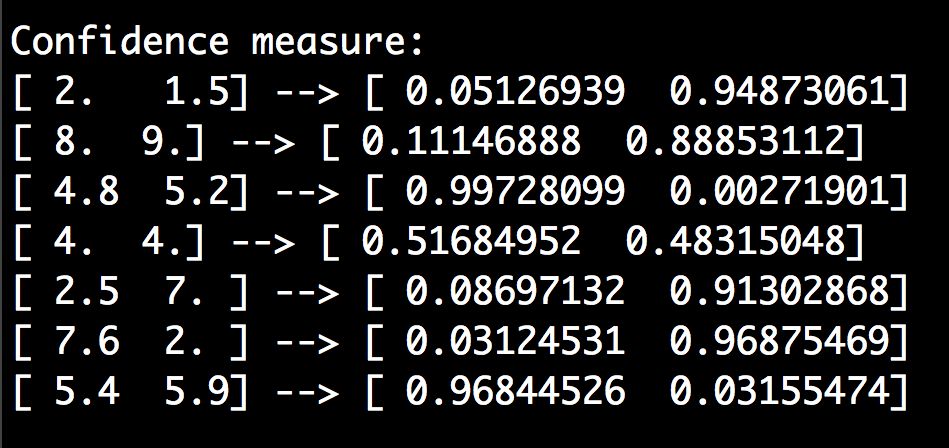
第 3 章　预测建模 - 图16

图　3-16

(8) 再看看数据点与边界的位置：

utilities.plot_classifier(classifier, input_datapoints, [0]*len(input_datapoints), 'Input datapoints', 'True')

(9) 运行代码，可以看到如图3-17所示的图形。

{%}

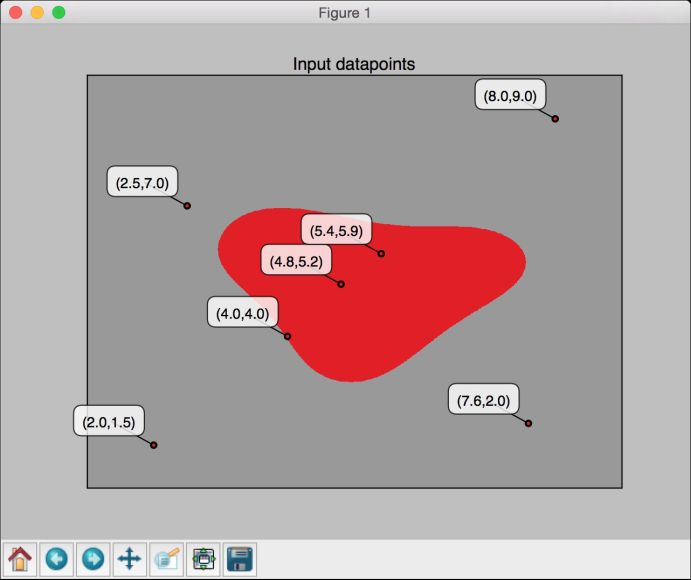
图　3-17

3.6　寻找最优超参数

就像上一章提到的，超参数对分类器的性能至关重要。本节我们看看如何为SVM获取最优的超参数。

详细步骤

(1) 读者可以参考perform_grid_search.py文件中的源代码，这里只介绍核心部分。这里将使用前面介绍过的交叉验证。加载完数据，并将数据分成训练数据集和测试数据集之后，向文件中加入下面的代码：

# 通过交叉检验设置参数
parameter_grid = [  {'kernel': ['linear'], 'C': [1, 10, 50, 600]},
                    {'kernel': ['poly'], 'degree': [2, 3]},
                    {'kernel': ['rbf'], 'gamma': [0.01, 0.001], 'C': [1, 10, 50, 600]},
                 ]

(2) 定义需要使用的指标：

metrics = ['precision', 'recall_weighted']

(3) 下面开始为每个指标搜索最优超参数：

for metric in metrics:
    print "\n#### Searching optimal hyperparameters for", metric
    classifier = grid_search.GridSearchCV(svm.SVC(C=1),
            parameter_grid, cv=5, scoring=metric)
    classifier.fit(X_train, y_train)

(4) 看看指标的得分：

print "\nScores across the parameter grid:"
for params, avg_score,  in classifier.gridscores_:
    print params, '-->', round(avg_score, 3)

(5) 打印出最好的参数集：

print "\nHighest scoring parameter set:", classifier.best_params_

(6) 运行代码，可以在命令行工具中看到如图3-18所示的结果。

{%}

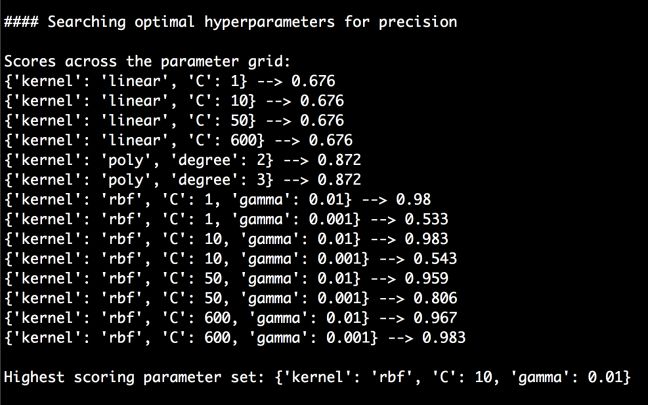
图　3-18

(7) 从图3-18可以发现，模型搜索到了所有的最优超参数。在这个示例中，超参数是内核、C值和gamma的类型。模型将会尝试各种不同参数的组合来搜索最佳参数。接下来在测试数据集上做测试：

y_true, y_pred = y_test, classifier.predict(X_test)
print "\nFull performance report:\n"
print classification_report(y_true, y_pred)

(8) 运行代码，可以在命令行工具中看到如图3-19所示的结果。

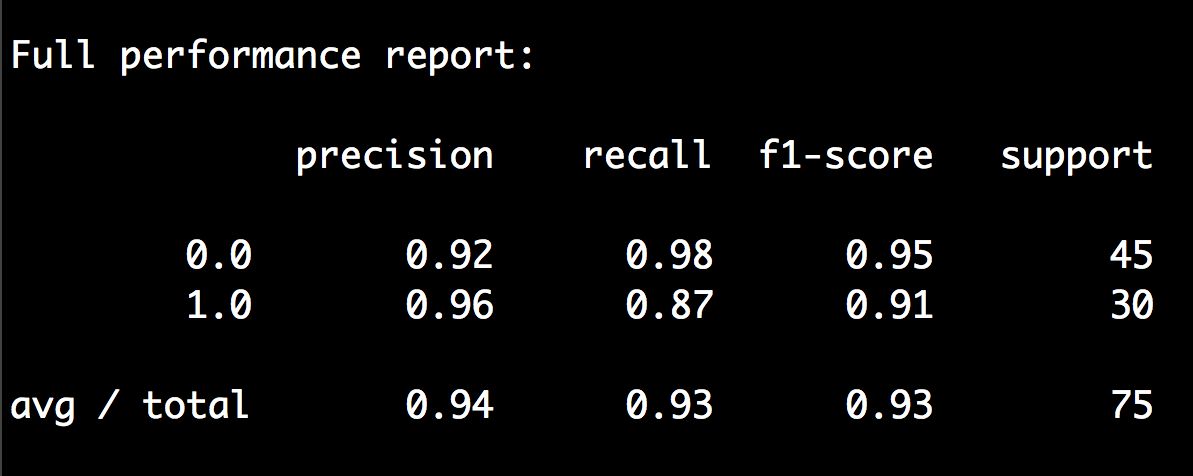
第 3 章　预测建模 - 图19

图　3-19

3.7　建立事件预测器

接下来把所学的知识用于解决真实世界的问题。我们将建立一个SVM来预测一栋大楼进出楼门的人数。该数据集可以在 https://archive.ics.uci.edu/ml/datasets/CalIt2+Building+People+Counts 下载。我们将对数据集稍做调整，以便简化分析过程。调整过的数据集存放在building_event_binary.txt文件和building_event_multiclass.txt文件中。

3.7.1　准备工作

在建立模型之前，我们先看看数据格式。building_event_binary.txt文件的每一行都由6个逗号分割的字符串组成。这6个字符串的排序如下：

星期
日期
时间
离开大楼的人数
进入大楼的人数
是否有活动

前5个字符串组成输入数据，我们的任务是预测大楼是否举行活动。

building_event_multiclass.txt文件的每一行都由6个逗号分割的字符串组成。这个数据集比前面的更细，里面指明了大楼举行活动的类型。这6个字符串的排序如下：

星期
日期
时间
离开大楼的人数
进入大楼的人数
活动类型

前5个字符串是输入数据，我们的任务是预测大楼将举行什么活动。

3.7.2　详细步骤

(1) 读者可以参考event.py文件中的源代码。创建一个Python文件，然后加入下面的代码：

import numpy as np
from sklearn import preprocessing
from sklearn.svm import SVC
input_file = 'building_event_binary.txt'
# 读取数据
X = []
count = 0
with open(input_file, 'r') as f:
    for line in f.readlines():
        data = line[:-1].split(',')
        X.append([data[0]] + data[2:])
X = np.array(X)

我们把数据全部加载到变量X中。

(2) 下面将字符串格式转换成数值格式：

# 将字符串转换成数值
label_encoder = []
X_encoded = np.empty(X.shape)
for i,item in enumerate(X[0]):
    if item.isdigit():
        X_encoded[:, i] = X[:, i]
    else:
        label_encoder.append(preprocessing.LabelEncoder())
        X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])
X = X_encoded[:, :-1].astype(int)
y = X_encoded[:, -1].astype(int)

(3) 用径向基函数、概率输出和类型平衡方法训练SVM分类器：

# 建立SVM模型
params = {'kernel': 'rbf', 'probability': True, 'class_weight': 'auto'}
classifier = SVC(**params)
classifier.fit(X, y)

(4) 现在就可以进行交叉验证了：

# 交叉验证
from sklearn import cross_validation
accuracy = cross_validation.cross_val_score(classifier,
        X, y, scoring='accuracy', cv=3)
print "Accuracy of the classifier: " + str(round(100*accuracy.mean(), 2)) + "%"

(5) 用一个新的数据点测试SVM：

# 对单一数据示例进行编码测试
input_data = ['Tuesday', '12:30:00','21','23']
input_data_encoded = [-1] * len(input_data)
count = 0
for i,item in enumerate(input_data):
    if item.isdigit():
        input_data_encoded[i] = int(input_data[i])
    else:
        input_data_encoded[i] = int(label_encoder[count].transform(input_data[i]))
        count = count + 1
input_data_encoded = np.array(input_data_encoded)
# 为特定数据点预测并打印输出结果
output_class = classifier.predict(input_data_encoded)
print "Output class:", label_encoder[-1].inverse_transform(output_class)[0]

(6) 运行代码，可以在命令行工具中看到如下结果：

Accuracy of the classifier: 89.88%
Output class: event

(7) 如果用building_event_multiclass.txt文件代替building_event_binary.txt文件作为输入数据文件，可以在命令行工具中看到以下结果：

Accuracy of the classifier: 65.9%
Output class: eventA

3.8　估算交通流量

根据相关数据预测交通流量是SVM的一个有趣应用。在上一节中我们将SVM作为一个分类器，下面将它作为一个回归器来估算交通流量。

3.8.1　准备工作

我们将要使用的数据集可以在https://archive.ics.uci.edu/ml/datasets/Dodgers+Loop+Sensor下载。这个数据集统计了洛杉矶道奇棒球队（Los Angeles Dodgers）进行主场比赛期间，体育场周边马路通过的车辆数量，存放在traffic_data.txt文件中。每一行都包含用逗号分隔的字符串格式，如下所示：

星期
时间
对手球队
棒球比赛是否正在继续
通行汽车的数量

3.8.2　详细步骤

(1) 下面看看如何建立SVM回归器。大家可以参考traffic.py文件中的源代码。创建一个Python文件，然后加入下面的代码：

# 用SVM分类器估算交通流量
import numpy as np
from sklearn import preprocessing
from sklearn.svm import SVR
input_file = 'traffic_data.txt'
# 读取数据
X = []
count = 0
with open(input_file, 'r') as f:
    for line in f.readlines():
        data = line[:-1].split(',')
        X.append(data)
X = np.array(X)

我们把数据全部加载到变量X中。

(2) 对数据进行编码：

# 将字符串转换成数值
label_encoder = []
X_encoded = np.empty(X.shape)
for i,item in enumerate(X[0]):
    if item.isdigit():
        X_encoded[:, i] = X[:, i]
    else:
        label_encoder.append(preprocessing.LabelEncoder())
        X_encoded[:, i] = label_encoder[-1].fit_transform(X[:, i])
X = X_encoded[:, :-1].astype(int)
y = X_encoded[:, -1].astype(int)

(3) 用径向基函数创建并训练SVM回归器：

# 建立SVR
params = {'kernel': 'rbf', 'C': 10.0, 'epsilon': 0.2}
regressor = SVR(**params)
regressor.fit(X, y)

在上面的代码中，参数C指定了对错误分类的惩罚，参数epsilon指定了不使用惩罚的限制。

(4) 用交叉验证来检查回归器的性能：

# 交叉验证
import sklearn.metrics as sm
y_pred = regressor.predict(X)
print "Mean absolute error =", round(sm.mean_absolute_error(y, y_pred), 2)

(5) 在一个数据点上进行测试：

# 对单一数据示例进行编码测试
input_data = ['Tuesday', '13:35', 'San Francisco', 'yes']
input_data_encoded = [-1] * len(input_data)
count = 0
for i,item in enumerate(input_data):
    if item.isdigit():
        input_data_encoded[i] = int(input_data[i])
    else:
        input_data_encoded[i] = int(label_encoder[count].transform(input_data[i]))
        count = count + 1
input_data_encoded = np.array(input_data_encoded)
# 为特定数据点预测并打印分类结果
print "Predicted traffic:", int(regressor.predict(input_data_encoded)[0])

(6) 运行代码，可以在命令行工具中看到以下结果：

Mean absolute error = 4.08
Predicted traffic: 29

第 3 章 预测建模

第 3 章 预测建模

3.1 简介

3.2 用SVM建立线性分类器

3.2.1 准备工作

3.2.2 详细步骤

3.3 用SVM建立非线性分类器

详细步骤

3.4 解决类型数量不平衡问题

详细步骤

3.5 提取置信度

详细步骤

3.6 寻找最优超参数

详细步骤

3.7 建立事件预测器

3.7.1 准备工作

3.7.2 详细步骤

3.8 估算交通流量

3.8.1 准备工作

3.8.2 详细步骤

第 3 章　预测建模

第 3 章　预测建模

3.1　简介

3.2　用SVM建立线性分类器

3.2.1　准备工作

3.2.2　详细步骤

3.3　用SVM建立非线性分类器

3.4　解决类型数量不平衡问题

3.5　提取置信度

3.6　寻找最优超参数

3.7　建立事件预测器

3.7.1　准备工作

3.7.2　详细步骤

3.8　估算交通流量

3.8.1　准备工作

3.8.2　详细步骤