第 4 章　无监督学习——聚类

第 4 章　无监督学习——聚类

在这一章，我们将介绍以下主题：

用k-means算法聚类数据
用向量量化（vector quantization）压缩图片
建立均值漂移（Mean Shift）聚类模型
用凝聚层次聚类（agglomerative clustering）进行数据分组
评价聚类算法的聚类效果
用DBSCAN算法自动估算集群数量
探索股票数据的模式
建立客户细分模型

4.1　简介

无监督学习是一种对不含标记的数据建立模型的机器学习范式。到目前为止，我们处理的数据都带有某种形式的标记，也就是说，学习算法可以根据标记看到这些数据，并对数据进行分类。但是，在无监督学习的世界中，我们没有这样的条件了。当需要用一些相似性指标对数据集进行分组时，就会用到这些算法了。

最常见的无监督学习方法就是聚类，你一定对这个词耳熟能详。当需要把无标记的数据分成几种集群时，就要用它来分析。这些集群通常是根据某种相似度指标进行划分的，例如欧氏距离（Euclidean distance）。无监督学习广泛应用于各种领域，如数据挖掘、医学影像、股票市场分析、计算机视觉、市场细分等。

4.2　用k-means算法聚类数据

k-means算法是最流行的聚类算法之一。这个算法常常利用数据的不同属性将输入数据划分为k组。分组是使用最优化的技术实现的，即让各组内的数据点与该组中心点的距离平方和最小化。如果你对k-means算法不太了解，可以在http://www.onmyphd.com/?p=k-means.clustering&ckattempt=1上学习。

详细步骤

(1) 本节的完整代码已经放在kmeans.py文件中。我们先创建一个新的Python文件，然后导入下面的程序包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.cluster import KMeans
import utilities

(2) 加载输入数据，然后定义集群的数量。我们将使用data_multivar.txt 数据文件：

data = utilities.load_data('data_multivar.txt')
num_clusters = 4

(3) 我们需要看看输入数据是什么样子的。继续向Python文件中加入下面的代码：

plt.figure()
plt.scatter(data[:,0], data[:,1], marker='o',
        facecolors='none', edgecolors='k', s=30)
x_min, x_max = min(data[:, 0]) - 1, max(data[:, 0]) + 1
y_min, y_max = min(data[:, 1]) - 1, max(data[:, 1]) + 1
plt.title('Input data')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())

运行代码，可以看到如图4-1所示的图形。

{%}

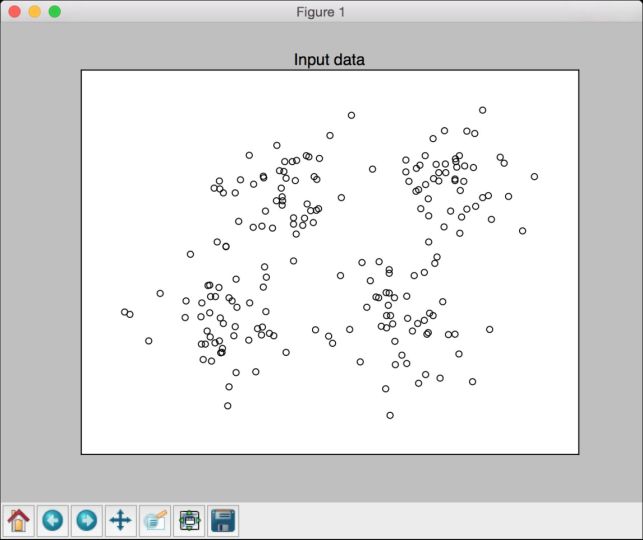
图　4-1

(4) 现在可以训练模型了。先初始化一个k-means对象，然后训练它：

kmeans = KMeans(init='k-means++', n_clusters=num_clusters, n_init=10)
kmeans.fit(data)

(5) 数据训练之后，我们需要可视化边界。继续向Python文件中加入下面的代码：

# 设置网格数据的步长
step_size = 0.01
# 画出边界
x_min, x_max = min(data[:, 0]) - 1, max(data[:, 0]) + 1
y_min, y_max = min(data[:, 1]) - 1, max(data[:, 1]) + 1
x_values, y_values = np.meshgrid(np.arange(x_min, x_max, step_size), np.arange(y_min, y_max, step_size))
# 预测网格中所有数据点的标记
predicted_labels = kmeans.predict(np.c_[x_values.ravel(), y_values.ravel()])

(6) 我们已经通过网格数据评估了模型。接下来把这些结果都画出来，看看边界线的布局：

# 画出结果
predicted_labels = predicted_labels.reshape(x_values.shape)
plt.figure()
plt.clf()
plt.imshow(predicted_labels, interpolation='nearest',
           extent=(x_values.min(), x_values.max(), y_values.min(), y_values.max()),
           cmap=plt.cm.Paired,
           aspect='auto', origin='lower')
plt.scatter(data[:,0], data[:,1], marker='o',
        facecolors='none', edgecolors='k', s=30)

(7) 把中心点画在图形上：

centroids = kmeans.cluster_centers_
plt.scatter(centroids[:,0], centroids[:,1], marker='o', s=200, linewidths=3,
        color='k', zorder=10, facecolors='black')
x_min, x_max = min(data[:, 0]) - 1, max(data[:, 0]) + 1
y_min, y_max = min(data[:, 1]) - 1, max(data[:, 1]) + 1
plt.title('Centoids and boundaries obtained using KMeans')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()

运行代码，可以看到如图4-2所示的图形。

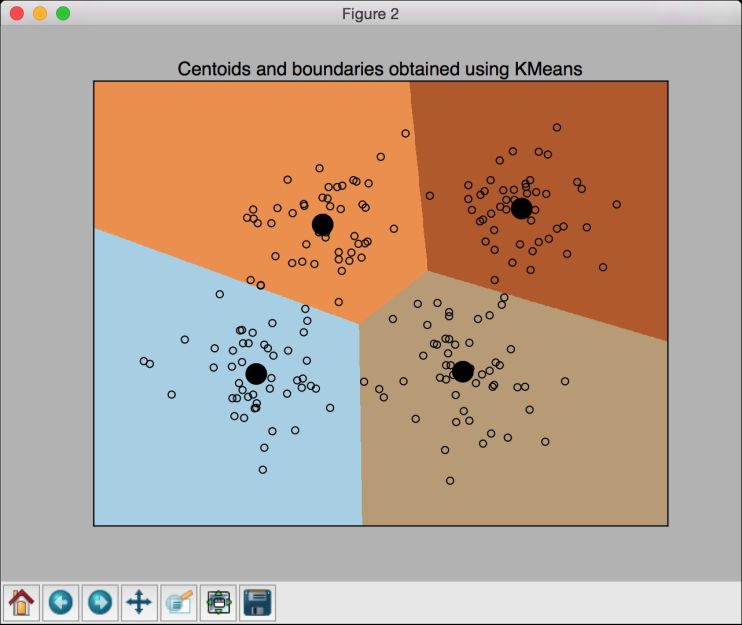
第 4 章　无监督学习——聚类 - 图2

图　4-2

4.3　用矢量量化压缩图片

k-means聚类的主要应用之一就是矢量量化。简单来说，矢量量化就是“四舍五入”（rounding off）的N维版本。在处理数字等一维数据时，会用四舍五入技术减少存储空间。例如，如果只需要精确到两位小数，那么不会直接存储23.73473572，而是用23.73来代替。如果不关心小数部分，甚至可以直接存储24，这取决于我们的真实需求。

同理，当把四舍五入这个概念推广到N维数据时，就变成了矢量量化。当然，矢量量化的细节很多，你可以在http://www.data-compression.com/vq.shtml里学习更多的内容。矢量量化被广泛应用于图片压缩，我们用比原始图像更少的比特数来存储每个像素，从而实现图像图片。

详细步骤

(1) 本例的完整代码已经放在vector_quantization.py文件中。下面看看它是如何实现的。首先需要导入一些程序库。创建一个新的Python文件，然后加入下面的代码：

import argparse
import numpy as np
from scipy import misc
from sklearn import cluster
import matplotlib.pyplot as plt

(2) 创建一个函数，用来解析输入参数。我们需要把图片和每个像素被压缩的比特数传进去作为输入参数：

def build_arg_parser():
    parser = argparse.ArgumentParser(description='Compress the input image \
            using clustering')
    parser.add_argument("--input-file", dest="input_file", required=True,
            help="Input image")
    parser.add_argument("--num-bits", dest="num_bits", required=False,
            type=int, help="Number of bits used to represent each pixel")
    return parser

(3) 再创建一个函数，用来压缩输入的图片：

def compress_image(img, num_clusters):
    # 将输入的图片转换成（样本量，特征量） 数组，以运行k-means聚类算法
    X = img.reshape((-1, 1))
    # 对输入数据运行k-means聚类
    kmeans = cluster.KMeans(n_clusters=num_clusters, n_init=4, random_state=5)
    kmeans.fit(X)
    centroids = kmeans.cluster_centers_.squeeze()
    labels = kmeans.labels_
    # 为每个数据配置离它最近的中心点，并转变为图片的形状
    input_image_compressed = np.choose(labels, centroids).reshape(img.shape)
    return input_image_compressed

(4) 压缩完图片之后，我们需要看看压缩算法对图片质量的影响。下面定义画图函数：

def plot_image(img, title):
    vmin = img.min()
    vmax = img.max()
    plt.figure()
    plt.title(title)
    plt.imshow(img, cmap=plt.cm.gray, vmin=vmin, vmax=vmax)

(5) 我们现在已经准备好所有的函数了。下面定义主函数main，它可以把输入参数传进去并进行处理，然后提取输出图片：

if __name__=='__main__':
    args = build_arg_parser().parse_args()
    input_file = args.input_file
    num_bits = args.num_bits
    if not 1 <= num_bits <= 8:
        raise TypeError('Number of bits should be between 1 and 8')
    num_clusters = np.power(2, num_bits)
    # 打印压缩率
    compression_rate = round(100 * (8.0 - args.num_bits)  8.0, 2)
    print "
The size of the image will be reduced by a factor of", 8.0args.num_bits
    print "\nCompression rate = " + str(compression_rate) + "%"

(6) 加载输入图片：

    # 加载输入图片
    input_image = misc.imread(input_file, True).astype(np.uint8)
    # 显示原始图片
    plot_image(input_image, 'Original image')

(7) 用输入的参数压缩图片：

    # 压缩图片
    input_image_compressed = compress_image(input_image, num_clusters)
    plot_image(input_image_compressed, 'Compressed image; compression rate = '
            + str(compression_rate) + '%')
    plt.show()

(8) 现在我们的代码已经准备好了。在命令行工具中运行下面的命令：

$ python vector_quantization.py --input-file flower_image.jpg --num-bits 4

输入的图片如图4-3所示。

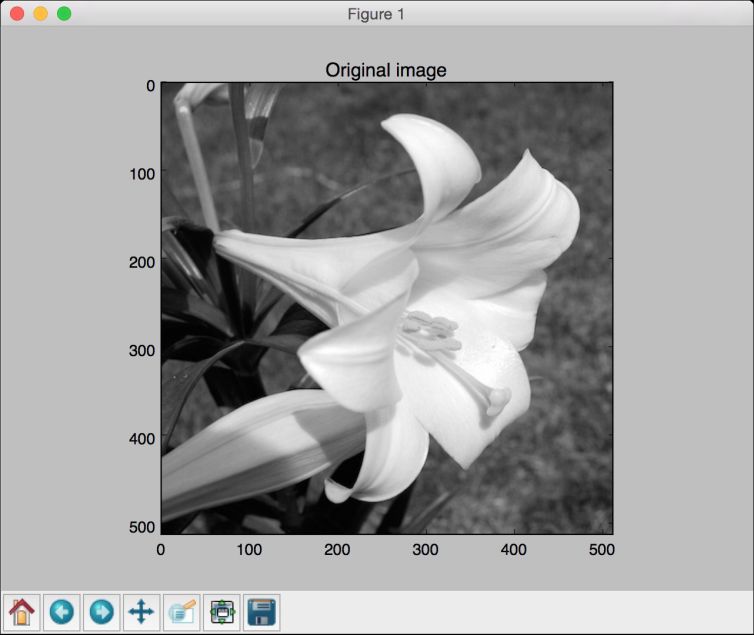
第 4 章　无监督学习——聚类 - 图3

图　4-3

压缩过的图片如图4-4所示。

{%}

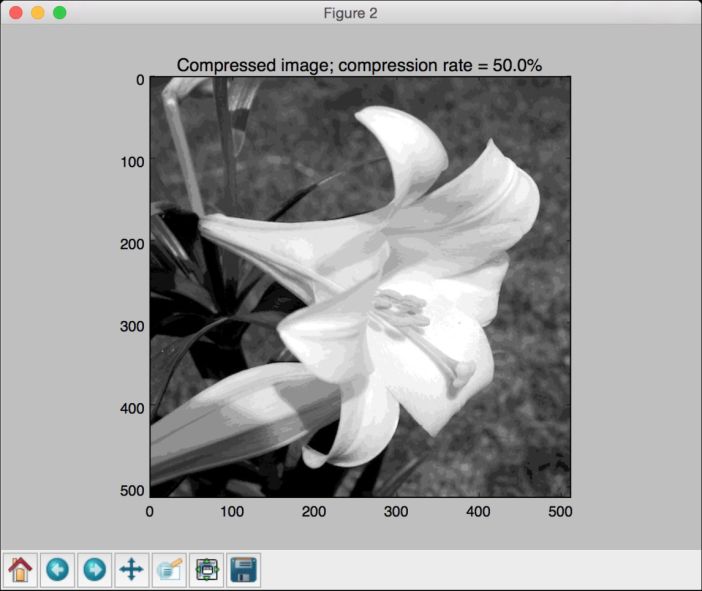
图　4-4

(9) 我们把每个像素的压缩比特数降到2，再压缩图片。在命令行工具中运行下面的命令：

$ python vector_quantization.py --input-file flower_image.jpg --num-bits 2

可以看到压缩过的图片如图4-5所示。

{%}

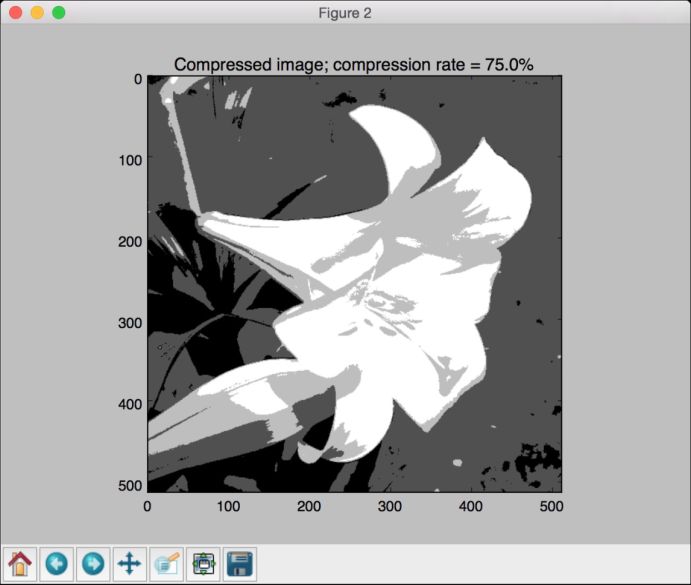
图　4-5

(10) 如果把每个像素的压缩比特数降到1，可以看到只有黑白两种颜色的二进制图像。运行下面的命令：

$ python vector_quantization.py --input-file flower_image.jpg --num-bits 1

图片压缩效果如图4-6所示。

{%}

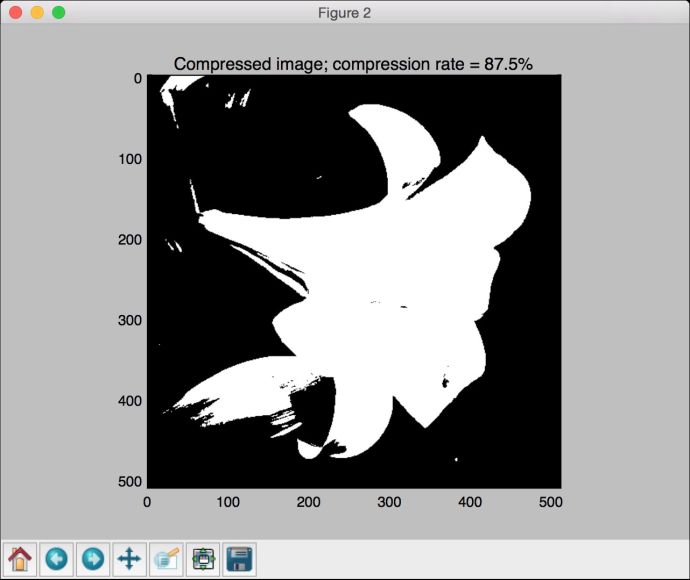
图　4-6

4.4　建立均值漂移聚类模型

均值漂移是一种非常强大的无监督学习算法，用于集群数据点。该算法把数据点的分布看成是概率密度函数（probability-density function），希望在特征空间中根据函数分布特征找出数据点的“模式”（mode）。这些“模式”就对应于一群群局部最密集（local maxima）分布的点。均值漂移算法的优点是它不需要事先确定集群的数量。

假设有一组输入点，我们要在不知道要寻找多少集群的情况下找到它们。均值漂移算法就可以把这些点看成是服从某个概率密度函数的样本。如果这些数据点有集群，那么它们对应于概率密度函数的峰值。该算法从一个随机点开始，逐渐收敛于各个峰值。你可以在 http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/TUZEL1/MeanShift.pdf中学习更详细的内容。

详细步骤

(1) 本例的完整代码已经放在mean_shift.py文件中。我们看看它是如何实现的。首先创建一个新的Python文件，然后导入一些需要用到的程序包：

import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
import utilities

(2) 从data_multivar.txt文件中加载输入数据：

# 从输入文件加载数据
X = utilities.load_data('data_multivar.txt')

(3) 通过指定输入参数创建一个均值漂移模型：

# 设置带宽参数bandwidth
bandwidth = estimate_bandwidth(X, quantile=0.1, n_samples=len(X))
# 用MeanShift计算聚类
meanshift_estimator = MeanShift(bandwidth=bandwidth, bin_seeding=True)

(4) 训练模型：

meanshift_estimator.fit(X)

(5) 提取标记：

labels = meanshift_estimator.labels_

(6) 从模型中提取集群的中心点，然后打印集群数量：

centroids = meanshift_estimator.cluster_centers_
num_clusters = len(np.unique(labels))
print "Number of clusters in input data =", num_clusters

(7) 把集群可视化：

# 画出数据点和聚类中心
import matplotlib.pyplot as plt
from itertools import cycle
plt.figure()
# 为每种集群设置不同的标记
markers = '.*xv'

(8) 迭代数据点并画出它们：

for i, marker in zip(range(num_clusters), markers):
    # 画出属于某个集群中心的数据点
    plt.scatter(X[labels==i, 0], X[labels==i, 1], marker=marker, color='k')
    # 画出集群中心
    centroid = centroids[i]
    plt.plot(centroid[0], centroid[1], marker='o', markerfacecolor='k',
             markeredgecolor='k', markersize=15)
plt.title('Clusters and their centroids')
plt.show()

(9) 运行代码，可以看到如图4-7所示的图形。

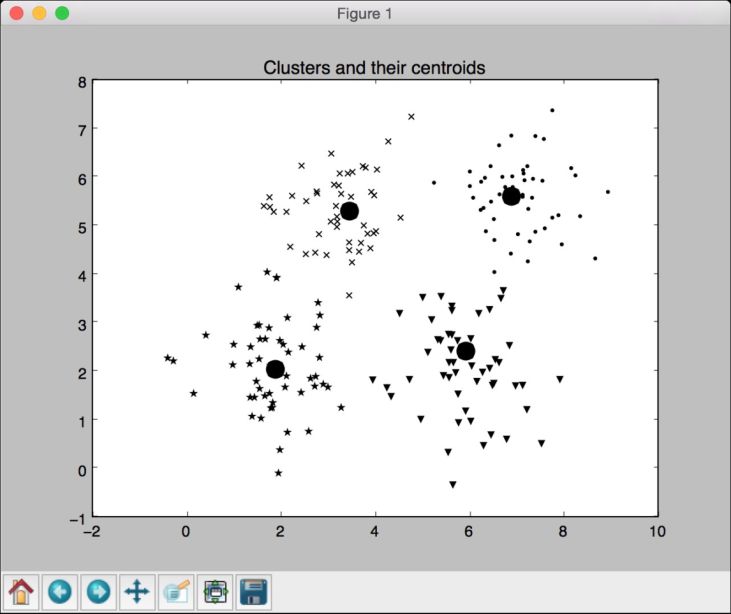
第 4 章　无监督学习——聚类 - 图7

图　4-7

4.5　用凝聚层次聚类进行数据分组

在介绍凝聚层次聚类之前，我们需要先理解层次聚类（hierarchical clustering）。层次聚类是一组聚类算法，通过不断地分解或合并集群来构建树状集群（tree-like clusters）。层次聚类的结构可以用一颗树表示。

层次聚类算法可以是自下而上的，也可以是自上而下的。具体是什么含义呢？在自下而上的算法中，每个数据点都被看作是一个单独的集群。这些集群不断地合并，直到所有的集群都合并成一个巨型集群。这被称为凝聚层次聚类。与之相反的是，自上而下层次的算法是从一个巨大的集群开始，不断地分解，直到所有的集群变成一个单独的数据点。你可以在http://nlp.stanford.edu/IR-book/html/htmledition/hierarchical-agglomerative-clustering-1.html学习更多的内容。

详细步骤

(1) 本例的完整代码都已经放在agglomerative.py文件中。让我们看看它是如何实现的。首先创建一个新的Python文件，然后导入一些需要用到的程序包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import AgglomerativeClustering
from sklearn.neighbors import kneighbors_graph

(2) 定义一个实现凝聚层次聚类的函数：

def perform_clustering(X, connectivity, title, num_clusters=3, linkage='ward'):
    plt.figure()
    model = AgglomerativeClustering(linkage=linkage,
                    connectivity=connectivity, n_clusters=num_clusters)
    model.fit(X)

(3) 提取标记，然后指定不同聚类在图形中的标记：

    # 提取标记
    labels = model.labels_
    # 为每种集群设置不同的标记
    markers = '.vx'

(4) 迭代数据，用不同的标记把聚类的点画在图形中：

    for i, marker in zip(range(num_clusters), markers):
        # 画出属于某个集群中心的数据点
        plt.scatter(X[labels==i, 0], X[labels==i, 1], s=50,
                    marker=marker, color='k', facecolors='none')
    plt.title(title)

(5) 为了演示凝聚层次聚类的优势，我们用它对一些在空间中是连接在一起、但彼此却非常接近的数据进行聚类。我们希望连接在一起的数据可以聚成一类，而不是在空间上非常接近的点聚成一类。下面定义一个函数来获取一组呈螺旋状的数据点：

def get_spiral(t, noise_amplitude=0.5):
    r = t
    x = r  np.cos(t)
    y = r  np.sin(t)
    return add_noise(x, y, noise_amplitude)

(6) 在上面的函数中，我们增加了一些噪声，因为这样做可以增加一些不确定性。下面定义噪声函数：

def add_noise(x, y, amplitude):
    X = np.concatenate((x, y))
    X += amplitude * np.random.randn(2, X.shape[1])
    return X.T

(7) 我们再定义一个函数来获取位于玫瑰曲线上的数据点（rose curve，又称为rhodonea curve，极坐标中的正弦曲线）：

def get_rose(t, noise_amplitude=0.02):
    # 设置玫瑰曲线方程；如果变量k是奇数，那么曲线有k朵花瓣；如果k是偶数，那么有2k朵花瓣
    k = 5
    r = np.cos(k*t) + 0.25
    x = r  np.cos(t)
    y = r  np.sin(t)
    return add_noise(x, y, noise_amplitude)

(8) 为了增加多样性，我们再定义一个hypotrochoid函数：

def get_hypotrochoid(t, noise_amplitude=0):
    a, b, h = 10.0, 2.0, 4.0
    x = (a - b)  np.cos(t) + h  np.cos((a - b) / b  t)
    y = (a - b)  np.sin(t) - h  np.sin((a - b) / b  t)
    return add_noise(x, y, 0)

(9) 现在可以定义主函数main了：

if __name__=='__main__':
    # 生成样本数据
    n_samples = 500
    np.random.seed(2)
    t = 2.5  np.pi  (1 + 2 * np.random.rand(1, n_samples))
    X = get_spiral(t)
    # 不考虑螺旋形的数据连接性
    connectivity = None
    perform_clustering(X, connectivity, 'No connectivity')
    # 根据数据连接线创建K个临近点的图形
    connectivity = kneighbors_graph(X, 10, include_self=False)
    perform_clustering(X, connectivity, 'KNeighbors connectivity')
    plt.show()

(10) 运行代码，可以看到如图4-8所示的图形（没有用任何连接特征）。

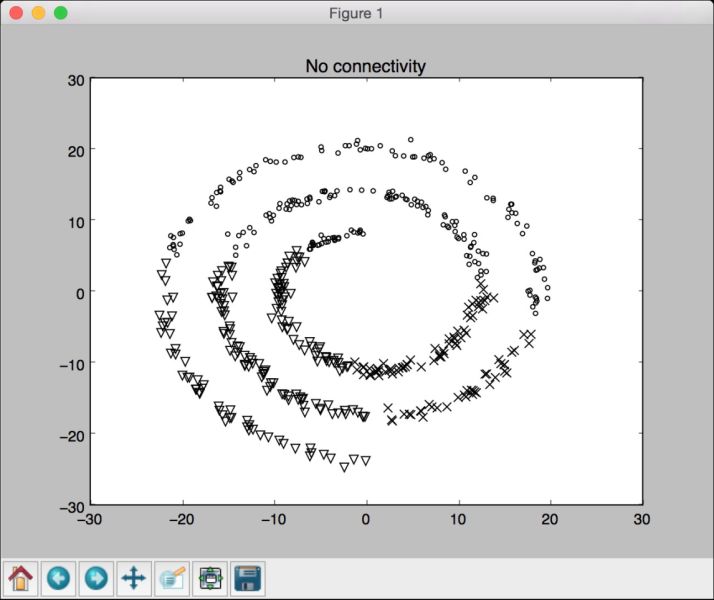
第 4 章　无监督学习——聚类 - 图8

图　4-8

(11) 还可以看到如图4-9所示的图形（使用连接特征）。

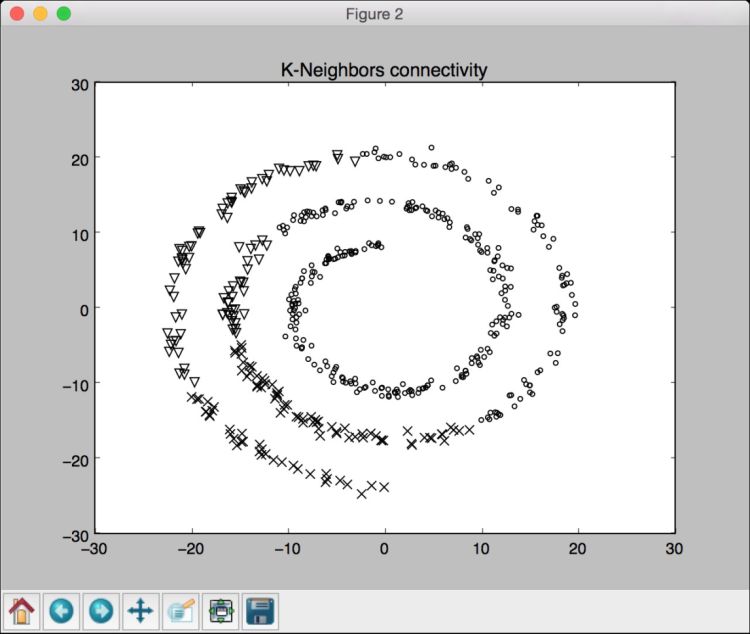
第 4 章　无监督学习——聚类 - 图9

图　4-9

从图4-8和图4-9中可以看出，使用连接特征可以让我们把连接在一起的数据合成一组，而不是按照它们在螺旋线上的位置进行聚类。

4.6　评价聚类算法的聚类效果

到目前为止，我们已经介绍了3种聚类算法，却没有度量过它们的聚类效果。在监督学习中，可以用预测值与原始值进行比较来计算模型的准确性，但是，在无监督学习中，我们的数据没有标记，因此，需要一种度量聚类算法的方法。

度量聚类算法的一个好方法是观察集群被分离的离散程度。这些集群是不是被分离得很合理？一个集群中所有的数据点是不是足够紧密？需要拟定一个指标来衡量这种特征，于是，我们采用一个被称为轮廓系数（Silhouette Coefficient）得分的指标。该得分是为每个数据点定义的，它的定义如下：

得分 = (x – y) / max(x, y)

其中，x 表示在同一个集群中某个数据点与其他数据点的平均距离，y 表示某个数据点与最近的另一个集群的所有点的平均距离。

详细步骤

(1) 本例的完整代码已经放在performance.py文件中。我们看看它是如何实现的。首先创建一个新的Python文件，然后导入一些需要用到的程序包：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.cluster import KMeans
import utilities

(2) 从data_perf.txt文件中加载输入数据：

# 加载数据
data = utilities.load_data('data_perf.txt')

(3) 为了确定集群的最佳数量，我们迭代一系列的值，找出其中的峰值：

scores = []
range_values = np.arange(2, 10)
for i in range_values:
    # 训练模型
    kmeans = KMeans(init='k-means++', n_clusters=i, n_init=10)
    kmeans.fit(data)
    score = metrics.silhouette_score(data, kmeans.labels_,
                metric='euclidean', sample_size=len(data))
    print "\nNumber of clusters =", i
    print "Silhouette score =", score
    scores.append(score)

(4) 画出图形并找出峰值：

# 画出得分条形图
plt.figure()
plt.bar(range_values, scores, width=0.6, color='k', align='center')
plt.title('Silhouette score vs number of clusters')
# 画出数据
plt.figure()
plt.scatter(data[:,0], data[:,1], color='k', s=30, marker='o', facecolors='none')
x_min, x_max = min(data[:, 0]) - 1, max(data[:, 0]) + 1
y_min, y_max = min(data[:, 1]) - 1, max(data[:, 1]) + 1
plt.title('Input data')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()

(5) 运行代码，可以在命令行工具中看到如图4-10所示的结果。

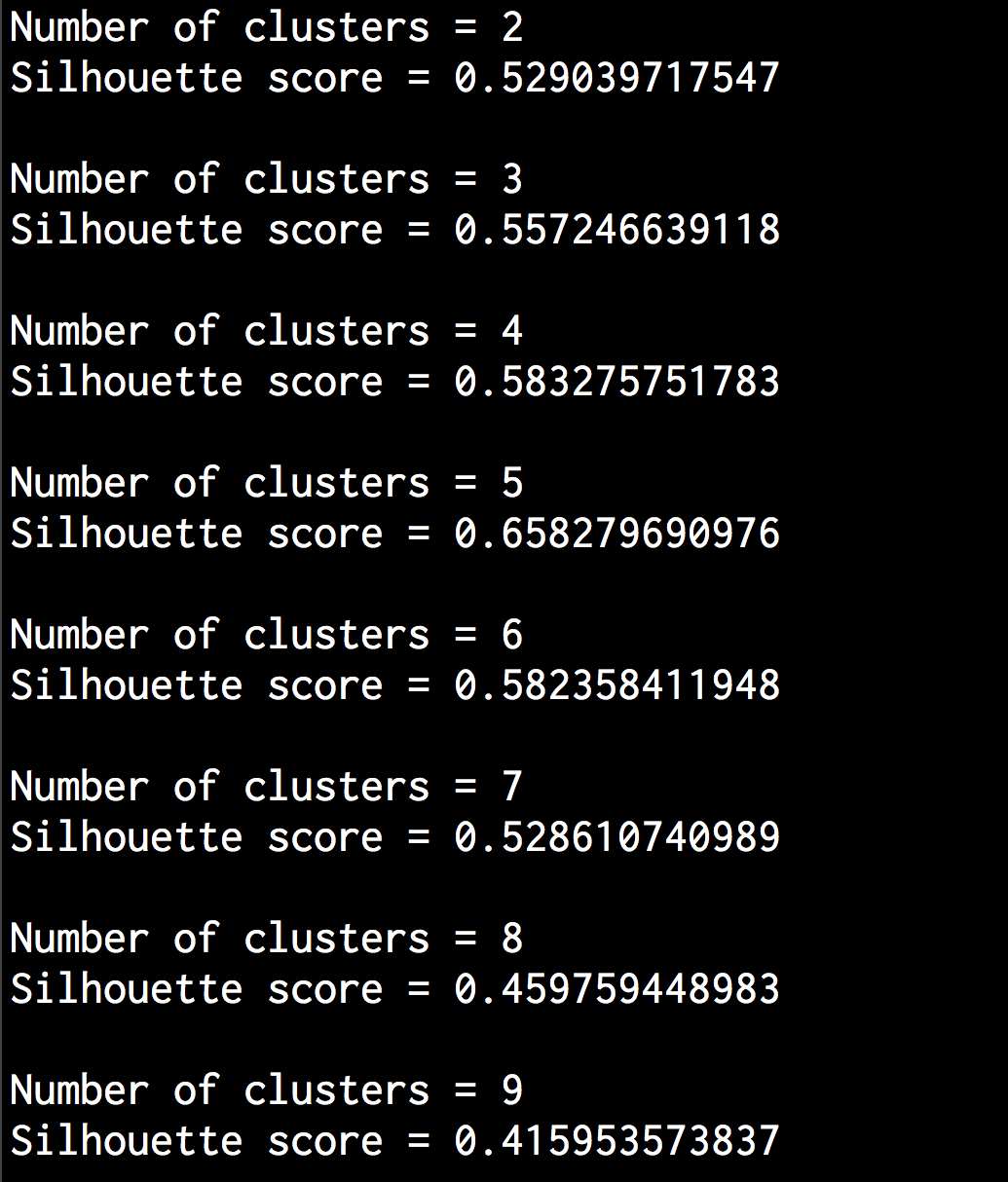
第 4 章　无监督学习——聚类 - 图10

图　4-10

(6) 画出的条形图如图4-11所示。

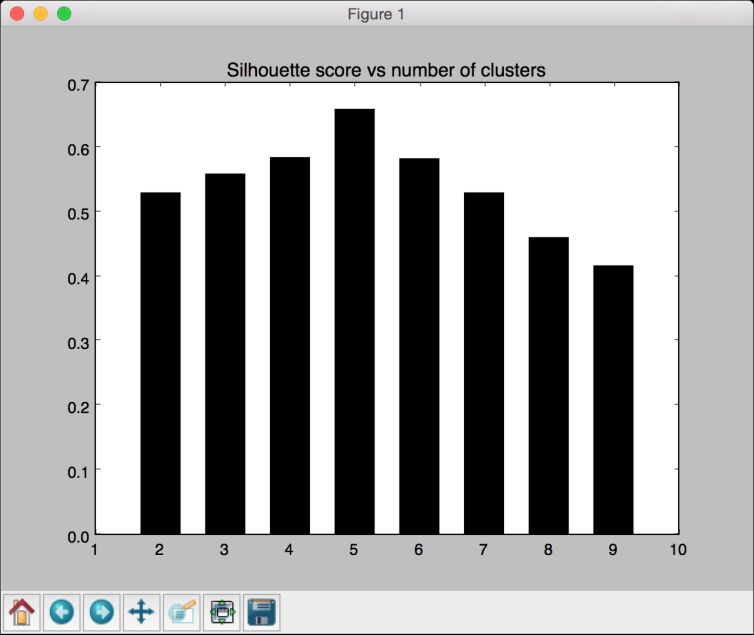
第 4 章　无监督学习——聚类 - 图11

图　4-11

(7) 从图4-11中可以看出，5个集群是最好的配置，此时的实际图形如图4-12所示。

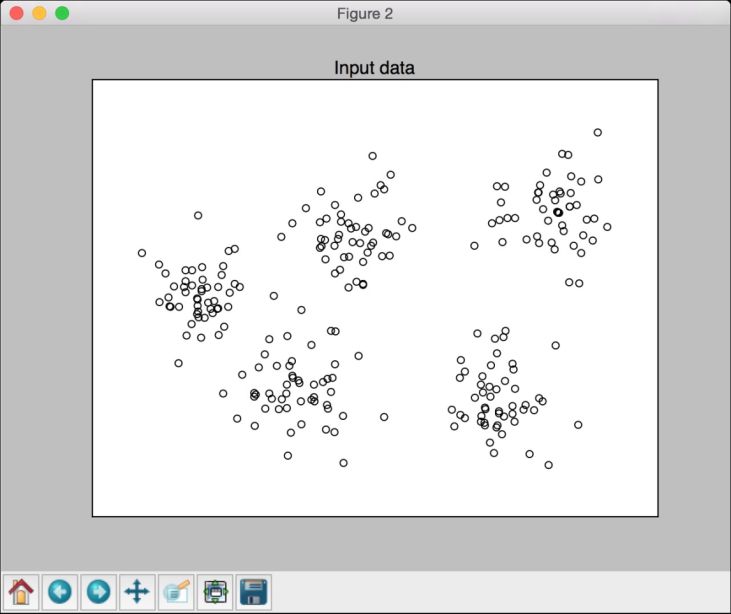
第 4 章　无监督学习——聚类 - 图12

图　4-12

可以从图4-12中直观地确认数据实际上有5个集群。我们只是采用了一个包含5个不同集群的小数据集的例子。通过轮廓系数判断聚类效果的方法，对那些包含不容易可视化的高维数据的大型数据集非常有用。

4.7　用DBSCAN算法自动估算集群数量

介绍k-means算法的时候，必须把集群数量当作一个输入参数。在真实世界中，我们事先并不知道这个信息。可以搜索集群数量的参数空间，通过轮廓系数得分找到最优的集群数量，但这是一个非常耗时的过程。难道就没有一种方法可以直接找出集群数量吗？DBSCAN（DensityBased Spatial Clustering of Applications with Noise，带噪声的基于密度的聚类方法）应运而生。

DBSCAN将数据点看成是紧密集群的若干组。如果某个点属于一个集群，那么就应该有许多点也属于同一个集群。该方法里面有一个epsilon参数，可以控制这个点到其他点的最大距离。如果两个点的距离超过了参数epsilon的值，它们就不可能在一个集群中。你可以在 http://staffwww.itn.liu.se/~aidvi/courses/06/dm/Seminars2011/DBSCAN(4).pdf.pdf)学习更多的内容。这种方法的主要优点是它可以处理异常点。如果有一些点位于数据稀疏区域，DBSCAN就会把这些点作为异常点，而不会强制将它们放入一个集群中。

详细步骤

(1) 本例的完整代码已经放在estimate_clusters.py文件中。我们看看它是如何实现的。首先创建一个新的Python文件，然后导入一些需要用到的程序库：

from itertools import cycle
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
import matplotlib.pyplot as plt
from utilities import load_data2

(2) 从data_perf.txt文件中加载输入数据。这和上一例的数据文件一样，这样可以帮助我们用同样的数据集对比两种方法：

# 加载输入数据
input_file = 'data_perf.txt'
X = load_data(input_file)

(3) 我们需要找到最佳集群数量参数。先初始化一些变量：

# 寻找最优的epsilon参数值
eps_grid = np.linspace(0.3, 1.2, num=10)
silhouette_scores = []
eps_best = eps_grid[0]
silhouette_score_max = -1
model_best = None
labels_best = None

(4) 搜索参数空间：

for eps in eps_grid:
    # 训练DBSCAN聚类模型
    model = DBSCAN(eps=eps, min_samples=5).fit(X)
    # 提取标记
    labels = model.labels_

(5) 每次迭代，我们都需要提取性能指标：

    # 提取性能指标
    silhouette_score = round(metrics.silhouette_score(X, labels), 4)
    silhouette_scores.append(silhouette_score)
    print "Epsilon:", eps, " --> silhouette score:", silhouette_score

(6) 我们需要保存指标的最佳得分和对应的epsilon值：

    if silhouette_score > silhouette_score_max:
        silhouette_score_max = silhouette_score
        eps_best = eps
        model_best = model
        labels_best = labels

(7) 画出条形图：

# 画出条形图
plt.figure()
plt.bar(eps_grid, silhouette_scores, width=0.05, color='k', align='center')
plt.title('Silhouette score vs epsilon')
# 打印最优参数
print "\nBest epsilon =", eps_best

(8) 把最优的模型和标记保存起来：

# 最优参数对应的模型与标记
model = model_best
labels = labels_best

(9) 有些数据点还没有分配集群，我们需要识别它们：

# 检查标记中没有分配集群的数据点
offset = 0
if -1 in labels:
    offset = 1

(10) 提取集群的数量：

# 数据中的集群数量
num_clusters = len(set(labels)) - offset
print "\nEstimated number of clusters =", num_clusters

(11) 提取核心样本：

# 从训练模型中提取核心样本的数据点索引
mask_core = np.zeros(labels.shape, dtype=np.bool)
mask_core[model.core_sample_indices_] = True

(12) 接下来将集群结果可视化。首先提取独特的标记集合，然后分配不同的标记：

# 画出集群结果
plt.figure()
labels_uniq = set(labels)
markers = cycle('vo^s<>')

(13) 用迭代法把每个集群的数据点用不同的标记画出来：

for cur_label, marker in zip(labels_uniq, markers):
    # 用黑点表示未分配的数据点
    if cur_label == -1:
        marker = '.'
    # 为当前标记添加符号
    cur_mask = (labels == cur_label)
    cur_data = X[cur_mask & mask_core]
    plt.scatter(cur_data[:, 0], cur_data[:, 1], marker=marker,
             edgecolors='black', s=96, facecolors='none')
    cur_data = X[cur_mask & ~mask_core]
    plt.scatter(cur_data[:, 0], cur_data[:, 1], marker=marker,
             edgecolors='black', s=32)
plt.title('Data separated into clusters')
plt.show()

(14) 运行代码，可以在命令行工具中看到如图4-13所示的结果。

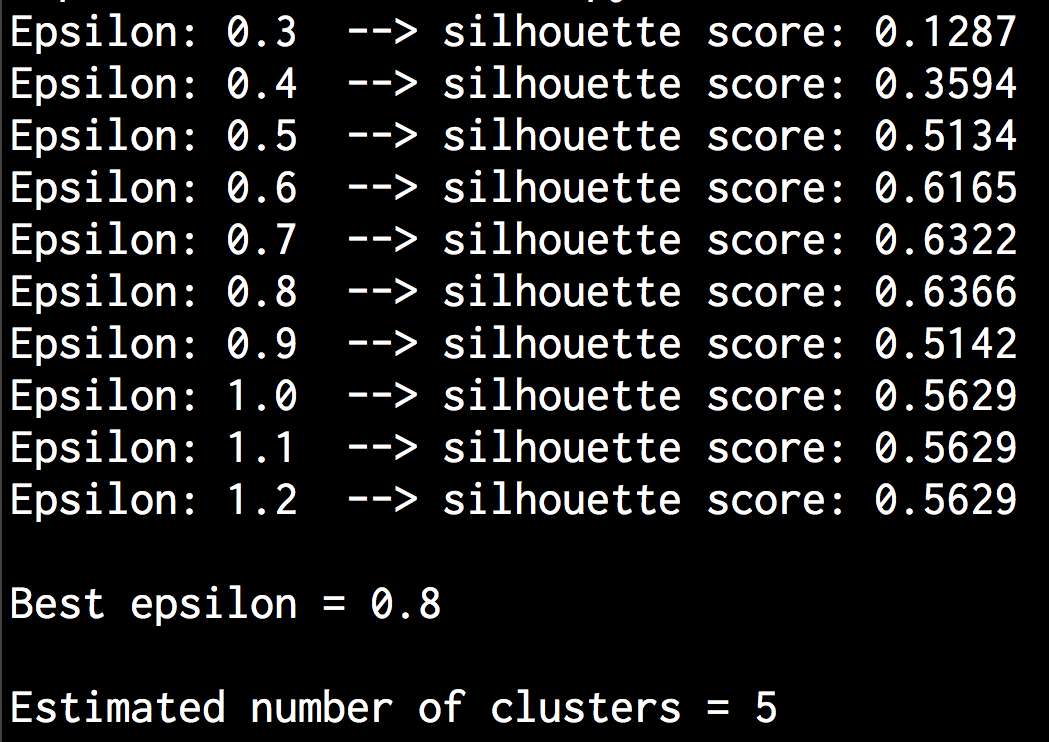
第 4 章　无监督学习——聚类 - 图13

图　4-13

(15) 条形图如图4-14所示。

{%}

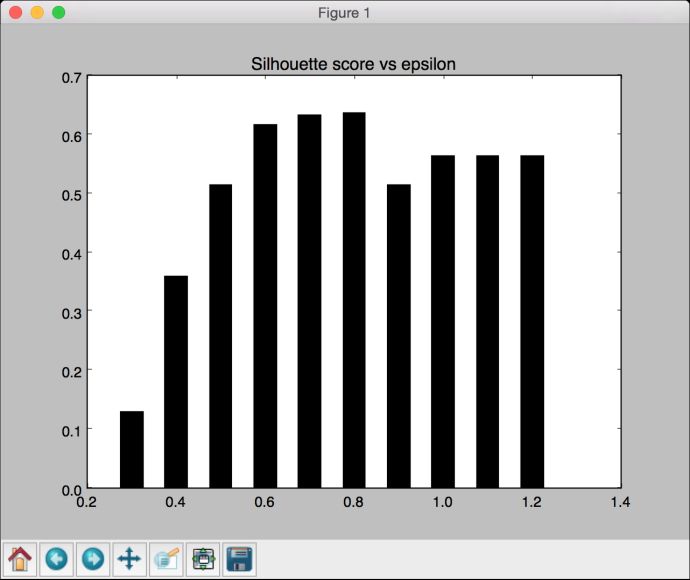
图　4-14

(16) 用实心标注的未被分配的数据点如图4-15所示。

{%}

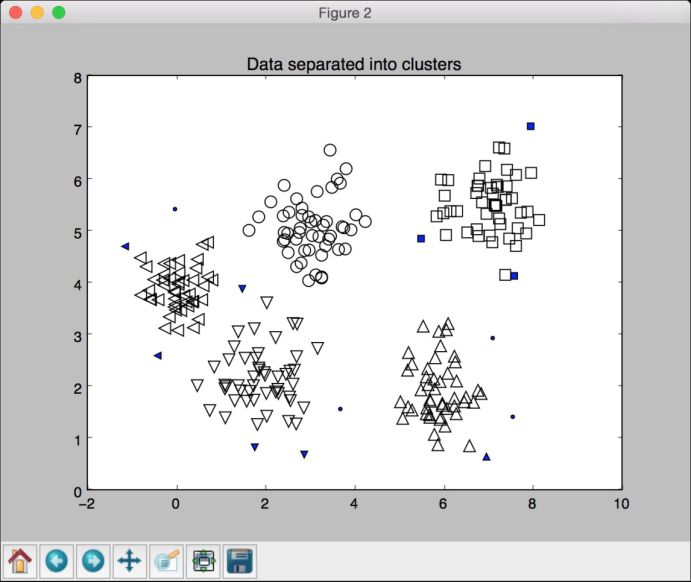
图　4-15

4.8　探索股票数据的模式

让我们看看如何用无监督学习进行股票数据分析。假设我们并不知道股票市场有多少集群，因此需要用一种近邻传播聚类（Affinity Propagation）算法来集群。这种算法会找出数据中每个集群的代表性数据点，会找到数据点间的相似性度量值，并把所有数据点看成潜在的代表性数据点，也称为取样器（exemplar）。更多内容可参考 http://www.cs.columbia.edu/~delbert/docs/DDueck-thesis_small.pdf。

本例将分析在特定时间内的股票市场变化，我们的目标是根据股价的波动找出公司行为的相似性。

详细步骤

(1) 本例的完整代码已经放在stock_market.py文件中。我们看看它是如何实现的。首先创建一个新的Python文件，然后导入一些需要用到的程序包：

import json
import datetime
import numpy as np
import matplotlib.pyplot as plt
from sklearn import covariance, cluster
from matplotlib.finance import quotes_historical_yahoo_ochl as quotes_yahoo

(2) 我们需要一个包含所有符号以及对应名称的文件，具体信息在symbol_map.json文件中。下面加载这个文件：

# 输入符号信息文件
symbol_file = 'symbol_map.json'

(3) 从符号映射文件中读取数据：

# 加载符号映射信息
with open(symbol_file, 'r') as f:
    symbol_dict = json.loads(f.read())
symbols, names = np.array(list(symbol_dict.items())).T

(4) 让我们指定分析的时间段。将用这个时间段作为输入数据的起止时间：

# 选择时间段
start_date = datetime.datetime(2004, 4, 5)
end_date = datetime.datetime(2007, 6, 2)

(5) 读取输入的数据：

quotes = [quotes_yahoo(symbol, start_date, end_date, asobject=True)
                for symbol in symbols]

(6) 由于需要分析一些特征点，我们使用每天的开盘价和收盘价的差异来分析数据：

# 提取开盘价和收盘价
opening_quotes = np.array([quote.open for quote in quotes]).astype(np.float)
closing_quotes = np.array([quote.close for quote in quotes]).astype(np.float)
# 计算每日股价波动（收盘价-开盘价）
delta_quotes = closing_quotes - opening_quotes

(7) 建立一个协方差图模型：

# 从相关性中建立协方差图模型
edge_model = covariance.GraphLassoCV()

(8) 在使用数据之前先对它进行标准化：

# 数据标准化
X = delta_quotes.copy().T
X /= X.std(axis=0)

(9) 用数据训练模型：

# 训练模型
with np.errstate(invalid='ignore'):
    edge_model.fit(X)

(10) 我们现在已经准备好建立聚类模型了：

# 用近邻传播算法建立聚类模型
, labels = cluster.affinitypropagation(edge_model.covariance_)
num_labels = labels.max()
# 打印聚类结果
for i in range(num_labels + 1):
    print "Cluster", i+1, "-->", ', '.join(names[labels == i])

运行代码，可以在命令行工具中看到如图4-16所示的结果。

{%}

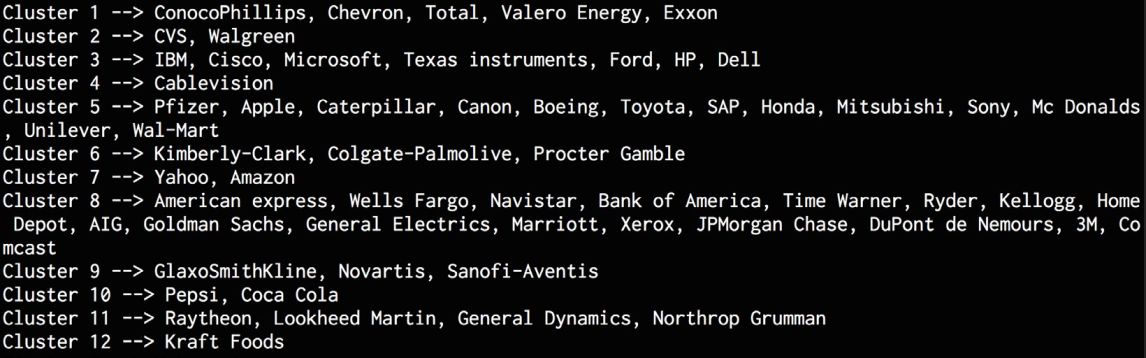
图　4-16

4.9　建立客户细分模型

无监督学习的主要应用场景之一就是市场细分。虽然在我们开发市场时获取的数据都没有标记，但是将市场细分成不同类型至关重要，这样人们就可以关注各自的市场类型了。市场细分对广告投放、库存管理、配送策略的实施、大众传媒等市场行为都非常有用。下面把无监督学习应用到一个市场细分的案例上，看看效果如何。

我们将与一个零售商和他的客户打交道，采用https://archive.ics.uci.edu/ml/datasets/Wholesale+customers的数据进行分析。数据表里包含了不同类型商品的销售数据，目标是找到数据集群，从而为客户提供最优的销售和分销策略。

详细步骤

(1) 本例的完整代码已经放在customer_segmentation.py文件中。我们看看它是如何实现的。首先创建一个新的Python文件，然后导入一些需要用到的程序包：

import csv
import numpy as np
from sklearn import cluster, covariance, manifold
from sklearn.cluster import MeanShift, estimate_bandwidth
import matplotlib.pyplot as plt

(2) 从wholesale.csv文件中加载输入数据：

# 从输入文件加载数据
input_file = 'wholesale.csv'
file_reader = csv.reader(open(input_file, 'rb'), delimiter=',')
X = []
for count, row in enumerate(file_reader):
    if not count:
        names = row[2:]
        continue
    X.append([float(x) for x in row[2:]])
# 转换为numpy数组
X = np.array(X)

(3) 和前面的内容一样，建立一个均值漂移聚类模型：

# 估计带宽参数bandwidth
bandwidth = estimate_bandwidth(X, quantile=0.8, n_samples=len(X))
# 用MeanShift函数计算聚类
meanshift_estimator = MeanShift(bandwidth=bandwidth, bin_seeding=True)
meanshift_estimator.fit(X)
labels = meanshift_estimator.labels_
centroids = meanshift_estimator.cluster_centers_
num_clusters = len(np.unique(labels))
print "\nNumber of clusters in input data =", num_clusters

(4) 打印获得的集群中心：

print "\nCentroids of clusters:"
print '\t'.join([name[:3] for name in names])
for centroid in centroids:
    print '\t'.join([str(int(x)) for x in centroid])

(5) 把两个特征（milk和groceries）的聚类结果可视化，以获取直观的输出：

# 数据可视化
centroids_milk_groceries = centroids[:, 1:3]
# 用centroids_milk_groceries中的坐标画出中心点
plt.figure()
plt.scatter(centroids_milk_groceries[:,0], centroids_milk_groceries[:,1],
        s=100, edgecolors='k', facecolors='none')
offset = 0.2
plt.xlim(centroids_milk_groceries[:,0].min() - offset * centroids_milk_groceries[:,0].ptp(),
        centroids_milk_groceries[:,0].max() + offset  centroids_milk_groceries[:,0].ptp(),)
plt.ylim(centroids_milk_groceries[:,1].min() - offset  centroids_milk_groceries[:,1].ptp(),
        centroids_milk_groceries[:,1].max() + offset * centroids_milk_groceries[:,1].ptp())
plt.title('Centroids of clusters for milk and groceries')
plt.show()

(6) 运行代码，可以在命令行工具中看到如图4-17所示的结果。

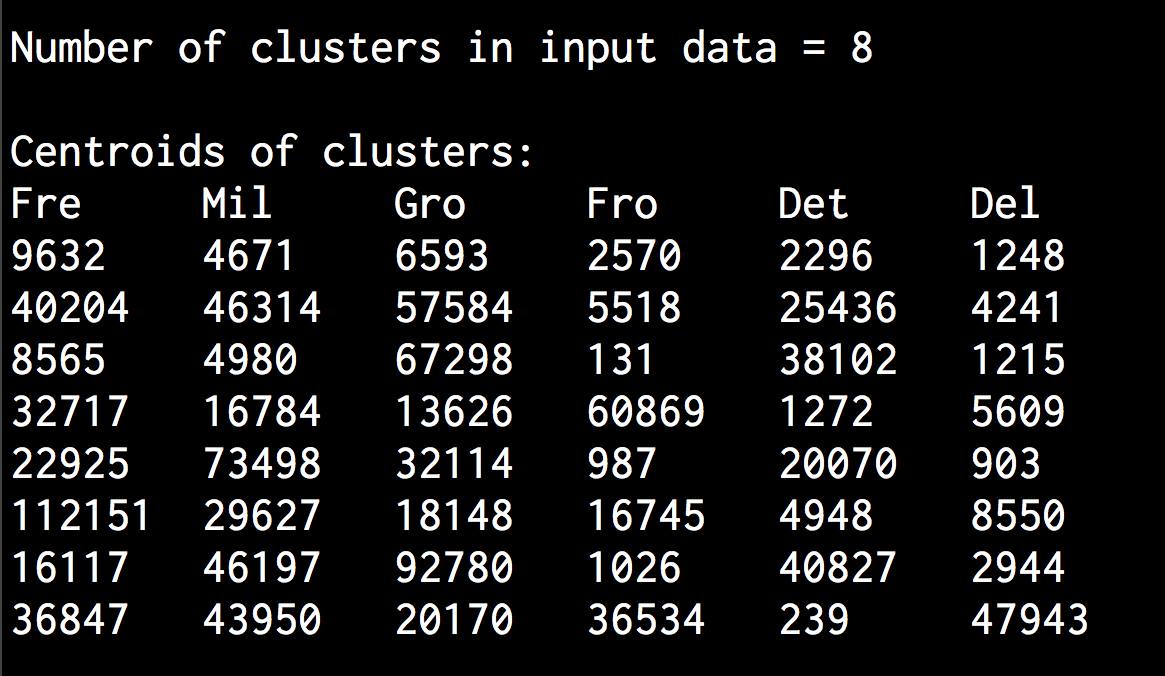
第 4 章　无监督学习——聚类 - 图17

图　4-17

(7) 如图4-18所示描绘的是milk（牛奶）和groceries（杂货）两个特征的聚类中心，其中milk特征值对应X轴坐标，groceries特征值对应Y轴坐标。

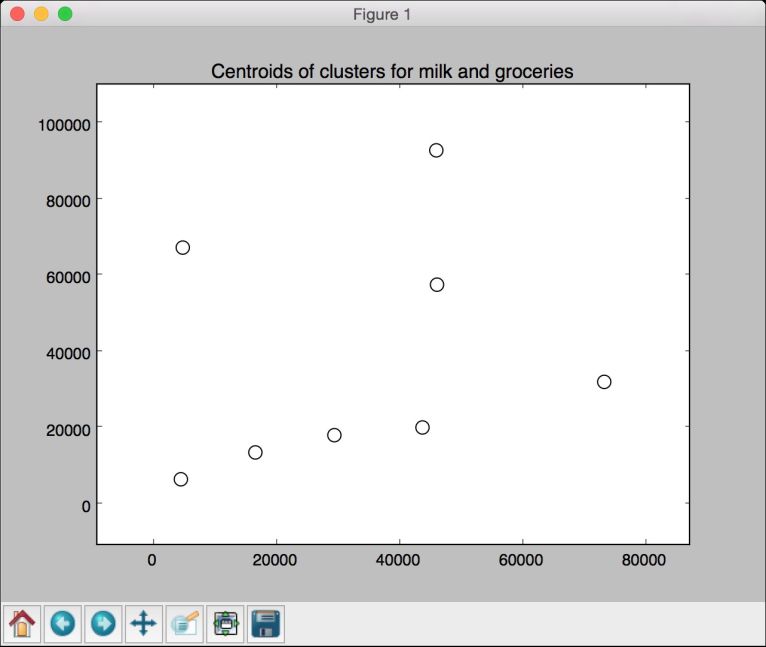
第 4 章　无监督学习——聚类 - 图18

图　4-18

第 4 章 无监督学习——聚类

第 4 章 无监督学习——聚类

4.1 简介

4.2 用k-means算法聚类数据

详细步骤

4.3 用矢量量化压缩图片

详细步骤

4.4 建立均值漂移聚类模型

详细步骤

4.5 用凝聚层次聚类进行数据分组

详细步骤

4.6 评价聚类算法的聚类效果

详细步骤

4.7 用DBSCAN算法自动估算集群数量

详细步骤

4.8 探索股票数据的模式

详细步骤

4.9 建立客户细分模型

详细步骤

第 4 章　无监督学习——聚类

第 4 章　无监督学习——聚类

4.1　简介

4.2　用k-means算法聚类数据

4.3　用矢量量化压缩图片

4.4　建立均值漂移聚类模型

4.5　用凝聚层次聚类进行数据分组

4.6　评价聚类算法的聚类效果

4.7　用DBSCAN算法自动估算集群数量

4.8　探索股票数据的模式

4.9　建立客户细分模型