第 8 章　解剖时间序列和时序数据

在这一章，我们将介绍以下主题：

  • 将数据转换为时间序列格式

  • 切分时间序列数据

  • 操作时间序列数据

  • 从时间序列数据中提取统计数字

  • 针对序列数据创建隐马尔科夫模型

  • 针对序列文本数据创建条件随机场

  • 用隐马尔科夫模型分析股票市场数据

8.1　简介

时间序列数据就是随着时间的变化收集的测量序列数据。这些数据是根据预定义的变量并在固定的间隔时间采集的。时间序列数据最主要的特征就是其顺序是非常关键的。

我们收集的数据是按照时间轴排序的，它们的出现顺序包含很多隐藏的模式和信息。如果改变顺序，则将彻底改变数据的含义。序列数据的广义概念是指任意序列形式的数据，包括时间序列数据。

我们的目标是构建一个模型，该模型描述了时间序列或任意序列的模式，用于描述时间序列模式的重要特征。可以用这些模型解释过去可能会影响到未来，查看两个数据集是如何相互关联的，如何预测未来可能的值，或者如何控制基于某个度量标准的给定变量。

为了将时间序列数据可视化，我们倾向于将其用折线图或柱状图画出。时间序列数据分析常用于金融、信号处理、天气预测、轨道预测、地震预测或者任意需要处理时间数据的场合。我们在时间序列和顺序数据分析中构建的模型应该考虑数据的顺序，并提取相互之间的关系。接下来分析Python中的时间序列和顺序数据。

8.2　将数据转换为时间序列格式

下面以理解如何将一系列观察结果转换为时间序列数据并将其可视化作为本章的开始。本例将用到pandas库来分析时间序列数据。在进行接下来的学习之前，请确保已经安装好了pandas库，安装方法可以参考http://pandas.pydata.org/pandas-docs/stable/install.htm。

详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import numpy as np
  2. import pandas as pd
  3. import matplotlib.pyplot as plt

(2) 定义一个函数来读取输入文件，该文件将序列观察结果转换为时间序列数据：

  1. def convert_data_to_timeseries(input_file, column, verbose=False):

(3) 这里将用到一个包含4列的文本文件，其中第一列表示年，第二列表示月，第三列和第四列表示数据。将文件加载到NumPy数组：

  1.     # 加载输入文件
  2.     data = np.loadtxt(input_file, delimiter=',')

(4) 因为数据是按时间的前后顺序排列的，数据的第一行是起始日期，而数据的最后一行是终止日期。下面提取出数据集的起始日期和终止日期：

  1.     # 提取起始日期和终止日期
  2.     start_date = str(int(data[0,0])) + '-' + str(int(data[0,1]))
  3.     end_date = str(int(data[-1,0] + 1)) + '-' + str(int(data[-1,1]% 12 + 1))

(5) 这个函数还有一个详细的版本。因此，当这个值为真时，就打印一些信息。打印出起始日期和终止日期：

  1.     if verbose:
  2.        print "\nStart date =", start_date
  3.        print "End date =", end_date

(6) 创建一个pandas变量，该变量包含了以月为间隔的日期序列：

  1.     # 创建以月为间隔的变量
  2.     dates = pd.date_range(start_date, end_date, freq='M')

(7) 下一步是将给定的列转换为时间序列数据。可以用年和月访问这些数据（而不是索引）：

  1.     # 将日期转换成时间序列
  2.     data_timeseries = pd.Series(data[:,column], index=dates)

(8) 打印出最开始的10个元素：

  1.     if verbose:
  2.         print "\nTime series data:\n", data_timeseries[:10]

(9) 返回时间索引变量：

  1.     return data_timeseries

(10) 定义main函数：

  1. if __name__=='__main__':

(11) 本例将使用本书提供的data_timeseries.txt文件：

  1.     # 输入数据文件
  2.     input_file = 'data_timeseries.txt'

(12) 加载文本文件的第三列，并将其转换为时间序列数据：

  1.     # 加载输入数据
  2.     column_num = 2
  3.     data_timeseries = convert_data_to_timeseries(input_file, column_num)

(13) pandas库提供了非常实用的画图功能，你可以直接在变量上运行：

  1.     # 画出数据序列数据
  2.     data_timeseries.plot()
  3.     plt.title('Input data')
  5.     plt.show()

(14) 全部代码已经包含在convert_to_timeseries.py文件中。运行该代码，可以看到如图8-1所示的图像。

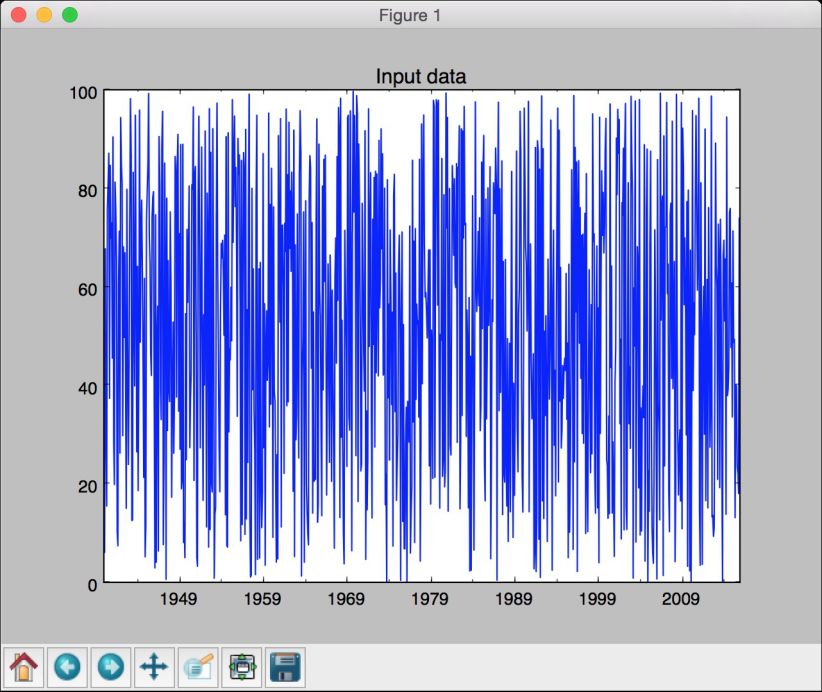
第 8 章　解剖时间序列和时序数据 - 图1

图　8-1

8.3　切分时间序列数据

这一节将介绍如何用pandas切分时间序列数据，帮助你从时间序列数据的各个阶段获得相应的信息。接下来将学习如何用日期处理数据集的子集。

详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import numpy as np
  2. import pandas as pd
  3. import matplotlib.pyplot as plt
  5. from convert_to_timeseries import convert_data_to_timeseries

(2) 使用前一节中用到的文本文件，对该文本文件中的数据进行切分：

  1. # 输入数据文件
  2. input_file = 'data_timeseries.txt'

(3) 又一次用到第三列数据：

  1. # 加载数据
  2. column_num = 2
  3. data_timeseries = convert_data_to_timeseries(input_file, column_ num)

(4) 假定我们希望提取给定的起始年份和终止年份之间的数据，下面做如下定义：

  1. # 确定画图起止年份
  2. start = '2008'
  3. end = '2015'

(5) 画出给定年份范围内的数据：

  1. plt.figure()
  2. data_timeseries[start:end].plot()
  3. plt.title('Data from ' + start + ' to ' + end)

(6) 还可以在给定月份范围内切分数据：

  1. # 画图起止年月
  2. start = '2007-2'
  3. end = '2007-11'

(7) 画出数据：

  1. plt.figure()
  2. data_timeseries[start:end].plot()
  3. plt.title('Data from ' + start + ' to ' + end)
  5. plt.show()

(8) 全部代码已经包含在slicing_data.py文件中。运行该代码，可以看到如图8-2所示的图像。

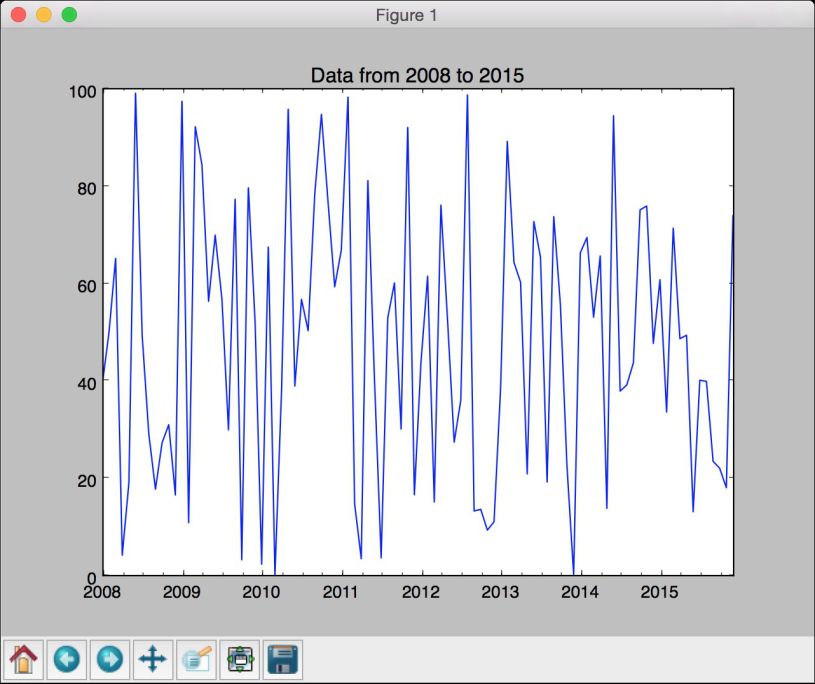
第 8 章　解剖时间序列和时序数据 - 图2

图　8-2

(9) 如图8-3所示的图像展示了更小时间范围内的数据，因此它看起来像是做了放大处理。

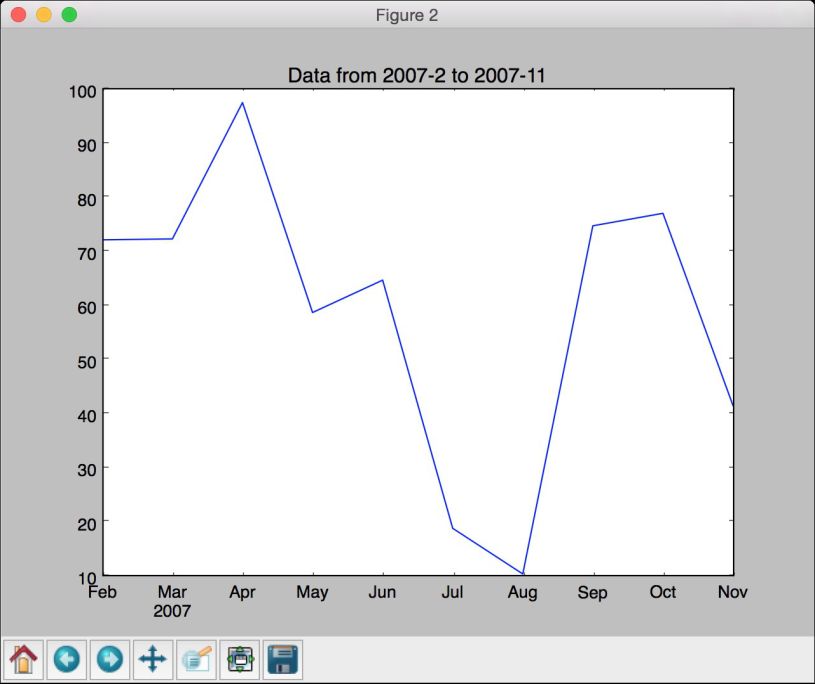
第 8 章　解剖时间序列和时序数据 - 图3

图　8-3

8.4　操作时间序列数据

现在我们知道如何切分数据并抽取各种子数据集了，接下来介绍如何操作时间序列数据。你可以用各种不同的方式过滤数据。pandas库提供了各种操作时间序列数据的方式。

详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import numpy as np
  2. import pandas as pd
  3. import matplotlib.pyplot as plt
  5. from convert_to_timeseries import convert_data_to_timeseries

(2) 使用上一节用到的文本文件：

  1. # 输入数据文件
  2. input_file = 'data_timeseries.txt'

(3) 将用到第三列和第四列数据：

  1. # 加载数据
  2. data1 = convert_data_to_timeseries(input_file, 2)
  3. data2 = convert_data_to_timeseries(input_file, 3)

(4) 将数据转化为pandas的数据帧：

  1. dataframe = pd.DataFrame({'first': data1, 'second': data2})

(5) 画出给定年份范围内的数据：

  1. # 画图
  2. dataframe['1952':'1955'].plot()
  3. plt.title('Data overlapped on top of each other')

(6) 假定我们希望画出在给定年份范围内刚才加载的两列数据的不同，可以用以下方式实现：

  1. # 画出两组数据的不同
  2. plt.figure()
  3. difference = dataframe['1952':'1955']['first'] - dataframe['1952':'1955']['second']
  4. difference.plot()
  5. plt.title('Difference (first - second)')

(7) 如果希望对第一列和第二列用不同的条件来过滤数据，可以指定这些条件并将其画出：

  1. # 当“first”大于某个阈值且“second”小于某个阈值时
  2. dataframe[(dataframe['first'] > 60) & (dataframe['second'] < 20)]. plot()
  3. plt.title('first > 60 and second < 20')
  5. plt.show()

(8) 全部代码已经包含在operating_on_data.py文件中。运行该代码，可以看到如图8-4所示的第一幅图像。

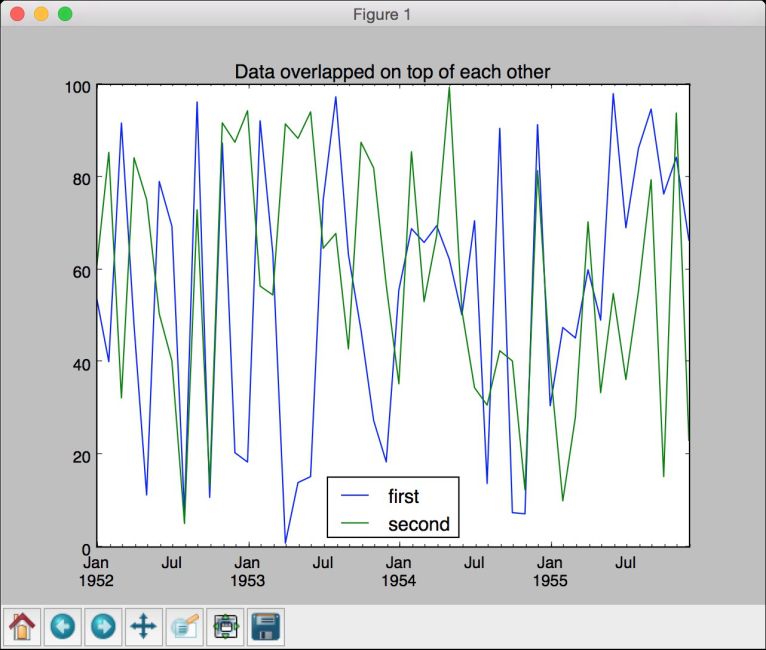
第 8 章　解剖时间序列和时序数据 - 图4

图　8-4

(9) 如图8-5所示的第二幅图像表示出不同之处。

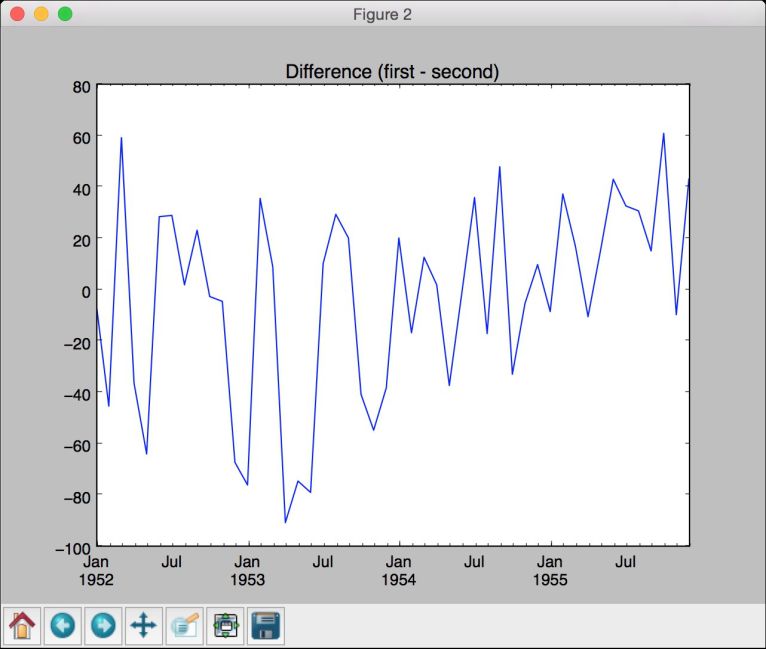
第 8 章　解剖时间序列和时序数据 - 图5

图　8-5

(10) 如图8-6所示的第三幅图像表示过滤数据。

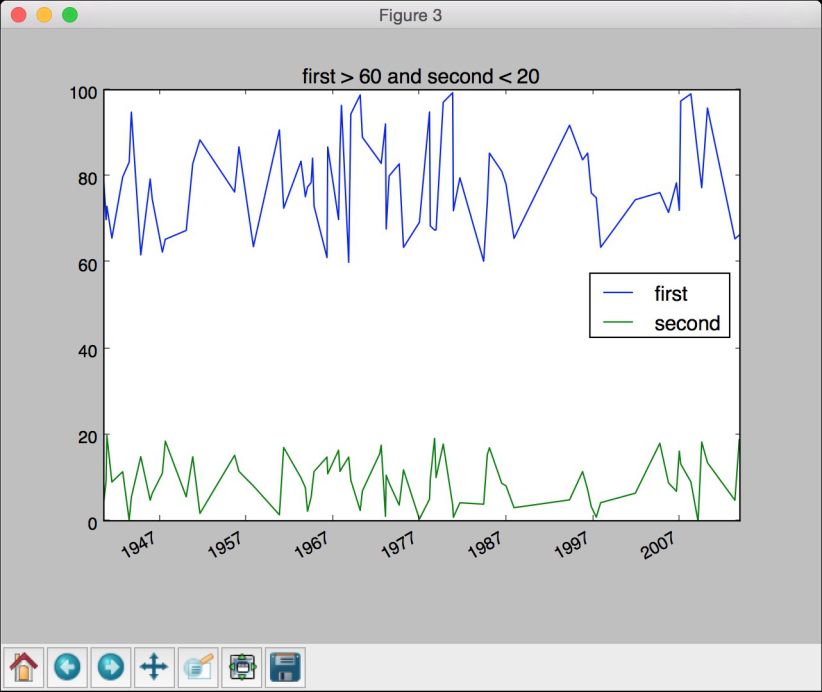
第 8 章　解剖时间序列和时序数据 - 图6

图　8-6

8.5　从时间序列数据中提取统计数字

分析时间序列数据的主要原因之一是从中提取出有趣的统计信息。考虑数据的本质，时间序列分析可以提供很多信息。本节将介绍如何提取这些统计信息。

详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import numpy as np
  2. import pandas as pd
  3. import matplotlib.pyplot as plt
  5. from convert_to_timeseries import convert_data_to_timeseries

(2) 用到前一节用到的文本文件：

  1. # 输入数据文件
  2. input_file = 'data_timeseries.txt'

(3) 加载第三列和第四列数据：

  1. # 加载数据
  2. data1 = convert_data_to_timeseries(input_file, 2)
  3. data2 = convert_data_to_timeseries(input_file, 3)

(4) 创建一个pandas数据结构来保存这些数据，这个数据看着比较像词典，它有对应的键和值：

  1. dataframe = pd.DataFrame({'first': data1, 'second': data2})

(5) 接下来提取一些统计数据。用以下代码提取最大值和最小值：

  1. #打印最大值和最小值
  2. print '\nMaximum:\n', dataframe.max()
  3. print '\nMinimum:\n', dataframe.min()

(6) 打印数据的均值或者是每行的均值：

  1. # 打印均值
  2. print '\nMean:\n', dataframe.mean()
  3. print '\nMean row-wise:\n', dataframe.mean(1)[:10]

(7) 滑动均值是在时间序列分析中较常用的统计。其最著名的应用之一是平滑信号以去除噪声。滑动均值是指计算一个窗口范围内的信号均值，并不断地移动时间窗。这里用到的窗口大小为24：

  1. # 打印滑动均值
  2. pd.rolling_mean(dataframe, window=24).plot()

(8) 相关性系数对于理解数据的本质来说非常有用：

  1. # 打印相关性系数
  2. print '\nCorrelation coefficients:\n', dataframe.corr()

(9) 用大小为60的窗口将其画出：

  1. # 画出滑动相关性
  2. plt.figure()
  3. pd.rolling_corr(dataframe['first'], dataframe['second'], window=60).plot()
  5. plt.show()

(10) 全部代码已经包含在extract_stats.py文件中。运行该代码，可以看到画出的滑动均值如图8-7所示。

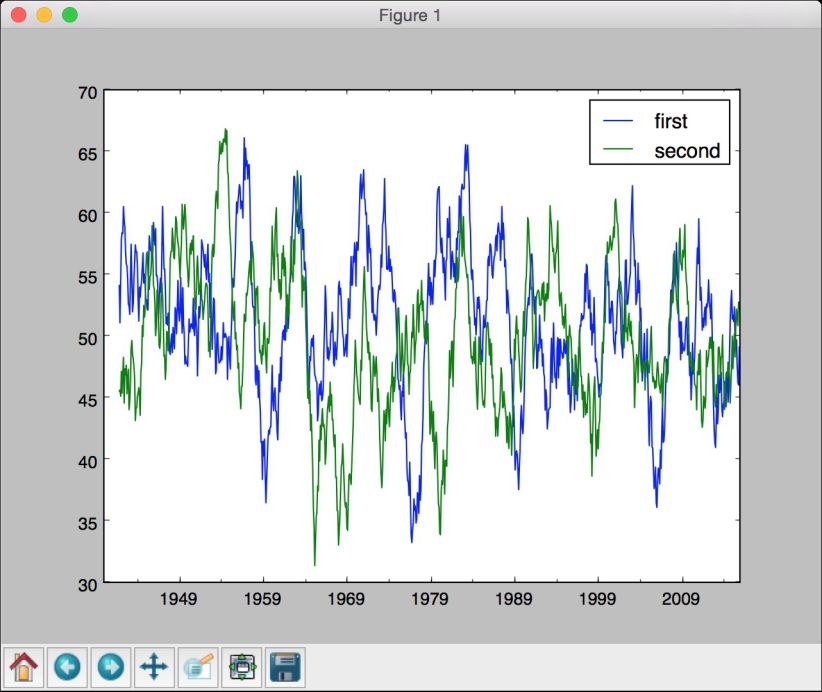
第 8 章　解剖时间序列和时序数据 - 图7

图　8-7

(11) 第二幅图像表示滑动相关性，如图8-8所示。

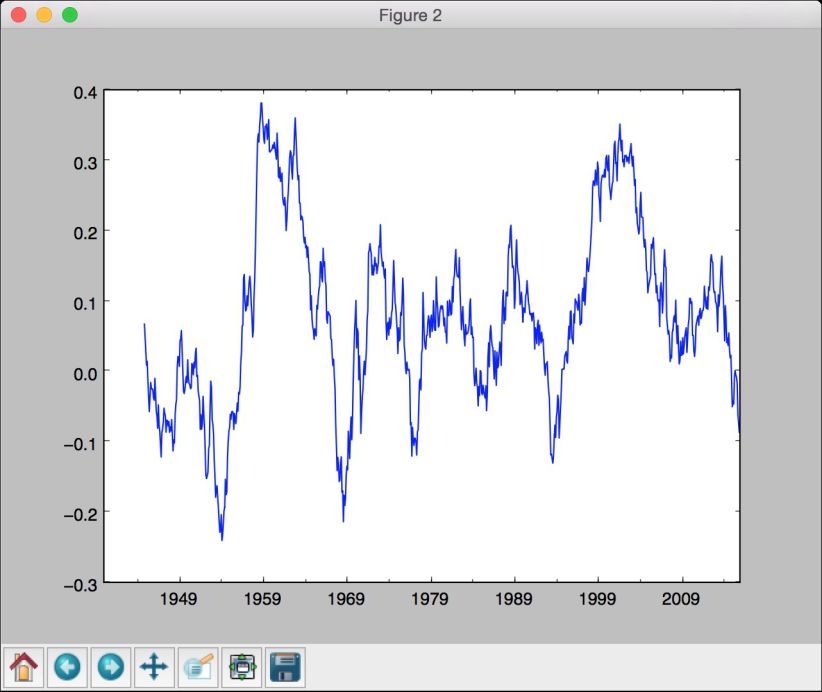
第 8 章　解剖时间序列和时序数据 - 图8

图　8-8

(12) 在命令行工具输出的上半部分，可以看到最大值、最小值和均值，如图8-9所示。

{%}

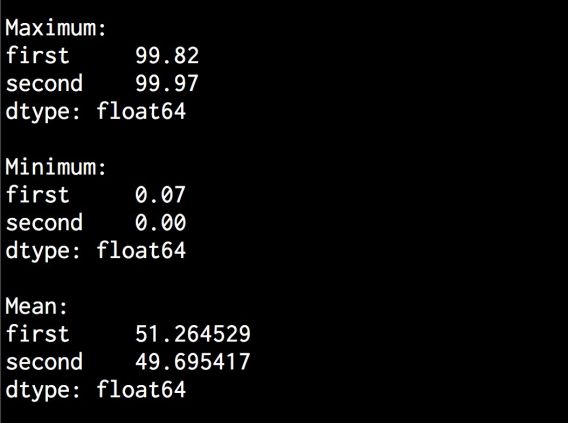
图　8-9

(13) 在命令行工具输出的下半部分，可以看到每行的均值和相关系数，如图8-10所示。

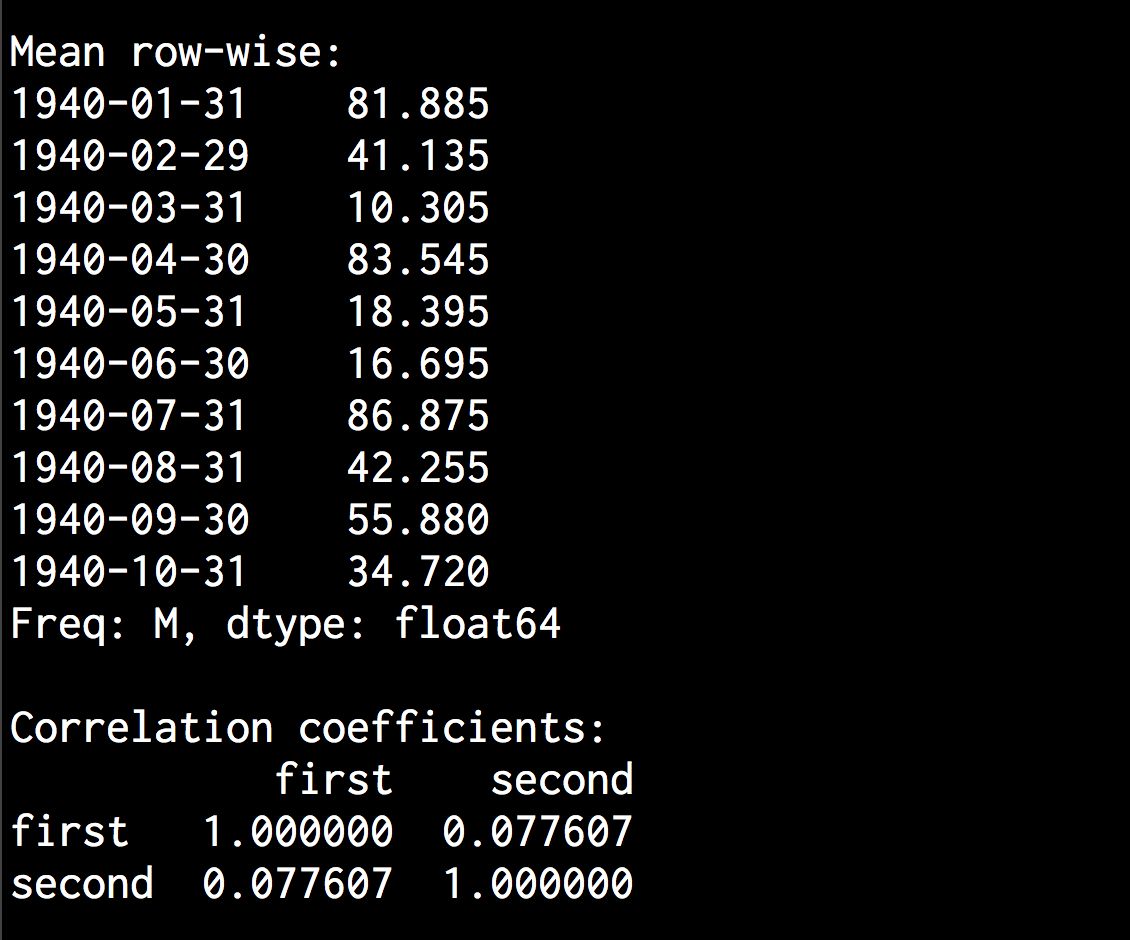
第 8 章　解剖时间序列和时序数据 - 图10

图　8-10

8.6　针对序列数据创建隐马尔科夫模型

隐马尔科夫模型（HMMs）是处理序列数据非常强大的方法，广泛应用于金融、语音分析、天气预测、单词序列等领域。我们往往对发现随时间变化的隐藏模式非常感兴趣。

任何产生输出序列的数据源均可以产生模式。请注意，HMMs是一个生成模型，这也就意味着一旦掌握了其底层结构，就可以产生数据。HMMs并不能对基础形式的类进行区分，这与那些可以做类区分的判定模型形成鲜明的对比，但是这些可以做类区分的判定模型却不能生成数据。

8.6.1　准备工作

例如，我们希望预测明天的天气是晴天、阴天或下雨。为了实现预测，需要查看所有的参数，例如温度、气压等，而潜在的状态是隐藏的。这里，潜在的状态是指3个可选状态：晴天、阴天或下雨。如果希望了解更多HMMs的详细介绍，可以在https://www.robots.ox.ac.uk/~vgg/rg/slides/hmm.pdf找到相关信息。

本例将用到hmmlearn来创建和训练HMMs，在进行接下来的学习之前，请确保你已经安装了hmmlearn，安装说明请查看http://hmmlearn.readthedocs.org/en/latest。

8.6.2　详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import datetime
  3. import numpy as np
  4. import matplotlib.pyplot as plt
  5. from hmmlearn.hmm import GaussianHMM
  7. from convert_to_timeseries import convert_data_to_timeseries

(2) 本例将用到提供的data_hmm.txt文件。该文件包括带逗号分隔符的行。每行包括3个值：一个年份、一个月份和一个浮点型数据。下面将它加载到一个NumPy数组中：

  1. # 从输入文件加载数据
  2. input_file = 'data_hmm.txt'
  3. data = np.loadtxt(input_file, delimiter=',')

(3) 将数据按照列的方向堆叠起来用于分析。我们并不需要在技术上做列堆叠，因为只有一个列，但如果你有多于一个列要进行分析，那么可以用下面的代码实现：

  1. # 排列训练数据
  2. X = np.column_stack([data[:,2]])

(4) 用4个成分创建并训练HMM。成分的个数是一个需要进行选择的超参数。这里选择4个成分，也就意味着用4个潜在状态生成数据。接下来看看这个参数的性能如何变化：

  1. # 创建并训练高斯HMM模型
  2. print "\nTraining HMM...."
  3. num_components = 4
  4. model = GaussianHMM(n_components=num_components, covariance_ type="diag", n_iter=1000)
  5. model.fit(X)

(5) 运行预测器以获得隐藏状态：

  1. # 预测HMM的隐藏状态
  2. hidden_states = model.predict(X)

(6) 计算这些隐藏状态的均值和方差：

  1. print "\nMeans and variances of hidden states:"
  2. for i in range(model.n_components):
  3.     print "\nHidden state", i+1
  4.     print "Mean =", round(model.means_[i][0], 3)
  5.     print "Variance =", round(np.diag(model.covars_[i])[0], 3)

(7) 正如前面所述，HMM是一个生成模型，因此这里生成1000个示例数据并将其画出：

  1. # 用模型生成数据
  2. num_samples = 1000
  3. samples,  = model.sample(numsamples)
  4. plt.plot(np.arange(num_samples), samples[:,0], c='black')
  5. plt.title('Number of components = ' + str(num_components))
  7. plt.show()

(8) 全部代码已经包含在hmm.py文件中。运行该代码，可以看到如图8-11所示的图像。

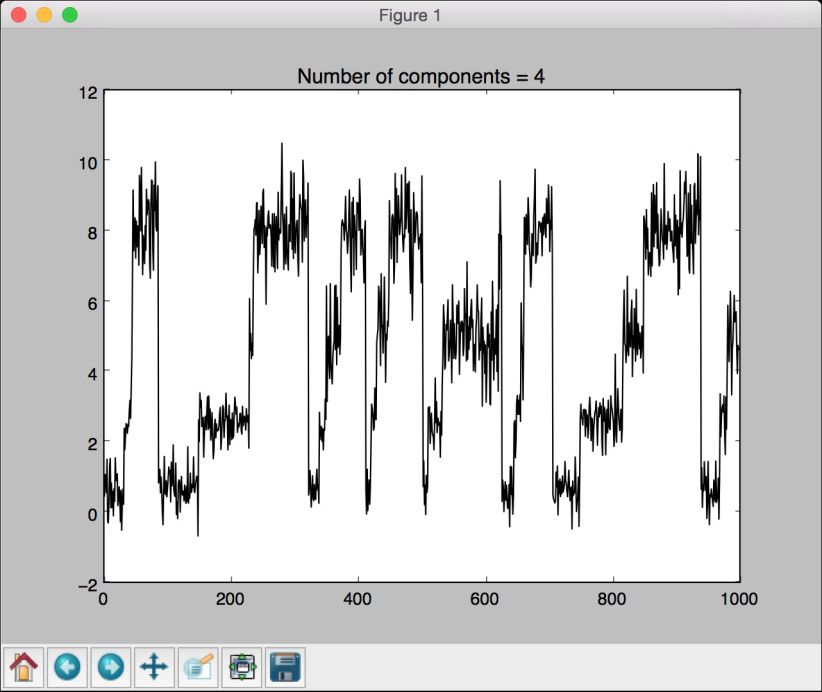
第 8 章　解剖时间序列和时序数据 - 图11

图　8-11

(9) 可以用n_components参数进行试验，看看随着其值的增加，曲线会变得更好，也可以通过设定更多的隐藏状态来训练和自定义模型。如果将这个参数设为8，其结果如图8-12所示。

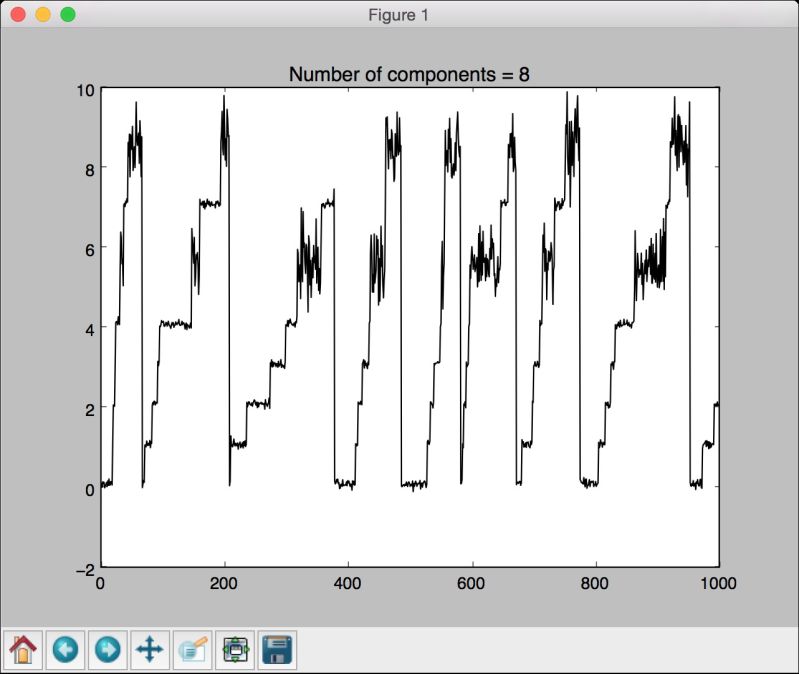
第 8 章　解剖时间序列和时序数据 - 图12

图　8-12

(10) 如果将它增加到12，图像会变得更平滑，如图8-13所示。

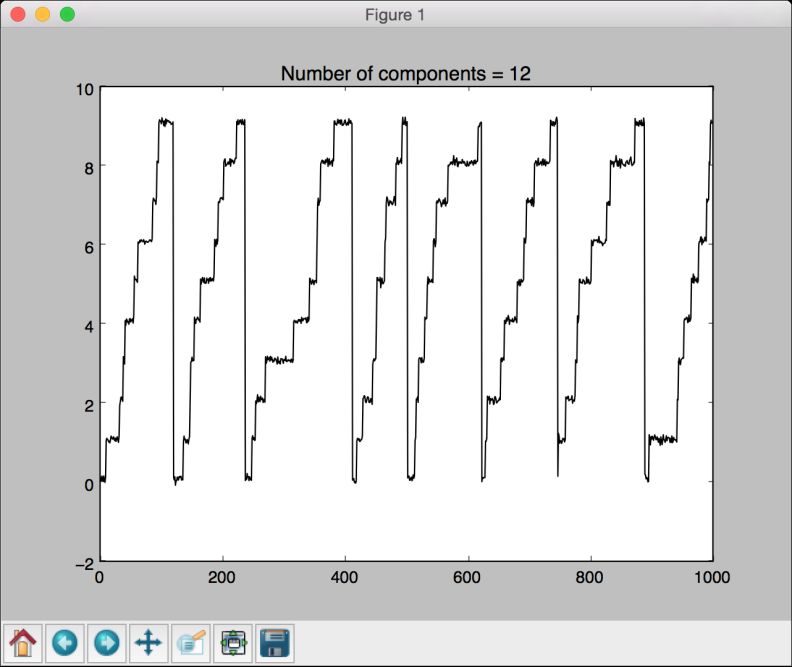
第 8 章　解剖时间序列和时序数据 - 图13

图　8-13

(11) 在命令行工具中，可以看到如图8-14所示的输出结果。

{%}

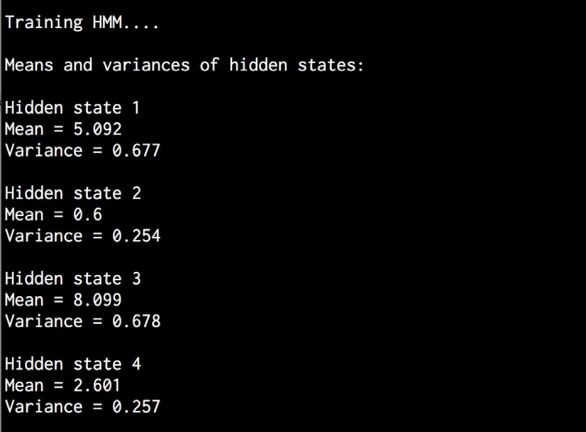
图　8-14

8.7　针对序列文本数据创建条件随机场

条件随机场（Conditional Random Fields，CRFs）是一个概率模型，该模型用于分析结构化数据。条件随机场常用于标记和分段序列数据。条件随机场与隐马尔科夫模型相反，它是一个判定模型，而隐马尔科夫模型是一个生成模型。条件随机场用于分析序列、股票、语音、单词等。在这些模型中，给定一个带标签的观察序列，对这个序列定义一个条件随机分布。这与隐马尔科夫模型相反，隐马尔科夫模型定义的是对标签和观察序列的联合分布。

8.7.1　准备工作

隐马尔科夫模型假设当前的输出是与之前的输出独立统计的。这是隐马尔科夫模型所需要的，以确保该假设能够以一种健壮的方式工作。然而，这个假设并不总是成立。时间序列中的当前输出往往取决于之前的输出。条件随机场模型优于隐马尔科夫模型的一点在于它们是由自然条件决定的，也就是说，条件随机场模型并不假设输出观察值之间的独立性。不仅如此，条件随机场还有一些优于隐马尔科夫模型的地方。条件随机场模型在诸如语言学、生物信息学、语音分析等领域的应用都优于隐马尔科夫模型。这一节将介绍如何用条件随机场模型分析字母序列。

本例将用到pystruct库来构造和训练条件随机场。在进行接下来的学习之前，请确保你已经安装了它，安装说明可查看https://pystruct.github.io/installation.html。

8.7.2　详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import os
  2. import argparse
  3. import cPickle as pickle
  5. import numpy as np
  6. import matplotlib.pyplot as plt
  7. from pystruct.datasets import load_letters
  8. from pystruct.models import ChainCRF
  9. from pystruct.learners import FrankWolfeSSVM

(2) 定义一个参数解析器，并将C值作为输入参数。C是一个超参数，该参数控制你想要的模型的具体程度，而不会失去一般化的能力：

  1. def build_arg_parser():
  2.     parser = argparse.ArgumentParser(description='Trains the CRF classifier')
  3.     parser.add_argument("--c-value", dest="c_value", required=False, type=float,
  4.             default=1.0, help="The C value that will be used for training")
  5.     return parser

(3) 定义一个处理所有与CRF相关处理的类：

  1. class CRFTrainer(object):

(4) 定义一个init函数并初始化其值：

  1.     def __init__(self, c_value, classifier_name='ChainCRF'):
  2.         self.c_value = c_value
  3.         self.classifier_name = classifier_name

(5) 下面将用链式条件随机场来分析数据。这里需要加上一个错误检查：

  1.         if self.classifier_name == 'ChainCRF':
  2.             model = ChainCRF()

(6) 定义一个在条件随机场模型中需要用到的分类器。这里用支持向量机（Support Vector Machine）来实现：

  1.             self.clf = FrankWolfeSSVM(model=model, C=self.c_value, max_iter=50)
  2.         else:
  3.             raise TypeError('Invalid classifier type')

(7) 加载字母数据集。这个数据集包括分割的字母以及和其相关的特征向量。因为已经有了特征向量，所以不需要分析图像。每个单词的首字母都已被去掉，所以剩下的字母都是小写字母：

  1.     def load_data(self):
  2.         letters = load_letters()

(8) 加载数据和标签到其相应的变量：

  1.         X, y, folds = letters['data'], letters['labels'], letters['folds']
  2.         X, y = np.array(X), np.array(y)
  3.         return X, y, folds

(9) 定义一个训练方法：

  1.     # X是由样本组成一个numpy数组，每个样本的维度是(字母, 数值)
  2.     def train(self, X_train, y_train):
  3.         self.clf.fit(X_train, y_train)

(10) 定义一个方法来评价模型的性能：

  1.     def evaluate(self, X_test, y_test):
  2.         return self.clf.score(X_test, y_test)

(11) 定义一个方法，将新数据进行分类：

  1.     # 对输入数据运行分类器
  2.     def classify(self, input_data):
  3.         return self.clf.predict(input_data)[0]

(12) 这些字母在编号的数组中被索引。为了检查输出并将其变得可读，需要将这些数字转换为字母。下面定义一个函数来执行这样的转换：

  1. def decoder(arr):
  3.     alphabets = 'abcdefghijklmnopqrstuvwxyz'
  4.     output = ''
  5.     for i in arr:
  6.         output += alphabets[i]
  8.     return output

(13) 定义main函数并解析输入参数：

  1. if __name__=='__main__':
  2.     args = build_arg_parser().parse_args()
  3.     c_value = args.c_value

(14) 用类和C值初始化变量：

  1.     crf = CRFTrainer(c_value)

(15) 加载字母数据：

  1.     X, y, folds = crf.load_data()

(16) 将数据分成训练数据集和测试数据集：

  1.     X_train, X_test = X[folds == 1], X[folds != 1]
  2.     y_train, y_test = y[folds == 1], y[folds != 1]

(17) 训练CRF模型：

  1.     print "\nTraining the CRF model..."
  2.     crf.train(X_train, y_train)

(18) 评价CRF模型的性能：

  1.     score = crf.evaluate(X_test, y_test)
  2.     print "\nAccuracy score =", str(round(score*100, 2)) + '%'

(19) 输入一个随机测试向量，并用这个模型预测输出：

  1.     print "\nTrue label =", decoder(y_test[0])
  2.     predicted_output = crf.classify([X_test[0]])
  3.     print "Predicted output =", decoder(predicted_output)

(20) 全部代码已经包含在crf.py文件中。运行该代码，可以看到在命令行工具中显示如图8-15所示的输出结果。正如你看到的，这个单词应该是“commanding”，而条件随机场模型很好地预测了这个结果。

{%}

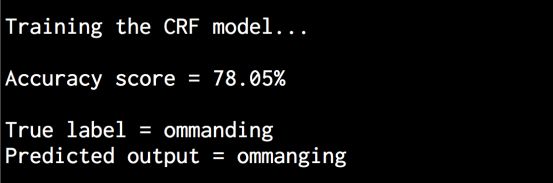
图　8-15

8.8　用隐马尔科夫模型分析股票市场数据

本节将用隐马尔科夫模型来预测股票数据。股票市场数据是典型的时间序列数据示例，其数据都是用日期格式来组织的。在即将用到的数据集中，可以看到各个公司的股票数据随时间的波动情况。隐马尔科夫模型是生成模型，可用于分析这样的时间序列数据。这一节将用这些模型分析股票价格。

详细步骤

(1) 创建一个新的Python文件，并导入以下程序包：

  1. import datetime
  3. import numpy as np
  4. import matplotlib.pyplot as plt
  5. from matplotlib.finance import quotes_historical_yahoo_ochl
  6. from hmmlearn.hmm import GaussianHMM

(2) 从雅虎财经（Yahoo finance）获取股票报价。在matplotlib库中有一个函数可以直接加载：

  1. # 从雅虎财经获取股票报价
  2. quotes = quotes_historical_yahoo_ochl("INTC", datetime.date(1994, 4, 5),
  3.          datetime.date(2015, 7, 3))

(3) 每个报价包含6个值。下面提取相关数据，如股票的收盘价和一定时期内股票的成交量：

  1. # 提取需要的数值
  2. dates = np.array([quote[0] for quote in quotes], dtype=np.int)
  3. closing_values = np.array([quote[2] for quote in quotes])
  4. volume_of_shares = np.array([quote[5] for quote in quotes])[1:]

(4) 计算每天收盘价的变化率，用这个变化率作为一个特征：

  1. # 计算每天收盘价的变化率
  2. diff_percentage = 100.0 * np.diff(closing_values) / closing_ values[:-1]
  4. dates = dates[1:]

(5) 将两个数组进行列堆叠，以用作训练：

  1. # 将变化率与交易量组合起来
  2. X = np.column_stack([diff_percentage, volume_of_shares])

(6) 用5个成分训练隐马尔科夫模型：

  1. # 创建并训练高斯HMM模型
  2. print "\nTraining HMM...."
  3. model = GaussianHMM(n_components=5, covariance_type="diag", n_ iter=1000)
  5. model.fit(X)

(7) 生成500个示例数据用于训练隐马尔科夫模型，并将其画出：

  1. # 用模型生成数据
  2. num_samples = 500
  3. samples,  = model.sample(numsamples)
  4. plt.plot(np.arange(num_samples), samples[:,0], c='black')
  6. plt.show()

(8) 全部代码已经包含在hmm_stock.py文件中。运行该代码，可以看到如图8-16所示的图像。

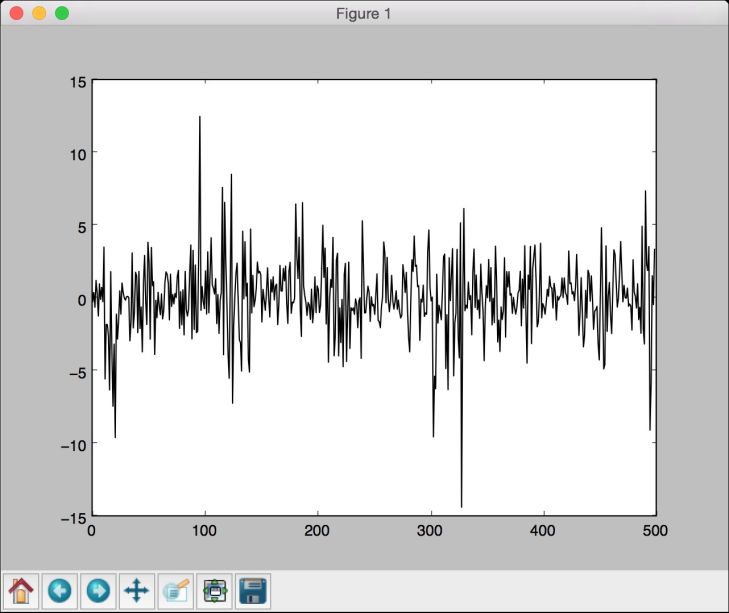
第 8 章　解剖时间序列和时序数据 - 图16

图　8-16