第 12 章　可视化数据

在这一章，我们将介绍以下主题：

  • 画3D散点图

  • 画气泡图

  • 画动态气泡图

  • 画饼图

  • 画日期格式的时间序列数据

  • 画直方图

  • 可视化热力图

  • 动态信号的可视化模拟

12.1　简介

数据可视化是机器学习的核心，利用它有助于制定正确的策略来理解数据。数据的视觉表示帮助我们选择正确的算法。数据可视化的主要目标之一就是用图和表清晰地表达出数据，以便我们更准确、更有效地交流信息。

在现实世界中总会存在各种数值数据，我们想将这些数值数据编码成图、线、点、条等，以便直观地显示这些数值中包含的信息，同时可以使复杂分布的数据更容易被理解和应用。这一过程被广泛应用于各种场合之中，包括对比分析、增长率跟踪、市场分布、民意调查等。

我们用不同的图来展示各个变量之间的模式或关系，比如用直方图展示数据的分布。如果想查找一个特定的测量，可以用表格表示。这一章将讨论各种场景下最合适的可视化方式。

12.2　画3D散点图

这一节将学习如何画3D散点图，并学习如何在三维空间中可视化这些点。

详细步骤

(1) 生成一个新的Python文件，并导入以下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from mpl_toolkits.mplot3d import Axes3D

(2) 生成一个空白图像：

  1. # 生成一个空白图像
  2. fig = plt.figure()
  3. ax = fig.add_subplot(111, projection='3d')

(3) 定义应该生成的值的个数：

  1. # 定义生成的值的个数
  2. n = 250

(4) 生成一个lambda函数来生成给定范围的值：

  1. # 生成lambda函数来生成给定范围的值
  2. f = lambda minval, maxval, n: minval + (maxval - minval) * np.random.rand(n)

(5) 用这个函数生成X、Y和Z值：

  1. # 生成值
  2. x_vals = f(15, 41, n)
  3. y_vals = f(-10, 70, n)
  4. z_vals = f(-52, -37, n)

(6) 画出这些值：

  1. # 画出这些值
  2. ax.scatter(x_vals, y_vals, z_vals, c='k', marker='o')
  3. ax.set_xlabel('X axis')
  4. ax.set_ylabel('Y axis')
  5. ax.set_zlabel('Z axis')
  7. plt.show()

(7) 全部代码已经包含在scatter_3d.py文件中。运行该代码，可以看到如图12-1所示的图像。

第 12 章　可视化数据 - 图1

图　12-1

12.3　画气泡图

下面看看如何画气泡图。在二维的气泡图中，每一个圆圈的大小表示这个点的幅值。

详细步骤

(1) 生成一个Python文件，并导入如下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt

(2) 定义要生成的值的个数：

  1. # 定义值的个数
  2. num_vals = 40

(3) 生成随机的x值和y值：

  1. # 生成随机数
  2. x = np.random.rand(num_vals)
  3. y = np.random.rand(num_vals)

(4) 在气泡图中定义每个点的面积值：

  1. # 定义每个点的面积
  2. # 指定最大半径
  3. max_radius = 25
  4. area = np.pi  (max_radius  np.random.rand(num_vals)) ** 2

(5) 定义颜色：

  1. # 生成颜色
  2. colors = np.random.rand(num_vals)

(6) 画出这些值：

  1. # 画出数据点
  2. plt.scatter(x, y, s=area, c=colors, alpha=1.0)
  4. plt.show()

(7) 全部代码已经包含在bubble_plot.py文件中。运行该代码，可以看到如图12-2所示的图像。

第 12 章　可视化数据 - 图2

图　12-2

12.4　画动态气泡图

下面来看看如何画动态气泡图。如果需要将动态的数据可视化，那就需要用到该可视化方式。

详细步骤

(1) 生成一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from matplotlib.animation import FuncAnimation

(2) 定义一个tracker函数，该函数将动态更新气泡图：

  1. def tracker(cur_num):
  2.     # 获取当前索引
  3.     cur_index = cur_num % num_points

(3) 定义颜色：

  1.     # 定义数据点颜色
  2.     datapoints['color'][:, 3] = 1.0

(4) 更新圆圈的大小：

  1.     # 更新圆圈的大小
  2.     datapoints['size'] += datapoints['growth']

(5) 更新集合中最老的数据点的位置：

  1.     # 更新集合中最老的数据点的位置
  2.     datapoints['position'][cur_index] = np.random.uniform(0, 1, 2)
  3.     datapoints['size'][cur_index] = 7
  4.     datapoints['color'][cur_index] = (0, 0, 0, 1)
  5.     datapoints['growth'][cur_index] = np.random.uniform(40, 150)

(6) 更新散点图的参数：

  1.     # 更新散点图的参数
  2.     scatter_plot.set_edgecolors(datapoints['color'])
  3.     scatter_plot.set_sizes(datapoints['size'])
  4.     scatter_plot.set_offsets(datapoints['position'])

(7) 定义main函数并生成一个空白的图像：

  1. if __name__=='__main__':
  2.     # 生成一个图像
  3.     fig = plt.figure(figsize=(9, 7), facecolor=(0,0.9,0.9))
  4.     ax = fig.add_axes([0, 0, 1, 1], frameon=False)
  5.     ax.set_xlim(0, 1), ax.set_xticks([])
  6.     ax.set_ylim(0, 1), ax.set_yticks([])

(8) 定义在任意时间点上的点的个数：

  1.     # 在随机位置创建和初始化数据点，并以随机的增长率进行初始化
  2.     num_points = 20

(9) 用随机值定义这些数据点：

  1.     datapoints = np.zeros(num_points, dtype=[('position', float, 2),
  2.             ('size', float, 1), ('growth', float, 1), ('color', float, 4)])
  3.     datapoints['position'] = np.random.uniform(0, 1, (num_points, 2))
  4.     datapoints['growth'] = np.random.uniform(40, 150, num_points)

(10) 创建一个散点图，该散点图的每一帧都会更新：

  1.     # 创建一个每一帧都会更新的散点图
  2.     scatter_plot = ax.scatter(datapoints['position'][:, 0], datapoints['position'][:, 1],
  3.                       s=datapoints['size'], lw=0.7, edgecolors=datapoints['color'],
  4.                       facecolors='none')

(11) 用tracker函数启动动态模拟：

  1.     # 用tracker函数启动动态模拟
  2.     animation = FuncAnimation(fig, tracker, interval=10)
  4.     plt.show()

(12) 全部代码已经包含在dynamic_bubble_plot.py文件中。运行该程序，可以看到如图12-3所示的图像。

{%}

图　12-3

12.5　画饼图

下面来看看如何画一个饼图。如果想将一组数据中各标签的比例值可视化展现时，可以用到该可视化方式。

详细步骤

(1) 生成一个Python文件，并导入以下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt

(2) 定义各标签和相应的值：

  1. # 按照顺时针方向定义各标签和相应的值
  2. data = {'Apple': 26,
  3.         'Mango': 17,
  4.         'Pineapple': 21,
  5.         'Banana': 29,
  6.         'Strawberry': 11}

(3) 定义可视化的颜色：

  1. # 定义可视化的颜色
  2. colors = ['orange', 'lightgreen', 'lightblue', 'gold', 'cyan']

(4) 定义一个变量，以突出饼图的一部分，将其与其他部分分离开。如果不想突出任何部分，将所有值设置为0：

  1. # 定义是否需要突出一部分
  2. explode = (0, 0, 0, 0, 0)

(5) 画饼图。注意，如果使用Python 3版本，应该在下面的函数中调用list(data.values())：

  1. # 画饼图
  2. plt.pie(data.values(), explode=explode, labels=data.keys(),
  3.         colors=colors, autopct='%1.1f%%', shadow=False, startangle=90)
  5. # 设置饼图的宽高比，“equal”表示我们希望它是圆形的
  6. plt.axis('equal')
  8. plt.show()

(6) 全部的代码已经包含在pie_chart.py文件中。运行该代码，可以看到如图12-4所示的图像。

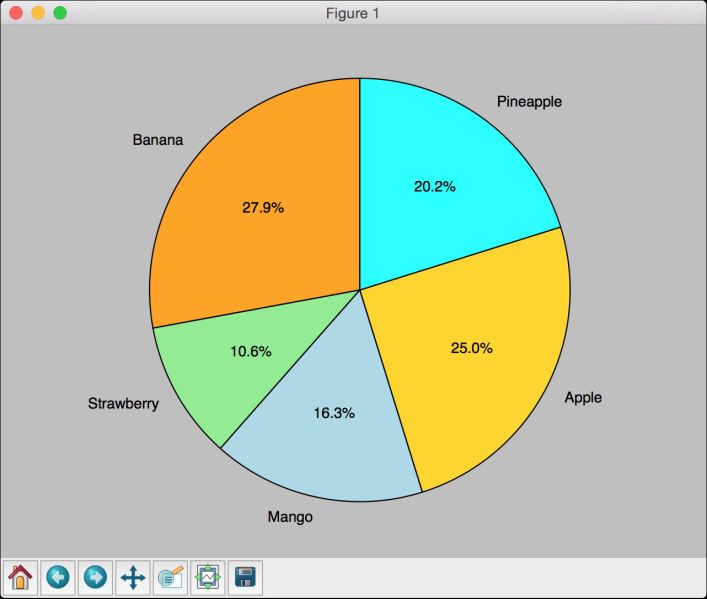
第 12 章　可视化数据 - 图4

图　12-4

如果将explode数组设置为(0, 0.2, 0, 0, 0)，那么Strawberry部分将分离突出显示，如图12-5所示。

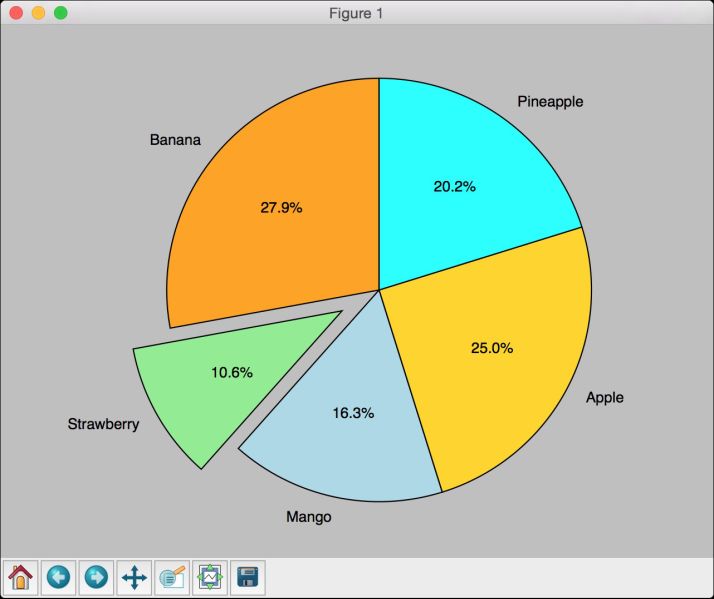
第 12 章　可视化数据 - 图5

图　12-5

12.6　画日期格式的时间序列数据

下面来看看如何用日期格式画时间序列数据。如果要将各时期的股票数据进行可视化展现，可以使用该可视化形式。

详细步骤

(1) 生成一个Python文件，并导入如下程序包：

  1. import numpy
  2. import matplotlib.pyplot as plt
  3. from matplotlib.mlab import csv2rec
  4. import matplotlib.cbook as cbook
  5. from matplotlib.ticker import Formatter

(2) 定义一个用于将日期格式化的类。init函数设置类变量：

  1. # 定义一个类将日期格式化
  2. class DataFormatter(Formatter):
  3.     def __init__(self, dates, date_format='%Y-%m-%d'):
  4.         self.dates = dates
  5.         self.date_format = date_format

(3) 提取给定时间的值，并用如下格式将其返回：

  1.     # 提取“position”位置的时间t的值
  2.     def __call__(self, t, position=0):
  3.         index = int(round(t))
  4.         if index >= len(self.dates) or index < 0:
  5.             return ''
  7.         return self.dates[index].strftime(self.date_format)

(4) 定义main函数。我们将用到matplotlib中苹果公司的股票报价CSV文件：

  1. if __name__=='__main__':
  2.     # 输入包含股价的CSV文件
  3.     input_file = cbook.get_sample_data('aapl.csv', asfileobj=False)

(5) 加载CSV文件：

  1.     # 将CSV文件加载到numpy记录数组中
  2.     data = csv2rec(input_file)

(6) 提取这些值的子集，并将其画出：

  1.     # 提取子集并画出
  2.     data = data[-70:]

(7) 创建一个格式化对象，并将其用日期数据初始化：

  1.     # 创建一个日期格式化对象
  2.     formatter = DataFormatter(data.date)

(8) 定义X轴和Y轴：

  1.     # X轴
  2.     x_vals = numpy.arange(len(data))
  4.     # Y轴表示收盘价
  5.     y_vals = data.close

(9) 画出数据：

  1.     # 画出数据
  2.     fig, ax = plt.subplots()
  3.     ax.xaxis.set_major_formatter(formatter)
  4.     ax.plot(x_vals, y_vals, 'o-')
  5.     fig.autofmt_xdate()
  6.     plt.show()

(10) 全部的代码已经包含在time_series.py文件中。运行该代码，可以看到如图12-6所示的图像。

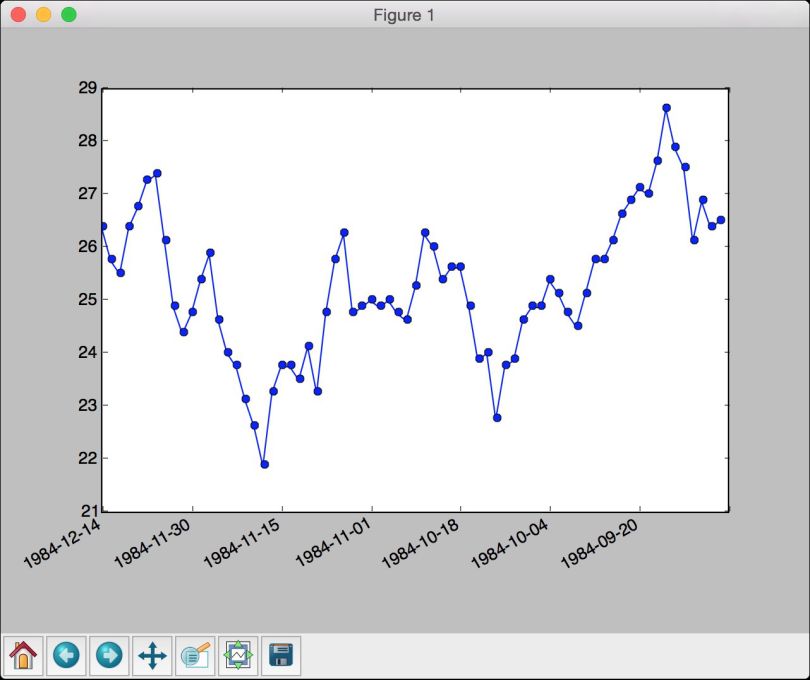
第 12 章　可视化数据 - 图6

图　12-6

12.7　画直方图

下面来看看如何画直方图。如果需要对比两组数据，可以用直方图做对比。

详细步骤

(1) 生成一个Python文件，并导入如下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt

(2) 本例对比苹果和橘子的产量，定义如下数据：

  1. # 输入数据
  2. apples = [30, 25, 22, 36, 21, 29]
  3. oranges = [24, 33, 19, 27, 35, 20]
  5. # 设置组数
  6. num_groups = len(apples)

(3) 创建一个图像并定义其参数：

  1. # 创建图像
  2. fig, ax = plt.subplots()
  4. # 定义X轴
  5. indices = np.arange(num_groups)
  7. # 直方图的宽度和透明度
  8. bar_width = 0.4
  9. opacity = 0.6

(4) 画直方图：

  1. # 画直方图
  2. hist_apples = plt.bar(indices, apples, bar_width,
  3.         alpha=opacity, color='g', label='Apples')
  5. hist_oranges = plt.bar(indices + bar_width, oranges, bar_width,
  6.         alpha=opacity, color='b', label='Oranges')

(5) 设置直方图的参数：

  1. plt.xlabel('Month')
  2. plt.ylabel('Production quantity')
  3. plt.title('Comparing apples and oranges')
  4. plt.xticks(indices + bar_width, ('Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun'))
  5. plt.ylim([0, 45])
  6. plt.legend()
  7. plt.tight_layout()
  9. plt.show()

(6) 全部的代码已经包含在histogram.py文件中。运行该代码，可以看到如图12-7所示的图像。

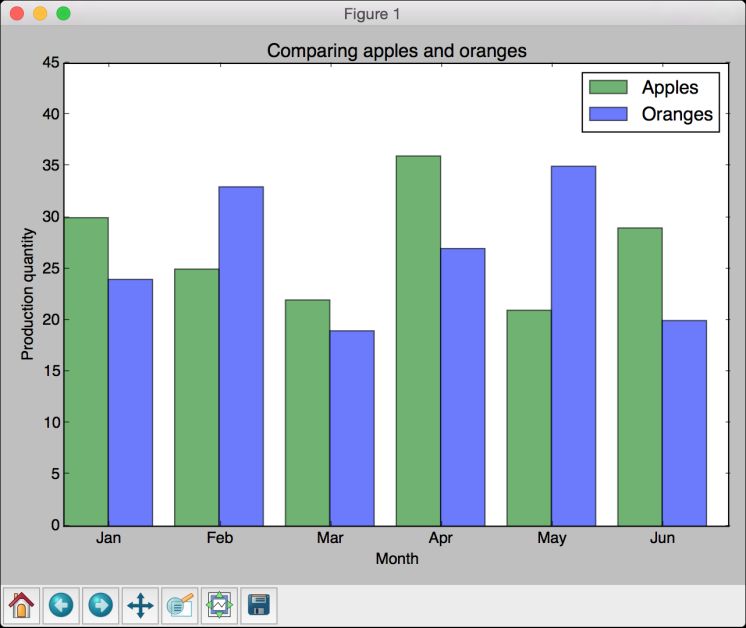
第 12 章　可视化数据 - 图7

图　12-7

12.8　可视化热力图

接下来看看如何画热力图。当两组数据的各点具有一定的相关性时，可以用这种图形表现方式。矩阵包含的单个值都被表示为图中的颜色值。

详细步骤

(1) 生成一个Python文件，并导入如下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt

(2) 定义两组数据：

  1. # 定义两组数据
  2. group1 = ['France', 'Italy', 'Spain', 'Portugal', 'Germany']
  3. group2 = ['Japan', 'China', 'Brazil', 'Russia', 'Australia']

(3) 生成一个随机二维矩阵：

  1. # 生成一些随机数
  2. data = np.random.rand(5, 5)

(4) 创建一个图像：

  1. # 创建一个图像
  2. fig, ax = plt.subplots()

(5) 创建一个热力图：

  1. # 创建一个热力图
  2. heatmap = ax.pcolor(data, cmap=plt.cm.gray)

(6) 画出这些值：

  1. # 将坐标轴放在图块的中间
  2. ax.set_xticks(np.arange(data.shape[0]) + 0.5, minor=False)
  3. ax.set_yticks(np.arange(data.shape[1]) + 0.5, minor=False)
  5. # 让热力图显示成一张表
  6. ax.invert_yaxis()
  7. ax.xaxis.tick_top()
  9. # 增加坐标轴标签
  10. ax.set_xticklabels(group2, minor=False)
  11. ax.set_yticklabels(group1, minor=False)
  13. plt.show()

(7) 全部的代码已经包含在heatmap.py文件中。运行该代码，可以看到如图12-8所示的图像。

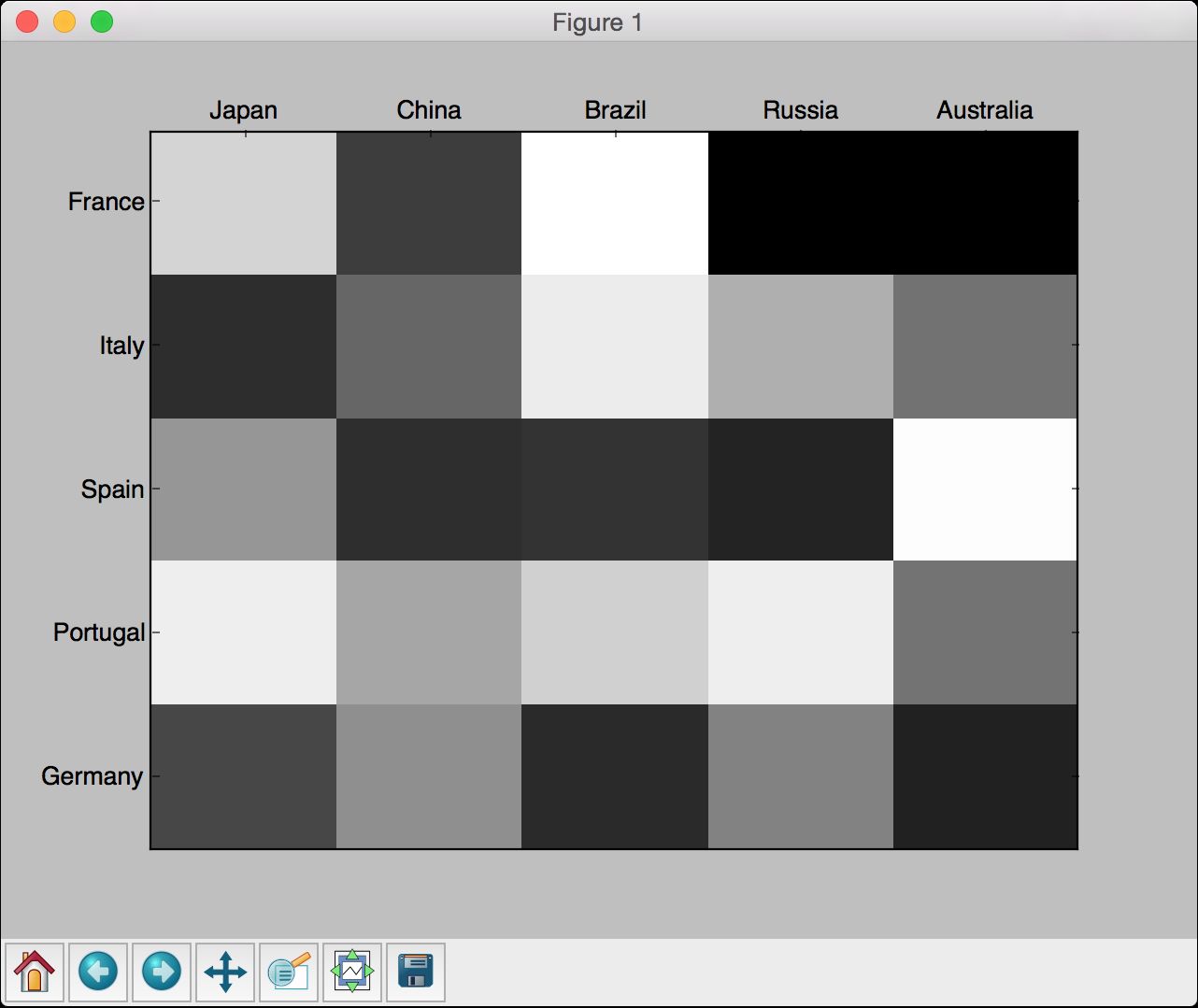
第 12 章　可视化数据 - 图8

图　12-8

12.9　动态信号的可视化模拟

如果需要将实时信号可视化，最好的方式是看到波形是如何产生的。这一节将讲解如何对实时动态变化的信号进行模拟，并将其可视化。

详细步骤

(1) 生成一个Python文件，并导入如下程序包：

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. import matplotlib.animation as animation

(2) 创建一个函数，用于生成阻尼正弦信号：

  1. # 生成信号数据
  2. def generate_data(length=2500, t=0, step_size=0.05):
  3.     for count in range(length):
  4.         t += step_size
  5.         signal = np.sin(2*np.pi*t)
  6.         damper = np.exp(-t/8.0)
  7.         yield t, signal * damper

(3) 定义一个initializer函数，用于将图像中的参数初始化：

  1. # 定义初始化函数
  2. def initializer():
  3.     peak_val = 1.0
  4.     buffer_val = 0.1

(4) 设置这些参数：

  1.     ax.set_ylim(-peak_val * (1 + buffer_val), peak_val * (1 + buffer_val))
  2.     ax.set_xlim(0, 10)
  3.     del x_vals[:]
  4.     del y_vals[:]
  5.     line.set_data(x_vals, y_vals)
  6.     return line

(5) 定义一个函数来画出这些值：

  1. def draw(data):
  2.     # 升级数据
  3.     t, signal = data
  4.     x_vals.append(t)
  5.     y_vals.append(signal)
  6.     x_min, x_max = ax.get_xlim()

(6) 如果这些值超出当前X轴最大值的范围，那么更新X轴最大值并扩展图像：

  1.     if t >= x_max:
  2.         ax.set_xlim(x_min, 2 * x_max)
  3.         ax.figure.canvas.draw()
  5.     line.set_data(x_vals, y_vals)
  7.     return line

(7) 定义main函数：

  1. if __name__=='__main__':
  2.     # 创建图形
  3.     fig, ax = plt.subplots()
  4.     ax.grid()

(8) 提取线：

  1.     # 提取线
  2.     line, = ax.plot([], [], lw=1.5)

(9) 创建变量，并用空列表对其初始化：

  1.    # 创建变量
  2.     x_vals, y_vals = [], []

(10) 用动画器对象定义并启动动画：

  1.     # 定义动画器对象
  2.     animator = animation.FuncAnimation(fig, draw, generate_data,
  3.             blit=False, interval=10, repeat=False, init_func=initializer)
  5.     plt.show()

(11) 全部的代码已经包含在moving_wave_variable.py文件中。运行该代码，可以看到如图12-9所示的图像。

第 12 章　可视化数据 - 图9

图　12-9