第 2 章　局部图像描述子

本章旨在寻找图像间的对应点和对应区域。本章将介绍用于图像匹配的两种局部描述子算法。本书的很多内容中都会用到这些局部特征，它们在很多应用中都有重要作用，比如创建全景图、增强现实技术以及计算图像的三维重建。

2.1　Harris角点检测器

Harris 角点检测算法（也称 Harris & Stephens 角点检测器）是一个极为简单的角点检测算法。该算法的主要思想是，如果像素周围显示存在多于一个方向的边，我们认为该点为兴趣点。该点就称为角点。

我们把图像域中点 x 上的对称半正定矩阵 MI=MI（x）定义为：

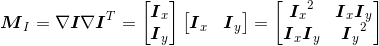\boldsymbol{M}_I=\nabla\boldsymbol{I}\nabla\boldsymbol{I}^T=\begin{bmatrix}\boldsymbol{I}_x\\\boldsymbol{I}_y\end{bmatrix}\begin{bmatrix}\boldsymbol{I}_x & \boldsymbol{I}_y\end{bmatrix}=\begin{bmatrix}{\boldsymbol{I}_x}^2 & \boldsymbol{I}_x\boldsymbol{I}_y\\\boldsymbol{I}_x\boldsymbol{I}_y & {\boldsymbol{I}_y}^2\end{bmatrix}　　　　　　(2.1)

其中 ∇I 为包含导数 Ix 和 Iy 的图像梯度（我们已经在第 1 章定义了图像的导数和梯度）。由于该定义，MI 的秩为 1，特征值为 λ1=|∇I|2 和 λ2=0。现在对于图像的每一个像素，我们可以计算出该矩阵。

选择权重矩阵 W（通常为高斯滤波器 Gσ），我们可以得到卷积：

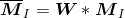\overline {\boldsymbol{M}}_I=\boldsymbol{W}*\boldsymbol{M}_I　　　　　　(2.2)

该卷积的目的是得到 MI 在周围像素上的局部平均。计算出的矩阵 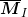\overline {\boldsymbol{M}}_I 有称为 Harris 矩阵。W 的宽度决定了在像素 x 周围的感兴趣区域。像这样在区域附近对矩阵 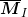\overline {\boldsymbol{M}}_I 取平均的原因是，特征值会依赖于局部图像特性而变化。如果图像的梯度在该区域变化，那么 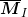\overline {\boldsymbol{M}}_I 的第二个特征值将不再为 0。如果图像的梯度没有变化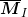，\overline {\boldsymbol{M}}_I 的特征值也不会变化。

取决于该区域∇I 的值，Harris 矩阵 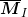\overline {\boldsymbol{M}}_I 的特征值有三种情况：

  • 如果 λ1 和 λ2 都是很大的正数，则该 x 点为角点；

  • 如果 λ1 很大，λ2 ≈ 0，则该区域内存在一个边，该区域内的平均 MI 的特征值不会变化太大；

  • 如果 λ1≈ λ2 ≈ 0，该区域内为空。

在不需要实际计算特征值的情况下，为了把重要的情况和其他情况分开，Harris 和 Stephens 在文献 [12] 中引入了指示函数：

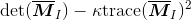
\text{det}(\overline {\boldsymbol{M}}_I)-\kappa \text{trace}(\overline {\boldsymbol{M}}_I)^2

为了去除加权常数 κ，我们通常使用商数：

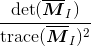
\frac {\text{det}(\overline {\boldsymbol{M}}_I)}{\text{trace}(\overline {\boldsymbol{M}}_I)^2}

作为指示器。

下面我们写出 Harris 角点检测程序。像 1.4.2 节介绍的一样，对于这个函数，我们需要使用 scipy.ndimage.filters 模块中的高斯导数滤波器来计算导数。使用高斯滤波器的道理同样是，我们需要在角点检测过程中抑制噪声强度。

首先，将角点响应函数添加到 harris.py 文件中，该函数使用高斯导数实现。同样地，参数 σ 定义了使用的高斯滤波器的尺度大小。你也可以修改这个函数，对 x 和 y 方向上不同的尺度参数，以及尝试平均操作中的不同尺度，来计算 Harris 矩阵。

  1. from scipy.ndimage import filters
  2. def compute_harris_response(im,sigma=3):
  3.   """ 在一幅灰度图像中，对每个像素计算Harris 角点检测器响应函数"""
  5.   # 计算导数
  6.   imx = zeros(im.shape)
  7.   filters.gaussian_filter(im, (sigma,sigma), (0,1), imx)
  8.   imy = zeros(im.shape)
  9.   filters.gaussian_filter(im, (sigma,sigma), (1,0), imy)
  11.   # 计算Harris 矩阵的分量
  12.   Wxx = filters.gaussian_filter(imx*imx,sigma)
  13.   Wxy = filters.gaussian_filter(imx*imy,sigma)
  14.   Wyy = filters.gaussian_filter(imy*imy,sigma)
  16.   # 计算特征值和迹
  17.   Wdet = Wxx*Wyy - Wxy**2
  18.   Wtr = Wxx + Wyy
  20.   return Wdet / Wtr

上面的函数会返回像素值为 Harris 响应函数值的一幅图像。现在，我们需要从这幅图像中挑选出需要的信息。然后，选取像素值高于阈值的所有图像点；再加上额外的限制，即角点之间的间隔必须大于设定的最小距离。这种方法会产生很好的角点检测结果。为了实现该算法，我们获取所有的候选像素点，以角点响应值递减的顺序排序，然后将距离已标记为角点位置过近的区域从候选像素点中删除。将下面的函数添加到 harris.py 文件中：

  1. def get_harris_points(harrisim,min_dist=10,threshold=0.1):
  2.   """ 从一幅Harris 响应图像中返回角点。min_dist 为分割角点和图像边界的最少像素数目"""
  4.   # 寻找高于阈值的候选角点
  5.   corner_threshold = harrisim.max()  threshold
  6.   harrisim_t = (harrisim > corner_threshold)  1
  8.   # 得到候选点的坐标
  9.   coords = array(harrisim_t.nonzero()).T
  11.   # 以及它们的Harris 响应值
  12.   candidate_values = [harrisim[c[0],c[1]] for c in coords]
  14.   # 对候选点按照Harris 响应值进行排序
  15.   index = argsort(candidate_values)
  17.   # 将可行点的位置保存到数组中
  18.   allowed_locations = zeros(harrisim.shape)
  19.   allowed_locations[min_dist:-min_dist,min_dist:-min_dist] = 1
  21.   # 按照min_distance 原则，选择最佳Harris 点
  22.   filtered_coords = []
  23.   for i in index:
  24.     if allowed_locations[coords[i,0],coords[i,1]] == 1:
  25.       filtered_coords.append(coords[i])
  26.       allowed_locations[(coords[i,0]-min_dist):(coords[i,0]+min_dist),
  27.             (coords[i,1]-min_dist):(coords[i,1]+min_dist)] = 0
  29.   return filtered_coords

现在你有了检测图像中角点所需要的所有函数。为了显示图像中的角点，你可以使用 Matplotlib 模块绘制函数，将其添加到 harris.py 文件中，如下：

  1. def plot_harris_points(image,filtered_coords):
  2.   """ 绘制图像中检测到的角点"""
  4.   figure()
  5.   gray()
  6.   imshow(image)
  7.   plot([p[1] for p in filtered_coords],[p[0] for p in filtered_coords],'*')
  8.   axis('off')
  9.   show()

试着运行下面的命令：

  1. im = array(Image.open('empire.jpg').convert('L'))
  2. harrisim = harris.compute_harris_response(im)
  3. filtered_coords = harris.get_harris_points(harrisim,6)
  4. harris.plot_harris_points(im, filtered_coords)

首先，打开该图像，转换成灰度图像。然后，计算响应函数，基于响应值选择角点。最后，在原始图像中覆盖绘制检测出的角点。绘制出的结果图像如图 2-1 所示。

第 2 章　局部图像描述子 - 图10

图 2-1：使用 Harris 角点检测器检测角点：（a）为 Harris 响应函数；（b-d）分别为使用阈值 0.01、0.05 和 0.1 检测出的角点

如果你想概要了解角点检测的不同方法，包括 Harris 角点检测器的改进和进一步的开发应用，可以查找资源，如网站 http://en.wikipedia.org/wiki/Corner_detection。

在图像间寻找对应点

Harris 角点检测器仅仅能够检测出图像中的兴趣点，但是没有给出通过比较图像间的兴趣点来寻找匹配角点的方法。我们需要在每个点上加入描述子信息，并给出一个比较这些描述子的方法。

兴趣点描述子是分配给兴趣点的一个向量，描述该点附近的图像的表观信息。描述子越好，寻找到的对应点越好。我们用对应点或者点的对应来描述相同物体和场景点在不同图像上形成的像素点。

Harris 角点的描述子通常是由周围图像像素块的灰度值，以及用于比较的归一化互相关矩阵构成的。图像的像素块由以该像素点为中心的周围矩形部分图像构成。

通常，两个（相同大小）像素块 I1(x) 和 I2(x) 的相关矩阵定义为：

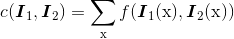
c(\boldsymbol{I}_1,\boldsymbol{I}_2)=\sum_\text{x}f(\boldsymbol{I}_1(\boldsymbol{\text{x}}),\boldsymbol{I}_2(\boldsymbol{\text{x}}))

其中，函数 f 随着相关方法的变化而变化。上式取像素块中所有像素位置 x 的和。对于互相关矩阵，函数 f(I1，I2)=I1I2,因此，c(I1，I2)=I1 · I2,其中 · 表示向量乘法（按照行或者列堆积的像素）。c(I1， I2) 的值越大，像素块 I1 和 I2 的相似度越高。1

1另一个常用的函数是 f(I1,I22)=(I1-I2)2 ，该函数表示平方差的和（Sum of Squared Difference，SSD）。

归一化的互相关矩阵是互相关矩阵的一种变形，可以定义为：

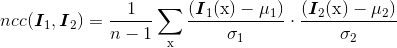ncc(\boldsymbol{I}_1,\boldsymbol{I}_2)=\frac {1}{n-1}\sum_{\text{x}}\frac{(\boldsymbol{I}_1(\boldsymbol{\text{x}} )-\mu_1)} {\sigma_1}\cdot\frac{(\boldsymbol{I}_2(\boldsymbol{\text{x}} )-\mu_2)} {\sigma_2}　　(2.3)

其中，n 为像素块中像素的数目，μ1 和 μ2 表示每个像素块中的平均像素值强度，σ1 和 σ2 分别表示每个像素块中的标准差。通过减去均值和除以标准差，该方法对图像亮度变化具有稳健性。

为获取图像像素块，并使用归一化的互相关矩阵来比较它们，你需要另外两个函数。将它们添加到 harris.py 文件中：

  1. def get_descriptors(image,filtered_coords,wid=5):
  2.   """ 对于每个返回的点，返回点周围2*wid+1 个像素的值（假设选取点的min_distance > wid）"""
  4.   desc = []
  5.   for coords in filtered_coords:
  6.     patch = image[coords[0]-wid:coords[0]+wid+1,
  7.               coords[1]-wid:coords[1]+wid+1].flatten()
  8.     desc.append(patch)
  10.   return desc
  12. def match(desc1,desc2,threshold=0.5):
  13.   """ 对于第一幅图像中的每个角点描述子，使用归一化互相关，选取它在第二幅图像中的匹配角点"""
  15.   n = len(desc1[0])
  17.   # 点对的距离
  18.   d = -ones((len(desc1),len(desc2)))
  19.   for i in range(len(desc1)):
  20.     for j in range(len(desc2)):
  21.       d1 = (desc1[i] - mean(desc1[i]))  std(desc1[i])
  22.       d2 = (desc2[j] - mean(desc2[j]))  std(desc2[j])
  23.       ncc_value = sum(d1 * d2) / (n-1)
  24.       if ncc_value > threshold:
  25.         d[i,j] = ncc_value
  27.   ndx = argsort(-d)
  28.   matchscores = ndx[:,0]
  30.   return matchscores

第一个函数的参数为奇数大小长度的方形灰度图像块，该图像块的中心为处理的像素点。该函数将图像块像素值压平成一个向量，然后添加到描述子列表中。第二个函数使用归一化的互相关矩阵，将每个描述子匹配到另一个图像中的最优的候选点。由于数值较高的距离代表两个点能够更好地匹配，所以在排序之前，我们对距离取相反数。为了获得更稳定的匹配，我们从第二幅图像向第一幅图像匹配，然后过滤掉在两种方法中不都是最好的匹配。下面的函数可以实现该操作：

  1. def match_twosided(desc1,desc2,threshold=0.5):
  2.   """ 两边对称版本的match()"""
  4.   matches_12 = match(desc1,desc2,threshold)
  5.   matches_21 = match(desc2,desc1,threshold)
  7.   ndx_12 = where(matches_12 >= 0)[0]
  9.   # 去除非对称的匹配
  10.   for n in ndx_12:
  11.     if matches_21[matches_12[n]] != n:
  12.       matches_12[n] = -1
  13. return matches_12

这些匹配可以通过在两边分别绘制出图像，使用线段连接匹配的像素点来直观地可视化。下面的代码可以实现匹配点的可视化。将这两个函数添加到 harris.py 文件中：

  1. def appendimages(im1,im2):
  2.   """ 返回将两幅图像并排拼接成的一幅新图像"""
  4.   # 选取具有最少行数的图像，然后填充足够的空行
  5.   rows1 = im1.shape[0]
  6.   rows2 = im2.shape[0]
  8.   if rows1 < rows2:
  9.     im1 = concatenate((im1,zeros((rows2-rows1,im1.shape[1]))),axis=0)
  10.   elif rows1 > rows2:
  11.     im2 = concatenate((im2,zeros((rows1-rows2,im2.shape[1]))),axis=0)
  12.   # 如果这些情况都没有，那么它们的行数相同，不需要进行填充
  14.   return concatenate((im1,im2), axis=1)
  16. def plot_matches(im1,im2,locs1,locs2,matchscores,show_below=True):
  17.   """ 显示一幅带有连接匹配之间连线的图片
  18.     输入：im1，im2（数组图像），locs1，locs2（特征位置），matchscores（match() 的输出），
  19.     show_below（如果图像应该显示在匹配的下方）"""
  21.   im3 = appendimages(im1,im2)
  22.   if show_below:
  23.     im3 = vstack((im3,im3))
  25.   imshow(im3)
  27.   cols1 = im1.shape[1]
  28.   for i,m in enumerate(matchscores):
  29.     if m>0:
  30.       plot([locs1[i][1],locs2[m][1]+cols1],[locs1[i][0],locs2[m][0]],'c')
  31.   axis('off')

图 2-2 为使用归一化的互相关矩阵（在这个例子中，每个像素块的大小为 11×11）来寻找对应点的例子。该图像可以通过下面的命令实现：

  1. wid = 5
  2. harrisim = harris.compute_harris_response(im1,5)
  3. filtered_coords1 = harris.get_harris_points(harrisim,wid+1)
  4. d1 = harris.get_descriptors(im1,filtered_coords1,wid)
  6. harrisim = harris.compute_harris_response(im2,5)
  7. filtered_coords2 = harris.get_harris_points(harrisim,wid+1)
  8. d2 = harris.get_descriptors(im2,filtered_coords2,wid)
  10. print 'starting matching'
  11. matches = harris.match_twosided(d1,d2)
  13. figure()
  14. gray()
  15. harris.plot_matches(im1,im2,filtered_coords1,filtered_coords2,matches)
  16. show()

第 2 章　局部图像描述子 - 图13

图 2-2：将归一化的互相关矩阵应用于 Harris 角点周围图像块，来寻找匹配对应点

为了看得更清楚，你可以画出匹配的子集。在上面的代码中，可以通过将数组 matches 替换成 matches[:100] 或者任意子集来实现。

如图 2-2 所示，该算法的结果存在一些不正确匹配。这是因为，与现代的一些方法相比，图像像素块的互相关矩阵具有较弱的描述性。实际运用中，我们通常使用更稳健的方法来处理这些对应匹配。这些描述符还有一个问题，它们不具有尺度不变性和旋转不变性，而算法中像素块的大小也会影响对应匹配的结果。

近年来诞生了很多用来提高特征点检测和描述性能的方法。在下一节中，我们来学习其中最好的一种算法。

2.2　SIFT（尺度不变特征变换）

David Lowe 在文献 [17] 中提出的 SIFT（Scale-Invariant Feature Transform，尺度不变特征变换）是过去十年中最成功的图像局部描述子之一。SIFT 特征后来在文献 [18] 中得到精炼并详述，经受住了时间的考验。SIFT 特征包括兴趣点检测器和描述子。SIFT 描述子具有非常强的稳健性，这在很大程度上也是 SIFT 特征能够成功和流行的主要原因。自从 SIFT 特征的出现，许多其他本质上使用相同描述子的方法也相继出现。现在，SIFT 描述符经常和许多不同的兴趣点检测器相结合使用（有些情况下是区域检测器），有时甚至在整幅图像上密集地使用。SIFT 特征对于尺度、旋转和亮度都具有不变性，因此，它可以用于三维视角和噪声的可靠匹配。你可以在 http://en.wikipedia.org/wiki/Scaleinvariant_feature_transform 获得 SIFT 特征的简要介绍。

2.2.1　兴趣点

SIFT 特征使用高斯差分函数来定位兴趣点：

D(\boldsymbol{\text{x}},\sigma)=[G_{\kappa\sigma}(\boldsymbol{\text{x}})-G_{\sigma}(\boldsymbol{\text{x}})]*\boldsymbol{I} (\boldsymbol{\text{x}})=[G_{\kappa\sigma}-G_{\sigma}]*\boldsymbol{I}=\boldsymbol{I}_{\kappa\sigma}-\boldsymbol{I}_{\sigma}

其中，Gσ 是上一章中介绍的二维高斯核，Iσ 是使用 Gσ 模糊的灰度图像，κ 是决定相差尺度的常数。兴趣点是在图像位置和尺度变化下 D(x,σ) 的最大值和最小值点。这些候选位置点通过滤波去除不稳定点。基于一些准则，比如认为低对比度和位于边上的点不是兴趣点，我们可以去除一些候选兴趣点。你可以参考文献 [17, 18] 了解更多。

2.2.2　描述子

上面讨论的兴趣点（关键点）位置描述子给出了兴趣点的位置和尺度信息。为了实现旋转不变性，基于每个点周围图像梯度的方向和大小，SIFT 描述子又引入了参考方向。SIFT 描述子使用主方向描述参考方向。主方向使用方向直方图（以大小为权重）来度量。

下面我们基于位置、尺度和方向信息来计算描述子。为了对图像亮度具有稳健性，SIFT 描述子使用图像梯度（之前 Harris 描述子使用图像亮度信息计算归一化互相关矩阵）。SIFT 描述子在每个像素点附近选取子区域网格，在每个子区域内计算图像梯度方向直方图。每个子区域的直方图拼接起来组成描述子向量。SIFT 描述子的标准设置使用 4×4 的子区域，每个子区域使用 8 个小区间的方向直方图，会产生共 128 个小区间的直方图（4×4×8=128）。图 2-3 所示为描述子的构造过程。感兴趣的读者可以参考文献 [18] 获取更多内容，或者从 http://en.wikipedia.org/wiki/Scaleinvariant_feature_transform 概要了解 SIFT 特征描述子。

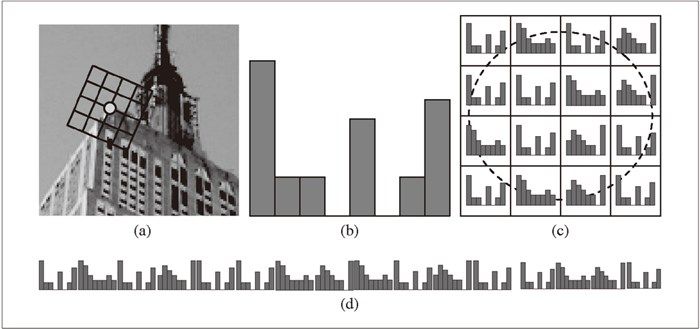
第 2 章　局部图像描述子 - 图15

图 2-3：构造 SIFT 描述子特征向量的图解：（a）一个围绕兴趣点的网格结构，其中该网格已经按照梯度主方向进行了旋转；（b）在网格的一个子区域内构造梯度方向的 8-bin 直方图；（c）在网格的每个子区域内提取直方图；（d）拼接直方图，得到一个长的特征向量

2.2.3　检测兴趣点

我们使用开源工具包 VLFeat 提供的二进制文件来计算图像的 SIFT 特征 [36]。用完整的 Python 实现 SIFT 特征的所有步骤可能效率不是很高，并且超出了本书的范围。VLFeat 工具包可以从 http://www.vlfeat.org/ 下载，二进制文件可以在所有主要的平台上运行。VLFeat 库是用 C 语言来写的，但是我们可以使用该库提供的命令行接口。如果你认为使用 Matlab 接口或者 Python 包装器比二进制文件更方便，可以从 http://github.com/mmmikael/vlfeat/ 下载相应的版本。由于 Python 包装器对平台的依赖性，安装 Python 包装器在某些平台上需要一定的技巧，所以我们这里使用二进制文件版本。Lowe 的个人网站上也有 SIFT 特征的实现，可以参见 http://www.cs.ubc.ca/~lowe/keypoints/，该代码仅适用于 Windows 系统和 Linux 系统。

创建 sift.py 文件，将下面调用可执行文件的函数添加到该文件中：

  1. def process_image(imagename,resultname,params="--edge-thresh 10 --peak-thresh 5"):
  2.   """ 处理一幅图像，然后将结果保存在文件中"""
  4.   if imagename[-3:] != 'pgm':
  5.     # 创建一个pgm 文件
  6.     im = Image.open(imagename).convert('L')
  7.     im.save('tmp.pgm')
  8.     imagename = 'tmp.pgm'
  10.   cmmd = str("sift "+imagename+" --output="+resultname+
  11.         " "+params)
  12.   os.system(cmmd)
  13.   print 'processed', imagename, 'to', resultname

由于该二进制文件需要的图像格式为灰度 .pgm，所以如果图像为其他格式，我们需要首先将其转换成 .pgm 格式文件。转换的结果以易读的格式保存在文本文件中。文本文件如下：

  1. 318.861 7.48227 1.12001 1.68523 0 0 0 1 0 0 0 0 0 11 16 0 ...
  2. 318.861 7.48227 1.12001 2.99965 11 2 0 0 1 0 0 0 173 67 0 0 ...
  3. 54.2821 14.8586 0.895827 4.29821 60 46 0 0 0 0 0 0 99 42 0 0 ...
  4. 155.714 23.0575 1.10741 1.54095 6 0 0 0 150 11 0 0 150 18 2 1 ...
  5. 42.9729 24.2012 0.969313 4.68892 90 29 0 0 0 1 2 10 79 45 5 11 ...
  6. 229.037 23.7603 0.921754 1.48754 3 0 0 0 141 31 0 0 141 45 0 0 ...
  7. 232.362 24.0091 1.0578 1.65089 11 1 0 16 134 0 0 0 106 21 16 33 ...
  8. 201.256 25.5857 1.04879 2.01664 10 4 1 8 14 2 1 9 88 13 0 0 ...
  9. …

上面数据的每一行前 4 个数值依次表示兴趣点的坐标、尺度和方向角度，后面紧接着的是对应描述符的 128 维向量。这里的描述子使用原始整数数值表示，没有经过归一化处理。当你需要比较这些描述符时，要做一些处理。更多的内容请见后面的介绍。

上面的例子显示的是在一幅图像中前 8 个特征的前面部分数值。注意前两行的坐标值相同，但是方向不同。当同一个兴趣点上出现不同的显著方向，这种情况就会出现的。

下面是如何从像上面的输出文件中，将特征读取到 NumPy 数组中的函数。将该函数添加到 sift.py 文件中：

  1. def read_features_from_file(filename):
  2.   """ 读取特征属性值，然后将其以矩阵的形式返回"""
  4.   f = loadtxt(filename)
  5.   return f[:,:4],f[:,4:] # 特征位置，描述子

在上面的函数中，我们使用 NumPy 库中的 loadtxt() 函数来处理所有的工作。

如果在 Python 会话中修改描述子，你需要将输出结果保存到特征文件中。下面的函数使用 NumPy 库中的 savetxt() 函数，可以帮你实现该功能：

  1. def write_features_to_file(filename,locs,desc):
  2.   """ 将特征位置和描述子保存到文件中"""
  3.   savetxt(filename,hstack((locs,desc)))

上面的函数使用了 hstack() 函数。该函数通过拼接不同的行向量来实现水平堆叠两个向量的功能。在这个例子中，每一行中前几列为位置信息，紧接着是描述子。

读取特征后，通过在图像上绘制出它们的位置，可以将其可视化。将下面的 plot_features() 函数添加到 sift.py 文件中，可以实现该功能。

  1. def plot_features(im,locs,circle=False):
  2.   """ 显示带有特征的图像
  3.     输入：im（数组图像），locs（每个特征的行、列、尺度和方向角度）"""
  5.   def draw_circle(c,r):
  6.     t = arange(0,1.01,.01)*2*pi
  7.     x = r*cos(t) + c[0]
  8.     y = r*sin(t) + c[1]
  9.     plot(x,y,'b',linewidth=2)
  11.   imshow(im)
  12.   if circle:
  13.     for p in locs:
  14.       draw_circle(p[:2],p[2])
  15.   else:
  16.     plot(locs[:,0],locs[:,1],'ob')
  17.   axis('off')

该函数在原始图像上使用蓝色的圆圈绘制出 SIFT 特征点的位置。将参数 circle 的选项设置为 True，该函数将使用 draw_circle() 函数绘制出圆圈，圆圈的半径为特征的尺度。

你可以通过下面的命令绘制出如图 2-4b 中 SIFT 特征位置的图像：

  1. import sift
  3. imname = 'empire.jpg'
  4. im1 = array(Image.open(imname).convert('L'))
  5. sift.process_image(imname,'empire.sift')
  6. l1,d1 = sift.read_features_from_file('empire.sift')
  8. figure()
  9. gray()
  10. sift.plot_features(im1,l1,circle=True)
  11. show()

为了比较 Harris 角点和 SIFT 特征的不同，右图（图 2-4c）显示的是同一幅图像的 Harris 角点。你可以看到，两个算法所选择特征点的位置不同。

第 2 章　局部图像描述子 - 图16

图 2-4：对一幅图像提取 SIFT 特征。（a）SIFT 特征；（b）使用圆圈表示特征尺度的 SIFT 特征；（c）为了比较，对于同一幅图像提取 Harris 角点

2.2.4　匹配描述子

对于将一幅图像中的特征匹配到另一幅图像的特征，一种稳健的准则（同样是由 Lowe 提出的）是使用这两个特征距离和两个最匹配特征距离的比率。相比于图像中的其他特征，该准则保证能够找到足够相似的唯一特征。使用该方法可以使错误的匹配数降低。下面的代码实现了匹配函数。将 match() 函数添加到 sift.py 文件中：

  1. def match(desc1,desc2):
  2.   """ 对于第一幅图像中的每个描述子，选取其在第二幅图像中的匹配
  3.     输入：desc1（第一幅图像中的描述子），desc2（第二幅图像中的描述子）"""
  5.   desc1 = array([d/linalg.norm(d) for d in desc1])
  6.   desc2 = array([d/linalg.norm(d) for d in desc2])
  8.   dist_ratio = 0.6
  9.   desc1_size = desc1.shape
  11.   matchscores = zeros((desc1_size[0],1),'int')
  12.   desc2t = desc2.T                    # 预先计算矩阵转置
  13.   for i in range(desc1_size[0]):
  14.     dotprods = dot(desc1[i,:],desc2t) # 向量点乘
  15.     dotprods = 0.9999*dotprods
  16.     # 反余弦和反排序，返回第二幅图像中特征的索引
  17.     indx = argsort(arccos(dotprods))
  19.     # 检查最近邻的角度是否小于dist_ratio 乘以第二近邻的角度
  20.     if arccos(dotprods)[indx[0]] < dist_ratio * arccos(dotprods)[indx[1]]:
  21.     matchscores[i] = int(indx[0])
  23.   return matchscores

该函数使用描述子向量间的夹角作为距离度量。在此之前，我们需要将描述子向量归一化到单位长度 2。因为这种匹配是单向的，即我们将每个特征向另一幅图像中的所有特征进行匹配，所以我们可以先计算第二幅图像兴趣点描述子向量的转置矩阵。这样，我们就不需要对每个特征分别进行转置操作。

2对于单位向量，向量乘积（不使用 arccos() 函数）等价于标准欧式距离度量。

为了进一步增加匹配的稳健性，我们可以再反过来执行一次该步骤，用另外的方法匹配（从第二幅图像中的特征向第一幅图像中的特征匹配）。最后，我们仅保留同时满足这两种匹配准则的对应（和我们对 Harris 角点的处理方法相同）。下面的 match_twosided() 函数可以实现该操作：

  1. def match_twosided(desc1,desc2):
  2.   """ 双向对称版本的match()"""
  4.   matches_12 = match(desc1,desc2)
  5.   matches_21 = match(desc2,desc1)
  7.   ndx_12 = matches_12.nonzero()[0]
  9.   # 去除不对称的匹配
  10.   for n in ndx_12:
  11.     if matches_21[int(matches_12[n])] != n:
  12.       matches_12[n] = 0
  14.   return matches_12

为了绘制出这些匹配点，我们可以使用在 harris.py 用到的相同函数。方便起见，将 appendimages() 函数和 plot_matches() 函数复制 过来。然后，将它们添加到 sift.py 文件中。如果你喜欢，也可以通过载入 harris.py 来使用这两个函数。

图 2-5 和图 2-6 是在图像对中检测 SIFT 特征点的例子，以及通过 match_twosided() 函数返回的特征点匹配情况。

第 2 章　局部图像描述子 - 图17

图 2-5：在两幅图像间检测和匹配 SIFT 特征

第 2 章　局部图像描述子 - 图18

图 2-6：在两幅图像间检测和匹配 SIFT 特征

图 2-7 是在两幅图像中分别使用 match() 函数和 match_twosided() 函数匹配特征的另一个例子。正如你所看到的一样，使用对称（两边）匹配条件可以去除不正确的匹配，保留好的匹配（一些正确的匹配也被去除了）。

第 2 章　局部图像描述子 - 图19

图 2-7：在两幅图像间匹配 SIFT 特征的例子：（a）不使用两边匹配函数，将左边图像中的特征向右边图像中的特征匹配；（b）使用两边匹配函数后，剩余的匹配情况

通过检测和匹配特征点，我们可以将这些局部描述子应用到很多例子中。为了稳健地过滤掉这些不正确的匹配，接下来的两个章节将会在对应上加入几何学的约束关系，并将局部描述子应用到一些例子中，比如自动创建全景图、照相机姿态估计以及三维结构计算。

2.3　匹配地理标记图像

我们将通过一个示例应用来结束本章节。在这个例子中，我们使用局部描述子来匹配带有地理标记的图像。**

2.3.1　从Panoramio下载地理标记图像

你可以从谷歌提供的照片共享服务 Panoramio（http://www.panoramio.com/）获得地理标记图像。像许多网络资源一样，Panoramio 提供一个 API 接口，方便用户使用程序访问这些内容。Panoramio 的 API 非常简单直接，可以在 http://www.panoramio.com/api/ 上找到 API 的使用方式。你可以通过 HTTP GET 方式访问网址内容，如下：

  1. http://www.panoramio.com/map/get_panoramas.php?order=popularity&set=public&from=0&to=20&minx=-180&miny=-90&maxx=180&maxy=90&size=medium

其中的 minx、miny、maxx 和 maxy 定义了选取照片的地理区域位置（分别表示最小经度、最小纬度、最大经度和最大纬度），你会得到可以简单解析的 JSON 格式的响应。JSON 是用于网络服务间数据传输的常用格式，比 XML 和其他格式更轻便。你可以从 http://en.wikipedia.org/wiki/JSON 获取更多关于 JSON 的内容。

你可以使用两个不同的视点来看华盛顿白宫的位置，通常从宾夕法尼亚大街南侧拍摄，或者从北侧拍摄。其坐标（纬度、经度）如下：

  1. lt=38.897661
  2. ln=-77.036564

为了转换成 API 调用需要的格式，需要在这些坐标值上减去或者加上一个数值，来获得以白宫为中心的正方形范围内的所有图像。调用如下：

  1. http://www.panoramio.com/map/get_panoramas.php?order=popularity&set=public&from=0&to=20&minx=-77.037564&miny=38.896662&maxx=-77.035564&maxy=38.898662&size=medium

该调用返回在坐标边界内（±0.001）的前 20 幅图像，这些图像按照用户访问情况排序。调用的响应格式如下：

  1. { "count": 349,
  2. "photos": [{"photo_id": 7715073, "photo_title": "White House", "photo_url":
  3. "http://www.panoramio.com/photo/7715073", "photo_file_url":
  4. "http://mw2.google.com/mw-panoramio/photos/medium/7715073.jpg", "longitude":
  5. -77.036583, "latitude": 38.897488, "width": 500, "height": 375, "upload_date":
  6. "10 February 2008", "owner_id": 1213603, "owner_name": "***", "owner_url":
  7. "http://www.panoramio.com/user/1213603"}
  8. ,
  9. {"photo_id": 1303971, "photo_title": "White House balcony", "photo_url":
  10. "http://www.panoramio.com/photo/1303971", "photo_file_url":
  11. "http://mw2.google.com/mw-panoramio/photos/medium/1303971.jpg", "longitude":
  12. -77.036353, "latitude": 38.897471, "width": 500, "height": 336, "upload_date":
  13. "13 March 2007", "owner_id": 195000, "owner_name": "***", "owner_url":
  14. "http://www.panoramio.com/user/195000"}
  15. ...
  16. ]}

为了解析这个 JSON 格式的响应，我们可以使用 simplejson 工具包，可以从 http://github.com/simplejson/simplejson 下载。在项目界面上，可以看到在线的说明文档。

如果你使用的 Python 是 2.6 或之后的版本，因为在这些后来版本中已经包含 JSON 库，所以不需要使用 simplejson 工具包。如果想使用内置的 JSON 库，你只需要像这样导入即可：

  1. import json

如果你想使用上面链接中的 simplejson 工具包（速度很快，并且比内置包含更新的内容），一个非常好的办法是使用可靠的方式导入它，如下：

  1. try: import simplejson as json
  2. except ImportError: import json

下面的代码将使用 Python 里的 urllib 工具包来处理请求，然后使用 simplejson 工具包解析返回结果：

  1. import os
  2. import urllib, urlparse
  3. import simplejson as json
  5. # 查询图像
  6. url = 'http://www.panoramio.com/map/get_panoramas.php?order=popularity&\
  7.     set=public&from=0&to=20&minx=-77.037564&miny=38.896662&\
  8.     maxx=-77.035564&maxy=38.898662&size=medium'
  9. c = urllib.urlopen(url)
  11. # 从JSON 中获得每个图像的url
  12. j = json.loads(c.read())
  13. imurls = []
  14. for im in j['photos']:
  15.     imurls.append(im['photo_file_url'])
  17. # 下载图像
  18. for url in imurls:
  19.     image = urllib.URLopener()
  20.     image.retrieve(url, os.path.basename(urlparse.urlparse(url).path))
  21.     print 'downloading:', url

通过 JSON 的输出可以看到，我们需要的是 photo_file_url 字段。运行上面的代码，在控制台上你应该能够看到类似下面的数据：

  1. downloading: http://mw2.google.com/mw-panoramio/photos/medium/7715073.jpg
  2. downloading: http://mw2.google.com/mw-panoramio/photos/medium/1303971.jpg
  3. downloading: http://mw2.google.com/mw-panoramio/photos/medium/270077.jpg
  4. downloading: http://mw2.google.com/mw-panoramio/photos/medium/15502.jpg
  5. ...

图 2-8 是本例子中返回的 20 幅图像。接下来，我们仅仅需要找到并匹配这些图像对之间的特征。

第 2 章　局部图像描述子 - 图20

图 2-8：从 panoramio.com 下载的在同一个地理位置点（以白宫为中心的方形区域）上拍摄的图像

2.3.2　使用局部描述子匹配

我们刚才已经下载了这些图像，下面需要对这些图像提取局部描述子。在这种情况下，我们将使用前面部分讲述的 SIFT 特征描述子。我们假设已经对这些图像使用 SIFT 特征提取代码进行了处理，并且将特征保存在和图像同名（但文件名后缀是 .sift，而不是 .jpg）的文件中。假设 imlist 和 featlist 列表中包含这些文件名。我们可以对所有组合图像对进行逐个匹配，如下：

  1. import sift
  3. nbr_images = len(imlist)
  5. matchscores = zeros((nbr_images,nbr_images))
  6. for i in range(nbr_images):
  7.   for j in range(i,nbr_images): # 仅仅计算上三角
  9.     print 'comparing ', imlist[i], imlist[j]
  11.     l1,d1 = sift.read_features_from_file(featlist[i])
  12.     l2,d2 = sift.read_features_from_file(featlist[j])
  14.     matches = sift.match_twosided(d1,d2)
  16.     nbr_matches = sum(matches > 0)
  17.     print 'number of matches = ', nbr_matches
  18.     matchscores[i,j] = nbr_matches
  20. # 复制值
  21. for i in range(nbr_images):
  22.   for j in range(i+1,nbr_images): # 不需要复制对角线
  23.     matchscores[j,i] = matchscores[i,j]

我们将每对图像间的匹配特征数保存在 matchscores 数组中。因为该“距离度量”是对称的，所以我们可以不在代码的最后部分复制数值，来将 matchscores 矩阵填充完整；填充完整后的 matchscores 矩阵只是看起来更好。这些特定图像的 matchscores 矩阵里的数值如下：

  1. 662 0 0 2 0 0 0 0 1 0 0 1 2 0 3 0 19 1 0 2
  2. 0 901 0 1 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 2
  3. 0 0 266 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
  4. 2 1 0 1481 0 0 2 2 0 0 0 2 2 0 0 0 2 3 2 0
  5. 0 0 0 0 1748 0 0 1 0 0 0 0 0 2 0 0 0 0 0 1
  6. 0 0 0 0 0 1747 0 0 1 0 0 0 0 0 0 0 0 1 1 0
  7. 0 0 0 2 0 0 555 0 0 0 1 4 4 0 2 0 0 5 1 0
  8. 0 1 0 2 1 0 0 2206 0 0 0 1 0 0 1 0 2 0 1 1
  9. 1 1 0 0 0 1 0 0 629 0 0 0 0 0 0 0 1 0 0 20
  10. 0 0 0 0 0 0 0 0 0 829 0 0 1 0 0 0 0 0 0 2
  11. 0 0 0 0 0 0 1 0 0 0 1025 0 0 0 0 0 1 1 1 0
  12. 1 1 0 2 0 0 4 1 0 0 0 528 5 2 15 0 3 6 0 0
  13. 2 0 0 2 0 0 4 0 0 1 0 5 736 1 4 0 3 37 1 0
  14. 0 0 1 0 2 0 0 0 0 0 0 2 1 620 1 0 0 1 0 0
  15. 3 0 0 0 0 0 2 1 0 0 0 15 4 1 553 0 6 9 1 0
  16. 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2273 0 1 0 0
  17. 19 0 0 2 0 0 0 2 1 0 1 3 3 0 6 0 542 0 0 0
  18. 1 0 0 3 0 1 5 0 0 0 1 6 37 1 9 1 0 527 3 0
  19. 0 1 0 2 0 1 1 1 0 0 1 0 1 0 1 0 0 3 1139 0
  20. 2 2 0 0 1 0 0 1 20 2 0 0 0 0 0 0 0 0 0 499

使用该 matchscores 矩阵作为图像间简单的距离度量方式（具有相似内容的图像间拥有更多的匹配特征数），下面我们可以使用相似的视觉内容来将这些图像连接起来。

2.3.3　可视化连接的图像

我们首先通过图像间是否具有匹配的局部描述子来定义图像间的连接，然后可视化这些连接情况。为了完成可视化，我们可以在图中显示这些图像，图的边代表连接。我们将会使用 pydot 工具包（http://code.google.com/p/pydot/），该工具包是功能强大的 GraphViz 图形库的 Python 接口。Pydot 使用 Pyparsing（http://pyparsing.wikispaces.com/） 和 GraphViz（http://www.graphviz.org/）；不用担心，这些都非常容易安装，只需要几分钟就可以安装成功。

Pydot 非常容易使用。下面的一小段代码很好地展示了这一点。该代码会创建一个图，该图表示深度为 2 的树，具有 5 个分支，将分支的编号添加到分支节点上。图的结构如图 2-9 所示。我们有很多方法来修改图的布局和外观。如果你想了解更多内容，可以查看 Pydot 的说明文档，或者在 http://www.graphviz.org/Documentation.php 查看 GraphViz 使用的 DOT 语言介绍。

  1. import pydot
  3. g = pydot.Dot(graph_type='graph')
  5. g.add_node(pydot.Node(str(0),fontcolor='transparent'))
  6. for i in range(5):
  7.   g.add_node(pydot.Node(str(i+1)))
  8.   g.add_edge(pydot.Edge(str(0),str(i+1)))
  9.   for j in range(5):
  10.     g.add_node(pydot.Node(str(j+1)+'-'+str(i+1)))
  11.     g.add_edge(pydot.Edge(str(j+1)+'-'+str(i+1),str(j+1)))
  12. g.write_png('graph.jpg',prog='neato')

第 2 章　局部图像描述子 - 图21

图 2-9：使用 pydot 工具包创建图

我们接下来继续探讨地理标记图像处理的例子。为了创建显示可能图像组的图，如果匹配的数目高于一个阈值，我们使用边来连接相应的图像节点。为了得到图中的图像，需要使用图像的全路径（在下面例子中，使用 path 变量表示）。为了使图像看起来漂亮，我们需要将每幅图像尺度化为缩略图形式，缩略图的最大边为 100 像素。下面是具体实现代码：

  1. import pydot
  3. threshold = 2 # 创建关联需要的最小匹配数目
  5. g = pydot.Dot(graph_type='graph') # 不使用默认的有向图
  6. for i in range(nbr_images):
  7.   for j in range(i+1,nbr_images):
  8.     if matchscores[i,j] > threshold:
  9.         # 图像对中的第一幅图像
  10.         im = Image.open(imlist[i])
  11.         im.thumbnail((100,100))
  12.         filename = str(i)+'.png'
  13.         im.save(filename) # 需要一定大小的临时文件
  14.         g.add_node(pydot.Node(str(i),fontcolor='transparent',
  15.               shape='rectangle',image=path+filename))
  17.         # 图像对中的第二幅图像
  18.         im = Image.open(imlist[j])
  19.         im.thumbnail((100,100))
  20.         filename = str(j)+'.png'
  21.         im.save(filename) # 需要一定大小的临时文件
  22.         g.add_node(pydot.Node(str(j),fontcolor='transparent',
  23.                 shape='rectangle',image=path+filename))
  25.         g.add_edge(pydot.Edge(str(i),str(j)))
  27.   g.write_png('whitehouse.png')

代码运行结果如图 2-10 所示。图的具体内容和结构取决于你下载的图像。对于这个特定的例子，我们使用两组图像，每组分别是两个视角的白宫图像。

第 2 章　局部图像描述子 - 图22

图 2-10：使用局部描述子将在同一地理位置点拍摄图像进行分类

这个应用是使用局部描述子来匹配图像间区域的一个简单例子。在该应用中，我们没有使用针对任何匹配的限制约束。匹配的约束（具有很强的稳健性）可以通过接下来两章中的内容来实现。

练习

  • 为了让匹配具有更强的稳健性，修改用于匹配 Harris 角点的函数，使其输入参数中包含认为两点存在对应关系允许的最大像素距离。

  • 对一幅图像不断地应用模糊操作（或者 ROF 去噪），使得模糊效果越来越强，然后提取 Harris 角点，会出现什么问题？

  • 另一种 Harris 角点检测器是快速角点检测器。有很多快速角点检测器的实现方法，包括纯 Python 语言实现的版本，可以在 http://www.edwardrosten.com/work/fast.html 下载。尝试使用该检测器，使用敏感性的阈值，然后将结果和 Harris 角 点检测器检测出的角点比较。

  • 以不同分辨率创建一幅图像的副本（例如，可以尝试多次将图像的尺寸减半）。对每幅图像提取 SIFT 特征。绘制以及匹配特征，来发现尺度的独立性是如何以及何时失效的。

  • VLFeat 命令行工具同样实现了最大稳定极值区域（MSER，http://en.wikipedia.org/wiki/Maximally_stable_extremal_regions）算法。该算法是个能够找到角点一侧区域的区域检测器。创建一个用于提取 MSER 区域的函数，然后使用 -read-frames 选项将它们传递给 SIFT 特征描述子部分，最后写出一个用于绘制该区域边界的函数。

  • 基于对应关系，写出在图像对间匹配特征的函数，以实现估计尺度差异以及场景的平面旋转。

  • 任意选取一个位置，然后下载该位置的图像，像白宫例子一样将它们匹配起来。你能发现用于连接这些图像的更好方式吗？你是如何利用图来选取用于地理位置具有代表性的图像的？