第 3 章　图像到图像的映射

本章讲解图像之间的变换，以及一些计算变换的实用方法。这些变换可以用于图像扭曲变形和图像配准。最后，我们将会介绍一个自动创建全景图像的例子。

3.1　单应性变换

单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。在这里，平面是指图像或者三维中的平面表面。单应性变换具有很强的实用性，比如图像配准、图像纠正和纹理扭曲，以及创建全景图像。我们将频繁地使用单应性变换。本质上，单应性变换 H，按照下面的方程映射二维中的点（齐次坐标意义下）：

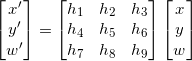\begin{bmatrix}x'\\y'\\ w'\end{bmatrix}=\begin{bmatrix}h_1 & h_2 & h_3\\h_4 & h_5 & h_6\\h_7 & h_8 & h_9\\\end{bmatrix}\begin{bmatrix}x\\y\\w\\\end{bmatrix} 或 x' = H x

对于图像平面内（甚至是三维中的点，后面我们会介绍到）的点，齐次坐标是个非常有用的表示方式。点的齐次坐标是依赖于其尺度定义的，所以，x=[x,y,w]=[αx,αy,αw]=[x/w,y/w,1] 都表示同一个二维点。因此，单应性矩阵 H 也仅依赖尺度定义，所以，单应性矩阵具有 8 个独立的自由度。我们通常使用 w=1 来归一化点，这样，点具有唯一的图像坐标 x 和 y。这个额外的坐标使得我们可以简单地使用一个矩阵来表示变换。

创建 homography.py 文件。下面的函数可以实现对点进行归一化和转换齐次坐标的功能，将其添加到 homography.py 文件中：

  1. def normalize(points):
  2.   """ 在齐次坐标意义下，对点集进行归一化，使最后一行为1 """
  3.     for row in points:
  4.       row /= points[-1]
  5.     return points
  7. def make_homog(points):
  8.   """ 将点集（dim×n 的数组）转换为齐次坐标表示 """
  10.   return vstack((points,ones((1,points.shape[1]))))

进行点和变换的处理时，我们会按照列优先的原则存储这些点。因此，n 个二维点集将会存储为齐次坐标意义下的一个 3×n 数组。这种格式使得矩阵乘法和点的变换操作更加容易。对于其他的例子，比如对于聚类和分类的特征，我们将使用典型的行数组来存储数据。

在这些投影变换中，有一些特别重要的变换。比如，仿射变换：

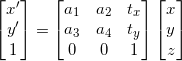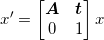
\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}a_1 & a_2 & t_x\\a_3 & a_4 & t_y\\0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix} 或 x'=\begin{bmatrix}\boldsymbol{A} & \boldsymbol{t}\\0 & 1\end{bmatrix}x

保持了 w=1, 不具有投影变换所具有的强大变形能力。仿射变换包含一个可逆矩阵 A 和一个平移向量 t=[tx,ty]。仿射变换可以用于很多应用，比如图像扭曲。

相似变换：

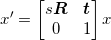
\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}s\cos(\theta) & -s \sin(\theta) & t_x\\s\sin(\theta) & -s \cos(\theta) & t_y\\0 & 0 & 1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} 或 x'=\begin{bmatrix}s\boldsymbol{R} & \boldsymbol{t}\\0 & 1\end{bmatrix}x

是一个包含尺度变化的二维刚体变换。上式中的向量 s 指定了变换的尺度，R 是角度为 θ 的旋转矩阵，t=[tx,ty] 在这里也是一个平移向量。如果 s=1，那么该变换能够保持距离不变。此时，变换为刚体变换。相似变换可以用于很多应用，比如图像配准。

下面让我们一起探讨如何设计用于估计单应性矩阵的算法，然后看一下使用仿射变换进行图像扭曲，使用相似变换进行图像匹配，以及使用完全投影变换进行创建全景图像的一些例子。

3.1.1　直接线性变换算法

单应性矩阵可以由两幅图像（或者平面）中对应点对计算出来。前面已经提到过，一个完全射影变换具有 8 个自由度。根据对应点约束，每个对应点对可以写出两个方程，分别对应于 x 和 y 坐标。因此，计算单应性矩阵 H 需要４个对应点对。

DLT（Direct Linear Transformation，直接线性变换）是给定 4 个或者更多对应点对矩阵，来计算单应性矩阵 H 的算法。将单应性矩阵 H 作用在对应点对上，重新写出该方程，我们可以得到下面的方程：

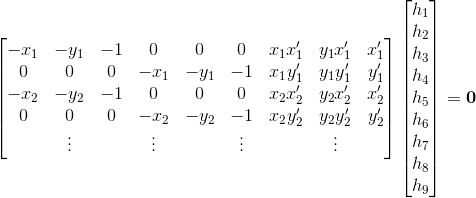
\begin{bmatrix}-x_1 & -y_1 & -1 & 0 & 0 & 0 & x_1 x'_1 & y_1x'_1 & x'_1\\0 & 0 & 0 & -x_1 & -y_1 & -1 & x_1y'_1 & y_1y'_1 & y'_1\\-x_2 & -y_2 & -1 & 0 & 0 & 0 & x_2x'_2 & y_2x'_2 & x'_2\\0 & 0 & 0 & -x_2 & -y_2 & -1 & x_2y'_2 & y_2y'_2 & y'_2\\ & \vdots & & \vdots & & \vdots & & \vdots\end{bmatrix}\begin{bmatrix}h_1\\h_2\\h_3\\h_4\\h_5\\h_6\\h_7\\h_8\\h_9\end{bmatrix}=\boldsymbol{0}

或者 Ah=0，其中 A 是一个具有对应点对二倍数量行数的矩阵。将这些对应点对方程的系数堆叠到一个矩阵中，我们可以使用 SVD（Singular Value Decomposition，奇异值分解）算法找到 H 的最小二乘解。下面是该算法的代码。将下面的函数添加到 homography.py 文件中：

  1. def H_from_points(fp,tp):
  2.   """ 使用线性DLT 方法，计算单应性矩阵H，使fp 映射到tp。点自动进行归一化"""
  4.   if fp.shape != tp.shape:
  5.     raise RuntimeError('number of points do not match')
  7.   # 对点进行归一化（对数值计算很重要）
  8.   # --- 映射起始点---
  9.   m = mean(fp[:2], axis=1)
  10.   maxstd = max(std(fp[:2], axis=1)) + 1e-9
  11.   C1 = diag([1/maxstd, 1/maxstd, 1])
  12.   C1[0][2] = -m[0]/maxstd
  13.   C1[1][2] = -m[1]/maxstd
  14.   fp = dot(C1,fp)
  16.   # --- 映射对应点---
  17.   m = mean(tp[:2], axis=1)
  18.   maxstd = max(std(tp[:2], axis=1)) + 1e-9
  19.   C2 = diag([1/maxstd, 1/maxstd, 1])
  20.   C2[0][2] = -m[0]/maxstd
  21.   C2[1][2] = -m[1]/maxstd
  22.   tp = dot(C2,tp)
  24.   # 创建用于线性方法的矩阵，对于每个对应对，在矩阵中会出现两行数值
  25.   nbr_correspondences = fp.shape[1]
  26.   A = zeros((2*nbr_correspondences,9))
  27.   for i in range(nbr_correspondences):
  28.      A[2*i] = [-fp[0][i],-fp[1][i],-1,0,0,0,
  29.            tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]]
  30.      A[2*i+1] = [0,0,0,-fp[0][i],-fp[1][i],-1,
  31.            tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]]
  33.   U,S,V = linalg.svd(A)
  34.   H = V[8].reshape((3,3))
  36.   # 反归一化
  37.   H = dot(linalg.inv(C2),dot(H,C1))
  39.   # 归一化，然后返回
  40.   return H / H[2,2]

上面函数的第一步操作是检查点对的两个数组中点的数目是否相同。如果不相同，函数将会抛出异常信息。这对于写出稳健的代码来说非常有用。但是，为了使得代码例子更简单、更容易理解，我们在本书中仅在很少的例子中使用异常处理技巧。你可以在 http://docs.python.org/library/exceptions.html 查阅更多关于异常类型的内容，以及在 http://docs.python.org/tutorial/errors.html 上了解如何使用它们。

对这些点进行归一化操作，使其均值为 0，方差为 1。因为算法的稳定性取决于坐标的表示情况和部分数值计算的问题，所以归一化操作非常重要。接下来我们使用 对应点对来构造矩阵 A。最小二乘解即为矩阵 SVD 分解后所得矩阵 V 的最后一行。 该行经过变形后得到矩阵 H。然后对这个矩阵进行处理和归一化，返回输出。

3.1.2　仿射变换

由于仿射变换具有 6 个自由度，因此我们需要三个对应点对来估计矩阵 H。通过将最后两个元素设置为 0，即 h7=h8=0，仿射变换可以用上面的 DLT 算法估计得出。

这里我们将使用不同的方法来计算单应性矩阵 H，这在文献 [13] 中有详细的描述（第 130 页）。下面的函数使用对应点对来计算仿射变换矩阵，将其添加到 homograph.py 文件中：

  1. def Haffine_from_points(fp,tp):
  2.   """ 计算H，仿射变换，使得tp 是fp 经过仿射变换H 得到的"""
  4.   if fp.shape != tp.shape:
  5.     raise RuntimeError('number of points do not match')
  7.   # 对点进行归一化
  8.   # --- 映射起始点---
  9.   m = mean(fp[:2], axis=1)
  10.   maxstd = max(std(fp[:2], axis=1)) + 1e-9
  11.   C1 = diag([1/maxstd, 1/maxstd, 1])
  12.   C1[0][2] = -m[0]/maxstd
  13.   C1[1][2] = -m[1]/maxstd
  14.   fp_cond = dot(C1,fp)
  16.   # --- 映射对应点---
  17.   m = mean(tp[:2], axis=1)
  18.   C2 = C1.copy() # 两个点集，必须都进行相同的缩放
  19.   C2[0][2] = -m[0]/maxstd
  20.   C2[1][2] = -m[1]/maxstd
  21.   tp_cond = dot(C2,tp)
  23.   # 因为归一化后点的均值为0，所以平移量为0
  24.   A = concatenate((fp_cond[:2],tp_cond[:2]), axis=0)
  25.   U,S,V = linalg.svd(A.T)
  27.   # 如Hartley 和Zisserman 著的Multiple View Geometry in Computer , Scond Edition 所示，
  28.   # 创建矩阵B 和C
  29.   tmp = V[:2].T
  30.   B = tmp[:2]
  31.   C = tmp[2:4]
  33.   tmp2 = concatenate((dot(C,linalg.pinv(B)),zeros((2,1))), axis=1)
  34.   H = vstack((tmp2,[0,0,1]))
  36.   # 反归一化
  37.   H = dot(linalg.inv(C2),dot(H,C1))
  39.   return H / H[2,2]

同样地，类似于 DLT 算法，这些点需要经过预处理和去处理化操作。在下一节中，让我们一起来看这些仿射变换是如何处理图像的。

3.2　图像扭曲

对图像块应用仿射变换，我们将其称为图像扭曲（或者仿射扭曲）。该操作不仅经常应用在计算机图形学中，而且经常出现在计算机视觉算法中。扭曲操作可以使用 SciPy 工具包中的 ndimage 包来简单完成。命令：

  1. transformed_im = ndimage.affine_transform(im,A,b,size)

使用如上所示的一个线性变换 A 和一个平移向量 b 来对图像块应用仿射变换。选项参数 size 可以用来指定输出图像的大小。默认输出图像设置为和原始图像同样大小。为了研究该函数是如何工作的，我们可以试着运行下面的命令：

  1. from scipy import ndimage
  3. im = array(Image.open('empire.jpg').convert('L'))
  4. H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
  5. im2 = ndimage.affine_transform(im,H[:2,:2],(H[0,2],H[1,2]))
  7. figure()
  8. gray()
  9. imshow(im2)
  10. show()

该命令输出结果图像如图 3-1（右）所示。可以看到，输出图像结果中丢失的像素用零来填充。

第 3 章　图像到图像的映射 - 图7

图 3-1：用仿射变换扭曲图像。原始图像（左图）以及使用 ndimage.affine_transform() 函数扭曲后的图像（右图）

3.2.1　图像中的图像

仿射扭曲的一个简单例子是，将图像或者图像的一部分放置在另一幅图像中，使得它们能够和指定的区域或者标记物对齐。

将函数 image_in_image() 添加到 warp.py 文件中。该函数的输入参数为两幅图像和一个坐标。该坐标为将第一幅图像放置到第二幅图像中的角点坐标：

  1. def image_in_image(im1,im2,tp):
  2.   """ 使用仿射变换将im1 放置在im2 上，使im1 图像的角和tp 尽可能的靠近
  3.     tp 是齐次表示的，并且是按照从左上角逆时针计算的"""
  5.   # 扭曲的点
  6.   m,n = im1.shape[:2]
  7.   fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
  9.   # 计算仿射变换，并且将其应用于图像im1
  10.   H = homography.Haffine_from_points(tp,fp)
  11.   im1_t = ndimage.affine_transform(im1,H[:2,:2],
  12.           (H[0,2],H[1,2]),im2.shape[:2])
  13.   alpha = (im1_t > 0)
  15.   return (1-alpha)*im2 + alpha*im1_t

正如你所看到的，该函数没有很多繁杂的操作。将扭曲的图像和第二幅图像融合，我们就创建了 alpha 图像。该图像定义了每个像素从各个图像中获取的像素值成分多少。这里我们基于以下事实，扭曲的图像是在扭曲区域边界之外以 0 来填充的图像，来创建一个二值的 alpha 图像。严格意义上说，我们需要在第一幅图像中的潜在 0 像素上加上一个小的数值，或者合理地处理这些 0 像素（参见本章结尾的练习部分）。注意，这里我们使用的图像坐标是齐次坐标意义下的。

试着使用该函数将公告牌中的一幅图像插入另一幅图像。下面几行代码会将图 3-2 中最左端的图像插入到第二幅图像中。这些坐标值是通过查看绘制的图像（在 PyLab 图像中，鼠标的坐标显示在图像底部附近）手工确定的。当然，也可以用 PyLab 类 库中的 ginput() 函数获得。

第 3 章　图像到图像的映射 - 图8

图 3-2：使用仿射变换将一幅图像放置到另一幅图像中

  1. import warp
  3. # 仿射扭曲im1 到im2 的例子
  4. im1 = array(Image.open('beatles.jpg').convert('L'))
  5. im2 = array(Image.open('billboard_for_rent.jpg').convert('L'))
  7. # 选定一些目标点
  8. tp = array([[264,538,540,264],[40,36,605,605],[1,1,1,1]])
  10. im3 = warp.image_in_image(im1,im2,tp)
  12. figure()
  13. gray()
  14. imshow(im3)
  15. axis('equal')
  16. axis('off')
  17. show()

上面的代码将图像放置在公告牌的上半部分。需要注意，标记物的坐标 tp 是用齐次坐标意义下的坐标表示的。将这些坐标换成：

  1. tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])

会将图像放置在公告牌的左下“for rent”部分。

函数 Haffine_from_points() 会返回给定对应点对的最优仿射变换。在上面的例子中，对应点对为图像和公告牌的角点。如果透视效应比较弱，那么这种方法会返回很好的结果。图 3-3 的上面一行显示出，在具有很强透视效应的情况下，在公告牌图像上使用射影变换输出图像的情况。在这种情况下，我们不可能使用同一个仿射变换将全部 4 个角点变换到它们的目标位置（尽管我们可以使用完全投影变换来完成该任务）。所以，当你打算使用仿射变换时，有一个很有用的技巧。

第 3 章　图像到图像的映射 - 图9

图 3-3：比较完全图像的仿射扭曲和使用两个三角形的仿射弯曲效果。图像放置在公告牌上，并且带有一些透视效应。对于整幅图像使用仿射扭曲效果不好。为了看清楚，我们将右边的两个角点放大（上）。使用包含两个三角形的仿射变换可以很好地将图像完全放置到公告牌上（下）

对于三个点，仿射变换可以将一幅图像进行扭曲，使这三对对应点对可以完美地匹配上。这是因为，仿射变换具有 6 个自由度，三个对应点对可以给出 6 个约束条件（对于这三个对应点对，x 和 y 坐标必须都要匹配）。所以，如果你真的打算使用仿射变换将图像放置到公告牌上，可以将图像分成两个三角形，然后对它们分别进行扭曲图像操作。下面是具体实现的代码：

  1. # 选定im1 角上的一些点
  2. m,n = im1.shape[:2]
  3. fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
  5. # 第一个三角形
  6. tp2 = tp[:,:3]
  7. fp2 = fp[:,:3]
  9. # 计算H
  10. H = homography.Haffine_from_points(tp2,fp2)
  11. im1_t = ndimage.affine_transform(im1,H[:2,:2],
  12.           (H[0,2],H[1,2]),im2.shape[:2])
  14. # 三角形的alpha
  15. alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
  16. im3 = (1-alpha)*im2 + alpha*im1_t
  18. # 第二个三角形
  19. tp2 = tp[:,[0,2,3]]
  20. fp2 = fp[:,[0,2,3]]
  22. # 计算H
  23. H = homography.Haffine_from_points(tp2,fp2)
  24. im1_t = ndimage.affine_transform(im1,H[:2,:2],
  25.           (H[0,2],H[1,2]),im2.shape[:2])
  27. # 三角形的alpha 图像
  28. alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
  29. im4 = (1-alpha)*im3 + alpha*im1_t
  31. figure()
  32. gray()
  33. imshow(im4)
  34. axis('equal')
  35. axis('off')
  36. show()

这里我们简单地为每个三角形创建了 alpha 图像，然后将所有的图像合并起来。该三角形的 alpha 图像可以简单地通过检查像素的坐标是否能够写成三角形顶点坐标的凸组合来计算得出 1。如果坐标可以表示成这种形式，那么该像素就位于三角形的内部。上面的例子使用了下面的函数 alpha_for_triangle()，将其添加到 warp.py 文件中。

1凸组合是形式为 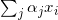\sum_j \alpha_jx_i 的线性组合（在三角形的例子中），其中所有的系数 αj非负，并且和为 1。

  1. def alpha_for_triangle(points,m,n):
  2.   """ 对于带有由points 定义角点的三角形，创建大小为(m，n) 的alpha 图
  3.     （在归一化的齐次坐标意义下）"""
  5.   alpha = zeros((m,n))
  6.     for i in range(min(points[0]),max(points[0])):
  7.       for j in range(min(points[1]),max(points[1])):
  8.         x = linalg.solve(points,[i,j,1])
  9.         if min(x) > 0: # 所有系数都大于零
  10.             alpha[i,j] = 1
  11.   return alpha

你的显卡可以极其快速地操作上面的代码。Python 语言的处理速度比你的显卡（或者 C/C++ 实现）慢很多，但是对于我们来说已经够用了。正如在图 3-3 下半部分所看到的，角点可以很好地匹配。

3.2.2　分段仿射扭曲

正如上面的例子所示，三角形图像块的仿射扭曲可以完成角点的精确匹配。让我们看一下对应点对集合之间最常用的扭曲方式：分段仿射扭曲。给定任意图像的标记点，通过将这些点进行三角剖分，然后使用仿射扭曲来扭曲每个三角形，我们可以将图像和另一幅图像的对应标记点扭曲对应。对于任何图形和图像处理库来说，这些都是最基本的操作。下面我们来演示一下如何使用 Matplotlib 和 SciPy 来完成该操作。

为了三角化这些点，我们经常使用狄洛克三角剖分方法。在 Matplotlib（但是不在 PyLab 库中）中有狄洛克三角剖分，我们可以用下面的方式使用它：

  1. import matplotlib.delaunay as md
  3. x,y = array(random.standard_normal((2,100)))
  4. centers,edges,tri,neighbors = md.delaunay(x,y)
  6. figure()
  7. for t in tri:
  8.     t_ext = [t[0], t[1], t[2], t[0]] # 将第一个点加入到最后
  9.     plot(x[t_ext],y[t_ext],'r')
  11. plot(x,y,'*')
  12. axis('off')
  13. show()

图 3-4 显示了一些实例点和三角剖分的结果。狄洛克三角剖分选择一些三角形，使三角剖分中所有三角形的最小角度最大 2。函数 delaunay() 有 4 个输出，其中我们仅需要三角形列表信息（第三个输出）。在 warp.py 文件中创建用于三角剖分的函数：

2三角剖分中的边实际上是泰森图的对偶图。参见 http://en.wikipedia.org/wiki/Delaunay_triangulation。

  1. import matplotlib.delaunay as md
  3. def triangulate_points(x,y):
  4.   """ 二维点的Delaunay 三角剖分"""
  6.   centers,edges,tri,neighbors = md.delaunay(x,y)
  7.   return tri

函数输出的是一个数组，该数组的每一行包含对应数组 x 和 y 中每个三角形三个点的切片。

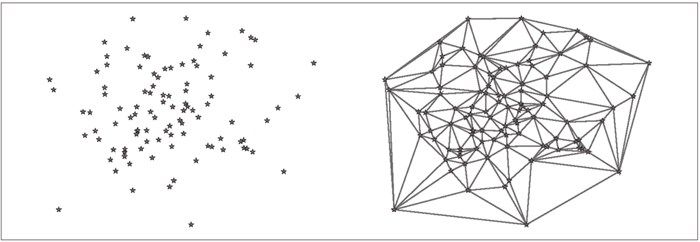
第 3 章　图像到图像的映射 - 图11

图 3-4：随机二维点集的狄洛克三角剖分示例

现在让我们将该算法应用于一个例子，在该例子中，在 5×6 的网格上使用 30 个控制点，将一幅图像扭曲到另一幅图像中的非平坦区域。图 3-5b 所示的是将一幅图像扭曲到“turning torso”的表面。目标点是使用 ginput() 函数手工选取出来的，将结果保存在 turningtorso_points.txt 文件中。

首先，我们需要写出一个用于分段仿射图像扭曲的通用扭曲函数。下面的代码可以实现该功能。在该代码中，我们也展示了如何扭曲一幅彩色图像（你仅需要对每个颜色通道进行扭曲）。

  1. def pw_affine(fromim,toim,fp,tp,tri):
  2.   """ 从一幅图像中扭曲矩形图像块
  3.     fromim= 将要扭曲的图像
  4.     toim= 目标图像
  5.     fp= 齐次坐标表示下，扭曲前的点
  6.     tp= 齐次坐标表示下，扭曲后的点
  7.     tri= 三角剖分"""
  9.   im = toim.copy()
  11.   # 检查图像是灰度图像还是彩色图象
  12.   is_color = len(fromim.shape) == 3
  14.   # 创建扭曲后的图像（如果需要对彩色图像的每个颜色通道进行迭代操作，那么有必要这样做）
  15.   im_t = zeros(im.shape, 'uint8')
  17.   for t in tri:
  18.     # 计算仿射变换
  19.     H = homography.Haffine_from_points(tp[:,t],fp[:,t])
  21.     if is_color:
  22.       for col in range(fromim.shape[2]):
  23.       im_t[:,:,col] = ndimage.affine_transform(
  24.         fromim[:,:,col],H[:2,:2],(H[0,2],H[1,2]),im.shape[:2])
  25.     else:
  26.       im_t = ndimage.affine_transform(
  27.         fromim,H[:2,:2],(H[0,2],H[1,2]),im.shape[:2])
  29.     # 三角形的alpha
  30.     alpha = alpha_for_triangle(tp[:,t],im.shape[0],im.shape[1])
  32.     # 将三角形加入到图像中
  33.     im[alpha>0] = im_t[alpha>0]
  35.   return im

在该代码中，我们首先检查该图像是灰度图像还是彩色图像。如果图像为彩色图像，则对每个颜色通道进行扭曲处理。因为对于每个三角形来说，仿射变换是唯一确定的，所以我们这里使用 Haffine_from_points() 函数来处理。将上面的函数添加到 warp.py 文件中。

为了将该函数应用到当前例子中，接下来的简短脚本将这些操作统一起来：

  1. import homography
  2. import warp
  4. # 打开图像，并将其扭曲
  5. fromim = array(Image.open('sunset_tree.jpg'))
  6. x,y = meshgrid(range(5),range(6))
  7. x = (fromim.shape[1]/4) * x.flatten()
  8. y = (fromim.shape[0]/5) * y.flatten()
  10. # 三角剖分
  11. tri = warp.triangulate_points(x,y)
  13. # 打开图像和目标点
  14. im = array(Image.open('turningtorso1.jpg'))
  15. tp = loadtxt('turningtorso1_points.txt') # destination points
  17. # 将点转换成齐次坐标
  18. fp = vstack((y,x,ones((1,len(x)))))
  19. tp = vstack((tp[:,1],tp[:,0],ones((1,len(tp)))))
  21. # 扭曲三角形
  22. im = warp.pw_affine(fromim,im,fp,tp,tri)
  24. # 绘制图像
  25. figure()
  26. imshow(im)
  27. warp.plot_mesh(tp[1],tp[0],tri)
  28. axis('off')
  29. show()

输出结果如图 3-5c 所示。我们通过下面的辅助函数（将其添加到 warp.py 文件中）来绘制出图像中的这些三角形：

  1. def plot_mesh(x,y,tri):
  2.   """ 绘制三角形"""
  4.   for t in tri:
  5.     t_ext = [t[0], t[1], t[2], t[0]] # 将第一个点加入到最后
  6.     plot(x[t_ext],y[t_ext],'r')

第 3 章　图像到图像的映射 - 图12

图 3-5：使用狄洛克三角剖分标记点进行分段仿射扭曲：（a）为带有标记物的目标图像；（b）为带有三角剖分的图像；（c）为扭曲后的图像；（d）为带有三角剖分的扭曲图像

这个例子应该能够帮助你在应用中做图像的分段仿射扭曲。我们可以对该例子中的函数进行改进。我们将其中一部分留作练习，剩下的留给你自己解决。

3.2.3　图像配准

图像配准是对图像进行变换，使变换后的图像能够在常见的坐标系中对齐。配准可以是严格配准，也可以是非严格配准。为了能够进行图像对比和更精细的图像分析，图像配准是一步非常重要的操作。

让我们一起看一个对多个人脸图像进行严格配准的例子。该配准使得我们计算的平均人脸和人脸表观的变化具有意义。因为，图像中的人脸并不都有相同的大小、位置和方向，所以，在这种类型的配准中，我们实际上是寻找一个相似变换（带有尺度变化的刚体变换），在对应点对之间建立映射。

在 jkface.zip 文件中有 366 幅单人图像（2008 年，每天一幅）。3 这些图像都对眼睛和嘴的坐标进行了标记，结果保存在 jkface.xml 文件中。使用这些点，我们可以计算出一个相似变换，然后将可以使用该变换（包含尺度变换）的这些图像扭曲到一个归一化的坐标系中。为了读取 XML 格式的文件，我们将会使用 Python 中内置 xml.dom 模块中的 minidom 类库。

3这些图像是由 J. K. Keller（经过许可）提供的，详情参见 http://jk-keller.com/daily-photo/。

该 XML 文件看起来类似于下面的格式：

  1. <?xml version="1.0" encoding="utf-8"?>
  2. <faces>
  3.          <face file="jk-002.jpg" xf="46" xm="56" xs="67" yf="38" ym="65" ys="39">
  4.          <face file="jk-006.jpg" xf="38" xm="48" xs="59" yf="38" ym="65" ys="38">
  5.          <face file="jk-004.jpg" xf="40" xm="50" xs="61" yf="38" ym="66" ys="39">
  6.          <face file="jk-010.jpg" xf="33" xm="44" xs="55" yf="38" ym="65" ys="38">
  7. …
  8. </faces>

为了从该文件中读取这些坐标，我们需要将使用 minidom 的函数添加到新文件 imregistration.py 中：

  1. from xml.dom import minidom
  3. def read_points_from_xml(xmlFileName):
  4.   """ 读取用于人脸对齐的控制点"""
  6.   xmldoc = minidom.parse(xmlFileName)
  7.   facelist = xmldoc.getElementsByTagName('face')
  8.   faces = {}
  9.   for xmlFace in facelist:
  10.     fileName = xmlFace.attributes['file'].value
  11.     xf = int(xmlFace.attributes['xf'].value)
  12.     yf = int(xmlFace.attributes['yf'].value)
  13.     xs = int(xmlFace.attributes['xs'].value)
  14.     ys = int(xmlFace.attributes['ys'].value)
  15.     xm = int(xmlFace.attributes['xm'].value)
  16.     ym = int(xmlFace.attributes['ym'].value)
  17.     faces[fileName] = array([xf, yf, xs, ys, xm, ym])
  18.   return faces

这些标记点会在 Python 中以字典的形式返回，字典的键值为图像的文件名。格式为：图像中左眼（人脸右侧）的坐标为 xf 和 yf，右眼的坐标为 xs 和 ys，嘴的坐标 为 xm 和 ym。为了计算相似变换中的参数，我们可以使用最小二乘解来解决。对于每个点 xi=[xi, yi]（在这个例子中，每幅图像有三个点），这些点应该被映射到目标位置 [\hat x_i,\hat y_i]，如下所示：

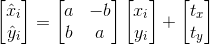
\begin{bmatrix}\hat x_i\\\hat y_i\end{bmatrix}=\begin{bmatrix}a & -b\\b & a\end{bmatrix}\begin{bmatrix}x_i\\y_i\end{bmatrix}+\begin{bmatrix}t_x\\t_y\end{bmatrix}

将这三个点都表示成该形式，我们可以重新将其写成方程组的形式。该方程组中含有 a、b、tx、ty未知量，如下所示：

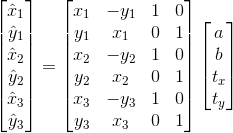
\begin{bmatrix}\hat x_1\\\hat y_1\\\hat x_2\\\hat y_2\\\hat x_3\\\hat y_3\\\end{bmatrix}=\begin{bmatrix}x_1 & -y_1 & 1 & 0\\y_1 & x_1 & 0 & 1\\x_2 & -y_2 & 1 & 0\\y_2 & x_2 & 0 & 1\\x_3 & -y_3 & 1 & 0\\y_3 & x_3 & 0 & 1\end{bmatrix}\begin{bmatrix}a\\b\\t_x\\t_y\end{bmatrix}

下面我们使用相似矩阵的参数化表示方式：

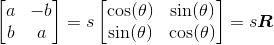
\begin{bmatrix}a & -b\\b & a\end{bmatrix}=s\begin{bmatrix}\cos(\theta) & \sin(\theta)\\\sin(\theta) & \cos(\theta)\end{bmatrix}=s\boldsymbol{R}

其中尺度 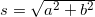s=\sqrt{a^2+b^2}，旋转矩阵为 R。

如果存在更多的对应点对，其计算公式相同，只需在矩阵中额外添加几行。你可以使用 linalg.lstsq() 函数来计算该问题的最小二乘解。使用最小二乘解的思想是一个标准技巧，我们还会在本书中多次使用。实际上，这和之前在 DLT 算法中使用的方式相同。

函数的具体代码如下（将其添加到 imregistration.py 文件中）：

  1. from scipy import linalg
  3. def compute_rigid_transform(refpoints,points):
  4.   """ 计算用于将点对齐到参考点的旋转、尺度和平移量"""
  6.   A = array([ [points[0], -points[1], 1, 0],
  7.               [points[1], points[0], 0, 1],
  8.               [points[2], -points[3], 1, 0],
  9.               [points[3], points[2], 0, 1],
  10.               [points[4], -points[5], 1, 0],
  11.               [points[5], points[4], 0, 1]])
  13.   y = array([ refpoints[0],
  14.               refpoints[1],
  15.               refpoints[2],
  16.               refpoints[3],
  17.               refpoints[4],
  18.               refpoints[5]])
  20.   # 计算最小化||Ax -y || 的最小二乘解
  21.   a,b,tx,ty = linalg.lstsq(A,y)[0]
  22.   R = array([[a, -b], [b, a]]) # 包含尺度的旋转矩阵
  24.   return R,tx,ty

该函数返回一个具有尺度的旋转矩阵，以及在 x 和 y 方向上的平移量。为了扭曲图像，并保存对齐后的新图像，我们可以对每个颜色通道（这些图像都是彩色图像）应用 ndimage.affine_transform() 函数操作。作为参考坐标系，你可以使用任何三个点的坐标。这里我们为了简单起见，直接使用第一幅图像中的标记位置：

  1. from scipy import ndimage
  2. from scipy.misc import imsave
  3. import os
  5. def rigid_alignment(faces,path,plotflag=False):
  6.   """ 严格对齐图像，并将其保存为新的图像
  7.     path 决定对齐后图像保存的位置
  8.     设置plotflag=True，以绘制图像"""
  10.   # 将第一幅图像中的点作为参考点
  11.   refpoints = faces.values()[0]
  13.   # 使用仿射变换扭曲每幅图像
  14.   for face in faces:
  15.     points = faces[face]
  16.   R,tx,ty = compute_rigid_transform(refpoints, points)
  17.   T = array([[R[1][1], R[1][0]], [R[0][1], R[0][0]]])
  19.   im = array(Image.open(os.path.join(path,face)))
  20.   im2 = zeros(im.shape, 'uint8')
  22.   # 对每个颜色通道进行扭曲
  23.   for i in range(len(im.shape)):
  24.     im2[:,:,i] = ndimage.affine_transform(im[:,:,i],linalg.inv(T),offset=[-ty,-tx])
  26.   if plotflag:
  27.     imshow(im2)
  28.     show()
  30.   # 裁剪边界，并保存对齐后的图像
  31.   h,w = im2.shape[:2]
  32.   border = (w+h)/20
  34.   # 裁剪边界
  35.   imsave(os.path.join(path, 'aligned/'+face),im2[border:h-border,border:w-border,:])

这里我们使用 imsave() 函数来将对齐后的图像保存到 aligned 子文件夹中。

接下来的简短脚本会读取 XML 文件，其中文件名为键，点的坐标为键值。然后配准所有的图像，将它们与第一幅图像对齐：

  1. import imregistration
  3. # 载入控制点的位置
  4. xmlFileName = 'jkfaces2008_small/jkfaces.xml'
  5. points = imregistration.read_points_from_xml(xmlFileName)
  7. # 注册
  8. imregistration.rigid_alignment(points,'jkfaces2008_small/')

运行这些代码，你能够在子目录中得到这些对齐后的人脸图像。图 3-6 所示为配准前后的 6 幅样本图像。由于配准后图像的边界可能会出现不想要的黑色填充像素，所以我们对配准后的图像进行轻微的修剪，来删除这些黑色填充像素。

第 3 章　图像到图像的映射 - 图18

图 3-6：配准之前（上）和配准之后（下）的样本图像

现在让我们看配准操作如何影响平均图像。图 3-7 为未对齐人脸图像的平均图像，旁边是对齐后图像的平均图像。（注意，由于对齐后图像的边界有裁剪，所以两幅图像的大小有差异）尽管在原始图像中，人脸的尺寸、方向和位置变化都很小，但是配准操作对平均图像的计算结果影响很大。

第 3 章　图像到图像的映射 - 图19

图 3-7：平均图像的比较：没有对齐操作（左）；经过三点刚体对齐操作（右）

自然地，使用未准确配准的图像同样对主成分的计算结果有着很大的影响。图 3-8 表示，从未经过配准和经过配准的数据集中选取前 150 幅图像，PCA 的计算结果。正如平均图像一样，未配准的 PCA 模式是模糊的。在计算主成分时，我们使用以平均人脸位置为中心的椭圆掩膜。在堆叠这些图像之前，将这些图像和掩膜相乘，我们能够避免将背景变化带入到 PCA 模式中。将 1.3 节 PCA 例子中创建矩阵的一行替换为：

  1. immatrix = array([mask*array(Image.open(imlist[i]).convert('L')).flatten()
  2.            for i in range(150)],'f')

其中 mask 是一副同样大小的二值图像，已经经过压平处理。

第 3 章　图像到图像的映射 - 图20

图 3-8：比较未配准和已配准图像的 PCA 模式：未经过配准的平均图像和前 9 个主成分（上）；经过配准后的平均图像和前 9 个主成分（下）

3.3　创建全景图

在同一位置（即图像的照相机位置相同）拍摄的两幅或者多幅图像是单应性相关的（如图 3-9 所示）。我们经常使用该约束将很多图像缝补起来，拼成一个大的图像来创建全景图像。在本节中，我们将探讨如何创建全景图像。

第 3 章　图像到图像的映射 - 图21

图 3-9：瑞典隆德主要大学建筑的５幅图像。这些图像都是从同一个视点拍摄的

3.3.1　RANSAC

RANSAC 是“RANdom SAmple Consensus”（随机一致性采样）的缩写。该方法是用来找到正确模型来拟合带有噪声数据的迭代方法。给定一个模型，例如点集之间的单应性矩阵，RANSAC 基本的思想是，数据中包含正确的点和噪声点，合理的模型应该能够在描述正确数据点的同时摒弃噪声点。

RANSAC 的标准例子：用一条直线拟合带有噪声数据的点集。简单的最小二乘在该例子中可能会失效，但是 RANSAC 能够挑选出正确的点，然后获取能够正确拟合的直线。下面来看使用 RANSAC 的例子。你可以从 http://www.scipy.org/Cookbook/RANSAC 下载 ransac.py，里面包含了特定的例子作为测试用例。图 3-10 为运行 ransac.text() 的例子。可以看到，该算法只选择了和直线模型一致的数据点，成功 地找到了正确的解。

RANSAC 是个非常有用的算法，我们将在下一节估计单应性矩阵和其他一些例子中使用它。关于 RANSAC 更多的信息，参见 Fischler 和 Bolles 的原始论文 [11]、维基百科 http://en.wikipedia.org/wiki/RANSAC 或者技术报告 [40]。

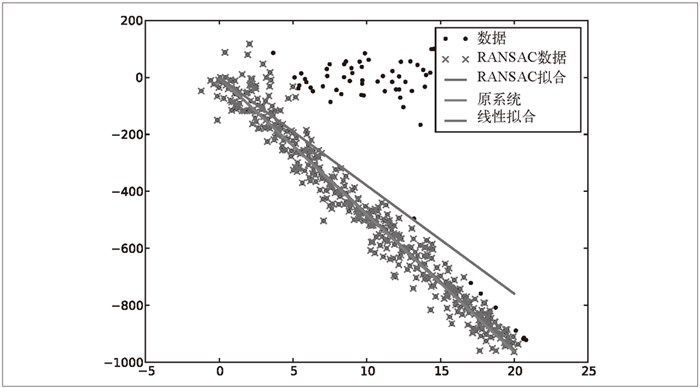
第 3 章　图像到图像的映射 - 图22

图 3-10：使用 RANSAC 算法用一条直线来拟合包含噪声数据点集

3.3.2　稳健的单应性矩阵估计

我们在任何模型中都可以使用 RANSAC 模块。在使用 RANSAC 模块时，我们只需要在相应 Python 类中实现 fit() 和 get_error() 方法，剩下就是正确地使用 ransac.py。我们这里使用可能的对应点集来自动找到用于全景图像的单应性矩阵。图 3-11 所示为使用 SIFT 特征自动找到匹配对应。这可以通过运行下面的命令来实现：

  1. import sift
  3. featname = ['Univ'+str(i+1)+'.sift' for i in range(5)]
  4. imname = ['Univ'+str(i+1)+'.jpg' for i in range(5)]
  5. l = {}
  6. d = {}
  7. for i in range(5):
  8.   sift.process_image(imname[i],featname[i])
  9.   l[i],d[i] = sift.read_features_from_file(featname[i])
  11. matches = {}
  12. for i in range(4):
  13.   matches[i] = sift.match(d[i+1],d[i])

显然，并不是所有图像中的对应点对都是正确的。实际上，SIFT 是具有很强稳健性的描述子，能够比其他描述子，例如图像块相关的 Harris 角点，产生更少的错误的匹配。但是该方法仍然远非完美。

第 3 章　图像到图像的映射 - 图23

图 3-11：在连续图像对间使用 SIFT 特征寻找匹配对应点对

我们使用 RANSAC 算法来求解单应性矩阵，首先需要将下面模型类添加到 homography.py 文件中：

  1. class RansacModel(object):
  2.   """ 用于测试单应性矩阵的类，其中单应性矩阵是由网站http://www.scipy.org/Cookbook/RANSAC 上的ransac.py 计算出来的"""
  4.   def __init__(self,debug=False):
  5.     self.debug = debug
  7.   def fit(self, data):
  8.   """ 计算选取的4 个对应的单应性矩阵 """
  10.   # 将其转置，来调用H_from_points() 计算单应性矩阵
  11.   data = data.T
  13.   # 映射的起始点
  14.   fp = data[:3,:4]
  15.   # 映射的目标点
  16.   tp = data[3:,:4]
  18.   # 计算单应性矩阵，然后返回
  19.   return H_from_points(fp,tp)
  21. def get_error( self, data, H):
  22.   """ 对所有的对应计算单应性矩阵，然后对每个变换后的点，返回相应的误差"""
  24.   data = data.T
  26.   # 映射的起始点
  27.   fp = data[:3]
  28.   # 映射的目标点
  29.   tp = data[3:]
  31.   # 变换fp
  32.   fp_transformed = dot(H,fp)
  34.   # 归一化齐次坐标
  35.   for i in range(3):
  36.     fp_transformed[i] /= fp_transformed[2]
  38.   # 返回每个点的误差
  39.   return sqrt( sum((tp-fp_transformed)**2,axis=0) )

可以看到，这个类包含 fit() 方法。该方法仅仅接受由 ransac.py 选择的４个对应点对（data 中的前 4 个点对），然后拟合一个单应性矩阵。记住，4 个点对是计算单应性矩阵所需的最少数目。由于 get_error() 方法对每个对应点对使用该单应性矩阵，然后返回相应的平方距离之和，因此 RANSAC 算法能够判定哪些点对是正确的，哪些是错误的。在实际中，我们需要在距离上使用一个阈值来决定哪些单应性矩阵是合理的。为了方便使用，将下面的函数添加到 homography.py 文件中：

  1. def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):
  2.   """ 使用RANSAC 稳健性估计点对应间的单应性矩阵H（ransac.py 为从 http://www.scipy.org/Cookbook/RANSAC 下载的版本）
  4.     # 输入：齐次坐标表示的点fp，tp（3×n 的数组）"""
  6.   import ransac
  8.   # 对应点组
  9.   data = vstack((fp,tp))
  11.   # 计算H，并返回
  12.   H,ransac_data = ransac.ransac(data.T,model,4,maxiter,match_theshold,10, return_all=True)
  13.   return H,ransac_data['inliers']

该函数同样允许提供阈值和最小期望的点对数目。最重要的参数是最大迭代次数：程序退出太早可能得到一个坏解；迭代次数太多会占用太多时间。函数的返回结果为单应性矩阵和对应该单应性矩阵的正确点对。

类似于下面的操作，你可以将 RANSAC 算法应用于对应点对上：

  1. # 将匹配转换成齐次坐标点的函数
  2. def convert_points(j):
  3.   ndx = matches[j].nonzero()[0]
  4.   fp = homography.make_homog(l[j+1][ndx,:2].T)
  5.   ndx2 = [int(matches[j][i]) for i in ndx]
  6.   tp = homography.make_homog(l[j][ndx2,:2].T)
  7.   return fp,tp
  9. # 估计单应性矩阵
  10. model = homography.RansacModel()
  12. fp,tp = convert_points(1)
  13. H_12 = homography.H_from_ransac(fp,tp,model)[0] # im1 到im2 的单应性矩阵
  15. fp,tp = convert_points(0)
  16. H_01 = homography.H_from_ransac(fp,tp,model)[0] # im0 到im1 的单应性矩阵
  18. tp,fp = convert_points(2) # 注意：点是反序的
  19. H_32 = homography.H_from_ransac(fp,tp,model)[0] # im3 到im2 的单应性矩阵
  21. tp,fp = convert_points(3) # 注意：点是反序的
  22. H_43 = homography.H_from_ransac(fp,tp,model)[0] # im4 到im3 的单应性矩阵

在该例子中，图像 2 是中心图像，也是我们希望将其他图像变成的图像。图像 0 和图像 1 应该从右边扭曲，图像 3 和图像 4 从左边扭曲。在每个图像对中，由于匹配是从最右边的图像计算出来的，所以我们将对应的顺序进行了颠倒，使其从左边图像开始扭曲。因为我们不关心该扭曲例子中的正确点对，所以仅需要该函数的第一个输出（单应性矩阵）。

3.3.3　拼接图像

估计出图像间的单应性矩阵（使用 RANSAC 算法），现在我们需要将所有的图像扭曲到一个公共的图像平面上。通常，这里的公共平面为中心图像平面（否则，需要进行大量变形）。一种方法是创建一个很大的图像，比如图像中全部填充 0，使其和中心图像平行，然后将所有的图像扭曲到上面。由于我们所有的图像是由照相机水平旋转拍摄的，因此我们可以使用一个较简单的步骤：将中心图像左边或者右边的区域填充 0，以便为扭曲的图像腾出空间。将下面的代码添加到 warp.py 文件中：

  1. def panorama(H,fromim,toim,padding=2400,delta=2400):
  2.   """ 使用单应性矩阵H（使用RANSAC 健壮性估计得出），协调两幅图像，创建水平全景图像。结果
  3.     为一幅和toim 具有相同高度的图像。padding 指定填充像素的数目，delta 指定额外的平移量"""
  5.   # 检查图像是灰度图像，还是彩色图像
  6.   is_color = len(fromim.shape) == 3
  8.   # 用于geometric_transform() 的单应性变换
  9.   def transf(p):
  10.     p2 = dot(H,[p[0],p[1],1])
  11.     return (p2[0]/p2[2],p2[1]/p2[2])
  13.   if H[1,2]<0: # fromim 在右边
  14.     print 'warp - right'
  15.     # 变换fromim
  16.     if is_color:
  17.       # 在目标图像的右边填充0
  18.       toim_t = hstack((toim,zeros((toim.shape[0],padding,3))))
  19.       fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
  20.       for col in range(3):
  21.         fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
  22.                     transf,(toim.shape[0],toim.shape[1]+padding))
  23.   else:
  24.     # 在目标图像的右边填充0
  25.     toim_t = hstack((toim,zeros((toim.shape[0],padding))))
  26.     fromim_t = ndimage.geometric_transform(fromim,transf,
  27.                   (toim.shape[0],toim.shape[1]+padding))
  28.   else:
  29.     print 'warp - left'
  30.     # 为了补偿填充效果，在左边加入平移量
  31.     H_delta = array([[1,0,0],[0,1,-delta],[0,0,1]])
  32.     H = dot(H,H_delta)
  33.     # fromim 变换
  34.     if is_color:
  35.     # 在目标图像的左边填充0
  36.     toim_t = hstack((zeros((toim.shape[0],padding,3)),toim))
  37.     fromim_t = zeros((toim.shape[0],toim.shape[1]+padding,toim.shape[2]))
  38.     for col in range(3):
  39.       fromim_t[:,:,col] = ndimage.geometric_transform(fromim[:,:,col],
  40.                   transf,(toim.shape[0],toim.shape[1]+padding))
  41.   else:
  42.   # 在目标图像的左边填充0
  43.   toim_t = hstack((zeros((toim.shape[0],padding)),toim))
  44.   fromim_t = ndimage.geometric_transform(fromim,
  45.                 transf,(toim.shape[0],toim.shape[1]+padding))
  47.   # 协调后返回（将fromim 放置在toim 上）
  48.   if is_color:
  49.     # 所有非黑色像素
  50.     alpha = ((fromim_t[:,:,0]  fromim_t[:,:,1]  fromim_t[:,:,2] ) > 0)
  51.     for col in range(3):
  52.       toim_t[:,:,col] = fromim_t[:,:,col]*alpha + toim_t[:,:,col]*(1-alpha)
  53.   else:
  54.     alpha = (fromim_t > 0)
  55.     toim_t = fromim_t*alpha + toim_t*(1-alpha)
  57.   return toim_t

对于通用的 geometric_transform() 函数，我们需要指定能够描述像素到像素间映射的函数。在这个例子中，transf() 函数就是该指定的函数。该函数通过将像素和 H 相乘，然后对齐次坐标进行归一化来实现像素间的映射。通过查看 H 中的平移量， 我们可以决定应该将该图像填补到左边还是右边。当该图像填补到左边时，由于目标图像中点的坐标也变化了，所以在“左边”情况中，需要在单应性矩阵中加入平移。简单起见，我们同样使用 0 像素的技巧来寻找 alpha 图。

现在在图像中使用该操作，函数如下所示：

  1. # 扭曲图像
  2. delta = 2000 # 用于填充和平移
  4. im1 = array(Image.open(imname[1]))
  5. im2 = array(Image.open(imname[2]))
  6. im_12 = warp.panorama(H_12,im1,im2,delta,delta)
  8. im1 = array(Image.open(imname[0]))
  9. im_02 = warp.panorama(dot(H_12,H_01),im1,im_12,delta,delta)
  11. im1 = array(Image.open(imname[3]))
  12. im_32 = warp.panorama(H_32,im1,im_02,delta,delta)
  14. im1 = array(Image.open(imname[j+1]))
  15. im_42 = warp.panorama(dot(H_32,H_43),im1,im_32,delta,2*delta)

注意，在最后一行中，im_32 图像已经发生了一次平移。创建的全景图结果如图 3-12 所示。正如你所看到的，图像曝光不同，在单个图像的边界上存在边缘效应。商业的创建全景图像软件里有额外的操作来对强度进行归一化，并对平移进行平滑场景转换，以使得结果看上去更好。

第 3 章　图像到图像的映射 - 图24

图 3-12：使用 SIFT 对应点对自动创建水平全景图像：全部的全景图像（上）；对中心部分图像进行裁剪后的图像（下）

练习

  • 写出一个函数，其输入参数为正方形（或者长方形）物体（例如，一本书、一张海报，或者二维条形码）图像的坐标。然后，计算将该长方形映射归一化坐标系中正视图全图的变换。你可以使用 ginput()，或者最强的 Harris 角点来发现长方形物体的稳健性角点。

  • 写出一个函数，对于如图 3-1 所示的扭曲能够正确地找到 alpha 图像。

  • 在你自己的数据集中找出包含三个公共的标记物（像人脸例子一样，或者使用著名的景物，比如埃菲尔铁塔）的那个。创建对齐后的图像，其中这些标记物在同一个位置上。计算平均和中值图像，然后可视化。

  • 进行亮度归一化操作，找出在全景图像例子中更好地拼接图像的方法。该方法能够去除图 3-12 中的边缘效应。

  • 与将图像扭曲到中心图像上不同，全景图像可以通过将图像扭曲到圆柱体上来创建。试着在图 3-12 的例子中使用该方式创建全景图像。

  • 使用 RANSAC 算法来找到一些主要的正确单应性矩阵集合。一个简单的方式是，首先运行一次 RANSAC 算法，找到具有最大一致子集的单应性矩阵，然后将与该单应性矩阵一致的对应点对从匹配集合中删除，再运行 RANSAC 算法找到下一个最大的集合，以此类推。

  • 修改单应性矩阵的 RANSAC 估计算法，来使用三个对应点对计算仿射变换。使用该算法来判断图像对之间是否包含平面场景，例如使用正确点的个数。对于仿射变化，平面场景中正确点的个数会很多。

  • 通过匹配局部特征，以及使用最小二乘刚体配准，用多个图像（例如，从 Flickr 下载）创建一个全景图（http://en.wikipedia.org/wiki/Panography）。