第 1 章 科学计算概况与选择Python的理由
科学计算(scientific computing)是指在科学与工程领域,使用计算机数学建模和数值分析技术分析和解决问题的过程。科学问题包括不同科学学科中的问题,如地球科学、空间科学、社会科学、生命科学、物理学和形式科学。这些学科基本涵盖了现有的所有科学领域,从传统科学到现代工程科学,如计算机科学,都在其中。工程问题包括从土木工程和电子工程到(最新的)生物医学工程领域的各种问题。
本章将介绍的话题如下:
科学计算的基础知识
科学计算的处理流程
科学与工程领域的计算案例
解决复杂问题的策略
近似、误差和相关统计术语
误差分析的基本概念
计算机算法与浮点数
Python背景介绍
为什么选择Python做科学计算
数学建模是指利用数学术语表示设备、物体、现象和观念的行为的建模行为。一般情况下,数学建模可以帮助人们更好地理解观念、设备和物体的行为或观测值。它可以帮助人们解释观测值,并对未来的行为进行预测,或者推导出还没有被观测或测量的结果。数值分析是计算机科学与数学的交叉领域,通过设计、分析并最终实现算法,来解决自然科学(例如物理学、生物学和地球科学)、社会科学(例如经济学、心理学、社会学和政治学)、工程学、医学和商学问题。Python有一个专门研究多体动力学的包和工作流,叫作Python Dynamics(即PyDy)。它是基于SymPy力学包开发的工作流和软件包。PyDy扩展了SymPy,并实现了多体动力学仿真。
1.1 科学计算的定义
科学计算也被称作计算科学(computational science)或科学计算法(scientific computation),其主要思路是开发数学模型,通过量化分析技术和计算机解决科学问题。
“科学计算是利用计算机解决科学与工程领域的数学建模问题所需的工具、技术和理论的集合。”
——Gene H. Golub和James M. Ortega
简而言之,科学计算可以看成是一门交叉学科,如下图所示。
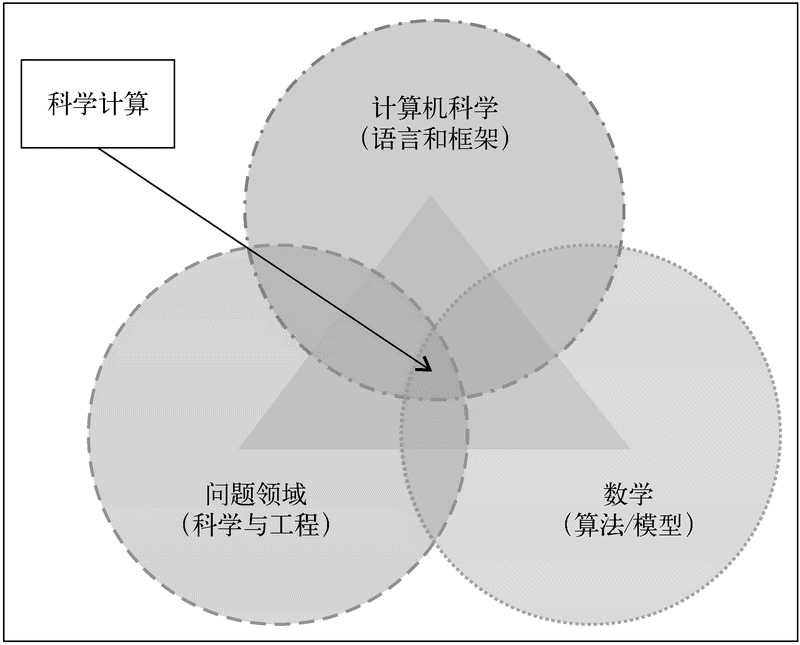
科学计算是一门交叉学科
科学计算首先需要人们了解问题(通常是科学和工程领域的问题)背后的专业知识,同时需要具有数学建模能力,掌握各种数值分析技术,并能利用计算机技术实现高效率、高性能的计算工具。它还需要使用计算机以及各种各样的外围设备,包括网络设备、存储工具、计算处理器、数学与数值分析软件。此外还需要掌握编程语言,并了解问题所在领域的知识数据库。人们已经利用科学计算的相关技术创造出了新的应用,让科学家们能够从现有的数据和过程中发现新的知识。
在计算机科学方面,科学计算可以看成是对数学模型和问题所在领域的数据/信息的数值仿真。仿真目标由具体问题决定。目标可以是探索事件发生的原因,重新构建一个具体的场景,优化过程,或者预测事件发生的时机。有时数值仿真可能是唯一选择,或者是最佳选择。有一些现象和场景基本上不可能进行实验,例如气候研究、天体物理学研究和天气预测。在另一些场景中,实际的实验并不可取,比如检验某种材料或产品的可靠性或强度。有些实验的时间/经济成本很高,例如车祸或生命科学实验。在以上这些场景中,科学计算能够经济高效地帮助用户分析和解决问题。
1.2 科学计算的简单处理流程
下面的流程图简单说明了科学计算的步骤。第一步是为问题设计数学模型。当创建完数学模型后,下一步是开发算法。算法通常需要利用合适的编程语言和恰当的实现框架来实现。编程语言的选择是关键决策点,由应用的性能和功能需求决定。另一个重要的决策点是确定实现算法的框架。确定了语言和框架之后,就可以实现算法并进行样本仿真了。可以对仿真的结果进行性能和准确率分析。如果实现的结果或效果不符合预期,则应该确定问题的根源。之后,需要回头改进数学模型,或者重新设计算法或它的实现,并选择合适的编程语言和框架来实现算法。
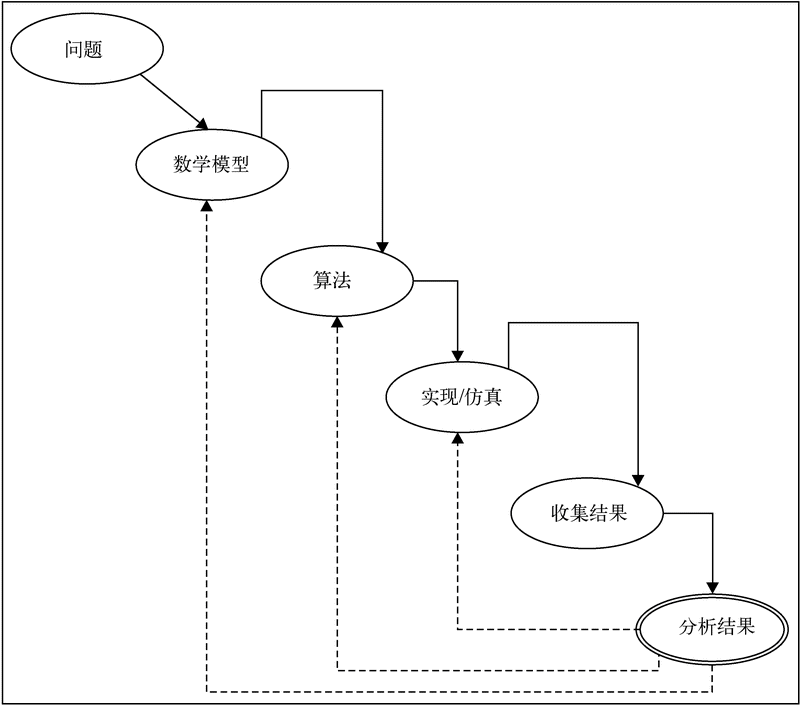
科学计算流程
数学模型表现为一组合理的数学公式,这些公式能够在一定程度上详细描述大多数问题。算法用多个步骤来表示解决过程,这些步骤需要用一种适当的编程语言或脚本来实现。
实现算法之后,还有一个重要的步骤需要完成——对实现的代码进行仿真运行。这包括设计实验基础设施、准备或整理仿真用的数据/条件、准备仿真的场景,等等。
仿真成功运行之后,下一步就是收集和展示结果以便进行分析,进而对仿真的有效性进行验证。如果结果不符合预期,就需要返回到前面的步骤改正并重复。这种返回到之前步骤的情形,在上图中用虚线表示。如果每一步都进行得很顺利,那么分析就是工作流的最后一步,图中用双线表示。
为了解决任何数学问题,尤其是科学与工程领域的数学问题而进行的算法设计与分析,称为数值分析(numerical analysis),现在也称为科学计算。在科学计算中,需要解决的问题主要是针对连续数值,而不是离散数值。后者主要指计算机科学的其他问题。通俗的表述就是,科学计算解决关于连续变量的方程和公式问题,例如时间、距离、速率、重量、高度、尺寸、温度、密度、压力、应力等。
一般情况下,连续变量的数学问题只能获得近似解,因为它们的精确解不太可能在有限的步骤中得到。因此,这些问题通过有限步的迭代处理可以收敛到一个可行解。这个可行解取决于目标问题的特性。通常迭代步骤都是有限的,每次迭代之后,结果都会更加接近仿真的期望解。仿真结果的准确性和算法的收敛速度是科学计算过程的重点。
一些科学领域已经在使用科学计算解决问题了,比如:
计算流体动力学
大气科学
地震学
结构分析
化学
磁流体力学
地质储层建模
全球海洋/气候建模
天文/天体物理
宇宙学
环境保护研究
核工程
目前,一些新兴的学科也开始借助科学计算的力量,包括:
生物学
经济学
材料研究
医学影像
动物科学
1.3 科学与工程领域的案例
让我们看几个可能用科学计算解决的问题。第一个问题是研究两个黑洞碰撞的行为,这个问题无论从理论上还是实践上都很难理解。从理论上说,这个实验非常复杂,几乎不可能在实验室实现并进行现场研究。但是这个现象可以根据爱因斯坦的广义相对论的数学公式建立合理有效的数学模型,然后在计算实验室进行仿真。然而,这个仿真需要消耗极大的计算能力,可以通过先进的分布式计算环境实现。
第二个问题与工程和设计相关。与汽车测试相关的一个问题是碰撞测试(crash testing)。为了降低完成真实(也很危险)的碰撞测试的成本,工程师和设计师们都会优先考虑进行计算机仿真碰撞测试。最后,还有大型房屋与厂房设计问题。可以按照设计目标构建一个仿真模型,但是这样做需要消耗大量的时间和金钱。然而,通过建筑设计工具完成设计可以节省大量的时间和成本。生物信息科学和医学也有类似的情况,例如蛋白质结构的折叠和传染病的建模研究。蛋白质结构折叠的研究非常耗时,但是利用大规模计算机集群和分布式计算系统可以高效地完成。类似地,在分析不同参数对传染病疫苗接种程序的影响方面,为传染病建模可以节省时间和成本。
之所以挑选这三个问题,是因为它们分别代表科学计算可以解决的三类问题。第一类问题是基本不可能解决的。第二类问题可以解决但风险很高,甚至具有严重的破坏性。第三类问题不使用仿真就可以解决,也可以在现实生活中通过模拟解决,但是通过仿真方法解决会更加经济高效。
1.4 解决复杂问题的策略
解决复杂计算问题的一个简单策略是:首先找出问题的难点,然后分解成多个小难点,各个击破,替换成问题的最优解或可行解。总之,就是要把大问题分解成小问题,分而治之。经过初步分解后的小问题,可能简单也可能依然比较复杂。可以将复杂的小问题进一步分解,直到分解成可以解决的问题为止,最终,需要解决的都是一些简单的小问题。基本思路就是通过分而治之的方法将难题替换成相似的简单问题。
在应用这个方法时,有两个关键点需要注意。首先是需要从同类问题中寻找可以解决的问题(相似性替代,切忌使用风马牛不相及的问题)。其次是问题替换之后,需要考虑最终问题是否仍然处于可接受的范围之类。现列举一些案例如下。
将无限维空间问题简化为有限维空间问题。
将无限过程转换成有限过程,例如将积分和无穷级数转换成有限项求和或有限差分法(网格法)。
如果条件允许,用代数方程代替差分方程。
将非线性问题转换成线性问题,因为后者更容易解决。
如果条件允许,将复杂的函数简化成若干简单的函数。
1.5 近似、误差及相关统计概念和术语
这些科学计算的答案通常都是近似解。近似解虽然不是我们真正想要的精确解,但是可以非常接近精确解。“非常接近”的意思是这个解十分接近实际或仿真成功获得的结果,因为它们实现了目标。这类近似解或相似解会受到许多因素的影响。影响因素按照产生阶段可以分成两类:一类是在计算开始之前就有的,另一类是在计算过程中出现的。
在计算开始之前就出现近似值,主要由以下因素造成。
建模假设或无知:建模过程中可能使用了一些假设条件,没注意或者忽略了一些概念和现象的影响,最终导致了近似或可接受的误差。
观测或实验数据:从一些低精度的设备中获取的数据可能会不准确。计算过程中使用一些常量,比如π,这些常量都是近似值,这也是造成计算结果与真实值有差距的重要原因。
计算的先决条件:输入数据是从前一个实验或仿真中获取的值,可能有点误差,而经过计算误差被进一步放大了。前一步的处理可能会成为之后实验的先决条件。
计算过程中导致近似值的主要因素如下。
简化问题:如本章前面介绍的,为了解决大而复杂的问题,需要使用分而治之的方法,并不断将小难题转换成简单问题。这可能会产生近似值。而且将无限序列替换成有限序列也可能会产生近似值。
截断和舍入:许多仿真都会对中间结果进行截断和舍入操作。类似地,计算机内部表示浮点数的方法和算术运算过程也会导致些许不准确。
科学计算最终出现近似解可能是由上面的若干因素造成的。根据不同的问题和不同的解决方法,最终结果的准确性也可能会发生变化。
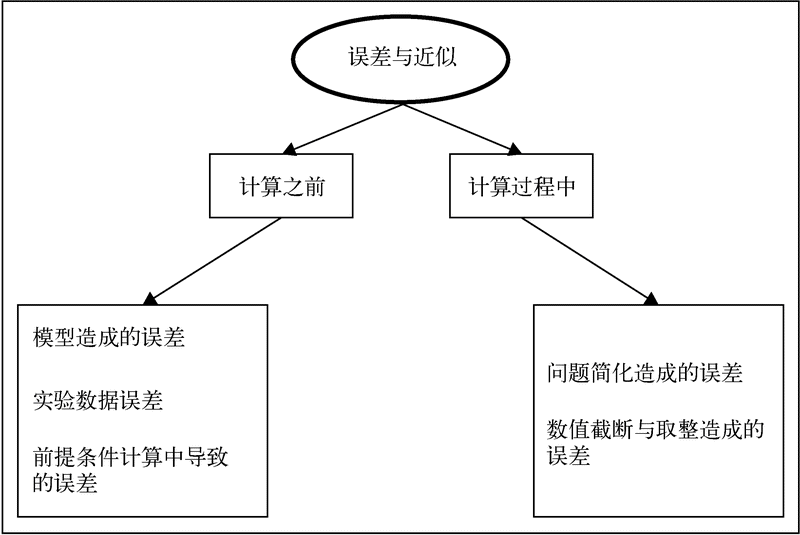
计算过程中误差与近似的分类
1.5.1 误差分析
误差分析(error analysis)是评估近似解对算法或计算过程准确性的影响程度的过程。下面将介绍误差分析的基本概念。
通过前面对近似解的讨论可以得出这样的结论:误差既可能出现在输入数据中,也可能在对输入数据的计算过程中产生。
如果进一步细分,计算误差还可以分为两类:截断误差(truncation error)和舍入误差(rounding error)。截断误差是将复杂问题简化成简单问题时造成的,例如,在得到需要的准确率之前粗略地中断算法迭代。舍入误差是使用计算机计算时数字系统表示数字精度的规则造成的,也是在对数字进行算术运算时造成的。
最终,误差究竟是十分显著还是可以忽略不计,由最终数值的规模决定。例如,误差10对数值15来说是十分显著的,但对785来说就不算大了,对17 685来说甚至可以忽略不计。通常,误差值的影响程度与结果数值具有相关性。如果知道结果数值的量级,那么看看误差值的量级,就可以判断误差究竟是可以忽略不计还是十分显著。如果误差十分显著,就要考虑引入改进手段了。
1.5.2 敏感度、稳定性和准确性
下面介绍一些问题或算法的重要属性。敏感度(sensitivity或conditioning)是问题的一种属性。在某些条件下,问题可以被称为敏感的或不敏感的,或者是良态的或病态的。如果输入值发生相对变化时,输出结果也会发生等比例的相对变化,就说问题是不敏感的或良态的。另一方面,如果输出结果发生的变化比输入值的变化幅度大,那么就认为问题是敏感的或病态的。
1.5.3 后向与前向误差估计
假设我们通过映射函数 f 对 x 进行计算获得了y,即y=f (x)。现在真实值是y,那么微量y'=y-y被称为前向误差(forward error),对应的估计方法称为前向误差分析。通常,很难获取该估计值。另一种方法是认为 y 就是同样问题带有修正 x 的精确值,即y=f ( x' )。现在x=x'-x 就被称为y 的后向误差(backward error)。后向误差分析就是对 x 的参数估计过程。
1.5.4 误差可以忽略不计吗
这个问题的答案由你准备使用科学计算的具体领域和应用场景决定。如果计算导弹的发射时间,差0.1秒都会造成严重问题。如果是计算火车的到达时间,40秒误差也不是大问题。类似地,药物剂量的一点改变可能会对病人造成极其恶劣的影响。一般情况下,如果应用场景中出现的计算误差与人的生命无关,或者不会导致巨大损失,那么可以忽略不计。否则,就需要努力解决误差的影响。
1.6 计算机算术运算和浮点数
计算机为了表示实数引入了一种科学计算的近似类型。这种近似经过实数算术运算之后会进一步放大。下面将介绍这种实数的表示、算术计算方法以及对计算结果可能产生的影响。然而,这种近似误差不仅会在计算机运算过程中出现,在手工计算过程中为了降低复杂度而采用舍入计算也会造成近似误差。
在深入介绍用计算机表示实数的方法之前,让我们先回顾一下数学中使用的科学记数法。在科学记数法中,为了将极大的数或极小的数简化成较短的形式,用近似值与10的幂数乘积表示。在科学记数法中,数字都被表示成“a 乘以10的 b 次方”,即a×10b。例如,0.000000987654和987 654可以分别表示成9.87654×10-7和9.87654×105。在科学记数法中,指数都是整数,而系数是实数,称为尾数(mantissa)。
IEEE(Institute of Electrical and Electronics Engineers,电气和电子工程师协会)在IEEE 754标准中确立了浮点数的表示方法。绝大多数主流设备都使用这套标准解决浮点数表示的相关问题。最新版标准在2008年发布,被称为IEEE 754-2008。这套标准确立了算术数据格式、交换格式、舍入规则、运算方法和异常处理。它还推荐了高级的异常处理方法、更多的运算规则、表达式估算,以及如何编写可重用的结果。
1.7 Python编程语言简介
Python是一种具有多种用途的高级编程语言,支持多种编程范式,包括过程式编程、面向对象编程、命令式编程、面向切面编程和函数式编程。Python经过扩展后还可以支持逻辑编程。Python是一种解释型语言,可以帮助开发者用比C++、Java以及其他语言更少的代码行完成同样功能的程序。Python支持动态类型和自动内存管理。Python自带一个全面的标准程序库,还有大量满足具体任务需求的第三方程序库。通过程序包管理工具,如pip、easy_install、homebrew(Mac OS X系统)、apt-get(基于Debian的Linux系统),以及其他安装工具(如Anaconda),安装Python程序包都非常容易。
Python是开源语言;它的解释器可以运行在多种操作系统上,包括Windows、Linux、OS X等系统。还有许多工具可以把Python程序编译成面向不同操作系统的可执行文件,如Py2exe和PyInstaller。可执行文件是独立代码,不需要Python解释器就能独立运行。
1.7.1 Python语言的指导原则
Guido van Rossum发明了Python,并确立了Python的指导原则,他被社区称为仁慈的独裁者(Benevolent Dictator For Life,BDFL)。Tim Peters把这些原则写成了一段偈语1(https://www.python.org/dev/peps/pep-0020/),让我们一句一句来解释。
1在Python中import this就会出现。——译者注
美观优于丑陋。(Beautiful is better than ugly.)这句话的意思是说代码是写给人看的,所以在所有程序中,代码都应该尽可能地好看,表达式语法应该简单,并且语法和风格应前后保持一致。
显明胜过隐晦。(Explicit is better than implicit.)绝大多数概念应该都是显式的,就像显式的布尔类型。我们直接用文字true和false表示布尔类型,而不需要用数字1和0表示。当然,Python也支持用数字表示布尔类型。而且非零值都可以作为布尔值。类似地,
for循环可以处理任何数据结构,不需要考虑变量类型。一个循环语句既可以遍历元组的每个元素,也可以处理字符串的每个字符。简单优于复杂。(Simple is better than complex.)Python的内存管理方式对用户而言很简单,通过垃圾回收器分配/回收内存,避免复杂操作2。另一个范例就是简洁的print语句:不仅打印时可以避免使用文件描述符,而且多个对象用逗号隔开就可以自动转换成可以打印的形式。
复杂胜过混乱。(Complex is better than complicated.)科学计算的概念都很复杂,但并非程序结构都会十分混乱。即使产品结构十分复杂,Python的程序结构也不应该杂乱无章。Pythonic方式本质上就是简单、简洁,SciPy和NumPy程序包都是非常好的例子。
扁平优于嵌套。(Flat is better than nested.)Python标准程序库提供了丰富多样的模块。由于Python的命名空间保持了扁平化结构,因此每个程序库导入名都比较简洁,例如
java.net.socket在Python里就是socket。Python标准程序库遵循自备电池(batteries included)的设计哲学。标准程序库提供的模块可以满足各种需求。例如,各种各样的网络协议模块可以用来开发丰富的网络产品。另外,标准程序库里还提供了图形用户界面编程、数据库编程、正则表达式、高精度计算、单元测试等众多模块。标准程序库里的一些模块包括网络(socket、select、SocketServer、BaseHTTPServer、asyncore、asynchat、xmlrpclib和SimpleXMLRPCServer)、互联网协议(urllib、httplib、ftplib、smtpd、smtplib、poplib、imaplib和json)、数据库(anydbm、pickle、shelve、sqlite3和mongodb)、并行处理(subprocess、threading、multipro-cessing和queue)。广泛胜过深邃。(Sparse is better than dense.)这一点是对Python标准程序库的要求,其覆盖面相对广泛浅显,而PyPI(Python package index,Python程序包索引器)则丰富多彩,博大精深,通过十分详尽的第三方程序包列表,可以为一个主题提供更深入、全面的支持。我们可以用pip安装Python程序包。
可读性不可或缺。(Readability counts.)程序的语句块都用空格创建,Python语法中使用最小的标点符号。语句结尾不需要分号。分号可以在句尾使用,但是并非必需。类似地,大多数情况下,表达式也不需要括号。Python使用内联文档产生程序API文档。Python的文档在运行时和线上都可以获取。
特例不能破坏规则。(Special cases aren't special enough to break the rules.)这句话隐含的意思是Python中每个成员都是对象。所有内置类型被设计成对象。用于表现数字的数据类型拥有方法。每个函数本身也是拥有方法的对象。
即使复杂现实会打破纯粹规则。(Although practicality beats purity.)Python支持多种编程范式,可以让用户选择最适合解决问题的范式。它支持面向对象编程、过程式编程、函数式编程等多种编程范式。
异常不能不辞而别。(Errors should never pass silently.)Python的异常处理方法,可以让异常通过较高层面的API编程解决,不需要触及底层API。Python不仅为标准异常的处理提供了非常详细的说明,同时也允许用户自定义异常,进行个性化处理。为了支持代码调试,Python提供了代码跟踪。在Python程序中,错误处理机制默认会在
stderr里把完整的错误信息打印出来。跟踪信息里包含源文件名称、行号和源代码,如果存在的话。除非需要它悄然无声。(Unless explicitly silenced.)为了应对一些特殊情况,有时也需要让异常悄无声息地运行。这时,可以使用不带
except的try语句。还有一种办法就是把异常转换成普通的字符串。模棱两可时,不要胡思乱想。(In the face of ambiguity, refuse the temptation to guess.)自动类型转换只在事先知晓的情况下才能使用,例如,整型与浮点型数据运算后生成一个浮点型数据。
应该有且仅有一种明确的方式解决问题。(There should be one—and preferably only one— obvious way to do it.)这一点是显而易见的。这就需要消除一切冗余。于是程序会变得更容易学习和记忆。
虽然那种方式起初并非显而易见,除非你是Guido。(Although that way may not be obvious at first unless you're Dutch.)上一条介绍的处理方式主要是面对标准程序库的。当然,第三方模块非常丰富。例如,Python拥有多个GUI的API,如GTK、wxPython和KDE等。网络编程工具也有很多,如Django、AppEngine和Pyramid等。
现在做比不做好。(Now is better than never.)这句话的意思是鼓励用户让Python成为他们最喜欢的工具。Python的ctypes类型,可以让Python程序使用C/C++共享程序库。
虽然不做比急于求成好。(Although never is often better than right now.)Python增强方案(Python Enhancement Proposals,PEP)提出了一种缓期执行的方案,对语法、语义和内建类型的改进都会在一段时期后发布的新版本中体现。
如果结果很难解释,一定不靠谱;如果容易解释,也许行得通。(If the implementation is hard to explain, it's a bad idea. If the implementation is easy to explain, it may be a good idea.)在Python里,所有的语法变更、新模块和API的引入,都会经过非常严谨的检查和审批流程。
2其实底层是通过引用计数等方式封装C语言的malloc和free函数。——译者注
1.7.2 为什么用Python做科学计算
说实话,如果仅从Python语言本身来看这个问题,可能其他编程语言更有优势。不过我们有NumPy、SciPy、IPython和matplotlib程序库,它们让Python成为了科学计算的最佳选择。我们将在后面的章节中介绍这些程序库。下面来总结一些Python语言和相关科学计算程序库的综合特性,这些特性让Python比其他编程语言(如MATLAB和R等)更适合做科学计算。基本上没有一种语言可以满足以下所有特性。
1. 简洁易读的代码
Python代码通常都很简洁,相比其他科学计算语言更加容易理解。正如Python指导原则中所说的,简洁是Python的设计哲学。
2. 编程范式丰富的语言设计
总的来说,Python语言的设计非常适合做科学计算,因为Python支持多种编程范式,包括过程式编程、面向对象编程、函数式编程和逻辑编程。用户可以有多种选择,可以自行确定最适合解决问题的范式。这一点在其他科学计算的编程语言中都是没有的。
3. 免费与开源
Python及其科学计算工具都可免费使用,而且都是开源的。这一点的好处是可以获取源代码。而其他大多数科学计算工具3都是独家销售的产品,其本身的算法和内容也没有向用户公开。
3R语言除外。——译者注
4. 语言交互能力
Python具有与大多数主流技术相互操作的交互能力。我们可以调用不同的编程语言的函数、代码、程序包和对象,例如MATLAB、C、C++、R、Fortran以及其他语言。还有许多方法可以实现这种交互能力,例如Ctypes、Cython和SWIG等。
5. 可移植与可扩展
Python支持绝大多数平台。因此,它是一种可移植的编程语言,而且它的程序在一个平台上写完后,迁移到另一个支持Python的平台上运行时,输出结果几乎是一样的。Python背后的设计原则使得它成为一种可以进行高度扩展的语言,这就解释了为什么我们可以拥有那么多可以解决各种任务的高级程序库。
6. 层次化模块系统
Python使用模块化系统在命名空间中以函数和类的形式组织程序。为了让Python的概念容易被人们学习和记忆,命名空间系统的设计非常简单。这么做还增强了代码的可读性与可维护性。
7. 图形用户界面程序包
Python提供了许多图形用户界面程序包和工具组合。这些工具套件和程序包可以用来做图形设计、用户界面设计、数据可视化以及许多其他与图形相关的事情。
8. 数据结构
Python支持非常全面的数据结构。数据结构在进行科学计算的程序的设计和实现过程中至关重要。Python语言的数据结构功能中最大的亮点就是词典。
9. Python的测试框架
Python的单元测试框架PyUnit具有完整的单元测试功能,可以和用户的Python程序整合在一起。它支持许多重要的单元测试概念,包括测试夹具、测试用例、测试套件和测试运行器。
10. 丰富的第三方程序库
Python认同“自备电池”的哲学,所以它的标准程序库里有丰富的程序包。作为一个可扩展的语言,Python也为不同需求的用户提供了大量成熟的个性化程序库。下面简单介绍一些用于科学计算的程序库。
NumPy/SciPy程序包可以满足科学计算中的许多数学和统计需求。SymPy程序库具有符号计算功能,可以实现基本算术、代数、积分、离散数学、量子物理等学科的符号计算。PyTables是一个高效处理拥有大量数据的数据集的程序包,通过一种分层数据库的形式(HDFS)存储数据。IPython让Python实现了交互式计算。它是一个命令行工具,同时支持多种语言的交互式计算。matplotlib程序库为Python/NumPy提供画图功能,可以画出许多的图形,例如线性图、直方图、散点图以及3D图。SQL Alchemy是一个Python编程的对象关系映射程序库。通过它,我们可以借助数据库的能力,让科学计算变得更加高效、轻松。最后,还应该介绍一个工具箱,它建立在前面介绍过的这些程序包以及其他众多开源程序库和工具箱的基础之上。这个工具箱的名字叫SageMath。它也是一个开源数学软件。
1.7.3 Python的缺点
介绍完Python相比其他科学计算语言的优越性之后,如果思考Python的缺点,会发现Python比较突出的一个缺点是它的集成开发环境(integrated development environment,IDE)没有其他语言强大。Python工具箱是把分散在各处的程序包和工具箱组合起来,其中有一些还是命令行界面。因此,就这一点来看,Python在一些平台上相比其他语言要逊色,例如Windows系统上的MATLAB。但是,这并不是说Python使用起来不方便,其实它依然很容易使用。
1.8 小结
本章首先介绍了科学计算的基本概念和定义,紧接着介绍了科学计算的操作流程,然后简要介绍了科学和工程领域的案例。之后,论述了解决复杂问题的有效策略,以及近似、误差和相关统计术语。
我们还介绍了Python语言的背景知识和指导原则,最后解释了为什么Python是进行科学计算的最佳选择。
下一章将介绍科学计算中涉及的多种数学/数值分析概念,还将介绍一些Python科学计算的程序包、工具箱和API。
