第 3 章　有效地制造与管理科学数据

第 3 章　有效地制造与管理科学数据

这一章介绍科学计算数据。首先介绍数据的基本概念，然后介绍管理数据与对数据进行不同操作的各种工具箱，之后介绍生成模拟数据的不同数据格式和基于随机数的技术。

这一章将介绍以下主题：

数据、信息与知识的基本概念
各种数据存储软件与工具的概念
可以对数据进行的操作
科学数据的标准格式
现成的数据集
用随机数生成模拟数据
大规模数据集简介

3.1　数据的基本概念

数据是关于实体的真实情况和数字的原始和未经梳理的形式。任何未经梳理/原始的数量与数值，比如一系列数字或字符，只要能够表示真实世界中的概念、现象、对象和实体，就可以视为数据。数据没有时空限制，任何地方都有数据。

数据可以被转换成信息，可以用于实现其所在组织的目标。当数据被赋予某种属性时，它就成了信息。准确及时的数据，如果按照特定的目的加以组织和准备并在特定的场景中展示出来，就可以称为信息。这样就为数据赋予了意义与实用性。

再加上专业经验，数据与信息就可以转换成知识。知识需要与具体问题相关的大量数据处理经验，例如商品定价与天气预测。

现在，让我们研究一个关于数据、信息与知识的科学案例。79°F显然只是一个温度计读数，是数据。如果为这个读数增加一些细节，例如这个温度是印度孟买印度门2015年3月3日下午5点30分的温度，那它就是信息了。根据多个年份某一周的每小时温度读数，预测下一年同一周的温度就是知识。类似地，根据印度北部过去两天下大雪的信息，预测印度中部的气温将下降几度就是知识。数据、信息与知识的关系如下图所示。这个过程是先从实验中收集数据，再从数据中提取信息，最后对信息进行细致的分析，从中获取知识。

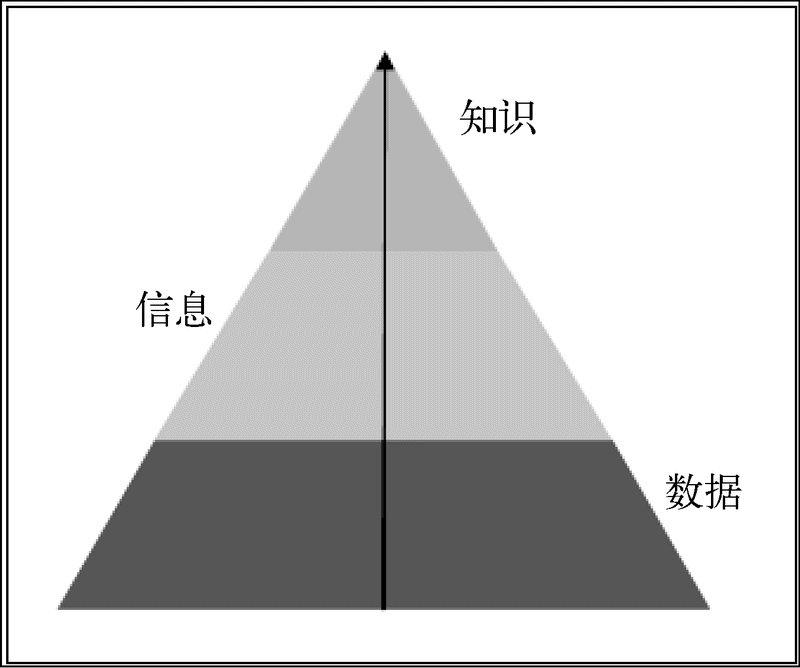
第 3 章　有效地制造与管理科学数据 - 图1

数据、信息、知识金字塔

3.2　数据存储软件与工具箱

计算机科学的概念日新月异，存储数据的软件和工具也在快速进化。目前，市面上有许多存储数据的软件和工具箱。主要有两类数据存储软件与工具箱，在每一类中还有一些子类。用于管理与存储数据的软件与工具箱分类如下图所示。

{%}

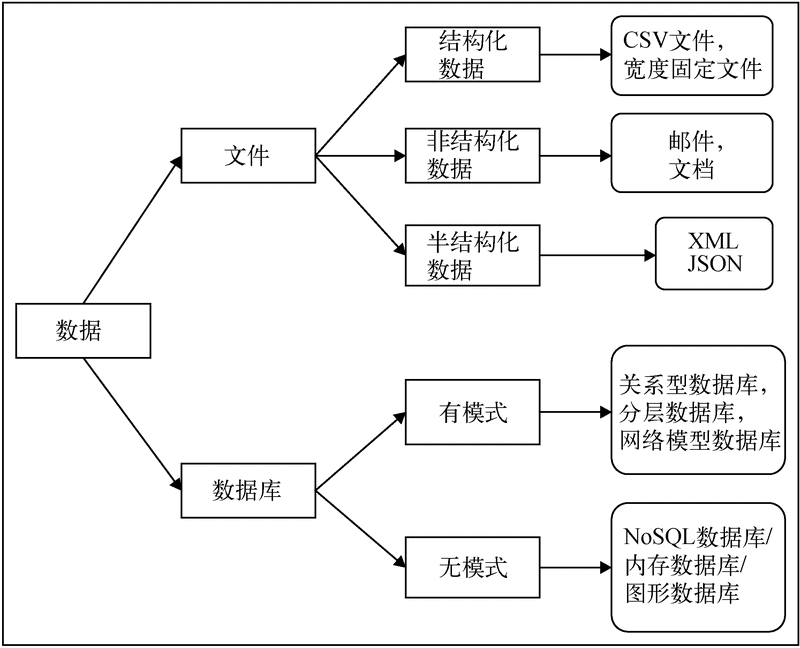
数据存储与管理的软件与工具分类

3.2.1　文件

第一种存储数据的软件与工具类型是不同格式的纯文本。纯文本文件又可以分为结构化文件与非结构化文件两种子类型。结构化文件是指按照预先设定好的固定格式存储数据。而在非结构化文件中，数据存储没有预先设定的格式。通常，这两种类型的文件都可以存储文本数据，而在一些特殊的科学软件程序中，还可以存储图像、音频、视频和其他非文本数据。

1. 结构化文件

结构化文件的一个例子是逗号分割值（comma-separated values，CSV）文本文件。在这类文件中，数据字段是通过逗号或分隔符进行区分的。分隔符可以是任字符或符号。分隔符最好不要使用存储数据中已有的符号。假如要存储财务数据，那么逗号就不适合作为分隔符。

例如下面的CSV文件：H.K. Mehta, 08-Oct-1975, Higher Education department, 50,432。

这条记录中包含姓名、出生日期、部门名称和工资。对于这个CSV文件，空格、点号（.）、逗号（,）、连字符（-）都不适合作为分隔符。如果我们选择其中之一——空格、点号、逗号或连字符——作为分隔符，那么逗号会把工资分割成两个数值，连字符会把出生日期分割成三个值，点号（.）会把姓名分割成三个值，空格会把部门名称分割成三个值。对于这条记录，分隔符可以是其他符号，例如问号（?）和管线命令（|，竖杠）。通常，在商务数据中，管线命令（|）是最常用的分隔符。

宽度固定文件（fixed-width file）是另一种结构化文件。在这类文件中，每个字段的宽度是预先设定好的，一直会保持不变。如果某个记录中的一个字段宽度比固定值小，就补空格直到达到固定宽度；如果比固定值大，就截断以满足宽度要求。

2. 非结构化文件

非结构化文件的例子包括网络服务器日志文件、图书、期刊和电子邮件。这类文件包括文本与非文本数据。文本数据是指可以用某种字符编码原则表示的数据，例如美国信息交换标准码（American Standard Code for Information Interchange，ASCII）和Unicode码。数据存储文件还有另一种类型，称为半结构化文件。这类文件不具备关系型数据库使用的常规格式。半结构化数据通过标签和其他标记区分字段，为标签赋予适当含义，从而创建记录或字段。这类数据的典型例子是XML和JSON格式。这些数据格式的优点是具有语言和系统平台独立性。因此，操作结果不会随语言与系统平台的变化而改变。

3.2.2　数据库

第二类数据存储产品是数据库。除了文件，还有许多数据库可以存储计算用的数据。数据库也可以按照有无模式分为两类：基于模式的数据库和无模式的数据库。基于模式的数据库是传统数据库，需要用户在存储数据前先创建数据对象的结构。而无模式的数据库是大型数据库领域的新方向，致力于满足大型应用程序的数据存储需求。基于模式的数据库包括MySQL、Oracle、MS SQL Server、Postgres等，无模式的数据库包括MongoDB、HBSE和Cassandra等。

3.3　常见的数据操作

除了数据存储之外，想要高效地管理与使用数据，还要执行很多操作。

数据耕耘（data farming）：利用高性能计算方法对大型数据库进行多次仿真的过程称为数据耕耘。数据耕耘的输出结果可以对数据的表层特征与深层特征进行全面的描述，它可以辅助决策制定过程。数据耕耘是一个多学科交叉的领域，包括高性能计算、数据分析与可视化以及大型数据库。
数据管理：数据管理是一个广泛的概念，由许多数据操作组成，如下所示。
- 数据治理（data governance）：这是数据管理的主要控制部分，目的是保证输入数据满足模型需要的标准格式。数据处理可以通过手工或自动化流程进行控制。
- 数据架构、分析与设计：数据架构包括数据采集所需的各种模型、流程、算法、规则与标准，以及数据存储的结构、数据集成的方法等。制定数据清洗与转换流程的相关分析与设计原则，对整个项目都是有益的。
- 数据库管理：数据库管理是一个涉及多项活动的复杂任务，包括数据库的设计与开发，数据库监控，系统整体监控，数据库性能改善，数据库能力提升与扩展计划的制定，数据安全的计划、实施与维护等。
- 数据安全管理：这包括数据安全的相关管理活动，包含接入权限的管理、数据私密性管理以及其他与数据安全相关的内容（例如数据清洗/清除、加密、覆盖与备份）。
- 数据质量管理：这是与数据质量改善相关的任务，包括许多操作，如下所示。
  - 数据清洗，对有错误或不准确的数据（即不干净的数据）进行检验与校正。
  - 数据完整性（data integrity）检验，确保不同时期与不同处理阶段的数据是准确一致的。
  - 数据质量增强（data enrichment），对数据进行精炼与增强，剔除数据中的拼写与印刷错误，改进数据质量。例如，任何时候已获取的分数都不可能超过可能的最高分。这时，我们必须改正那些分数比最高分还高的数据库记录。
  - 数据集成（data integration），是一个复杂的流程，需要丰富的经验，因为它需要将多个数据源的数据转换成统一格式，并组合在一起，而且转换过程不能影响数据的意思。
- 数据仓库管理：数据仓库管理包含数据集市的准备工作、数据挖掘与各种数据处理相关操作的实现，例如数据抽取、转换与加载（extraction, translation, and loading，ETL）操作。
- 元数据管理：这是对存储在数据库中的数据属性进行管理的过程。这些数据称为元数据（metadata）。元数据包括存储数据的描述、数据创建与修改的具体时间、数据的所有者、物理设备的位置以及其他相关细节。
数据输入与输出：任何一种应用程序都包括许多重要的操作，无论是商业产品还是科学产品。一般情况下，在进行输入与输出操作时必须小心谨慎。用户从应用程序中输出或导入数据时，需要考虑应用程序自身的特性。因此，需要使用恰当的数据格式。
科学数据存档：这个过程是指，根据应用程序和组织制定的策略中关于科学家应该存储多少数据，以及数据的接入权限等级管理的相关内容，对科学数据进行存档，以备长期使用。

3.4　科学数据的格式

Python的科学数据存储有多种格式/形式。通常，大多数的科学计算API/语言/工具包支持这些数据格式的输入和输出。这些格式中比较常用的如下所示。

网络通用数据格式（Network Common Data Form，NetCDF）：它是一种自描述、与机器/设备/平台无关、基于矩阵的科学数据格式，同时也是支持创建、访问和共享这一数据格式的函式库。它通常被捆绑于一系列的软件库中来生成和操作。通常，这种格式被用于天气预报、气候和气象上的气候变化、海洋学和GIS应用等领域。大部分GIS应用都支持NetCDF格式作为输入和输出格式，并且NetCDF还用于科学数据交换。

该格式源于美国大气科学研究大学联盟（University Corporation for Atmospheric Research，UCAR）的Unidata项目，该项目的主页由他们建设。它的网址是http://www.unidata.ucar.edu/software/netcdf/docs/faq.html。该网页对NetCDF有如下描述：

“网络通用数据格式（NetCDF）是一组对矩阵式数据接入和C语言、Fortran、C++、Java等语言的自由分发数据接入库的集合的接口。NetCDF库支持一种与机器无关的格式来表示科学数据。因此，接口、库和格式支持科学数据的生成、获取和分享。”

HDF（Hierarchical Data Format，分层数据格式）：这是一组文件格式，已演变出不同的版本（HDF4和HDF5）。HDF格式指一种为存储和处理大容量科学数据设计的文件格式及相应库文件。HDF最早由美国国家超级计算应用中心（NCSA）开发，目前在非盈利组织HDF小组的维护下继续发展。该小组确保HDF5格式的进一步发展和相关的工具/技术的发展。HDF现在受到众多商业与非商业平台的支持，包括Java、MATLAB/Scilab、Octave、IDL、Python和R。
FITS格式（Flexible Image Transport System，普适图像传输系统）：这是一种可用于存储、传输、操作科研或其他用途图片的一种数据文件格式。这种格式广泛用于天文学领域。它有好几种方式描述和元数据一起存储的光度学和空间校准信息。FITS格式的第一次标准化出台于1981年。该标准最近的版本发布于2008年。FITS也可以用于存储非图像数据，如光谱、数据立方甚至是数据库。FITS还有一个重要的特征，那就是该格式的新版本总是后向兼容的。另一个重要特征是，文件中的元数据用人类可读的ASCII码存储于头文件中。这有助于用户分析文件并理解存储于其中的数据内容。
波段交叉数据/波段交叉格式（Band-Interleaved Data/Band-Interleaved Files）：它们是二进制格式。这意味着数据被存放在非文本文件中，通常这种数据格式用于遥感和高端GIS。这些文件有两种子类型，分别是波段按行交叉格式（Band Interleaved by Line，BIL）和波段按像元交叉格式（Band Interleaved by Pixel，BIP）。
通用数据格式（Common Data Form，CDF）：这是一种存放标量和与平台无关的多维数据的数据格式。因此它被用于存放科学数据，也是一种很受研究人员和机构欢迎的数据交换格式。空间物理数据辅助系统（Space Physics Data Facility，SPDF）提供了一个CDF软件工具，作为戈达德太空飞行中心（Goddard Space Flight Center，GSFC）操作数据的工具。CDF还提供了支持各种编程语言、工具和API的良好接口，包括C、C++、C#、Fortran、Python、Perl、Java、MATLAB和IDL。

各种科学数据格式有一些共同的特征，举例如下。

这些格式支持顺序访问和随机访问数据。
它们都用于有效地存储大量的科学数据。
这些数据格式包括支持自我描述能力的元数据。
这些格式默认支持调用对象、网格、图像和N维数组。
这些格式是不可更新的。用户可以在最后添加数据。
它们都支持机器可移植性。
它们中的大部分格式都是标准化的。

这里讨论的数据格式可用于存储任意主题和其子域的数据。另外还有一些为特定主题专门设计的数据格式。下面列举了这些数据格式。这里没有给出这些数据格式的详细描述，读者可以参考它们的原始。

用于天文学领域的数据格式
- FITS：FITS天文学数据和图像格式（.fit或.fits）
- SP3：GPS和其他卫星轨道（.sp3）
用于存储医学图像数据的格式
- DICOM：DICOM标注医学图像（.dcm，.dic）
用于医学和生理学数据的格式
- Affymetrix：Affymetrix数据格式（.cdf , .cel , .chp , .gin，.psi ）
- BDF：BioSemi数据格式（.bdf）
- EDF：欧洲数据格式（.edf）
用于化学和分子生物学的数据格式
- MOL
- SDF
- SMILES
- PDB
- GenBank
- FASTA
用于地震学（与地震相关的科学和工程）的数据格式
- NDK：NDK地震学数据格式（.ndk）
用于天气数据的格式
- GRIB：GRIB科学数据格式（.grb，.grib）

3.5　现成的标准数据集

一些政府、协作组织和研究机构致力于不断地开发和维护不同主题和主题下不同领域的标准数据集。这些数据集可以供公众免费下载，或者离线工作，又或者利用这些数据集进行在线运算。一个这样重要的项目叫作开放科学数据云（Open Science Data Cloud，OSDC），它在每一个主题下都有几个数据集。现在可以获得各个开源数据源的清单了。可以通过它们的网站入口https://www.opensciencedatacloud.org/publicdata/来获取。OSDC里的一个主题数据集列表如下。

农业
- 美国农业部植物数据库
生物
- 1000个基因组
- 基因表达数据库GEO
- MIT癌症基因组数据
- 蛋白质数据银行
气候/天气
- 澳大利亚天气
- 加拿大气象中心
- UEA的气候数据（每月更新）
- 自1929年的全球气候数据
复杂网络
- 交叉引用的DOI URLs
- DBLP引用数据集
- NIST复杂网络数据集
- UFL稀疏矩阵集
- WSU图数据库
计算机网络
- 来自Common Crawl 2012年的3.5 B的网页
- 印第安纳大学100 000个用户53.5 B的网页点击信息
- CAIDA互联网数据集
- ClueWeb09的1 B网页
数据竞赛
- 机器学习中的挑战
- 关于社会福利的DrivenData竞赛
- （自2009年的）ICWSM数据挑战
- Kaggle竞赛数据
经济
- 美国经济协会（AEA）
- UMD的EconData
- 网络产品编码数据库
能源
- AMPds
- BLUEd
- Dataport
- UK-Dale
财经
- CBOE未来交易
- 谷歌财经
- 谷歌趋势
- NASDAQ
地理空间/GIS
- BODC——大约22 000变量的海洋数据
- GitHub上的剑桥、马萨诸塞州、美国、GIS数据
- EOSDIS——NASA的地球观察系统数据
- ASU的地理空间数据
医疗
- EHDP大型健康数据集
- Gapminder世界人口数据库
- 美国医疗覆盖数据库（MCD）
- 医疗数据文件
图像处理
- 2 GB的猫的图片
- 图片的情感分类
- 人脸识别基准
- MIT的大规模视觉记忆刺激
- MIT的SUN数据库
机器学习
- 查询歌手资料的月度数据
- eBay线上交易数据（2012）
- IMDb数据库
- 用于分类、回归和时间序列的Keel数据仓库
- 百万歌曲数据集
博物馆
- Cooper-Hewitt的收藏数据库
- 明尼阿波利斯艺术博物馆的元数据
- Tate收藏元数据
- Getty艺术专业名词
自然语言
- Blogger语料库
- ClueWeb09 FACC
- 谷歌图书Ngrams（2.2 TB）
- 谷歌网页5gram（2006年1 TB）
物理
- CERN开放数据入口
- NSSDC（NASA）550个航天器数据
公共领域
- CMU的JASA归档数据
- UCLA的SOCR数据集
- UFO报告
- WikiLeaks的关于911的窃听信息
搜索引擎
- UMB上分享数据的学术种子
- 互联网归档信息中的Archive-it
- DataMarket（Qlik）
- Statista.com——统计和研究
社会科学
- CMU的Enron 150个用户的电子邮件数据集
- 来源于LAW的Facebook社交网络（始于2007年）
- 2010年和2011年的Foursquare社交网络数据
- 2013年UMN/Sarwat的Foursquare数据
运动
- Betfair历史交换数据
- Cricsheet棒球比赛数据
- 1950年至今的Ergast一级方程式赛车数据（API）
- 美式足球/英式足球资源（数据和API）
时间序列
- MU的时间序列库（TSDL）
- UC河滨时间序列数据集
- 硬盘驱动失败率
交通
- 1987年至2008年的航空OD数据
- 自行车分享系统（BSS）数据集
- 湾区自行车分享数据
- 马萨诸塞州的Hubway百万骑行数据
- 海洋交通——船舶轨道、港口停靠等数据

3.6　数据生成

在一些应用中，如果用户没有现成的可用于计算的数据，那么在做计算之前就需要生成数据。数据可以用三种方法来生成：人工收集、仪器收集或通过计算机模拟（对于一些特定的应用）。

有一些应用的数据必须是人工收集的。例如，如果一个应用需要人体的生物学数据，那么可能得通过人工建立一个数据集来获得数据，而该数据集则通过采集志愿者的生物学数据来建立。这样的数据必须人工收集，无法通过电脑或仪器生成。对于这个特定的应用，用户还可以从政府部门的数据库获得数据，比如签证处理过程中收集的生物学信息，或者美国政府的个人注册数据库，又或者是印度唯一身份项目（ADHAAR）收集的数据。

对于一些特定的实验，数据可以通过一些仪器生成，这些仪器提供了用户感兴趣的指标示数。例如，与天气相关的数据可以用下列仪器生成：我们可以在不同地点放置一定数量的温度计，并周期性地收集它们的读数。用一些专用传感器，我们可以收集天气相关或健康相关的数据。例如，心率和血压相关的信息可以用戴在人身上的智能腰带或智能手表来收集。这些设备中的内置GPS系统将会周期性地用推或拉的方法收集信息。

模拟数据可以用于需要数值或文本数据的实验中，因为这些数据可以不需要特定的仪器而在电脑上直接生成。可以用一个程序生成满足预定义约束条件的数据。为了生成文本数据，可以利用已有的包含文本信息的离线文本数据或线上的网页数据，生成用于处理的新的数据样本。例如，文本挖掘和语言学处理有时需要文本样本数据。

3.7　模拟数据的生成（构造）

这一节将讨论生成模拟数据的各种方法。还将给出一个用泊松分布生成随机数的算法，以及这个算法的Python实现。此外，我们将探索不同的文本数据模拟的方法。

3.7.1　用Python的内置函数生成随机数

Python有一个叫作随机数的模块，该模块可以实现基于各种统计分布的伪随机数生成器。这个模块包括各种随机类型的函数，例如整数、序列、列表的随机排列，以及从预定义的总体中生成随机样本。Python的随机数模块支持用各种统计分布生成随机数，包括均匀分布、正态分布（高斯分布）、对数正态分布、负指数分布、伽马分布和贝塔分布。Python提供了冯·米塞斯分布（von Mises distribution），可以生成随机角度的均匀分布。Python的大部分随机数生成器模块取决于random()基本函数。这个函数在半开区间[0.0, 1.0)生成随机浮点数。

梅森旋转（Mersenne Twister）是Python中的主要随机数生成器。它能够生成53位精确的随机浮点数字，周期可达到2**19937-1。它的底层用C语言实现，所以线程安全并且速度快。它是最易扩展和测试的随机数生成器之一。但是它并不是适用于所有的应用，因为它是完全确定的。因此，它不适用于安全相关的计算。随机数模块还提供了一个SystemRandom类，这个类用操作系统自带的os.urandom()函数生成随机数。这个类可为加密目的，生成随机数。

随机模块的函数是隐藏在random.Random类中的已绑定方法。另外，用户可以拥有自己的Random类实例。好处就是这个实例并不共享状态。此外，如果用户要求生成一个新的随机数生成器，那么这个类也可以被扩展/继承来生成一个新的Random子类。在这种情况下，用户可以改写五种方法：getstate()、jumpahead()、random()、seed()和setState()。

让我们继续看看Python随机数模块的各种内置函数。这些函数在下文中将分别进行介绍。

1. 记账函数

随机数模块的各种记账函数如下。

random.seed(a=None, version=2)：这个函数初始化随机数生成器。如果用户将整数值传给a，那么这个值就是初始值。如果没有值传给a或者指定a的值是None，那么此刻的系统时间会被当作seed的值。如果操作系统支持随机资源，那么这些随机资源可以用作seed值，而不用系统时间。
random.getstate()：这个函数返回一个对象，该对象表示随机数生成器当前的内部状态1。这个对象可以用setstate()函数恢复到同样的状态。
random.setstate(state)：状态值必须是从getstate()函数调用中获得的对象。然后setstate恢复生成器的内部状态到当getstate()被调用时的状态。
random.getrandbits(k)：这个函数返回一个长度为k位（比特）的随机长整型数据。这个函数还包括MersenneTwister生成器和其他几种可选的生成器。

1保存起来可以降低后续随机数重复的概率。——译者注

2. 整型随机数生成器函数

用于返回整型随机数的不同函数如下。

random.randrange(stop)或random.randrange(start, stop[, step])：这种方法从给出的元素中返回随机选择的元素。它的参数含义如下：start是范围的起始值，该起始值包括在该范围内；stop函数是范围的终点，该终点不包括在该范围内；step表示相加的步长值以确定随机数值。
random.randint(a,b)：这个函数返回一个在a到b范围内的整型值。

3. 随机序列生成器函数

用序列操作来生成一个新的随机序列或子序列的各种函数列举如下。

random.choice(seq)：该函数返回一个非空的seq序列中的随机元素。seq字符必须是非空的。如果seq是空的，那么该函数会报错/抛出异常，即IndexError。
random.shuffle(x)：该函数混合x序列里的所有元素。混合意味着各元素的位置将在列表变量中变化。
random.sample(population, k)：这个函数返回一个总体中的k位长的唯一随机元素列表。总体必须是一个序列或集合。这个函数通常用于没有替换的随机抽样。此外，总体的各元素必须被复制，每个元素被选出组成一个列表的可能性是均等的。如果样本的大小比总体的大小k还要大，那么就会报出ValueError异常。

4. 基于统计分布的函数

有很多可以用于各种场景的统计分布。为了支持这些场景，随机数模块包括了各种统计分布的函数。下面是基于统计分布的随机数生成器。

随机数生成器函数（random.uniform(a, b)）：这个函数返回a至b区间的一个随机浮点数N。选择a至b区间的每一个随机数的概率都是一样的。
random.triangular(low, high, mode)生成器：这个函数返回服从low <= N <= high的三角分布的一个随机浮点数N。low与high是数值的边界，mode保持在边界内。默认情况下，边界最小值是0，最大值是1，mode是最大值与最小值的中点。
random.betavariate(alpha, beta)生成器：这个函数返回一个0至1区间的随机数，该随机数满足参数alpha(α)>0和beta(β)>0条件下的贝塔分布。
random.expovariate(lambd)生成器：这个函数返回一个基于指数分布的随机数。参数lambd(λ)的值必须是非零。如果lambd的值是正的，它返回0至正无穷大区间的值；如果lambd的值是负的，那么返回负无穷大到0区间的值。这个参数特意命名为lambd，因为在Python中lambda是一个保留字。
random.gammavariate(alpha, beta)生成器：这个函数基于伽马分布生成随机数，该随机数满足参数条件alpha(α)>0和beta(β)>0。
random.normalvariate(mu, sigma)生成器：该生成器基于正态分布生成随机数。这里mu(μ)是均值，sigma(σ)是标准差。
random.gauss(mu, sigma)生成器：该函数利用高斯分布生成随机数。这里mu(μ)是均值，sigma(σ)是标准差。与正态分布相比，该函数更快。
random.lognormvariate(mu, sigma)生成器：这里用对数正态分布生成随机数。以自然数为底的该分布与正态分布等价。同样，这里mu(μ)是均值，sigma(σ)是标准差。并且mu可以是任意值，而sigma必须大于0。
random.vonmisesvariate(mu, kappa)生成器：该函数用冯·米塞斯分布返回随机角度值。这里mu是角度的均值，范围在0至2*pi之间。kappa(k)是浓度参数（大于等于0）。
random.paretovariate(alpha)生成器：该函数服从帕累托分布生成随机变量。这里alpha是形状参数。
random.weibullvariate(alpha, beta)生成器：该函数用Weibull分布生成随机数。alpha是标量参数，beta是形状参数。

5. 不确定的随机数生成器

除了以上讨论的随机数生成器函数，还有一个可选的随机数生成器。该生成器被用于随机数生成器必须是不确定的情况，例如密码学和安全领域。该生成器是random.SystemRandom([seed])类。该类用操作系统提供的os.urandom()函数生成随机数。

下面的程序展示了上述提到的函数的运用。函数调用的输出也展示出来了。简便起见，我们只用到以下函数：

random.random
random.uniform
random.randrange
random.choice
random.shuffle
print random.sample
random.choice

程序如下：

import random
print random.random()
print random.uniform(1,9)
print random.randrange(20)
print random.randrange(0, 99, 3)
print random.choice('ABCDEFGHIJKLMNOPQRSTUVWXYZ') # 输出'P'
items = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
random.shuffle(items)
print items
print random.sample([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 5)
weighted_choices = [('Three', 3), ('Two', 2), ('One', 1), ('Four', 4)]
population = [val for val, cnt in weighted_choices for i in
range(cnt)]
print random.choice(population)

我们来讨论每个函数调用的输出。第一个函数random返回任意大于0小于1的浮点随机值。uniform函数返回给定范围内的均匀分布随机值。randrange函数返回一个给定范围内的随机整型值。如果第一个参数被忽略的话，那么该参数会被默认为0。因此对于randrange(20)，其范围是0~19。

现在来讨论与序列相关的函数输出。choice函数返回一个列表的随机选择值。在上面的例子中有26种选择值，而返回的值是p。shuffle函数的输出很明显，而且正如预期，其中的一些值被混合重排。sample函数选择给定大小的一个随机样本。在上面的例子中，sample的大小是5，因此随机样本有5个元素。上面程序的最后三行执行的是用一个给定的概率选择一个随机值的函数。这也是为什么choice函数被称作权重选择，因为每个选择都被赋予了一个权重。

3.7.2　基于统计分布的随机数生成器的设计和实现

本节将讨论泊松分布的算法设计和Python实现。这将有两方面的好处：一是你可以学习一个新的基于统计分布的随机数生成器的设计和实现，二是在随机模块中并不包含这个函数，所以用户也可以用到这个新分布。对于一些特定的应用，一些变量会采用泊松随机值。例如，考虑在操作系统进程调度中的调度算法。为了模拟进程调度，我们假设进程的到达遵循泊松分布。

有一些场景是可以应用泊松分布的，举例如下。

互联网的流量模式服从泊松分布。
呼叫中心接收到的呼叫数量服从泊松分布。
（有两个队参与的）曲棍球或足球比赛项目中的进球数服从泊松分布。
操作系统中的进程到达时间。
对于一个年龄段的群体，其每年的死亡率服从泊松模式。
在给定时间段内股票价格的下降次数。
对于给定片段的DNA做辐射，突变的数量服从泊松分布。

泊松分布的算法实现在高德纳的《计算机程序设计艺术（卷2）》2中给出了，其代码如下：

2此书中文版已由人民邮电出版社出版。——编者注

algorithm poisson_random_number (Knuth):
    initializations:
        L = e-λ
        k = 0
        p = 1
    do:
        k = k + 1
        u = uniform_random_number (0,1)
        p = p × u
    while p > L
        return k - 1

下面的代码是泊松分布的Python实现：

import math
import random
def nextPoisson(lambdaValue):
  elambda = math.exp(-1*lambdaValue)
  product = 1
  count = 0
  while (product >= elambda):
    product *= random.random()
    result = count
    count += 1
  return result
for x in range(1, 9):
  print nextPoisson(8)

上面程序的输出是：

　关于重现随机数的特别提示

如果一个应用要求用任意方法重现随机数，在这种情况下，我们可以用这些函数重现生成的随机数。为了重现序列，需要用到同样的函数和同样的种子值。同样，我们也可以重现列表，这也是为什么我们称大多数随机数生成函数是确定的。

3.7.3　一个用简单逻辑生成5位随机数的程序

以下程序展示了用时间和日期对象生成随机数的方法。它用了特别简单的逻辑来生成5位随机数。在这个程序中，用当前的系统时间来生产随机数。系统时间的4个组件——小时、分钟、秒和毫秒——通常是唯一的组合。这个值被转换成一个字符串，然后转换成一个5位的值。在用户定义的函数的第一行，引入了一个毫秒级的延迟，这样在很短的时间内，每次调用时，时间值是不同的。如果没有这一行，用户将得到一些重复的值。

import datetime
import time
# 用户定义函数返回5位的随机数
def next_5digit_int():
    # 这样可以将随机数设置为微秒级
    time.sleep(0.123)
    current_time = datetime.datetime.now().time()
    random_no = int(current_time.strftime('%S%f'))
    # 去掉后三位尾数
    return random_no/1000
# 随机数生成演示
for x in range(0, 10):
    i = next_5digit_int()
    print i

3.8　大规模数据集的简要介绍

科学应用程序的数据集范围很广泛，从几MB到几GB都有。某些特殊应用程序的数据集非常大，可能有几PB（拍字节）3。以我们熟悉的MB与GB来对比一下PB的规模。假如我们把1 PB的数据刻录成CD，然后把这些CD堆起来，那么叠起来的光盘高度大约是1.75千米。由于近些年网络和分布式计算技术的进步，有许多应用需要处理PB的数据量。为了有效地处理大规模数据集，在软件和硬件层面都出现了一些解决方法。

31 PB=1024 TB。——译者注

有一些处理各种规模数据集的有效架构。这些架构在处理小规模、中等规模和大规模数据时同样高效，仅取决于提供的基础架构。MapReduce就是这样一种架构，Hadoop是MapReduce架构的一个开源实现。

在数据库层面，用户有多种方法来存储和管理任意规模的数据。这些数据库可能是最简单的，如纯文本文件（文本文件或者二进制文件）。然后还有一些基于模式的数据库，如关系型数据库，这些数据库能高效地管理几个GB的数据库。文件数据库和基于模式的数据库都可以管理MB到GB规模的数据。为了处理超过这个限制的数据，现在的趋势是用非基于模式的数据库和高级分布式文件系统，例如谷歌的BigTable、Apache HBase和HDFS。HBase是一个基于列的数据库，可以支持超大规模数据库。HDFS是一个分布式文件系统，它能存储几个PB的文件，不像普通文件系统（如WINDOWS NT）的最大文件大小16 GB。

大多数编程语言都支持这些框架和数据库，包括Python、Scala、Java、Ruby等。除了软件级的，还有一些复杂的硬件组合，例如不同硬件（如处理器、I/O设备和网络设备）组成的虚拟化内容。还有一些专门针对之前介绍的数据库软件的性能增强硬件。

分布式计算领域最新的进展称为云计算，它包括一些新的科学计算和商业应用。云计算和上面讨论的一些概念的运用，为人们提供了有史以来最大的数据处理和存储能力，让一切成为可能。在云计算环境中正不断地产生新应用，这些新的应用的数量与日俱增。

以上讨论的技术也用于文本搜索、模式查找和匹配、图像处理、数据挖掘和大数据集的计算。在各种商业和科学应用中，这些需求非常普遍。

在第8章中，我们将详细讨论这些技术，并重点关注它们在大规模科学项目中的应用。

3.9　小结

本章首先介绍了数据、信息和知识的基本概念，然后介绍了各种用于存储数据的软件，之后讨论了数据集的各种操作，列举了存储科学数据的标准格式。接着还讨论了各主题领域的各种预定义的、已使用的标准数据集。但是，目前仍然有一些特定主题的数据集是缺失的。

在介绍基本概念之后，本章还介绍了各种为特定实验模拟数据的技术。还介绍了用于随机数生成的各种标准函数。对于模拟数据的生成，我们还介绍了用泊松分布生成随机数的一个算法和一个程序。

下一章将详细介绍Python科学计算的API和工具。这些API提供数值计算（NumPy和SciPy）、符号计算（SymPy）、数据可视化和画图（matplotlib和pandas）以及交互式编程（IPython）。此外，还会简单讨论这些API的特征和功能。

第 3 章 有效地制造与管理科学数据

第 3 章 有效地制造与管理科学数据

3.1 数据的基本概念

3.2 数据存储软件与工具箱

3.2.1 文件

3.2.2 数据库

3.3 常见的数据操作

3.4 科学数据的格式

3.5 现成的标准数据集

3.6 数据生成

3.7 模拟数据的生成（构造）

3.7.1 用Python的内置函数生成随机数

3.7.2 基于统计分布的随机数生成器的设计和实现

3.7.3 一个用简单逻辑生成5位随机数的程序

3.8 大规模数据集的简要介绍

3.9 小结

第 3 章　有效地制造与管理科学数据

第 3 章　有效地制造与管理科学数据

3.1　数据的基本概念

3.2　数据存储软件与工具箱

3.2.1　文件

3.2.2　数据库

3.3　常见的数据操作

3.4　科学数据的格式

3.5　现成的标准数据集

3.6　数据生成

3.7　模拟数据的生成（构造）

3.7.1　用Python的内置函数生成随机数

3.7.2　基于统计分布的随机数生成器的设计和实现

3.7.3　一个用简单逻辑生成5位随机数的程序

3.8　大规模数据集的简要介绍

3.9　小结