第 4 章　Python科学计算API

本章将对Python各种科学计算API和工具箱的特性与能力进行全面的介绍。除了介绍基础知识，我们还会针对每个API演示一些示例程序。由于符号计算是计算机数学中一个比较特殊的领域，因此我们在SymPy那一节中安排了一个小节单独介绍计算机代数系统的基础知识。

本章将介绍的主题如下：

  • 用NumPy和SciPy做科学数值计算

  • 用SymPy做符号计算

  • 计算机代数系统

  • SymPy及其模块介绍

  • SymPy示例程序

  • 数据分析、可视化与交互式计算

4.1　Python数值科学计算

科学计算主要需要的是完成代数方程、矩阵、微分、积分、微分方程、统计、方程求解等方面计算的能力。Python语言本身并不具有这些功能。但是，NumPy和SciPy的发展让我们能够完成这些计算，并提供了更多的高级功能。NumPy和SciPy都是非常强大的Python程序包，让用户可以高效地完成各种科学应用需要的计算任务。

4.1.1　NumPy程序包

NumPy是Python科学计算的基础程序包。它提供了多维数组和基本数学运算的功能，比如线性代数。Python提供了一些数据结构来存储用户数据，最流行的数据结构是列表和字典。列表可以存储任意Python对象作为元素。这些元素可以通过for循环或迭代器进行处理。字典对象以键值对的形式存储数据。

1. N 维数组数据结构

N维数组（NumPy的ndarray对象）与列表类似，但是更加灵活高效。N 维数组是一个数组对象，可以表示固定数量的多维数组。这个数组应该是齐次的（homogeneous）。它通过dtype类型的对象定义数组中元素的数据类型。这个对象可以定义数据的类型（整型、浮点型或Python对象类型）、数据的字节数以及字节存储顺序（byte ordering，包括big-endian高位至低位与little-endian低位至高位）。另外，如果数据类型是record或sub-array，类型还会包含具体的细节信息。真实的数组可以通过numpy.array、numpy.zeros、numpy.empty三种方法创建。

N 维数组另一个重要特性是数组大小是可以动态调整的。而且如果用户需要从数组中移除一些元素，可以通过NumPy的模块实现戴面具数组（masked array）。在许多科学计算场景中，人们都需要删除/清理异常数据。numpy.ma模块能够实现为数组戴面具的功能，轻松地移除数组中的元素。戴面具数组就是正常数组加了一个面具（mask）。面具其实是另一个由True和False构成的数组。对于某个位置的元素，如果面具数组中的值是True，那么原数组对应位置的值就是有效的；如果面具数组中的值是False，那么原数组对应位置的值就是无效的或隐藏的。对于原数组中那些标记为False的数值而言，N 维数组上进行任何计算时，都不会考虑这些被隐藏的元素。

2. 文件处理

科学计算的另一个重要方面是用文件存储数据。NumPy可以对文本文件和二进制文件进行读写操作。大多数情况下，文本文件都是读取、写入和进行数据交换的良好格式，因为它们天生具有移植性，而且大多数系统平台都自带文本文件的处理功能。但是，对于一些应用程序而言，有时用二进制文件更好，或者在一些场景中，这些应用程序需要的数据只能存储成二进制文件格式。有时，数据的大小和类型决定了存储形式，例如图像和声音文件只能存储成二进制文件。

相比文本文件，二进制文件较难管理，因为它们的格式特殊。而且二进制文件的大小都相对非常小，对它们的读/写速度比文本文件更快。快速的读/写最适用于那些需要处理大型数据集的应用程序。用NumPy操作二进制文件的唯一缺点是，它们只能通过NumPy接入。

Python的文本文件操作函数包括open、readlines、writelines。但是，用这些函数操作科学数据的性能并不佳。这些Python函数在从文件读写数据时非常慢。NumPy有一组高性能函数，可以在计算之前将数据载入 N 维数组。在NumPy中，文本文件可以通过numpy.loadtxt和numpy.savetxt函数接入。loadtxt函数可以将文本文件的数据载入 N 维数组。NumPy还有一个独立的函数用于操作二进制数据。这些函数分别是读取用的numpy.load和写入用的numpy.save。

3. 简单的NumPy程序

NumPy数组可以从使用数组的列表或元组创建。这个方法可以将序列的序列转换成二维数组：

  1. import numpy as np
  2. x = np.array([4,432,21], int)
  3. print x   #输出[ 4 432 21]
  4. x2d = np.array( ((100,200,300), (111,222,333), (123,456,789)) )
  5. print x2d

输出结果如下：

  1. [  4 432  21]
  2. [[100 200 300]
  3. [111 222 333]
  4. [123 456 789]]

基本的矩阵算术运算都可以在二维数组上简单地完成，如下面的程序所示。这些运算基本都是应用在元素上。因此，操作符两侧的数组必须是同样维度的。如果维度不一致，运算就会引起运行时错误。下面的程序示例演示一维数组的算术运算：

  1. import numpy as np
  2. x = np.array([4,5,6])
  3. y = np.array([1,2,3])
  4. print x + y    # 输出[5 7 9]
  5. print x * y    # 输出[ 4 10 18]
  6. print x - y    # 输出[3 3 3]
  7. print x / y    # 输出[4 2 2]
  8. print x % y    # 输出[0 1 0]

有一个单独的matrix子类可以进行矩阵运算。让我们用下面的程序示例演示矩阵运算，对比数组乘法与矩阵乘法的差异。NumPy的矩阵是二维的，而NumPy数组可以是任意维度的：

  1. import numpy as np
  2. x1 = np.array( ((1,2,3), (1,2,3), (1,2,3)) )
  3. x2 = np.array( ((1,2,3), (1,2,3), (1,2,3)) )
  4. print "First 2-D Array: x1"
  5. print x1
  6. print "Second 2-D Array: x2"
  7. print x2
  8. print "Array Multiplication"
  9. print x1*x2
  11. mx1 = np.matrix( ((1,2,3), (1,2,3), (1,2,3)) )
  12. mx2 = np.matrix( ((1,2,3), (1,2,3), (1,2,3)) )
  13. print "Matrix Multiplication"
  14. print mx1*mx2

输出结果如下：

  1. First 2-D Array: x1
  2. [[1 2 3]
  3.  [1 2 3]
  4.  [1 2 3]]
  5. Second 2-D Array: x2
  6. [[1 2 3]
  7.  [1 2 3]
  8.  [1 2 3]]
  9. Array Multiplication
  10. [[1 4 9]
  11.  [1 4 9]
  12.  [1 4 9]]
  13. Matrix Multiplication
  14. [[ 6 12 18]
  15.  [ 6 12 18]
  16.  [ 6 12 18]]

下面的简单程序演示了NumPy的简单统计函数：

  1. import numpy as np
  2. x = np.random.randn(10)      # 创建一个有10个随机元素的数组
  3. print x
  4. mean = x.mean()
  5. print mean
  6. std = x.std()
  7. print std
  8. var = x.var()
  9. print var

第一个样本的输出结果如下：

  1. [0.08291261  0.89369115  0.641396  -0.97868652  0.46692439
  2.  -0.13954144
  3.  -0.29892453  0.96177167  0.09975071  0.35832954]
  4. 0.208762357623
  5. 0.559388806817
  6. 0.312915837192

第二个样本的输出结果如下：

  1. [ 1.28239629  0.07953693  -0.88112438  -2.37757502  1.31752476
  2.   1.50047537
  3.   0.19905071  -0.48867481  0.26767073   2.660184 ]
  4. 0.355946458357
  5. 1.35007701045
  6. 1.82270793415

上面的程序都是一些简单的NumPy示例。我们将在第5章中详细地介绍NumPy的功能。下一节介绍Python的SciPy程序包。

4.1.2　SciPy程序包

SciPy是对Python的NumPy的功能扩展，它提供了许多高级数学函数，例如微分、积分、微分方程、优化方法、数值分析、高级统计函数、方程式求解等。SciPy是在NumPy数组框架的基础上实现的。它对NumPy数组和基本的数组运算进行扩展，满足科学家和工程师解决问题时需要用到的大部分数学计算功能。

这一章将介绍一些SciPy基本功能的程序示例，NumPy和SciPy的功能将在第5章中详细介绍。下面几个小节将介绍SciPy的一些重要程序包/模块的基础知识，包括聚类分析、文件处理、积分、数值分析、优化方法、信号与图像处理、空间分析和统计学。

1. 优化函数程序包

SciPy的优化程序包提供了解决单变量和多变量的目标函数最小值问题的功能。它可以通过大量的算法和方法解决最小化问题。最小化问题在科学与商业领域中十分普遍。一般情况下，我们会使用线性回归，搜索函数的最大值与最小值，求方程的根，通过线性规划方法求解，等等。优化函数程序包支持所有这些功能。

2. 数值分析程序包

数值分析程序包实现了大量的数值分析算法和方法，都作为内置函数。它支持单变量和多变量的插值，以及一维和多维的样条插值。当数据受单变量影响时，用单变量插值；当数据收到多个变量的影响时，用多变量插值。除了这些功能之外，数值分析程序包还提供了拉格朗日（Lagrange）和泰勒（Taylor）多项式插值方法。

3. 积分与微分方程

积分是科学计算中的重要数学工具。SciPy的积分程序包提供了数值积分的功能。SciPy提供了大量的函数解决积分方程与数据的计算问题。它还提供了常微分方程的积分工具。它还借助大量数值分析得数学方法完成数值积分的计算。

4. 统计学模块

SciPy的统计学模块提供了大量的概率分布函数和统计函数。它支持的概率分布函数包括连续变量分布函数、多变量分布函数以及离散变量分布函数。统计函数包括简单的均值到复杂的统计学概念，包括偏度（skewness）、峰度（kurtosis）、卡方检验（chisquare test）等。

5. 聚类程序包与空间算法

聚类分析是一项流行的数据挖掘技术，在科学与商业领域有广泛的应用。在科学领域中，生物学、粒子物理学、天文学、生命科学与生物信息学都是一些广泛使用聚类分析解决问题的领域。聚类分析在计算机科学的诸多领域也应用广泛，例如计算机欺诈检测、安全分析与图像处理等。聚类程序包提供了K-means聚类、向量量化（vector quantization）1、层次聚类（hierarchical clustering）与凝聚式聚类（agglomerative clustering）函数等。

1将一个范围内的值用一个值近似替代。——译者注

spatial类利用三角函数、沃罗诺伊图（Voronoi Diagram）以及多点的凸包（Convex Hull）分析空间中两点之间的距离。它还用KD树算法实现了RNN函数。

6. 图像处理

SciPy提供了大量的图像处理函数，包括基本的图像文件读/写、图像显示，以及简单的处理函数，例如裁剪、翻转和旋转。它还支持图像过滤函数，包括图像数学变换、平滑、降噪、锐化。另外，它还支持许多其他操作，如通过不同对象的像素进行图像分割、分类，以及通过边缘检测进行特征提取。

4.1.3　简单的SciPy程序

以下几个小节将介绍一些用SciPy模块和程序包实现的程序示例。首先将介绍一个用SciPy进行标准统计计算的示例，然后是一个用优化方法寻找函数最小值的程序，最后介绍一个图像处理程序。

1. 用SciPy做统计

SciPy的统计学模块有完成简单统计学运算的函数和各种各样的概率分布函数。下面的程序用SciPy的stats.describe函数演示了简单的统计运算。这个函数可以处理数组，返回数组元素的数量、最小值、最大值、均值、方差、偏度和峰度：

  1. import scipy as sp
  2. import scipy.stats as st
  3. s = sp.randn(10)
  4. n, min_max, mean, var, skew, kurt = st.describe(s)
  5. print("Number of elements: {0:d}".format(n))
  6. print("Minimum: {0:3.5f} Maximum: {1:2.5f}".format(min_max[0],
  7.     min_max[1]))
  8. print("Mean: {0:3.5f}".format(mean))
  9. print("Variance: {0:3.5f}".format(var))
  10. print("Skewness : {0:3.5f}".format(skew))
  11. print("Kurtosis: {0:3.5f}".format(kurt))

输出结果为：

  1. Number of elements: 10
  2. Minimum: -2.00080 Maximum: 0.91390
  3. Mean: -0.55638
  4. Variance: 0.93120
  5. Skewness : 0.16958
  6. Kurtosis: -1.15542

2. SciPy优化函数

在数学优化理论中，一种被称为Rosenbrock的非凸函数常用于检测优化算法的性能。以下程序演示了该函数的最小值问题。N 个变量的Rosenbrock函数方程如下所示，它在xi =1时最小值为0：

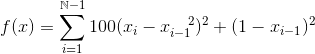
f(x)=\sum^{\mathbb{N}-1}_{i=1}100(x_i-x_{i-1}^{~~~2})^2+(1-x_{i-1})^2

上面方程的程序如下所示：

  1. import numpy as np
  2. from scipy.optimize import minimize
  4. # 定义Rosenbrock函数
  5. def rosenbrock(x):
  6.     return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)
  8. x0 = np.array([1, 0.7, 0.8, 2.9, 1.1])
  9. res = minimize(rosenbrock, x0, method = 'nelder-mead', options =
  10.         {'xtol': 1e-8, 'disp': True})
  12. print(res.x)

输出结果为：

  1. Optimization terminated successfully.
  2.          Current function value: 0.000000
  3.          Iterations: 516
  4.          Function evaluations: 827
  5. [ 1.  1.  1.  1.  1.]

最后一行是print(res.x)的输出结果，可以看出里面的元素都是1。

3. SciPy图像处理

下面两个程序演示SciPy的图像处理功能。第一个程序显示标准测试图像，这张图像名叫Lena，广泛应用于图像处理领域。第二个程序演示图像几何变换，它会完成图像裁剪和45度旋转。

下面的程序是用matplotlib的API显示Lena图像。imshow方法会把 N 维数组渲染为图像，show显示图像：

  1. from scipy import misc
  2. l = misc.lena()
  3. misc.imsave('lena.png', l)
  4. import matplotlib.pyplot as plt
  5. plt.gray()
  6. plt.imshow(l)
  7. plt.show()

这个程序的输出结果如下图所示。

{%}

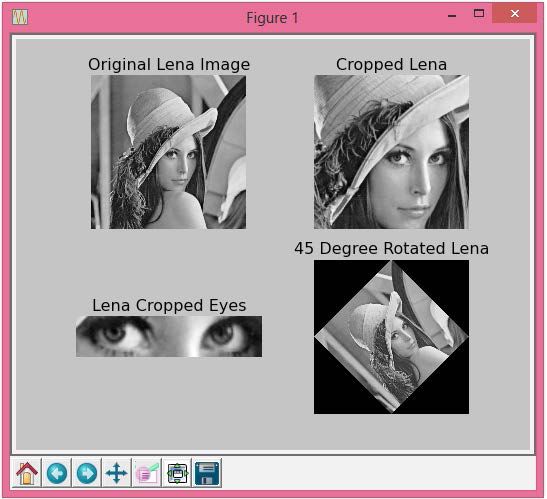
下面的程序完成图像的几何变换。变换后的图像与原始图像共同放在一个2×2的数组中：

  1. import scipy
  2. from scipy import ndimage
  3. import matplotlib.pyplot as plt
  4. import numpy as np
  6. lena = scipy.misc.lena()
  7. lx, ly = lena.shape
  8. crop_lena = lena[lx/4:-lx/4, ly/4:-ly/4]
  9. crop_eyes_lena = lena[lx/2:-lx/2.2, ly/2.1:-ly/3.2]
  10. rotate_lena = ndimage.rotate(lena, 45)
  12. # 四幅图，返回二维数组
  13. f, axarr = plt.subplots(2, 2)
  14. axarr[0, 0].imshow(lena, cmap=plt.cm.gray)
  15. axarr[0, 0].axis('off')
  16. axarr[0, 0].set_title('Original Lena Image')
  17. axarr[0, 1].imshow(crop_lena, cmap=plt.cm.gray)
  18. axarr[0, 1].axis('off')
  19. axarr[0, 1].set_title('Cropped Lena')
  20. axarr[1, 0].imshow(crop_eyes_lena, cmap=plt.cm.gray)
  21. axarr[1, 0].axis('off')
  22. axarr[1, 0].set_title('Lena Cropped Eyes')
  23. axarr[1, 1].imshow(rotate_lena, cmap=plt.cm.gray)
  24. axarr[1, 1].axis('off')
  25. axarr[1, 1].set_title('45 Degree Rotated Lena')
  27. plt.show()

输出结果如下。

{%}

SciPy和NumPy之所以成为Python科学计算的核心，是因为它们为数值计算提供了坚实的基础功能。我们将在第5章介绍两个软件包的细节。下一节内容介绍用SymPy做符号计算。

4.2　SymPy符号计算

计算机直接对数学符号进行正确的计算被称为符号计算。通常，符号计算也被称为计算机代数，而对应的计算机系统称为计算机代数系统。下面将对SymPy程序库作简单介绍。我们将在第6章中深入介绍用Python做符号计算的内容。

4.2.1　计算机代数系统

下面介绍计算机代数系统（Computer Algebra System，CAS）的概念。CAS是一个软件或者工具箱，用计算机代替手工运算数学表达式2。早期用计算机解决这类问题称为计算机代数，现在称为符号计算。CAS可以分为两类：一类是通用CAS，另一类是解决特殊问题的专用CAS。通用CAS可以应用于大多数代数领域，而专用CAS是面向某个具体领域的，如群论和数论。在大多数科学计算问题中，我们都使用通用CAS计算数学表达式。

2如商业数学软件Mathmatics。——译者注

4.2.2　通用CAS的特点

科学计算中使用的通用CAS具有以下特点。

  • 具有操作数学表达式的用户界面。

  • 编程与调试的界面。

  • 该系统需要对不同的数学表达式进行简化。因此，简化器（simplifier）是CAS系统的核心组件。

  • 通用CAS必须支持大量的数学函数，才能完成任意代数计算需要的数学功能。

  • 大多数场景中计算量都很大，所以内存管理至关重要。

  • 系统必须支持高精度与大数计算。

4.2.3　SymPy设计理念简介

SymPy是Python版的开源计算机代数系统实现。SymPy的设计理念是设计与开发一套功能齐全的CAS，代码尽可能简单，保持高度的易扩展性。它是纯Python代码写的，没有任何第三方库。

SymPy的基本思路是创建与操作数学表达式。用户借助SymPy可以用Python语言写数学表达式——通过SymPy类和对象。这些表达式由数字、符号、运算符、函数等构成。函数都是一些实现数学功能的模块，如对数函数与三角函数。

SymPy的开发是Ondřej Čertík从2006年8月开始的。此后，不断有开发者加入项目，规模达到了几百人。现在这个程序库包括26个模块。这些模块可以满足常用的计算需求，如符号计算、积分、代数、离散数学、量子物理、画图与打印等，计算结果还可以输出为LaTeX或其他格式。

SymPy的能力可以分为两类——核心能力和高级能力，因为SymPy程序库分为一个核心模块和多个高级可选模块。这些由不同模块支持的能力介绍如下。

1. 核心能力

核心能力模块支持数学代数运算需要的基本功能。这些运算包括基本算术运算，如加减乘除和幂运算。核心模块还具有数学式简化的能力，可以对复杂的数学式进行简化。它也提供了级数与符号展开的能力。

核心模块还支持三角函数、双曲线、指数函数、方程根求解、多项式、阶乘、伽玛函数、对数函数等功能，以及B—样条曲线、球面调和函数、张量函数和正交多项式等特殊函数。

核心模块中还有强大的模式匹配运算支持。另外，SymPy的核心能力还有代数运算的等价替换功能。它不仅支持整数、有理数、浮点数的高精度算术运算，还支持多项式运算中的非可交换变量和符号。

2. 多项式

多项式模块中有大量的函数处理多项式运算。这些函数包括多项式除法、最大公约数（greatest common divisor，GCD）、最小公倍数（least common multiplier，LCM）、无平方因式分解（square-free factorization）、带符号系数（symbolic coefficient）的多项式表示。还有一些特殊功能，如合矢量的计算、三角恒等式的推导、部分分式分解、Gröbner基（Gröbner basis）的多项式环和域。

3. 微积分

微积分模块中有大量的基础与高级微积分运算功能的支持。它有一个limit函数，可以设置积分上下限。它还支持导数、积分、级数展开、微分方程以及有限差分运算。SymPy还支持定积分与积分变换。在微分中，还支持数值微分、复合导数与分数阶导数。

4. 方程式求解

求解器（solver）是SymPy中求方程式解的模块。这个模块具有解复数多项式、多项式的根以及多项式组的能力。它有一个函数可以解代数方程式。它不仅可以解微分方程问题（包括常微分方程、偏微分方程、初始值与边界值的问题等），还可以解差分方程。在数学上，差分方程也称为递归关系式，也就是方程递归地定义序列与多维数组的值。

5. 离散数学

离散数学指变量特征是离散的数学分支，与连续变量的数学（微积分）区分开来。它主要处理整数、图形，以及逻辑学中的观点问题。这个模块对二项式系数、乘积与求和运算有完整的支持。

这个模块还支持数论中的许多函数，包括残差理论、欧拉公式、分割理论以及处理质数与因数分解的许多函数。SymPy还支持利用符号与布尔值来创建和操作逻辑表达式。

6. 矩阵

SymPy具有强大的矩阵与行列式计算的功能。矩阵属于线性代数的数学分支。SymPy支持矩阵创建、基本运算（如乘法与加法）、全0矩阵与全1矩阵、随机矩阵以及针对矩阵元素进行的运算。它还支持一些特殊函数，如计算海森矩阵（Hessian matrix）的函数、一组向量的格拉姆—施密特（GramSchmidt）正交化函数、朗斯基行列式（Wronskian）计算的函数，等等。

另外，SymPy还支持特征值和特征向量的计算、矩阵转置，以及矩阵与行列式求解。还支持矩阵的行列式计算，支持Bareis因式分解算法和Berkowitz算法等。矩阵计算中，还有零空间（null space）计算（方程式求解）、矩阵代数余子式展开（cofactor expansion）工具、矩阵元素求导数以及对偶矩阵。

7. 几何

SymPy有支持二维空间各种运算的模块，可以创建点、线、圆、椭圆、多边形、三角形、射线和线段等常见的二维对象。我们还可以直接查询对象的属性，例如部分对象的面积（椭圆、圆和三角形）和直线之间的交点。它还可以查询对象间的相切、相似与相交属性。

8. 画图

SymPy中有个模块可以画出二维图与三维图。现在图形底层都是用matplotlib软件包，也支持TextBackend、Pyglet和textplot等软件包。SymPy还提供了很好的自定义图形与画不同几何图形的交互接口。

画图模块的画图功能如下所示：

  • 二维直线图

  • 二维可变参数图

  • 二维隐式与区域图

  • 双变量三维图

  • 三维直线与曲面图

9. 物理学

SymPy有一个模块可以解决物理学问题。它支持力学功能，包括经典力学与量子力学以及高能物理学。它还支持一维空间与三维空间的泡利代数与量子谐振子。还有光学相关的功能。还有一个独立的模块将物理单位集成到SymPy里。用户可以选择相应的物理单位完成计算和单位转换。这个单位系统是由物理单位与常量构成的。

10. 统计学

SymPy的统计学模块支持数学计算中涉及的许多统计函数。除了常见的连续与离散随机分布函数，它还支持符号概率相关功能。SymPy里的随机分布函数都支持随机数生成的功能。

11. 打印

SymPy有一个模块可以提供漂亮的打印功能。漂亮打印包括对不同文体格式的支持，如源代码、文本文件、标记语言文件以及其他内容。这个模块可以通过ASCII和Unicode生成各种文字。

它支持不同的打印机，如LaTeX和MathML打印机。可以打印多种编程语言生成的源代码，如C、Python和Fortran。还可以打印用标记语言，如HTML和XML格式，生成的内容。

4.2.4　SymPy模块

下面的列表是前面讨论到的模块的名称。

  • Assumptions：假设引擎

  • Concrete：符号积和符号总和

  • Core basic class structure：基本的、加、乘、指数等

  • Functions：基本的函数和特殊的函数

  • Galgebra：几何代数

  • Geometry：几何实体

  • Integrals：符号积分

  • Interactive：交互会话（如IPython）

  • Logic：布尔代数和定理证明

  • Matrices：线性代数和矩阵

  • mpmath：快速的任意精度的数值运算

  • ntheory：数论函数

  • Parsing：数学的和最大化的句法分析

  • Physics：物理单位和量子相关

  • Plotting：用Pyglet进行二维和三维的画图

  • Polys：多项式代数和因式分解

  • Printing：漂亮的打印和代码生成

  • Series：符号极限和截断的序列

  • Simplify：用其他形式改写表达式

  • Solvers：代数、循环和差分

  • Statistics：标准概率分布

  • Utilities：测试架构和兼容性相关的内容

在各种数学工具箱中有多种符号计算系统可供使用。有如Maple和Mathematica这样的商业软件，也有如Singular和AXIOM这样的开源软件。但是这些产品有它们自身的脚本语言。很难扩展它们的功能，并且这些软件的开发周期也很慢。而SymPy高度可扩展，它由Python设计和开发，是一个开源的支持快速开发周期的API。

4.2.5　简单的范例程序

这里用一些非常简单的示例来帮助你理解SymPy的能力。这些不到10行的SymPy源代码包含了从基本符号操作到极限、差分和积分等主题。我们可以使用谷歌App引擎上的在线运行的SymPy来运行这些SymPy程序，其网址是http://live.sympy.org/。

1. 基本符号操作

下面的程序定义了三种符号和用这些符号组成的一个表达式，之后打印了这个表达式：

  1. import sympy
  2. a = sympy.Symbol('a')
  3. b = sympy.Symbol('b')
  4. c = sympy.Symbol('c')
  5. e = ( a  b  b + 2  b  a  b) + (a  a + c * c)
  6. print e

输出结果是：

  1. a**2 + 3*a*b**2 + c**2

这里**表示指数运算。

2. SymPy的表达式扩展

下面的程序展示了表达式扩展的概念。它定义了两个符号和由这两个符号组成的一个简单表达式。最后它打印了这个表达式及其扩展形式：

  1. import sympy
  2. a = sympy.Symbol('a')
  3. b = sympy.Symbol('b')
  4. e = (a + b) ** 4
  5. print e
  6. print e.expand()

输出结果是：

  1. (a + b)**4
  2. a**4 + 4*a**3*b + 6*a**2*b**2 + 4*a*b**3 + b**4

3. 表达式或公式的简化

SymPy可以很便利地简化数学表达式。下面的程序简化了两个表达式，然后显示了简化后的表达式结果：

  1. import sympy
  2. x = sympy.Symbol('x')
  3. a = 1/x + (x*exp(x) - 1)/x
  4. simplify(a)
  5. simplify((x ** 3 + x ** 2 - x - 1)/(x ** 2 + 2 * x + 1))

输出结果是：

  1. ex
  2. x – 1

4. 单的积分

下面的程序计算了两个简单函数的积分：

  1. import sympy
  2. from sympy import integrate
  3. x = sympy.Symbol('x')
  4. integrate(x ** 3 + 2  x  2 + x, x)
  5. integrate(x / (x * 2 + 2 * x), x)

输出结果是：

  1. x**4/4+2x*3/3+x**2/2
  2. log(x + 2)

4.3　数据分析和可视化的API和工具

Python中有很优秀的工具和API可以用来分析、可视化和展示数据和计算的结果。在以下的讨论中将介绍pandas的概念和操作。我们会用示例程序简单地讨论matplotlib的图表绘画并导出成不同格式。可以将图表导出成图片文件或PDF等其他文件。在第7章中将详细讨论matplotlib和pandas以及IPython工具的概念。

4.3.1　用pandas进行数据分析和操作

pandas是一个用于数据分析和数据操作的工具包。pandas由一些数据结构组成，这些数据结构在Python中用于科学数据分析。pandas开发的终极目标是设计一个强大和灵活的数据操作和分析工具。它提供了有效、灵活和意义重大的数据结构，特殊的设计使得它能够处理任意种类的数据。pandas可以用于大部分常用的数据库和数据集。pandas是在NumPy的基础上开发的。

因此它支持与Python其他的科学计算API和工具进行整合。pandas可以用于以下所有类型的数据。

  • 表格数据，例如关系型数据库或电子表格（如微软Excel）。

  • 有序或无序的时间序列数据。

  • 多维阵列数据，例如带有行和列标签的矩阵。

  • 用于存储第3章中提到的任意格式的科学数据的任意数据集。

1. pandas的重要数据结构

pandas数据结构的范围可以从一维到三维。Series是一维的，DataFrame是二维的，Panel是三维甚至更高维的数据结构。高维（如四维）数据结构目前仍然在开发中。通常，Series和DataFrame可以用于大多数统计、工程、财务和社会科学的场景中。

  • Series：它是一个带标签的一维数组，可以用于存储任意数据类型，例如整型、浮点数、字符串和其他有效的Python对象。它的轴的标签也称作index。

  • DataFrame：它是一个带标签的二维数组，有行和列。列可以有多种类型。DataFrame可以看作类似二维结构，例如电子表格和数据库表格。DataFrame也可以看作包含多个不同类型的Series的集合。

  • Panel：在统计学和经济学中，面板数据（panel data）指多维数据，这个多维数据包括不同时间的不同测量结果。该数据结构的名称来源于其概念。与Series和DataFrame相比，面板数据是不太常用的一种数据结构。

2. pandas的特点

下面是pandas的一些突出特性。

  • 它提供了针对pandas数据结构以及CSV、微软Excel、SQL数据库和HDF5等数据格式的数据的操作便利性。

  • 它被高度地优化以获得高性能，其关键代码是用Cython和C开发的。

  • 它支持用切片、索引和子集进行大数据集的分割。

  • 它提供自动和简洁的数据对齐。通过用标签集合简洁地将对象进行对齐。如果用户忽略标签，那么数据结构会自动对齐数据。

  • 数据结构支持大小动态变化，因为列可以被插入或删除。

  • pandas拥有强大的group by操作引擎，group by操作用于数据的聚合和变换。

  • 它还支持用于数据整合的高效的合并和连接操作。

  • 它还用到重新索引以管理缺失数据的概念。缺失数据是指空的或不存在的数据。

  • pandas还对时间序列功能有很好的支持。这些功能包括移动窗口统计信息、日期范围的生成和频率转换、日期移位和延迟、移动时间窗口线性回归等。

4.3.2　用matplotlib进行数据可视化

matplotlib是用于数据可视化的Python API，是最广泛使用的二维图像Python包。它提供了一个快速可定制的数据可视化方法，并实现不同格式图片的发布。它支持多维图表的绘画。matplotlib中规定了图表的大多数属性的默认值，但这些值是可以定制的。用户可以控制任意图表的几乎所有设置，例如图的大小、线的宽度、颜色和类型、坐标轴、点的属性、文本的属性（例如字体、字面和字号）。

我们来讨论一些示例。示例中用到不同格式的绘画和不同格式的导出。

4.3.3　用IPython实现Python的交互式计算

Python有两种流行的编程方式：交互式编程与脚本文件。一些程序员比较喜欢与脚本打交道。通常他们用一个文本编辑器来写自己的程序，用终端来执行或进行其他操作，例如程序调试。然而，科学计算应用通常需要一个良好的交互式计算环境。在交互式计算中，任何时候计算环境都可以处理人们输入的内容，可能来自命令行或图像用户界面。Python科学计算API通过IPython及与其绑定的工具集合获得一个交互式计算环境。IPython广泛用于各种科学计算应用中，例如数据管理、数据操作、数据分析、数据可视化、科学计算和大规模计算。

我们来讨论在IPython中用NumPy、SymPy、pandas和matplotlib进行计算的一些例子。

4.3.4　数据分析和可视化的示例程序

这一小节将讨论用matplotlib和pandas进行数据分析和可视化的示例程序。如果你没有本地安装的pandas和matplotlib，可以用在线的IPython，网址是https://www.pythonanywhere.com/try-ipython/。

首先需要一些用于分析或可视化的数据。下面的程序从雅虎财经获取了苹果公司从2014年10月1日至2015年1月31日的数据，并将该数据存储在一个CSV文件中：

  1. import pandas as pd
  2. import datetime
  3. import pandas.io.data
  5. start = datetime.datetime(2014, 10, 1)
  6. end = datetime.datetime(2015, 1, 31)
  8. apple = pd.io.data.get_data_yahoo('AAPL', start, end)
  9. print(apple.head())
  10. apple.to_csv('apple-data.csv')
  11. df = pd.read_csv('apple-data.csv', index_col='Date', parse_dates=True)
  12. df.head()

以下是输出。

Open High Low Close Volume Adj close
Date
10/1/2014 100.59 100.69 98.7 99.18 51491300 98.36
10/2/2014 99.27 100.22 98.04 99.9 47757800 99.08
10/3/2014 99.44 100.21 99.04 99.62 43469600 98.8
10/6/2014 99.95 100.65 99.42 99.62 37051200 98.8
10/7/2014 99.43 100.12 98.73 98.75 42094200 97.94

下面的程序对前面例子中的.csv文件中的数据进行画图。它计算了close的50个移动平均值（50 MA）。然后在二维图像中画出open、close、high、low和50个移动平均值。下面的截图是程序输出的图像。

{%}

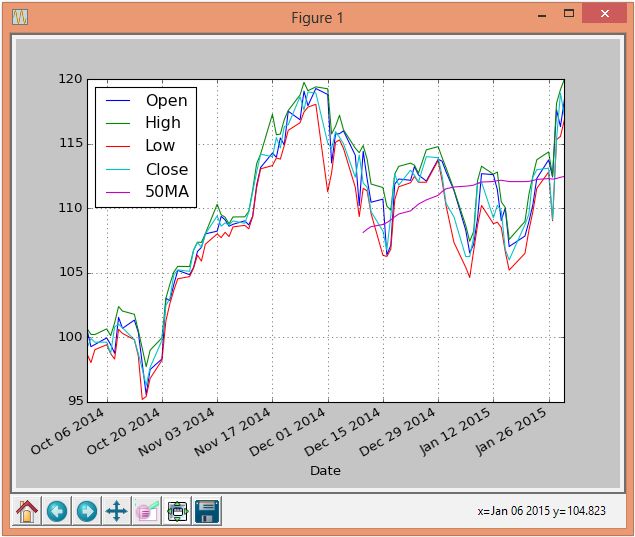
下面是程序：

  1. import pandas as pd
  2. import matplotlib.pyplot as plt
  4. df = pd.read_csv('apple-data.csv', index_col = 'Date', parse_
  5. dates=True)
  6. df['H-L'] = df.High - df.Low
  7. df['50MA'] = pd.rolling_mean(df['Close'], 50)
  8. df[['Open','High','Low','Close','50MA']].plot()
  9. plt.show()

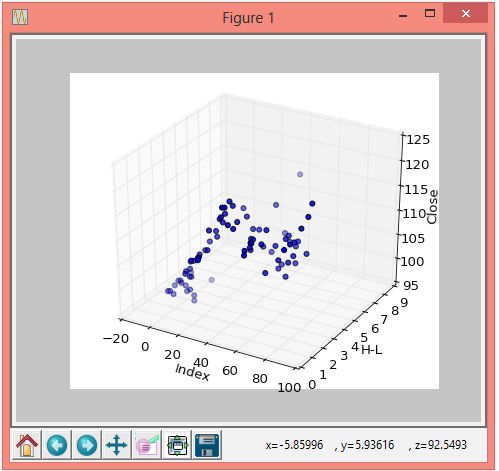
现在下面的程序对同样的数据进行了三维绘图：

  1. import pandas as pd
  2. import matplotlib.pyplot as plt
  3. from mpl_toolkits.mplot3d import Axes3D
  5. df = pd.read_csv('apple-data.csv', parse_dates=True)
  6. print(df.head())
  7. df['H-L'] = df.High - df.Low
  8. df['50MA'] = pd.rolling_mean(df['Close'], 50)
  10. threedee = plt.figure().gca(projection='3d')
  11. threedee.scatter(df.index, df['H-L'], df['Close'])
  12. threedee.set_xlabel('Index')
  13. threedee.set_ylabel('H-L')
  14. threedee.set_zlabel('Close')
  15. plt.show()
  17. threedee = plt.figure().gca(projection='3d')
  18. threedee.scatter(df.index, df['H-L'], df['Volume'])
  19. threedee.set_xlabel('Index')
  20. threedee.set_ylabel('H-L')
  21. threedee.set_zlabel('Volume')
  22. plt.show()

前面的程序的三维绘图的截图如下所示。

{%}

4.4　小结

这一章讨论了各种科学计算API和工具的概念、特点和一些示例程序。首先讨论了NumPy和SciPy。在介绍了NumPy后，讨论了与符号计算相关的概念和SymPy。

之后，讨论了交互式计算、数据分析和数据可视化的API和工具。IPython是交互计算的Python工具。还讨论了数据分析包pandas和数据可视化API matplotlib。

在下一章，我们将详细讨论数值计算API——NumPy。还会通过示例程序介绍NumPy的各种函数和相关的数学概念。