第 5 章 数值计算
本章将通过程序示例讨论NumPy和SciPy的大部分功能。首先通过举例详细地讨论NumPy和SciPy中的数组和运算。这会为学习NumPy和SciPy的各种高级功能打下坚实的基础。
这一章将谈论以下主题:
用NumPy和SciPy做科学数值计算
NumPy的基本对象
NumPy的各种包/模块
SciPy包的基础知识
SciPy的数学函数
高级数学模块和包
在Python中,NumPy是数值计算的基础,其最基本和最重要的创意是支持多维数组。我们首先讨论NumPy中数组的基本概念。在了解了基础知识之后,再讨论可以对多维数组进行的各种运算。还会讨论到NumPy支持的各种基础的和高级的数学函数。NumPy包含一些子包或子模块,可以支持高级数学计算。
5.1 NumPy的基本对象
NumPy和SciPy的所有科学计算功能建立在NumPy两种基本类型的对象之上。第一种对象是 N 维数组对象,即ndarray;第二种对象是通用函数对象,即ufunc。除了这两种对象,还有其他一些对象建立在它们之上。
5.1.1 N 维数组对象
ndarray对象是一个同质元素的集合,这些元素用 N 个整型数索引(N 是数组的维数)。ndarray有两个重要的属性。第一个属性是数组中元素的数据类型,称作dtype;第二个属性是数组的维度。数组的数据类型可以是Python支持的任意数据类型。数组的维度是一个元组(N-tuple),即一个包含 N 维数组的 N 个元素的集合,元组中的每个元素定义了数组在该维度包含的元素个数。
1. 数组的属性
除了维度和dtype,数组还有其他属性,列举如下:
大小(
size)每项的大小(
itemsize)数据(
data)维度(
ndim)
每项的大小(itemsize)是数组中每个元素的字节长度。数据(data)属性是一个Python缓存对象,该对象指向数组数据的起始位置。可通过以下的Python程序来理解维度、数据类型和其他属性的概念:
import numpy as npx2d = np.array( ( (100,200,300),(111,222,333),(123,456,789) ) )x2d.shapex2d.dtypex2d.sizex2d.itemsizex2d.ndimx2d.data
2. 数组的基本操作
使用方括号([])来索引数组的值称作数组索引(array indexing)。以上面的程序中定义和用到的二维数组x2d为例,该数组中的特定元素可以用x2d[row, column]表示。例如,x2d[1,1]表示第二行的第二个元素(即222),索引值的起始值是0。同样,x2d[2,1]表示第三行的第二个元素(即456)。
数组切片是从数组中选定某些元素来构成一个子数组的过程。对于一维数组,我们可以依次从数组中选择某些元素。进而可以通过切片获取二维数组的一整行或一整列。也就是说我们可以在任一维度选取数组元素。Python的基本切片概念被扩展到了 N 维数组中。切片的基本语法是start:stop:step。第一个参数指切片的起始位置索引值,第二个参数是指切片结束位置的索引值,最后一个参数定义了相加于前一个选定元素索引值基础上的步长。如果我们省略前两个参数值中的任意一个,那么这个值会被默认当作零或者大于零。同样,步长的默认值是1。下面用几个例子来更清楚地理解切片。
以x2d这个6×3的数组为例。x2d[1]等价于x2d[1, :],都表示数组的第二行,该行包含三个元素。另一方面,x2d[:, 1]表示数组的第二列,该列包含六个元素。x2d[::3,1]可以选中数组中第二列的每三个元素。
省略号可以用来替换零个或多个冒号。一个省略号可以当作零个或多个全切片的对象,以匹配切片对象的所有维度,这个维度必须和原始数组的维度相等。例如,如果x4d是一个5×6×7×8的数组,那么x4d[2 :, …, 6]等价于x4d[2 :, :, :, 6]。同样,x4d[…, 4]等价于x4d[:, :, :, 4]。可用以下程序理清数组切片的概念。这个程序展示了一维数组和二维数组的切片:
import numpy as npx = np.array([1,12, 25, 8, 15, 35, 50, 7, 2, 10])x[3:7]x[1:9:2]x[0:9:3]x2d = np.array(( (100,200,300),(111,222,333),(123,456,789),(125,457,791),(127,459,793),(129,461,795) ))x2d[0:4,0:3]x2d[0:4:2,0:3:2]
数组的迭代可以用for循环实现。在一维数组中,可以用for循环连续地获得所有元素。另一方面,多维数组的迭代可以通过考虑到第一维数据的多重循环来实现。下面的程序展示了如何实现数组的迭代:
import numpy as npx = np.array([1,12, 25, 8, 15, 35, 50, 7, 2, 10])x2d = np.array(( (100,200,300),(111,222,333),(123,456,789),(125,457,791),(127,459,793),(129,461,795) ))for i in x:print ifor row in x2d:print row
3. 数组的特殊操作(变形及转换)
为了实现数组的变形,有ravel、reshape、resize和指定数组维度属性等方法。ravel和reshape方法返回修改了维度的变量(被调用的对象),而resize和指定数组维度属性的办法则修改了实际数组的维度。ravel方法将数组展开成C语言类型的数组,它返回的变量被当作一个一维数组,这个数组按行依次展开成一个一维数组。
我们用下面的程序来讨论这些方法的影响。这个程序实现了二维数组的变形操作。第一个print函数输出的是原始数组。ravel函数将展示展开的数组。而ravel函数之后的print函数再次展示了原始数组,因为ravel函数并未改变原始数组。现在uresize函数将原始的6行3列的数组(6,3)变形为3行6列的数组(3,6)。因此resize之后的print函数将输出变形之后的数组形状。
现在我们对原始数组(6,3)应用了reshape函数。但是由于reshape不改变原始数组的形状,在reshape函数之后的print函数将会打印出(3,6)的数组。最后一种方法是指定数组的形状为(9,2),将数组的形状变成(9,2)。
最重要的是要记住,当做reshape变换时,新数组的总大小仍然不变:
import numpy as npx2d = np.array(( (100,200,300),(111,222,333),(123,456,789),(125,457,791),(127,459,793),(129,461,795) ))print x2dx2d.ravel()print x2dx2d.resize((3,6))print x2dx2d.reshape(6,3)print x2dx2d.shape = (9,2)print x2d
如果需要的话,tolist、tofile和tostring可以分别将数组转换为Python列表数据结构、存储的文件和字符串。
4. 与数组相关的类
有一些类和子类是和ndarray类相关的。这些类的目的是为了支持特定的增强功能。下面将讨论这些类和子类。
(1) 矩阵子类
matrix类是ndarray的Python子类。一个矩阵能够通过其他矩阵或字符串生成,或者通过其他可以转化为ndarray的对象生成。matrix子类拥有特殊的覆盖运算符,例如*是矩阵的乘,**是矩阵的幂运算。matrix类提供的一些函数可以实现多种功能,例如元素排序、转置计算、矩阵元素的求和、将矩阵转换为列表或者其他数据结构和数据类型。下面的程序定义了两个3行3列的矩阵。最后程序输出了两个矩阵的乘积:
import numpy as npa = np.matrix('1 2 3; 4 5 6; 7 8 9')print ab = np.matrix('4 5 6; 7 8 9; 10 11 12')print bprint a*b
(2) 掩码数组
NumPy有一个生成掩码数组的模块numpy.ma。掩码数组是一个包含一些非法的、缺失的、未预料的实体的正常数组。掩码数组有两个组成成分:原始ndarray和一个掩码。掩码是由布尔逻辑值组成的数组,可以用来判定数组的值是有效还是无效。掩码中的一个true值反应了数组里相应的值是无效的。在掩码数组后面的计算中,这些无效的实体将不会用到。下一个程序展示了掩码数组的概念。假设原始数组x里包含不同人的脉搏率,并且其中有两个非法实体。为了掩盖这两个非法实体,掩码中相应的值被设置成1(true)。最后我们计算原始数组和掩码数组的平均值。没用掩码处理的平均值是61.1,因为包含两个负值,而用掩码进行处理后的平均值是94.5:
import numpy as npimport numpy.ma as max = np.array([72, 79, 85, 90, 150, -135, 120, -10, 60, 100])mx = ma.masked_array(x, mask=[0, 0, 0, 0, 0, 1, 0, 1, 0, 0])mx2 = ma.masked_array(x,mask=x<0)x.mean()mx.mean()mx2.mean()
(3) 结构化的数组
NumPy的ndarray能包含记录类型的值。为了生成一个记录类型的数组,首先需要生成记录类型的数据类型,然后用这种数据类型的元素构建数组。这种数据类型可以通过dtype在数组定义中定义。下面的程序中生成了一个记录类型的数组,这个数组中包含城市的最低、最高和平均气温。dtype函数由两部分组成:域的命名和格式。例子中用到的格式是32位整型(i4)、32位浮点型(f4)和包含30或更少的字符的字符串(a30):
import numpy as nprectype= np.dtype({'names':['mintemp', 'maxtemp', 'avgtemp', 'city'], 'formats':['i4','i4', 'f4', 'a30']})a = np.array([(10, 44, 25.2, 'Indore'),(10, 42, 25.2, 'Mumbai'), (2,48, 30, 'Delhi')],dtype=rectype)print a[0]print a['mintemp']print a['maxtemp']print a['avgtemp']print a['city']
5.1.2 通用函数对象
通用函数(unfunc)是对ndarray进行一个元素一个元素操作的函数。它也支持广播、类型转换和一些其他重要的特征。在NumPy中,广播是对不同维度数组的操作过程。特别是在数学运算中,较小维度的数组要在大维度的数组中广播,以使其维度和大维度数组兼容。通用函数即是NumPy中ufunc类的实例。
1. 属性
每个通用函数都有一些属性,但是用户无法设置这些属性的值。下面是通用函数的属性,这是一些通用函数的信息属性。
__doc__:它包含了ufunc函数的doc字符串。其第一部分是基于命名、输入的数量和输出的数量动态生成的。第二部分是在函数生成时定义的,并存在函数中。__name__:这是ufunc的命名。ufunc.nin:这表示总的输入数量。ufunc.nout:这表示总的输出数量。ufunc.nargs:这表示总的变量数,包括输入和输出的数量。ufunc.ntypes:这表示这个函数定义的类型的种类。ufunc.types:这个属性返回函数定义的ntypes种具体类型的列表。ufunc.identity:这表示这个函数的值。
2. 方法
所有的通用函数ufunc有5种方法,如下所示。前4种方法的通用函数包含两个输入变量,返回一个输出变量。这些方法在调用其他函数失败时会报出ValueError异常。第五种方法允许用户利用索引做位置操作。下面是每个NumPy通用函数可用的方法。
ufunc.reduce:在一个坐标轴应用通用函数时,它可以将数组降低一个维度。ufunc.accumulate:它可以在对所有元素使用同一个运算符时积累结果。ufunc.reduceat:它可以在单个坐标轴上减少指定的切片。ufunc.outer(A, B):它对所有(a, b)应用通用函数操作符,其中a包含于A,b包含于B。ufunc.at:它对特定元素执行未缓存的位置操作。
3. 各种可用的通用函数
目前NumPy支持超过60种的通用函数。这些函数包括广泛的操作,如简单的数学运算(加、减、求模、取绝对值)、开方、幂运算、指数运算、三角运算、比特位运算、比较和浮点运算。通常最好选择利用这些函数而不选择循环,因为相比于循环这些函数更高效。
下面的程序展示了一些通用函数的运用:
import numpy as npx1 = np.array([72, 79, 85, 90, 150, -135, 120, -10, 60, 100])x2 = np.array([72, 79, 85, 90, 150, -135, 120, -10, 60, 100])x_angle = np.array([30, 60, 90, 120, 150, 180])x_sqr = np.array([9, 16, 25, 225, 400, 625])x_bit = np.array([2, 4, 8, 16, 32, 64])np.greater_equal(x1,x2)np.mod(x1,x2)np.exp(x1)np.reciprocal(x1)np.negative(x1)np.isreal(x1)np.isnan(np.log10(x1))np.sqrt(np.square(x_sqr))np.sin(x_angle*np.pi/180)np.tan(x_angle*np.pi/180)np.right_shift(x_bit,1)np.left_shift (x_bit,1)
在Python中,如果有一个值不能用数字表示,那么这个值就是空值nan。例如,如果对前一个程序中的x1数组做log10的通用函数运算,那么输出值就是nan。有一个通用函数isnan可用来检验一个值是不是nan。三角函数需要角度值度数的变量。十进制常数值是弧度值,可以通过乘以180/numpy.pi来实现度数的转换。比特位左移1位执行的是变量乘以2。类似地,比特位右移1位执行的是变量除以2。通常,这些通用函数都是对数组进行操作,如果有非数组的变量的话,那么这个变量通过广播机制当作一个数组,然后执行逐元素的操作。这就是前一个程序中最后四行的操作。
5.1.3 NumPy的数学模块
NumPy加入了特定功能的模块,例如线性代数、离散傅里叶变换、随机采样和矩阵代数库。这些功能捆绑在单独的模块中,这些模块列举如下。
numpy.linalg:这个模块支持线性代数的各种功能,如数组和向量的内积、外积和点积;向量和矩阵的范数;线性矩阵方程的解;矩阵转置的方法。
numpy.fft:离散傅里叶变换在数字信号处理中有广泛的应用。这个模块中的函数可以计算各种类型的离散傅里叶变换,包括一维、二维、多维、转置和傅里叶变换。
numpy.matlib:这个模块包括那些默认返回矩阵对象而不是ndarray对象的函数。这些函数包括
empty、zeros、ones、eye、rapmat、rand、randn、bmat、mat和matrix。numpy.random:这个模块包括在特定人群或范围中执行随机抽样的函数。它也支持随机排列组合的生成。另外,它还包括一些支持各种基于统计分布生成的随机抽样数值的函数。
下面一个程序展示了linalg模块中的一些函数的应用。它计算了范数、转置、行列式、特征值和方阵右特征向量。它还通过求解两个方程2x+3y=4和3x+4y=5展示了线性方程的求解,并且是通过将它们当作数组来求解的。最后一行的allclose函数比较了传入的两个数组,并且当它们的每个元素都相等时返回true。eig方法计算了方阵的特征值和特征向量。返回值如下:w是特征值,v是特征向量,v[:,i]列是w[i]的特征向量。
import numpy as npfrom numpy import linalg as LAarr2d = np.array(( (100,200,300),(111,222,333),(129,461,795) ))eig_val, eig_vec = LA.eig(arr2d)LA.norm(arr2d)LA.det(arr2d)LA.inv(arr2d)arr1 = np.array([[2,3], [3,4]])arr2 = np.array([4,5])results = np.linalg.solve(arr1, arr2)print resultsnp.allclose(np.dot(arr1, results), arr2)
随机抽样是科学和商业计算中很重要的方面。下面的程序展示了numpy随机抽样模块支持的各类函数中的部分函数。除了样本维度与总体,有些分布还需要一些统计值,例如均值、众数、标准差。permutation函数随机排列一个序列或者返回一个排列范围,randint函数随机返回最初的两个变量所指定的范围中的一些元素,而元素的总个数由第三个变量指定。剩余的方法返回特定分布中的抽样,如卡方检验、帕雷托分布、正态分布和对数正态分布。
import numpy as npnp.random.permutation(10)np.random.randint(20,50, size=10)np.random.random_sample(10)np.random.chisquare(5,10) # 自由度alpha, location_param = 4., 2.s = np.random.pareto(alpha, 10) + location_params = np.random.standard_normal(20)mean, std_deviation = 4., 2.s = np.random.lognormal(mean, std_deviation, 10)
5.2 SciPy的介绍
SciPy包含一系列子模块,专用于各种科学计算的应用。SciPy社区建议,科学家们在补充某个函数进SciPy前,首先应检查该函数是否已经包括在SciPy中。因为几乎所有科学计算的基本函数已经在SciPy中实现完成,所以检查可以省去科学家们重新编写该函数的精力。并且,SciPy模块已经被优化并且经过了良好的缺陷和可能的错误测试。因此,利用SciPy可以获得很好的性能。
5.2.1 SciPy的数学函数
SciPy是写于NumPy之上的,扩展了NumPy的功能以执行高级的数学功能。NumPy中可用的基础的数学函数没有被重新设计以执行这些功能。我们还需要用到NumPy的函数,在本章随后的程序中将看到其应用。
5.2.2 高级模块/程序包
SciPy的功能被分成一些独立的任务特定的模块。我们将逐个讨论这些模块。为简洁起见,将不会谈到任一模块的所有函数,而是给出SciPy中每个模块的一些示例。
1. 积分
scipy.integrate子包中有几个用到不同积分方法的积分函数,包括对常微分方程的积分。当函数对象给定时,可以用几种积分函数。当固定样本给定时,也有几种积分函数。
下面是给定函数对象的积分函数。
quad:通用积分dblquad:通用二重积分tplquad:通用三重积分nquad:通用 N 重积分fixed_quad:对func(x)做 N 维高斯积分quadrature:在给定容限范围内的高斯积分romberg:对函数做Romberg积分
下面是固定样本给定时的积分函数。
cumtrapz:用梯形积分法计算积分simps:用辛氏法则从样本中计算积分romb:用Romberg积分法从(2**k + 1)个均匀间隔的样本中计算积分
下面是用于常微分方程中的积分函数。
odeint:差分方程的通用积分ode:用VODE和ZVODE的方式进行ODE积分complex_ode:将复数值的ODE转化成实数并积分
来讨论上述列表中列举的函数。quad函数执行函数的通用积分,积分范围在负无穷大到正无穷大之间。在下面的程序中,用这个函数计算第一类贝赛尔函数在(0,20)区间的积分。第一类贝赛尔函数在special.jv中做了定义。下面程序的最后一行用quad函数计算了高斯积分:
import numpy as npfrom scipy import specialfrom scipy import integrateresult = integrate.quad(lambda x: special.jv(4,x), 0, 20)print resultprint "Gaussian integral", np.sqrt(np.pi),quad(lambda x: np.exp(-x**2),-np.inf, np.inf)
如果函数在积分时需要额外的参数,例如变量进行乘或乘方的因子,那么这些参数就可以作为变量传入。下面的程序展示了将a、b和c作为变量传入quad函数。有时积分会慢慢地发散或收敛:
import numpy as npfrom scipy.integrate import quaddef integrand(x, a, b, c):return axx+b*x+ca = 3b = 4c = 1result = quad(integrand, 0,np.inf, args=(a,b,c))print result
二重积分和三重积分可以用dblquad和tplquad函数来实现。下面的程序示范了dblquad函数的应用。变量t和x的变化范围从0到无穷(inf)。注释后面的代码在指定的区间做了高斯积分:
import numpy as npfrom scipy.integrate import quad, dblquad, fixed_quaddef integrand1 (t, x, n):return np.exp(-x*t) / t**nn = 4result = dblquad(lambda t, x: integrand1(t, x, n), 0, np.inf, lambdax: 0, lambda x: np.inf)# 下面代码实现固定间隔的高斯积分from scipy.integrate import fixed_quad, quadraturedef integrand(x, a, b):return a * x + ba = 2b = 1fixed_result = fixed_quad(integrand, 0, 1, args=(a,b))result = quadrature(integrand, 0, 1, args=(a,b))
对于带有任意间隔采样的函数的积分,可以用simps函数。辛普森法则可以估计三个相邻点间的函数为抛物线函数。下面的程序演示了simps函数:
import numpy as npfrom scipy.integrate import simpsdef func1(a,x):return ax*2+2def func2(b,x):return bx*3+4x = np.array([1, 2, 4, 5, 6])y1 = func1(2,x)Intgrl1 = simps(y1, x)print(Intgrl1)y2 = func2(3,x)Intgrl2 = simps (y2,x)print (Intgrl2)
下面的程序用odeint函数做常微分方程的积分:
import matplotlib.pyplot as pltfrom numpy import linspace, arraydef derivative(x,time):a = -2.0b = -0.1return array([ x[1], a*x[0]+b*x[1] ])time = linspace (1.0,15.0,1000)xinitialize = array ([1.05,10.2])x = odeint(derivative,xinitialize,time)plt.figure()plt.plot(time,x[:,0])plt.xlabel('t')plt.ylabel('x')plt.show()
2. 信号处理(scipy.signal)
信号处理工具箱包含一系列滤波函数、滤波器设计函数,以及对一维和二维数据进行B—样条插值的函数。这个工具箱包含的函数可以进行以下操作:
卷积
B—样条
滤波
滤波器设计
Matlab式的IIR滤波器设计
连续时间的线性系统
离散时间的线性系统
线性时不变系统
信号波形
窗函数
小波分析
谱峰的找寻
光谱分析
可通过一些示例程序来理解信号处理工具箱的功能。
detrend函数是一个滤波函数。该函数从数据中沿着坐标轴去除常量或线性趋势,使得我们可以看到高阶的效果。具体程序如下所示:
import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltfrom scipy import signalt = np.linspace(0, 5, 100)x = t + np.random.normal(size=100)plt.plot(t, x, linewidth=3)plt.show()plt.plot(t, signal.detrend(x), linewidth=3)plt.show()
下面的程序应用样条滤波来处理“Lena的脸”图像边缘,用misc.lena命令将这张图片数据当作一个数组。用两个函数实现滤波功能。首先,cspline2d命令将一个带有镜像对称边界的二维FIR滤波器应用于样条系数。这个函数比convolve2d函数快,convolve2d函数对任意二维滤波器卷积并允许你选择镜像对称边界:
import numpy as npfrom scipy import signal, miscimport matplotlib.pyplot as pltimg = misc.lena()splineresult = signal.cspline2d(img, 2.0)arr1 = np.array([[-1,0,1], [-2,0,2], [-1,0,1]], dtype=np.float32)derivative = signal.convolve2d(splineresult,arr1,boundary='symm',mode='same')plt.figure()plt.imshow(derivative)plt.title('Image filtered by spline edge filter')plt.gray()plt.show()
3. 傅里叶变换(scipy.fftpack)
对实数或复数序列的离散傅里叶变换和离散傅里叶逆变换可以分别用fft和ifft函数来计算,fft是指快速傅里叶变换。下面的程序是一个示例:
import numpy as npfrom scipy.fftpack import fft, ifftx = np.random.random_sample(5)y = fft(x)print yyinv = ifft(y)print yinv
下面的程序画出了三个正弦函数的和的FFT:
import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltfrom scipy.fftpack import fftx = np.linspace(0.0, 1, 500)y = np.sin(100*np.pi*x) + 0.5*np.sin(150*np.pi*x) + 0.75*np.sin(200*np.pi*x)yf = fft(y)xf = np.linspace(0.0, 0.1, 250)import matplotlib.pyplot as pltplt.plot(xf, 2.0/500 * np.abs(yf[0:500/2]))plt.grid()plt.show()
4. 空间数据结构和算法(scipy.spatial)
空间分析是一系列用于分析空间数据的技巧和算法。空间数据是指和地理空间或垂直空间相关的数据对象或元素。这种数据包括点、线、多边形、其他几何和地理特征信息,几何和地理特征信息可以映射为位置信息,用于跟踪或定位各种装置。这种提供地理或空间位置信息的数据可能是标量或是矢量的。空间数据被用于各种领域的各种应用,如地理学、地理信息系统/检索、基于位置的服务、基于网页和基于桌面的空间应用、空间挖掘,等等。
KD树(k-dimensional tree,k-d tree)是一种空间划分数据结构。它将所有点构建在k维空间中。在数学上,空间划分是将一个空间划分为多个相邻空间的过程。它将空间分成不重叠的区域,空间中的每个点只属于一个区域。
SciPy拥有支持各种空间计算功能的模块。用户可以计算Delaunay三角剖分、Voronoi图、N维凸包。SciPy还有画图工具,可以将这些计算结果画在二维空间中。此外,SciPy还支持KDTree功能(scipy.spatial.KDTree)实现快速近邻查找算法,还可以对初始向量集合进行距离矩阵的计算。
通过一些示例程序来看这些函数。下面的程序做了Delaunay三角剖分,并将计算结果用pyplot画出:
import numpy as npimport matplotlib.pyplot as pltfrom scipy.spatial import Delaunayarr_pt = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])arr1 = np.array([0., 0., 1., 1.])arr2 = np.array([0., 1.1, 0., 1.])triangle_result = Delaunay(arr_pt)plt.triplot(arr1, arr2, triangle_result.simplices.copy())plt.show()plt.plot(arr1, arr2, 'ro')plt.show()
最小的凸的对象包括给定点集合中的所有点,该对象被称作凸包,它可以用convexHull函数来计算。下面的程序展示了convexHull这个函数的应用,并将计算结果画出:
import numpy as npfrom scipy.spatial import ConvexHullimport matplotlib.pyplot as pltrandpoints = np.random.rand(25, 2)hull = ConvexHull(randpoints)# 下面一行代码画图plt.plot(randpoints[:,0], randpoints[:,1], 'x')# 通过for循环画出各个线段for simplex in hull.simplices:plt.plot(randpoints[simplex,0], randpoints[simplex,1], 'k')plt.show()
可以用KDTree来查找点集中离选定点最近的点。下面的程序展示了KD树的应用:
from scipy import spatialx_val, y_val = np.mgrid[1:5, 3:9]tree_create = spatial.KDTree(zip(x_val.ravel(), y_val.ravel()))tree_create.datapoints_for_query = np.array([[0, 0], [2.1, 2.9]])tree_create.query(points_for_query)
下面的程序显示了最近的距离和索引值:
import numpy as npimport matplotlib.pyplot as pltfrom scipy.spatial import KDTreevertx = np.array([[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3,1], [3, 2], [3, 3]])tree_create = KDTree(vertx)tree_create.query([1.1, 1.1])x_vals = np.linspace(0.5, 3.5, 31)y_vals = np.linspace(0.5, 3.5, 33)xgrid, ygrid = np.meshgrid(x, y)xy = np.c_[xgrid.ravel(), ygrid.ravel()]plt.pcolor(x_vals, y_vals, tree.query(xy)[1].reshape(33, 31))plt.plot(points[:,0], points[:,1], 'ko')plt.show()
5. 最优化(scipy.optimize)
最优化是查找带一个或多个变量的对象函数在多个预先定义变量约束的条件下的最佳方案的过程。对象函数被当作代价函数以最小化,或者被当作利用函数或利益函数以最大化。优化问题有几点重要的事项,例如优化问题的维度和优化的类型。在解决优化问题之前,最好先了解这些事项然后再开始着手解决问题。对于维度的问题,我们指的标量变量的数量是用于寻找最优值的,变量的数量可以是一个或多个。这个变量的数量也会影响最优解的可扩展性。变量的数量越多,求解速度越慢。而且优化类型也会影响解的设计。
另一点需要考虑到的是该问题是否是一个约束问题。所谓约束问题,所指的是最终解必须满足一些预定的约束条件。例如,下面是一个通用约束最小化优化问题的程序:
目标函数: 最小化 f(x)约束条件: gi (x)= ai for i= 1 … … nHj (x)>= bj for j= 1 … … m
最优解必须满足这些约束条件。问题的解取决于目标函数、约束条件和变量间的关系。此外,模型的大小也会影响最优解。模型的大小通过变量的数量和约束条件的数量来确定。通常模型的大小会有一个上限,该上限是优化求解软件或应用强制限定的。这个上限的引入主要是由较高的存储需求、问题的处理需求和数值稳定性决定的。这可能就会导致我们最终找不到最优解,或者求解的过程非常耗时,以致会让人觉得这个解没有收敛。
另外,优化问题可能是凸或非凸的问题。如果是一个凸问题,那么相对来说容易求解,因为它会有一个全局最小或最大值,并且不存在局部最小或最大值。
我们来详细讨论凸度(convexity)的概念。凸优化是在凸集合中最小化convex函数的过程。在某个区间的convex函数(该函数处理实数值)被称作convex函数,条件是图中任意两点间的线段在图中或在图之上。两个常用的convex函数是指数函数(f (x)=ex)和二次函数(f (x)=x2)。凸函数和非凸函数的一些例子如下图所示。
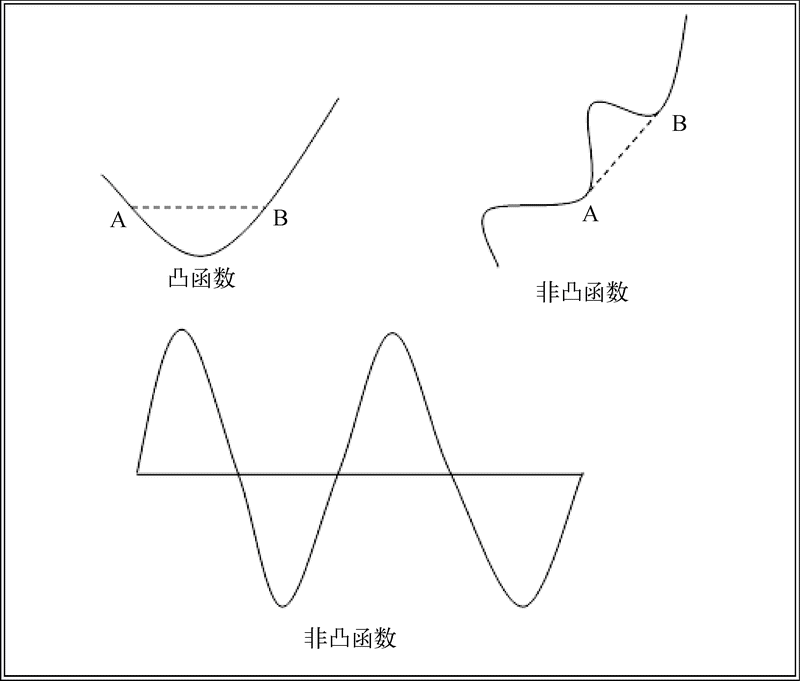
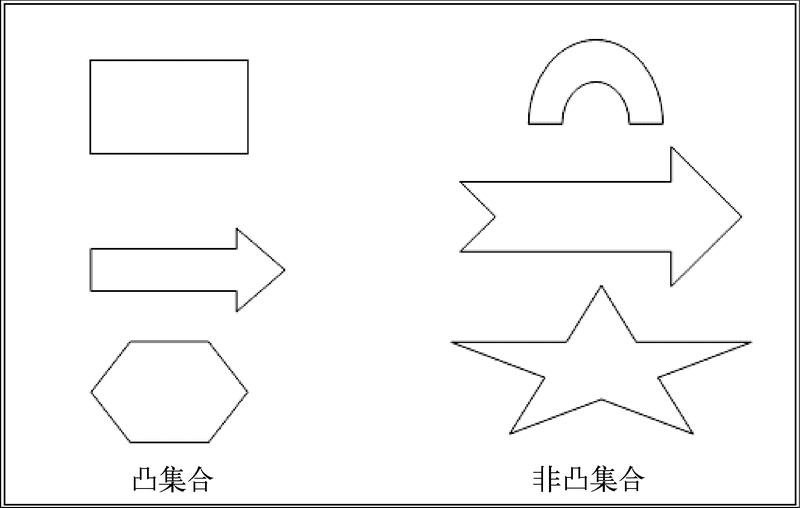
凸集合是指一个区域,该区域中如果我们用线段连接其中的两点,那么线段上的所有点都应该落在该区域中。下图演示了凸集合和非凸集合的区别。
scipy.optimize包提供了标量以及多维函数最小化、曲线拟合和根求解的最有用的函数。来看看如何用这些函数。
下面的程序展示了Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法的运用。这个算法用目标函数的梯度来快速收敛求解。这个程序首先定义了一个叫rosen_derivative的函数来计算rosenbrock函数的梯度:
import numpy as npfrom scipy.optimize import minimizedef rosenbrock(x):return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])def rosen_derivative(x):x1 = x[1:-1]x1_m1 = x[:-2]x1_p1 = x[2:]derivative = np.zeros_like(x)derivative[1:-1] = 200*(x1-x1_m1**2) - 400*(x1_p1 - x1**2)*x1 -\2*(1-x1)derivative[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])derivative[-1] = 200*(x[-1]-x[-2]**2)return derivativeres = minimize(rosenbrock, x0, method='BFGS', jac=rosen_derivative,options={'disp': True})
下面的程序首先计算了Rosenbrock函数的海森矩阵,然后用牛顿共轭梯度法求函数最小值:
import numpy as npfrom scipy.optimize import minimizedef rosenbrock(x):return sum(100.0*(x[1:]-x[:-1]**2.0)**2.0 + (1-x[:-1])**2.0)x0 = np.array([1.3, 0.7, 0.8, 1.9, 1.2])def rosen_derivative(x):x1 = x[1:-1]x1_m1 = x[:-2]x1_p1 = x[2:]derivative = np.zeros_like(x)derivative[1:-1] = 200*(x1-x1_m1**2) - 400*(x1_p1 - x1**2)*x1 - \2*(1-x1)derivative[0] = -400*x[0]*(x[1]-x[0]**2) - 2*(1-x[0])derivative[-1] = 200*(x[-1]-x[-2]**2)return derivativedef rosen_hessian(x):x_val = np.asarray(x)hess = np.diag(-400*x_val[:-1],1) - np.diag(400*x_val[:-1],-1)diagonal = np.zeros_like(x_val)diagonal[0] = 1200*x_val[0]**2-400*x_val[1]+2diagonal[-1] = 200diagonal[1:-1] = 202 + 1200*x_val[1:-1]**2 - 400*x_val[2:]hess = hess + np.diag(diagonal)return hessresult = minimize(rosenbrock, x0, method='Newton-CG', jac=rosen_derivative, hess=rosen_hessian, options={'xtol': 1e-8, 'disp': True})print result.x
minimize函数也有一个对多个约束条件最小化算法的接口。下面的程序用到Sequential Least Square Programming optimization(SLSQP)算法。这个被最小化的函数定义为func,它的导数被定义为func_deriv,约束条件在cons变量中定义:
import numpy as npfrom scipy.optimize import minimizedef func(x, sign=1.0):return sign*(2*x[0]*x[1] + 2*x[0] - x[0]**2 - 2*x[1]**2)def func_deriv(x, sign=1.0):dfdx0 = sign*(-2*x[0] + 2*x[1] + 2)dfdx1 = sign*(2*x[0] - 4*x[1])return np.array([ dfdx0, dfdx1 ])cons = ({'type': 'eq','fun': lambda x: np.array([x[0]**3 - x[1]]),'jac': lambda x: np.array([3.0*(x[0]**2.0), -1.0])},{'type': 'ineq','fun': lambda x: np.array([x[1] - 1]),'jac': lambda x: np.array([0.0, 1.0])})res = minimize(func, [-1.0,1.0], args=(-1.0,), jac=func_deriv,method='SLSQP', options={'disp': True})print(res.x)res = minimize(func, [-1.0,1.0], args=(-1.0,), jac=func_deriv,constraints=cons, method='SLSQP', options={'disp': True})print(res.x)
下面的程序展示了寻找全局最小和局部最小的方法。首先,它定义了一个函数并将其画出。这个函数在-1.3全局最小,在3.8局部最小。BFGF算法用于寻找局部最小。这个程序用BFGF算法寻找全局最小。但是随着网格大小的增加(待检查值的范围),BFGF算法会变慢。所以对于标量函数最好用Brent算法。下面的程序还用到了fminbound函数来寻找0至10区间的局部最小:
import numpy as npimport matplotlib.pyplot as pltfrom scipy import optimizedef f(x):return x**2 + 10*np.sin(x)x = np.arange(-10,10,0.1)plt.plot(x, f(x))plt.show()optimize.fmin_bfgs(f, 0)grid = (-10, 10, 0.1)optimize.brute(f, (grid,))optimize.brent(f)optimize.fminbound(f, 0, 10)
下面的程序展示了约束最优化的应用:
import numpy as npfrom scipy import optimizedef f(x):return np.sqrt((x[0] - 2)**2 + (x[1] - 3)**2)def constraint(x):return np.atleast_1d(2.5 - np.sum(np.abs(x)))optimize.fmin_slsqp(f, np.array([0, 2]), ieqcons=[constraint, ])optimize.fmin_cobyla(f, np.array([3, 4]), cons=constraint)
有多种方法可以求解多项式的根,下面三个程序分别用到了二分法、牛顿—拉斐森法和根函数。下面的程序用二分法求解polynomial_func函数中定义的多项式的根:
import scipy.optimize as optimizeimport numpy as npdef polynomial_func(x):return np.cos(x)**3 + 4 - 2*xprint(optimize.bisect(polynomial_func, 1, 5))
下面的程序用牛顿—拉斐森法求解多项式的根:
import scipy.optimizefrom scipy import optimizedef polynomial_func(xvalue):yvalue = xvalue + 2*scipy.cos(xvalue)return yvaluescipy.optimize.newton(polynomial_func, 1)
在数学上,拉格朗日乘子法被用于寻找函数在等量约束的条件下的局部最小和局部最大。下面的程序用fsolve函数计算了拉格朗日乘子:
import numpy as npfrom scipy.optimize import fsolvedef func_orig(data):xval = data[0]yval = data[1]Multiplier = data[2]return xval + yval + Multiplier (xval*2 + yval**2 - 1)def deriv_func_orig(data):dLambda = np.zeros(len(data))step_size = 1e-3 # 有限微分中使用的步长for i in range(len(data)):ddata = np.zeros(len(data))ddata[i] = step_sizedLambda[i] = (func_orig(data+ddata)-func_orig(data-ddata))/\(2*step_size);return dLambdadata1 = fsolve(deriv_func_orig, [1, 1, 0])print data1, func_orig(data1)data2 = fsolve(deriv_func_orig, [-1, -1, 0])print data2, func_orig(data2)
6. 插值(scipy.interpolate)
插值是在给定的已知的离散值集合范围内寻找新数据点的方法。interpolate子包包含插值运算的各种方法。它支持用spline函数、univariate函数和multivariate函数进行一维和多维插值,拉格朗日和泰勒多项式插值。对于FITPACK和DFITPACK函数,它还有封装类。我们来看上面提到的部分方法的示例程序。
这个程序展示了用线性和立方插值进行的一维插值,并且将插值结果画图进行比较:
import numpy as npfrom scipy.interpolate import interp1dx_val = np.linspace(0, 20, 10)y_val = np.cos(-x**2/8.0)f = interp1d(x_val, y_val)f2 = interp1d(x_val, y_val, kind='cubic')xnew = np.linspace(0, 20, 25)import matplotlib.pyplot as pltplt.plot(x,y,'o',xnew,f(xnew),'-', xnew, f2(xnew),'--')plt.legend(['data', 'linear', 'cubic'], loc='best')plt.show()
下面的程序展示了用griddata函数对超过150个点的多元数据进行插值。点的个数可以调整为合适的值。这个程序用pyplot在一个图像中生成四个子图:
import numpy as npimport matplotlib.pyplot as pltfrom scipy.interpolate import griddatadef func_user(x, y):return x*(1-x)*np.cos(4*np.pi*x) np.sin(4np.piy*2)**2x, y = np.mgrid[0:1:100j, 0:1:200j]points = np.random.rand(150, 2)values = func_user(points[:,0], points[:,1])grid_z0 = griddata(points, values, (x, y), method='nearest')grid_z1 = griddata(points, values, (x, y), method='linear')grid_z2 = griddata(points, values, (x, y), method='cubic')f, axarr = plt.subplots(2, 2)axarr[0, 0].imshow(func(x, y).T, extent=(0,1,0,1), origin='lower')axarr[0, 0].plot(points[:,0], points[:,1], 'k', ms=1)axarr[0, 0].set_title('Original')axarr[0, 1].imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')axarr[0, 1].set_title('Nearest')axarr[1, 0].imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')axarr[1, 0].set_title('Linear')axarr[1, 1].imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')axarr[1, 1].set_title('Cubic')plt.show()
7. 线性代数(scipy.linalg)
SciPy线性代数将变量当作一个对象,这个对象可以转换成一个二维数组并返回一个二维数组。与numpy.linalg相比,scipy.linalg函数有更高级的特征。
下面的程序计算了矩阵(二维数组)的逆。它也用到T(转置的符号)和执行数组的乘法:
import numpy as npfrom scipy import linalgA = np.array([[2,3],[4,5]])linalg.inv(A)B = np.array([[3,8]])A*BA.dot(B.T)
这个小程序计算了矩阵的逆和行列式的值:
import numpy as npfrom scipy import linalgA = np.array([[2,3],[4,5]])linalg.inv(A)linalg.det(A)
下面的程序演示了通过逆矩阵和求解器快速求解线性方程组的方法:
import numpy as npfrom scipy import linalgA = np.array([[2,3],[4,5]])B = np.array([[5],[6]])linalg.inv(A).dot(B)np.linalg.solve(A,B)
下面的程序求解一组线性标量系数并用模型进行数据拟合。这个程序用到linalg.lstsq求解数据拟合问题。lstsq方法被用于寻找线性矩阵方程的最小平方解。这个方法是针对给定数据点寻找最佳拟合线的工具。它使用线性代数和简单的积分:
import numpy as npfrom scipy import linalgimport matplotlib.pyplot as pltcoeff_1, coeff_2 = 5.0, 2.0i = np.r_[1:11] # 也可以用np.arang(1, 11)x = 0.1*iy = coeff_1*np.exp(-x) + coeff_2*xz = y + 0.05 np.max(y) np.random.randn(len(y))A = np.c_[np.exp(-x)[:, np.newaxis], x[:, np.newaxis]]coeff, resid, rank, sigma = linalg.lstsq(A, zi)x2 = np.r_[0.1:1.0:100j]y2 = coeff[0]*np.exp(-x2) + coeff[1]*x2plt.plot(x,z,'x',x2,y2)plt.axis([0,1,3.0,5.5])plt.title('Data fitting with linalg.lstsq')plt.show()
下面的程序展示了用linag.svd和linag.diagsvd函数进行奇异值分解的方法:
import numpy as npfrom scipy import linalgA = np.array([[5,4,2],[4,8,7]])row = 2col = 3U,s,Vh = linalg.svd(A)Sig = linalg.diagsvd(s,row,col)U, Vh = U, Vhprint Uprint Sigprint Vh
8. 用ARPACK解决稀疏特征值问题
下面这个程序计算了标准特征值分解和对应的特征向量:
import numpy as npfrom scipy.linalg import eighfrom scipy.sparse.linalg import eigsh# 限制小数的位数np.set_printoptions(suppress=True)np.random.seed(0)random_matrix = np.random.random((75,75)) - 0.5random_matrix = np.dot(random_matrix, random_matrix.T)# 计算特征值与特征向量eigenvalues_all, eigenvectors_all = eigh(random_matrix)eigenvalues_large, eigenvectors_large = eigsh(random_matrix, 3,which='LM')print eigenvalues_all[-3:]print eigenvalues_largeprint np.dot(eigenvectors_large.T, eigenvectors_all[:,-3:])
如果我们要找最小的特征值,可以用eigenvalues_small, eigenvectors_small = eigsh(random_matrix, 3, which='SM')。在这个例子中系统返回了一个没有收敛的错误。有几种办法可以解决这个问题。第一个办法是通过将tol=1E-2传入eigsh函数增加容限值:eigenvalues_small, eigenvectors_small = eigsh(random_matrix, 3, which='SM', tol=1E-2)。这可以解决问题,但是会损失精度。
另一个解决办法是增加最大的迭代次数至5000,通过将maxiter=5000传入eigsh函数来实现:eigenvalues_small, eigenvectors_small = eigsh(random_matrix, 3, which='SM', maxiter=5000)。但是更多的迭代次数意味着更长的运行时间。还有一个更好的办法来解决快速性和精度问题,那就是用shift-inter模式,用到sigma=0或2和which='LM'参数:eigenvalues_ small, eigenvectors_small = eigsh(random_matrix, 3, sigma=0, which='LM')。
9. 统计学(scipy.stats)
SciPy有很多统计函数可以用于数组的运算,还有用于掩码数组的特殊版本。下面的各个程序展示了部分连续和离散概率分布函数的应用。
下面的程序用到了离散二项式随机变量并画出了它的该概率质量函数。这是一个离散二项分布的概率质量函数:
binom.pmf(k) = choose(n, k) p*k (1-p)*(n-k)
在之前的代码中,k 的取值范围是(0,1,…,n),其中n和p是形状参数:
import numpy as npfrom scipy.stats import binomimport matplotlib.pyplot as pltn, p = 5, 0.4mean, variance, skewness, kurtosis = binom.stats(n, p, moments='mvsk')x_var = np.arange(binom.ppf(0.01, n, p),binom.ppf(0.99, n, p))plt.plot(x_var, binom.pmf(x_var, n, p), 'ro', ms=5, label='PMF of \binomial ')plt.vlines(x_var, 0, binom.pmf(x_var, n, p), colors='r', lw=3,alpha=0.5)plt.show()
下面的程序用到了几何离散随机变量并画出了概率质量函数:
geom.pmf(k) = (1-p)**(k-1)*p
这里k≥1,p是形状参数:
import numpy as npfrom scipy.stats import geomimport matplotlib.pyplot as pltp = 0.5mean, variance, skewness, kurtosis = geom.stats(p, moments='mvsk')x_var = np.arange(geom.ppf(0.01, p),geom.ppf(0.99, p))plt.plot(x_var, geom.pmf(x_var, p), 'go', ms=5, label='PMF of\geomatric')plt.vlines(x_var, 0, geom.pmf(x_var, p), colors='g', lw=3, alpha=0.5)plt.show()
下面的程序展示了广义帕累托连续随机变量的计算并画出其概率密度函数:
genpareto.pdf(x, c) = (1 + c x)*(-1 - 1/c)# 如果c≥0,则x≥0;如果c<0,则0≤ x≤-1/cimport numpy as npfrom scipy.stats import genparetoimport matplotlib.pyplot as pltc = 0.1mean, variance, skewness, kurtosis = genpareto.stats(c,moments='mvsk')x_val = np.linspace(genpareto.ppf(0.01, c),genpareto.ppf(0.99, c),100)plt.plot(x_val, genpareto.pdf(x_val, c),'b-', lw=3, alpha=0.6,label='PDF of Generic Pareto')plt.show()
下面的程序展示了广义伽马连续型随机变量的计算并画出其概率密度函数:
gengamma.pdf(x, a, c) = abs(c) x*(c*a-1) exp(-x*c) / gamma(a)
这里,r x > 0,a > 0,c != 0。其中,a和c为形状参数:
import numpy as npfrom scipy.stats import gengammaimport matplotlib.pyplot as plta, c = 4.41623854294, 3.11930916792mean, variance, skewness, kurtosis = gengamma.stats(a, c,moments='mvsk')x_var = np.linspace(gengamma.ppf(0.01, a, c),gengamma.ppf(0.99, a, c),100)plt.plot(x_var, gengamma.pdf(x_var, a, c),'b-', lw=3, alpha=0.6,label='PDF of generic Gamma')plt.show()
下面的程序展示了多元正态随机变量的计算并画出其概率密度函数。为简便起见,省略其概率密度函数:
import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import multivariate_normalx_var = np.linspace(5, 25, 20, endpoint=False)y_var = multivariate_normal.pdf(x_var, mean=10, cov=2.5)plt.plot(x_var, y_var)plt.show()
也可以停止这些概率分布以展示其概率分布/质量函数。
10. 多维图像处理(scipy.ndimage)
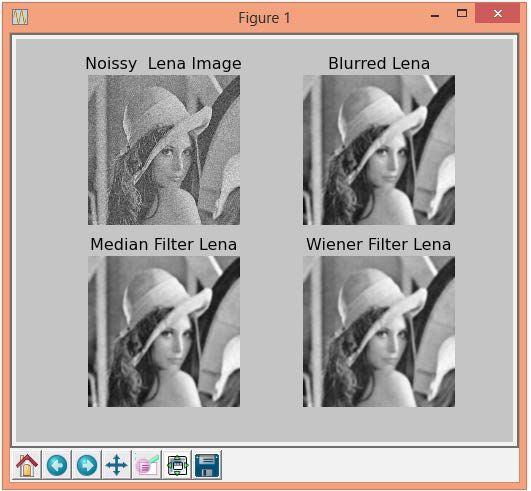
通常图像处理和图像分析可以看作对二维数组的操作。这个包提供了图像处理和图像分析的各种函数。下面的代码处理了图像Lena。首先,这个程序在该图像中加入一些噪声,然后用一些滤波器来去除该噪声。它还展示了有噪声的图像以及分别用高斯滤波器、中值滤波器和signal.wiener滤波器的滤波效果:
import numpy as npfrom scipy import signalfrom scipy import miscfrom scipy import ndimageimport matplotlib.pyplot as pltlena = misc.lena()noisy_lena = np.copy(lena).astype(np.float)noisy_lena += lena.std()*0.5*np.random.standard_normal(lena.shape)f, axarr = plt.subplots(2, 2)axarr[0, 0].imshow(noisy_lena, cmap=plt.cm.gray)axarr[0, 0].axis('off')axarr[0, 0].set_title('Noissy Lena Image')blurred_lena = ndimage.gaussian_filter(noisy_lena, sigma=3)axarr[0, 1].imshow(blurred_lena, cmap=plt.cm.gray)axarr[0, 1].axis('off')axarr[0, 1].set_title('Blurred Lena')median_lena = ndimage.median_filter(blurred_lena, size=5)axarr[1, 0].imshow(median_lena, cmap=plt.cm.gray)axarr[1, 0].axis('off')axarr[1, 0].set_title('Median Filter Lena')wiener_lena = signal.wiener(blurred_lena, (5,5))axarr[1, 1].imshow(wiener_lena, cmap=plt.cm.gray)axarr[1, 1].axis('off')axarr[1, 1].set_title('Wiener Filter Lena')plt.show()
以下截图是上面程序的输出。
11. 聚类
聚类是将一个大的对象集合分成多个组的过程。它用到了一些参数来判定一个对象和该组(也称类)内的对象更相似,而和其他类或组中的对象不相似。
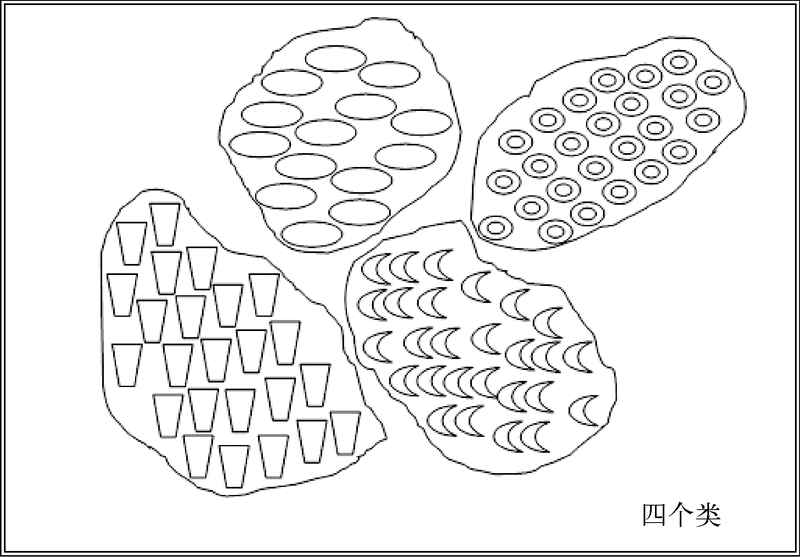
对象分成四个类
SciPy聚类包包括两个模块:向量量化(Vector Quantization,VQ)和层次聚类。VQ模块支持K-means聚类和向量量化。层次聚类模块支持分层聚类和聚合聚类。
来简单地了解这些算法。
向量量化:VQ是使用户通过原型向量的分布来构建概率密度函数模型的信号处理技术。它通过将一个大的向量或点的集合分成多个组来完成建模,这些组在其近邻包括几乎相同数量的点。每个组都用中心点来表示。
K-means:K-means是信号处理中的向量量化技术,广泛用于聚类分析。它按照与聚类中心距离最近的方式,把n个观察值划分为k个聚类。
层次聚类:这种聚类方法是利用观察值建立一组聚类的层级。层次聚类技术大致可以分为以下两种类型。
分离聚类:这是一个生成层次聚类的自上而下的方法。它开始于最顶层的类,随着向下移动不断分裂。
聚合聚类:这是一个自下而上的方法。每个观察值是一个类,该方法在向上移动的过程中将类不断进行配对。
通常层次聚类的结果最终可以用树状图表示,如下图所示。
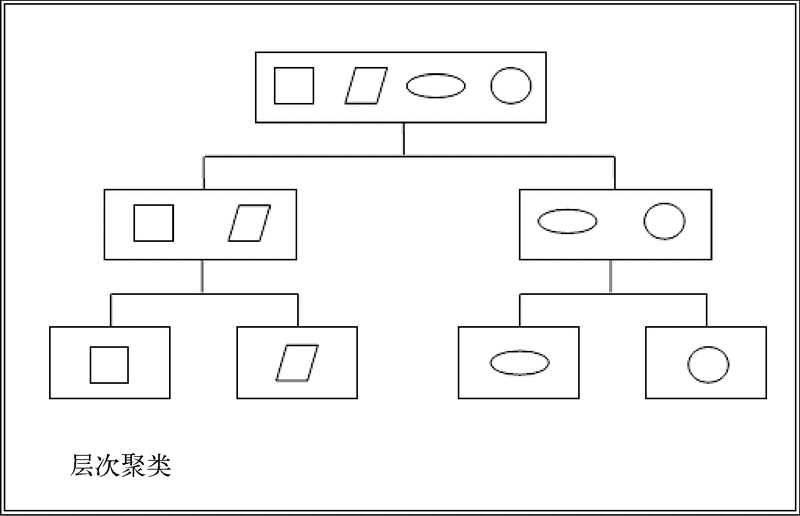
下面的程序展示了K-means聚类和向量量化的例子:
from scipy.cluster.vq import kmeans,vqfrom numpy.random import randfrom numpy import vstack,arrayfrom pylab import plot,showdata_set = vstack((rand(200,2) + array([.5,.5]),rand(200,2)))# K-means聚类分成两个类centroids_of_clusters,_ = kmeans(data_set,2)index,_ = vq(data_set,centroids_of_clusters)plot(data_set[index==0,0],data_set[index==0,1],'ob',data_set[index==1,0],data_set[index==1,1],'or')plot(centroids_of_clusters[:,0],centroids_of_clusters[:,1],'sg',markersize=8)show()# 同样的数据分成三个类centroids_of_clusters,_ = kmeans(data_set,3)index,_ = vq(data_set,centroids_of_clusters)plot(data_set[index==0,0],data_set[index==0,1],'ob',data_set[index==1,0],data_set[index==1,1],'or',data_set[index==2,0],data_set[index==2,1],'og') # 第三个类的点plot(centroids_of_clusters[:,0],centroids_of_clusters[:,1],'sm', markersize=8)show()
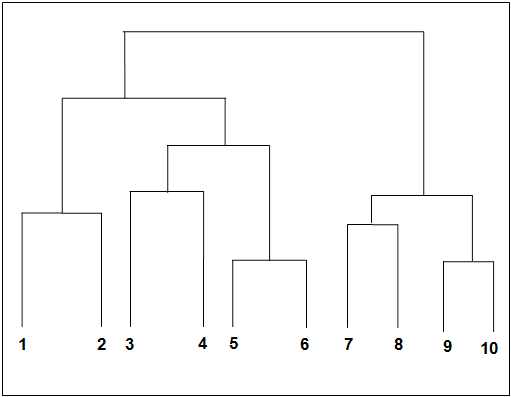
层次聚类的模块有很多函数,这些函数可以包括许多聚类方法,例如将层次聚类切分为扁平聚类的函数、聚合聚类函数、聚类可视化函数、数据结构,以及将层次聚类结果表示为树状图的函数、计算聚类层次的函数、检查链接和不规则指标有效性的推断函数,等等。下面的程序用linkage函数(聚合聚类)和dendrogram函数(层次聚类)画一个示例数据的树状图:
import numpyfrom numpy.random import randfrom matplotlib.pyplot import showfrom scipy.spatial.distance import pdistimport scipy.cluster.hierarchy as schx = rand(8,80)x[0:4,:] *= 2y = pdist(x)z = sch.linkage(y)sch.dendrogram(z)show()
输出结果如下所示。
12. 曲线拟合
构造一个与数据序列最好地拟合的数学函数或曲线的过程即曲线拟合。通常,这个曲线拟合必须满足一些约束条件。曲线拟合的输出可以用于数据可视化,没有数据时也可以通过函数预测结果。曲线拟合也可以用来观察多个变量之间的关系。我们可以用不同类型的曲线做曲线拟合,如直线、多项式、圆锥曲线、三角函数、圆、椭圆等。
下面的程序首先生成了一些带噪声的随机数据。然后它定义了一个line_func函数来表示该模型并做曲线拟合。接下来求解实际参数a和b。最后画出误差:
import numpy as npimport matplotlib.pyplot as pltfrom scipy.optimize import curve_fitxdata = np.random.uniform(0., 50., 80)ydata = 3. * xdata + 2. + np.random.normal(0., 5., 80)plt.plot(xdata, ydata, '.')def line_func(x, a, b):return a x + bopt_param, cov_estimated = curve_fit(line_func, xdata, ydata)errors = np.repeat(5., 80)plt.errorbar(xdata, ydata, yerr=errors, fmt=None)opt_param, cov_estimated = curve_fit(line_func, xdata, ydata,sigma=errors)print "a =", opt_param[0], "+/-", cov_estimated[0,0]*0.5print "b =", opt_param[1], "+/-", cov_estimated[1,1]**0.5plt.errorbar(xdata, ydata, yerr=errors, fmt=None)xnew = np.linspace(0., 50., 80)plt.plot(xnew, line_func(xnew, opt_param[0], opt_param[1]), 'r-')plt.errorbar(xdata, ydata, yerr=errors, fmt=None)plt.plot(xnew, line_func(xnew, *opt_param), 'r-')plt.show()
下面的程序用cos三角函数做曲线拟合:
import numpy as npfrom scipy import optimizeimport pylab as plnp.random.seed(0)def func(x, omega, p):return np.cos(omega * x + p)x = np.linspace(0, 10, 100)y = f(x, 2.5, 3) + .1*np.random.normal(size=100)params, params_cov = optimize.curve_fit(f, x, y)t = np.linspace(0, 10, 500)pl.figure(1)pl.clf()pl.plot(x, y, 'bx')pl.plot(t, f(t, *params), 'r-')pl.show()
13. 文件输入/输出(scipy.io)
SciPy用模块、类和函数提供了一系列文件格式的读和写的支持,这些文件包括:
Matlab文件
ALD文件
Matrix Market文件
无格式的FORTRAN文件
WAV声音文件
ARFF文件
NetCDF文件
下面的程序执行了NetCDF文件的读和写操作:
from scipy.io import netcdf# 创建文件f = netcdf.netcdf_file('TestFile.nc', 'w')f.history = 'Test netCDF File Creation'f.createDimension('age', 12)age = f.createVariable('age', 'i', ('age',))age.units = 'Age of persons in Years'age[:] = np.arange(12)f.close()# 读取文件f = netcdf.netcdf_file('TestFile.nc', 'r')print(f.history)age = f.variables['age']print(age.units)print(age.shape)print(age[-1])f.close()
同样,我们可以对其他类型的文件执行读和写操作。有一个加载文件的子模块,该子模块由WEKA机器学习工具生成。WEKA将文件存储为ARFF格式,该格式为WEKA的标准格式。ARFF是一个可能包含数值、字符串和数据值的文本文件。下面的程序读取和显示了test.arff文件中存储的数据。文件中的内容是@relation foo; @attribute width numeric; @attribute height numeric; @attribute color {red,green,blue,yellow,black}; @data; 5.0,3.25, blue; 4.5,3.75,green; 3.0,4.00,red。
下面的程序读取和显示了该文件内容:
from scipy.io import arfffile1 = open('test.arff')data, meta = arff.loadarff(file1)print dataprint meta
5.3 小结
本章广泛地讨论了如何用Python的NumPy和SciPy包做数值计算。我们通过示例程序来理解这些概念。这一章从NumPy的基本对象开始讨论,然后学习了NumPy的高级功能。
这一章还讨论了SciPy的函数和模块。介绍了SciPy提供的基础函数和特殊函数,以及特殊的模块或子包。也介绍到了一些高级功能,如优化、插值、傅里叶变换、信号处理、线性代数、统计、空间算法、图像处理和文件的输入输出。
下一章将详尽地讨论用SymPy做符号运算或CAS,特别是学习多项式、微积分、求解方程、离散数学、几何和物理的核心功能与扩展功能。
