第 2 章 用scikitlearn估计器分类
用Python语言编写的scikitlearn库,实现了一系列数据挖掘算法,提供通用编程接口、标准化的测试和调参工具,便于用户尝试不同算法对其进行充分测试和查找最优参数值。有大量使用scikitlearn库的算法和工具。
本章讲解数据挖掘通用框架的搭建方法。有了这样一个框架,后续章节就可以把讲解重点放到数据挖掘应用和技术上面。
本章主要介绍如下几个概念。
估计器(Estimator):用于分类、聚类和回归分析。
转换器(Transformer):用于数据预处理和数据转换。
流水线(Pipeline):组合数据挖掘流程,便于再次使用。
2.1 scikitlearn估计器
为帮助用户实现大量分类算法,scikitlearn把相关功能封装成所谓的估计器。估计器用于分类任务,它主要包括以下两个函数。
fit():训练算法,设置内部参数。该函数接收训练集及其类别两个参数。predict():参数为测试集。预测测试集类别,并返回一个包含测试集各条数据类别的数组。
大多数scikitlearn估计器接收和输出的数据格式均为numpy数组或类似格式。
scikitlearn提供了大量估计器,其中有支持向量机(SVM)、随机森林、神经网络等,多数算法本书都会有所涉及。本章先介绍scikitlearn中的近邻算法。
我们需要安装
matplotlib库,作图时会用到。最简单的安装方法就是用pip3来安装,在第1章安装scikitlearn时用过。
$pip3 install matplotlib安装过程中若遇到任何问题,请参考官方给出的安装指南:http://matplotlib.org/users/installing.html。
2.1.1 近邻算法
近邻算法可能是标准数据挖掘算法中最为直观的一种。为了对新个体进行分类,它查找训练集,找到与新个体最相似的那些个体,看看这些个体大多属于哪个类别,就把新个体分到哪个类别。
举例来说,我们要根据三角形更像什么(跟哪种图形离得更近),预测三角形的类别。我们找到三个离它最近的邻居:两个菱形和一个圆。菱形的数量多于圆,因此我们预测三角形的类别为菱形。
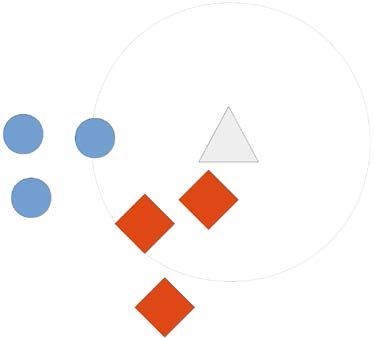
近邻算法几乎可以对任何数据集进行分类,但是,要计算数据集中每两个个体之间的距离,计算量很大。例如,数据集中个体数量为10时,需要计算45对不同个体之间的距离。然而,当个体数量为1000时,要计算大约50万对个体之间的距离!现在有很多提升该算法速度的方法,后续章节会讲到几种。
除了计算量大之外,该算法还有一个问题,就是在特征取离散值的数据集上表现很差。遇到这种情况,应该考虑使用其他算法。
2.1.2 距离度量
距离是数据挖掘的核心概念之一。我们往往需要知道两个个体之间的距离是多少。更进一步说,我们还得能够解决一对个体相对另一对个体是否更相近等问题。这类问题的解决方法,将直接影响分类结果。
人们耳熟能详的距离度量方法就是欧氏距离,即真实距离。假如你在图像中画两个点,用直尺测量这两个点之间的距离,得到的结果就是欧氏距离。稍微正式点来说,它其实是两个特征向量长度平方和的平方根。
欧氏距离确实很直观,但是如果某些特征比其他特征取值大很多,精确度就会比较差。此外,如果很多特征值为0,也就是所谓的稀疏矩阵,结果也不准确。这时可以用其他距离度量方法,常用的有曼哈顿距离和余弦距离。
曼哈顿距离为两个特征在标准坐标系中绝对轴距之和(没有使用平方距离)。拿国际象棋中的车1举例子,这样更形象。假如车每次只能走一格,那么它走到当前格子对角线那头,所走的距离就是曼哈顿距离。虽然异常值也会影响分类结果,但是其所受的影响要比欧氏距离小得多。
1国际象棋中车的走法跟我国象棋中车的走法相同,只能沿水平或垂直方向移动。——译者注
余弦距离更适合解决异常值和数据稀疏问题。直观上讲,余弦距离指的是特征向量夹角的余弦值。下面为以上三种距离的示意图。
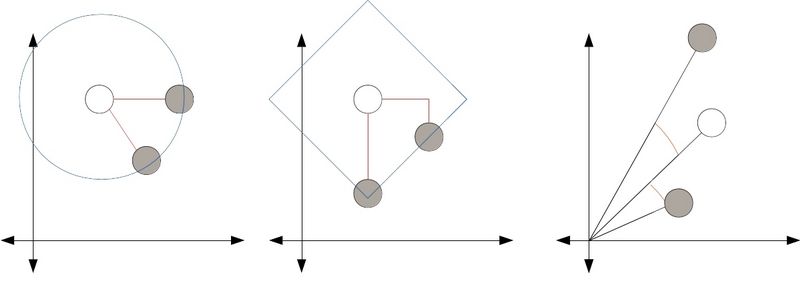
在上面每张图中,两个灰圆与白圆之间的距离是相等的。左图是欧氏距离,因此两个灰圆都落在以白圆为圆心的同一个圆的圆周上,可以用尺子量量看。中间这幅图表示的是曼哈顿距离,它指的是从灰圆到白圆所走的横向和纵向距离之和,也叫街区距离(City Block),测量时要想象棋中车的走法。右图是余弦距离示意图,计算夹角之间的余弦值,忽略特征向量的长度。
采用哪种距离度量方法对最终结果有很大影响。例如,你的数据集有很多特征,但是如果任意一对个体之间的欧氏距离都相等,那么你就没法通过欧氏距离进行比较了!曼哈顿距离在某些情况下具有更高的稳定性,但是如果数据集中某些特征值很大,用曼哈顿距离的话,这些特征会掩盖其他特征间的邻近关系。最后,再来说说余弦距离,它适用于特征向量很多的情况,但是它丢弃了向量长度所包含的在某些场景下可能会很有用的一些信息。
本章,我们主要介绍欧氏距离,其他距离后面章节再介绍。
2.1.3 加载数据集
即将用到的数据集叫作电离层(Ionosphere),这些数据是由高频天线收集的。这些天线的目的是侦测在电离层和高层大气中存不存在由自由电子组成的特殊结构。如果一条数据能给出特殊结构存在的证据,这条数据就属于好的那一类(在数据集中用“g”表示),否则就是坏的(用“b”表示)。我们要做的就是建立分类器,自动判断这些数据的好坏。

(图像来自https://www.flickr.com/photos/geckzilla/16149273389/)
Ionosphere数据集可以从UCI机器学习数据库下载,该数据库包含大量数据集,可用于多种数据挖掘任务。打开http://archive.ics.uci.edu/ml/datasets/Ionosphere,点击Data Folder。在随后打开的页面中,下载ionosphere.data和ionosphere.names文件。把这两个文件保存到用户主目录下的Data文件夹中。
主目录的位置取决于操作系统。Windows系统中通常为C:\Documents and Settings\username。Mac和Linux系统中为/home/username。如果你不确定,可以使用下面的Python代码输出主目录所在位置:
import osprint(os.path.expanduser("~"))
该数据集每行有35个值,前34个为17座天线采集的数据(每座天线采集两个数据)。最后一个值不是“g”就是“b”,表示数据的好坏,即是否提供了有价值的信息。
启动IPython Notebook服务器,新建名为Ionosphere Nearest Neighbors的笔记本文件。
首先,导入numpy和csv库,下面会用到。
import numpy as npimport csv
加载数据集前,用Data文件夹路径、数据集所在的文件夹名称和数据集名称组合成数据集文件的完整路径。
data_filename = os.path.join(data_folder, "Ionosphere","ionosphere.data")
创建Numpy数组X和y存放数据集。数据集大小已知,共有351行34列。在以后的实际工作中,如果你不知道数据集大小也没关系——后面章节会讲如何在不知道数据集大小的情况下加载它,具体怎么做现在不知道也没关系。
X = np.zeros((351, 34), dtype='float')y = np.zeros((351,), dtype='bool')
Ionosphere数据集文件为CSV(Comma-Separated Values,用逗号分隔数据项)格式,这是常用的数据集存储格式。我们用csv模块来导入数据集文件,并创建csv阅读器对象。
with open(data_filename, 'r') as input_file:reader = csv.reader(input_file)
接着,遍历文件中的每一行数据。每行数据代表一组测量结果,我们可以将其称作数据集中的一个个体。用枚举函数来获得每行的索引号,在下面更新数据集X中的某一个体时会用到行号。
for i, row in enumerate(reader):
获取每一个个体的前34个值,将其强制转化为浮点型,保存到X中。
data = [float(datum) for datum in row[:-1]]X[i] = data
最后,获取每个个体最后一个表示类别的值,把字母转化为数字,如果类别为“g”,值为1,否则值为0。
y[i] = row[-1] == 'g'
到此,我们就把数据集读到了数组X中,类别读入了数组y中,与我们在上一章的做法相同。
2.1.4 努力实现流程标准化
正如本章开头讲过的,scikitlearn估计器由两大函数组成:fit()和predict()。用fit方法在训练集上完成模型的创建,用predict方法在测试集上评估效果。
首先,需要创建训练集和测试集。导入并运行train_test_split函数。
from sklearn.cross_validation import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, random_state=14)
然后,导入 K 近邻分类器这个类,并为其初始化一个实例。现阶段,参数用默认的即可,后面再讲参数调优。该算法默认选择5个近邻作为分类依据。
from sklearn.neighbors import KNeighborsClassifierestimator = KNeighborsClassifier()
估计器创建好后,接下来就要用训练数据进行训练。K 近邻估计器分析训练集中的数据,比较待分类的新数据点和训练集中的数据,找到新数据点的近邻。
estimator.fit(X_train, y_train)
接着,用测试集测试算法,评估它在测试集上的表现。
y_predicted = estimator.predict(X_test)accuracy = np.mean(y_test == y_predicted) * 100print("The accuracy is {0:.1f}%".format(accuracy))
正确率为86.4%。使用默认参数,只用少数几行代码就能达到这个效果,真是很厉害!虽然scikitlearn提供的大多数默认参数适用范围广,效果也不错,但我们还是要学着根据实验的实际情况,尽可能选用合适的参数值,争取达到最佳效果。
2.1.5 运行算法
在先前的几个实验中,我们把数据集分为训练集和测试集,用训练集训练算法,在测试集上评估效果。倘若碰巧走运,测试集很简单,我们就会觉得算法表现很出色。反之,我们可能会怀疑算法很糟糕。也许由于我们一时不走运,就把一个其实很不错的算法给无情抛弃了,这岂不是很可惜。
交叉检验能解决上述一次性测试所带来的问题。既然只切一次有问题,那就多切几次,多进行几次实验。每次切分时,都要保证这次得到的训练集和测试集与上次不一样,还要确保每条数据都只能用来测试一次。算法描述如下。
(1) 将整个大数据集分为几个部分(fold2)。
2行话叫“折”。——译者注
(2) 对于每一部分执行以下操作:
将其中一部分作为当前测试集
用剩余部分训练算法
在当前测试集上测试算法
(3) 记录每次得分及平均得分。
(4) 在上述过程中,每条数据只能在测试集中出现一次,以减少(但不能完全规避)运气成分。
书中同一章的代码,前后是紧密联系的,所以需要把它们放到一个IPython Notebook笔记本文件中,除非我告诉你不必这么做。
scikitlearn提供了几种交叉检验方法。有个辅助函数实现了上述交叉检验步骤,现在把它导进来。
from sklearn.cross_validation import cross_val_score

cross_val_score默认使用Stratified K Fold方法切分数据集,它大体上保证切分后得到的子数据集中类别分布相同,以避免某些子数据集出现类别分布失衡的情况。这个默认做法很不错,现阶段就不再把它搞复杂了。
我们就来试试这个函数吧,把完整的数据集和类别值传给它。
scores = cross_val_score(estimator, X, y, scoring='accuracy')average_accuracy = np.mean(scores) * 100print("The average accuracy is {0:.1f}%".format(average_accuracy))
哦,结果为82.3%,较之前稍微差点,但考虑到我们还没有尝试调整参数,这个结果还是相当不错的。下一节,我们就来研究怎么通过调整参数达到更理想的效果。
2.1.6 设置参数
几乎所有的数据挖掘算法都允许用户设置参数,这样做的好处是增强算法的泛化能力。但是,参数设置可是项技术活,选取好的参数值跟数据集的特征息息相关。
近邻算法有多个参数,最重要的是选取多少个近邻作为预测依据。scikitlearn管这个参数叫n_neighbors。下图给出两个极端的例子,n_neighbors过小时,分类结果容易受干扰,随机性很强。相反,如果n_neighbors过大,实际近邻的影响将削弱。
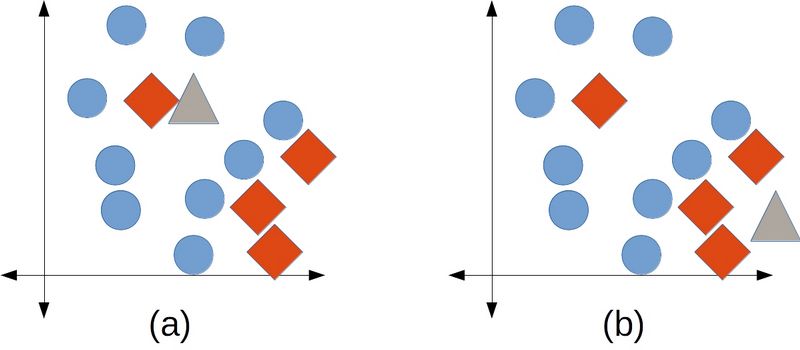
左图(a)中,我们通常希望把测试数据(三角形)归到圆形类别。然而,如果n_neighbors的值为1,由于三角形附近红色菱形(很可能是噪音)的存在,导致分类结果为菱形,虽然菱形集中在右下角区域。右图(b)中,我们希望将测试数据归到菱形类别。然而,如果n_neighbors值为7,三个最近的邻居(都是菱形)被四个圆形给击败了,三角形也因此被归到圆形类别。
如果想测试一系列n_neighbors的值,比如从1到20,可以重复进行多次实验,观察不同的参数值所带来的结果之间的差异。
avg_scores = []all_scores = []parameter_values = list(range(1, 21)) # Include 20for n_neighbors in parameter_values:estimator = KNeighborsClassifier(n_neighbors=n_neighbors)scores = cross_val_score(estimator, X, y, scoring='accuracy')
把不同n_neighbors值的得分和平均分保存起来,留作分析用。
avg_scores.append(np.mean(scores))all_scores.append(scores)
为了看起来更直观,我们可以用图表来表示n_neighbors的不同取值和分类正确率之间的关系。首先需要告诉IPython Notebook,我们要在笔记本中作图。
%matplotlib inline
然后,从matplotlib库导入pyplot,参数为近邻数和平均正确率。
from matplotlib import pyplot as plt plt.plot(parameter_values,avg_scores, '-o')
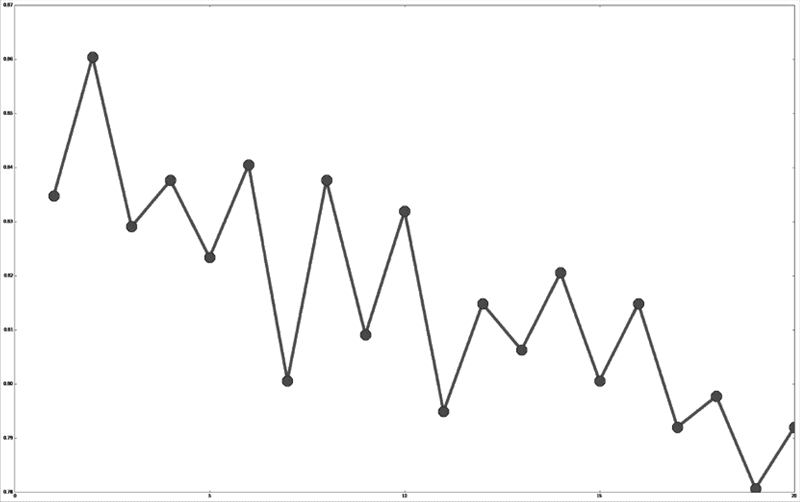
从上图可以看到,虽然有很多曲折变化,但整体趋势是随着近邻数的增加,正确率不断下降。
2.2 流水线在预处理中的应用
现实中,物体不同特征的取值范围会非常广,它们的值域可能存在天壤之别。例如,测量动物的属性,会得到下面这样千差万别的特征值。
腿的数量:大多数动物有0到8条腿,但也有比这多得多的!
体重:从几微克到上百吨都有可能,有的蓝鲸重达190吨!
心脏数量:0到5之间,蚯蚓就有5颗心脏。
对于借助数学方法来比较特征的算法而言,它们很难理解特征在规模、范围和单位上的差异。如果我们在多种算法中使用上述特征,体重由于数值较大,可能都会是最显著的特征,但特征值大小实际上与该特征的分类效果没有任何关系。
不同特征的取值范围千差万别,常见的解决方法是对不同的特征进行规范化,使它们的特征值落在相同的值域或从属于某几个确定的类别,比如小、中和大。一旦解决这个问题,不同的特征类型对算法的影响将大大降低,分类正确率就能有大幅提升。
选择最具区分度的特征、创建新特征等都属于预处理的范畴。scikitlearn的预处理工具叫作转换器(Transformer),它接受原始数据集,返回转换后的数据集。除了处理数值型特征,转换器还能用来抽取特征。在这里,我们只看下对数值型特征的预处理方法。
2.2.1 预处理示例
为了讲解需要,先来对Ionosphere数据集做些破坏。虽然这里的麻烦是人为制造的,但是这些问题在很多真实数据集里都存在。首先,为了不破坏原来的数据集,我们为其创建一个副本。
X_broken = np.array(X)
接下来,我们就要捣乱了,将奇数列的特征值除以10。
X_broken[:,::2] /= 10
理论上讲,这样做对结果影响应该不大。毕竟,除以10之后,各个特征相差不大。主要的问题是,数值范围变了,奇数列的第二个特征要比偶数列的大。再次计算正确率看一下效果。
estimator = KNeighborsClassifier()original_scores = cross_val_score(estimator, X, y,scoring='accuracy')print("The original average accuracy for is{0:.1f}%".format(np.mean(original_scores) 100))broken_scores = cross_val_score(estimator, X_broken, y,scoring='accuracy')print("The 'broken' average accuracy for is{0:.1f}%".format(np.mean(broken_scores) 100))
还记得吧,在原始数据集上的正确率为82.3%,这次跌至71.5%。把特征值转变到0到1之间就能解决这个问题。
2.2.2 标准预处理
我们接下来用MinMaxScaler类进行基于特征的规范化。在本章的笔记本文件中,接着之前的代码写,首先导入所需的类。
from sklearn.preprocessing import MinMaxScaler
这个类可以把每个特征的值域规范化为0到1之间。最小值用0代替,最大值用1代替,其余值介于两者之间。
接下来,对数据集X进行预处理。我们在预处理器MinMaxScaler上调用转换函数。有些转换器要求像训练分类器那样先进行训练,但是MinMaxScaler不需要,直接调用fit_transform()函数,即可完成训练和转换。
X_transformed = MinMaxScaler().fit_transform(X)
X_transformed与X行列数相等,为同型矩阵。然而,前者每列值的值域为0到1。
还有很多其他类似的规范化方法,对于其他类型的应用和特征类型会很有用。
为使每条数据各特征值的和为1,使用
sklearn.preprocessing.Normalizer。为使各特征的均值为0,方差为1,使用
sklearn.preprocessing.StandardScaler,常用作规范化的基准。为将数值型特征的二值化,使用
sklearn.preprocessing.Binarizer,大于阈值的为1,反之为0。
后续章节,将会组合运用上述预处理方法及其他转换器对象。
2.2.3 组装起来
现在我们把前几节所讲的代码组合起来,创建一套完整的工作流,处理被破坏过的数据集。
X_transformed = MinMaxScaler().fit_transform(X_broken)estimator = KNeighborsClassifier()transformed_scores = cross_val_score(estimator, X_transformed, y,scoring='accuracy')print("The average accuracy for is{0:.1f}%".format(np.mean(transformed_scores) * 100))
正确率再次升到82.3%。MinMaxScaler将特征规范化到相同的值域,这样特征就不会仅仅因为值大而具备更强的区分度。简单总结下,异常值会影响近邻算法,不同算法对值域大小的敏感度不同。
2.3 流水线
随着实验的增加,操作的复杂程度也在提高。我们可能需要切分数据集,对特征进行二值化处理,以特征或数据集中的个体为基础规范化数据,除此之外还可能需要其他各种操作。
要跟踪记录所有这些操作可不容易,如果中间出点问题,先前实验的结果将很难再现。常见问题有落下步骤,数据转换错误,或进行了不必要的转换操作等。
另一个问题就是代码的先后顺序。上一节,我们创建了X_transformed数据集,然后创建了一个新的估计器用于交叉检验。如果有多个步骤,就需要跟踪代码中对数据集进行的每一步操作。
流水线结构就是用来解决这些问题的(当然不限于这些,下一章会讲到它在其他方面的应用)。流水线把这些步骤保存到数据挖掘的工作流中。之后你就可以用它们读入数据,做各种必要的预处理,然后给出预测结果。我们可以在cross_val_score等接收估计器的函数中使用流水线。创建流水线前,先导入Pipeline对象。
from sklearn.pipeline import Pipeline
流水线的输入为一连串的数据挖掘步骤,其中最后一步必须是估计器,前几步是转换器。输入的数据集经过转换器的处理后,输出的结果作为下一步的输入。最后,用位于流水线最后一步的估计器对数据进行分类。我们流水线分为两大步。
(1) 用MinMaxScaler将特征取值范围规范到0~1。
(2) 指定KNeighborsClassifier分类器。
每一步都用元组(‘名称’,步骤)来表示。现在来创建流水线。
scaling_pipeline = Pipeline([('scale', MinMaxScaler()),('predict', KNeighborsClassifier())])
流水线的核心是元素为元组的列表。第一个元组规范特征取值范围,第二个元组实现预测功能。我们把第一步叫作规范特征取值(scale),第二步叫作预测(predict),也可以用其他名字。元组的第二部分是实际的转换器对象或估计器对象。
流水线写好后,运行它很简单。使用先前用到的交叉检验代码看一下实际效果。
scores = cross_val_score(scaling_pipeline, X_broken, y,scoring='accuracy')print("The pipeline scored an average accuracy for is {0:.1f}%".format(np.mean(transformed_scores) * 100))
运行结果跟之前一样(82.3%),表明我们这次用到的步骤跟之前相同。
后续章节会使用更高级的测试方法,而设置流水线就很有必要,因为它能确保代码的复杂程度不至于超出掌控范围。
2.4 小结
本章,我们用scikitlearn库提供的几个方法,创建了运行和评估数据挖掘模型的标准工作流。还介绍了近邻算法,scikitlearn将其封装为一个估计器,使用起来很简单:首先调用fit函数在训练集上进行训练,然后用predict函数在测试集上评估效果。
本章还通过解决不同特征值域影响分类效果的问题,讲解了预处理方法,主要用到了转换器对象和MinMaxScaler类。它们也有训练(fit)和转换方法,在转换阶段,接收数据集,返回处理过的数据集。
下一章,我们尝试把学到的这些概念应用到一个大一点的例子上,学着预测NBA(美国职业篮球联赛)比赛结果,其中使用的数据集可是真实的哦。
