第 4 章　用亲和性分析方法推荐电影

第 4 章　用亲和性分析方法推荐电影

本章学习如何用亲和性分析方法找出在什么情况下两个对象经常一起出现。通俗来讲，这也叫“购物篮分析”，因为曾有人用它找出哪些商品经常一起出售。

第3章关注的对象为球队，并用特征描述球队。本章所用到的电影评分数据有所不同，我们所关注的对象（电影）埋在数据中。本章数据挖掘任务的目标是找出对象同时出现的情况，也就是寻找用户同时喜欢几部电影的情况。

本章主要涉及以下几个概念。

亲和性分析
用Apriori算法挖掘关联特征
电影推荐
数据稀疏问题

4.1　亲和性分析

亲和性分析用来找出两个对象共同出现的情况。而前几章，我们关注的是同种对象之间的相似度。亲和性分析所用的数据通常为类似于交易信息的数据。从直观上来看，这些数据就像是商店的交易数据——从中能看出哪些商品是顾客一起购买的。

然而，亲和性分析方法的应用场景有很多，比如：

欺诈检测
顾客区分
软件优化
产品推荐

亲和性分析比分类更具探索性，因为通常我们无法拿到像在很多分类任务中所用的那样完整的数据集。例如，在电影推荐任务中，我们拿到的是不同用户对不同电影的评价。但是，每个用户不可能评价过所有电影，这就给亲和性分析带来一个不容忽视的大难题。如果用户没有评价过一部电影，是因为他们不喜欢这部电影（据此就不推荐给他们），还是因为他们出于别的原因还没有评价？

本章不对上述问题做出解答，但是我们要思考数据集中类似这样的潜在问题该怎么解决。这些思考有助于提升推荐算法的准确性。

4.1.1　亲和性分析算法

我们在第1章介绍了一种基础的亲和性分析算法，尝试了所有可能的规则组合，计算了每条规则的置信度和支持度，并根据这两个标准进行排序，选取最佳规则。

然而，这个方法效率不高。好在第1章所使用的数据集中，每条交易数据只涉及五种商品。但现实并非如此，即使是再不起眼的小卖铺出售的商品也达上百种之多，网店更是有成千上万种商品（甚至几百万种！）。如果规则生成方法像第1章那样过于简单，计算这些规则所需要的时间复杂度将呈指数级增长。随着商品数量的增加，计算所有规则所需的时间增长得很快。更具体地说，所有可能的规则数量是2ⁿ-1。数据集有5个特征，可能的规则就有31条；有10个特征，可能的规则就有1023条；仅仅有100个特征，规则数就能达到30位数字。即使计算能力大幅提升也未必能赶上在线商品的增长速度。因此，与其跟计算机过不去，不如寻找更加聪明的算法。

Apriori算法可以说是经典的亲和性分析算法。它只从数据集中频繁出现的商品中选取共同出现的商品组成频繁项集（frequent itemset），避免了上述复杂度呈指数级增长的问题。一旦找到频繁项集，生成关联规则就很容易了。

Apriori算法背后的原理简洁却不失巧妙。首先，确保了规则在数据集中有足够的支持度。Apriori算法的一个重要参数就是最小支持度。比如，要生成包含商品A、B的频繁项集（A, B），要求支持度至少为30，那么A和B都必须至少在数据集中出现30次。更大的频繁项集也要遵守该项约定，比如要生成频繁项集（A, B, C, D），那么子集(A, B, C)必须是频繁项集（当然D自己也要满足最小支持度标准）。

生成频繁项集后，将不再考虑其他可能的却不够频繁的项集（这样的集合有很多），从而大大减少测试新规则所需的时间。

其他亲和性分析算法有Eclat和频繁项集挖掘算法（FP-growth）。从数据挖掘角度看，这些算法比起基础的Apriori算法有很多改进，性能也有进一步提升。接下来，先来看一下最基础的Apriori算法。

4.1.2　选择参数

挖掘亲和性分析所用的关联规则之前，我们先用Apriori算法生成频繁项集。接着，通过检测频繁项集中前提和结论的组合，生成关联规则（例如，如果用户喜欢电影X，那么他很可能喜欢电影Y）。

第一个阶段，需要为Apriori算法指定一个项集要成为频繁项集所需的最小支持度。任何小于最小支持度的项集将不再考虑。如果最小支持度值过小，Apriori算法要检测大量的项集，会拖慢的运行速度；最小支持度值过大的话，则只有很少的频繁项集。

找出频繁项集后，在第二个阶段，根据置信度选取关联规则。可以设定最小置信度，返回一部分规则，或者返回所有规则，让用户自己选。

本章，我们设定最小置信度，只返回高于它的规则。置信度过低将会导致规则支持度高，正确率低；置信度过高，导致正确率高，但是返回的规则少。

4.2　电影推荐问题

产品推荐技术是门大生意。网店经常用它向潜在用户推荐他们可能购买的产品。好的推荐算法能带来更高的销售业绩。每年有几百万乃至几千万用户进行网购，向他们推荐更多的商品，潜在收益着实可观。

产品推荐问题被人们研究了多年，但它一直不温不火，直到2007年到2009年间，Netflix公司推出数据建模大赛，并设立Netflix Prize奖项之后，才得到迅猛发展。该竞赛意在寻找比Netflix公司所使用的预测用户为电影打分的系统更准确的解决方案。最后获奖队伍以比现有系统高10个百分点的优势胜出。虽然这个改进看起来不是很大，但是Netflix公司却能借助它实现更精准的电影推荐服务，从而多赚上百万美元。

4.2.1　获取数据集

自打Netflix Prize奖项设立以来，美国明尼苏达大学的Grouplens研究团队公开了一系列用于测试推荐算法的数据集。其中，就包括几个大小不同的电影评分数据集，分别有10万、100万和1000万条电影评分数据。

数据集下载地址为http://grouplens.org/datasets/movielens/。本章将使用包含10万条数据的MovieLens数据集。下载数据集，解压到你的Data文件夹。启动IPython Notebook笔记本，输入以下代码。

import os
import pandas as pd
data_folder = os.path.join(os.path.expanduser("~"), "Data",
  "ml-100k")
ratings_filename = os.path.join(data_folder, "u.data")

确保ratings_filename指向解压后得到的文件夹中的u.data文件。

4.2.2　用pandas加载数据

MovieLens数据集非常规整，但是有几点跟pandas.read_csv方法的默认设置有出入，所以要调整参数设置。第一个问题是数据集每行的几个数据之间用制表符而不是逗号分隔。其次，没有表头，这表示数据集的第一行就是数据部分，我们需要手动为各列添加名称。

加载数据集时，把分隔符设置为制表符，告诉pandas不要把第一行作为表头（header=None），设置好各列的名称。代码如下：

all_ratings = pd.read_csv(ratings_filename, delimiter="\t",
    header=None, names = ["UserID", "MovieID", "Rating", "Datetime"])

虽然本章用不到，还是稍微提一下，你可以用下面的代码解析时间戳数据。

all_ratings["Datetime"] = pd.to_datetime(all_ratings['Datetime'],
  unit='s')

运行下面的代码，看一下前五条记录。

all_ratings[:5]

输出结果如下。

	UserID	MovieID	Rating	Datetime
0	196	242	3	1997-12-04 15:55:49
1	186	302	3	1998-04-04 19:22:22
2	22	377	1	1997-11-07 07:18:36
3	244	51	2	1997-11-27 05:02:03
4	166	346	1	1998-02-02 05:33:16

4.2.3　稀疏数据格式

这是一个稀疏数据集，我们可以将每一行想象成巨大特征矩阵的一个格子，前几章用到过这种矩阵。在这个矩阵中，每一行表示一个用户，每一列为一部电影。第一列为每一个用户给第一部电影打的分数，第二列为每一个用户给第二部电影打的分数，以此类推。

数据集中有1000名用户和1700部电影，这就意味着整个矩阵很大。将矩阵读到内存中及在它基础上进行计算可能存在难度。然而，这个矩阵的很多格子都是空的，也就是对大部分用户来说，他们只给少数几部电影打过分。比如用户#213没有为电影#675打过分，大部分用户没有为大部分电影打过分。

用上述图表中的格式也能表示矩阵，且更为紧凑。序号为0的那一行表示，用户#196在1997年12月4日为电影#242打了3分（满分是5分）。

任何没有出现在数据集中的用户和电影组合表示它们实际上是不存在的。这比起在内存中保存大量的0，节省了很多空间。这种格式叫作稀疏矩阵（sparse matrix）。根据经验来说，如果数据集中60%或以上的数据为0，就应该考虑使用稀疏矩阵，从而节省不少空间。

在对稀疏矩阵进行计算时，我们关注的通常不是那些不存在的数据，不会去比较众多的0值，相反我们关注的是现有数据，并对它们进行比较。

4.3　Apriori算法的实现

本章数据挖掘的目标是生成如下形式的规则：如果用户喜欢某些电影，那么他们也会喜欢这部电影。作为对上述规则的扩展，我们还将讨论喜欢某几部电影的用户，是否喜欢另一部电影。

要解决以上问题，首先要确定用户是不是喜欢某一部电影。为此创建新特征Favorable，若用户喜欢该电影，值为True。

all_ratings["Favorable"] = all_ratings["Rating"] > 3

我们在数据集中看一下这个新特征。

all_ratings[10:15]

	UserID	MovieID	Rating	Datetime	Favorable
10	62	257	2	1997-11-12 22:07:14	False
11	286	1014	5	1997-11-17 15:38:45	True
12	200	222	5	1997-10-05 09:05:40	True
13	210	40	3	1998-03-27 21:59:54	False
14	224	29	3	1998-02-21 23:40:57	False

从数据集中选取一部分数据用作训练集，这能有效减少搜索空间，提升Apriori算法的速度。我们取前200名用户的打分数据。

ratings = all_ratings[all_ratings['UserID'].isin(range(200))]

接下来，新建一个数据集，只包括用户喜欢某部电影的数据行。

favorable_ratings = ratings[ratings["Favorable"]]

在生成项集时，需要搜索用户喜欢的电影。因此，接下来，我们需要知道每个用户各喜欢哪些电影，按照User ID进行分组，并遍历每个用户看过的每一部电影。

favorable_reviews_by_users = dict((k, frozenset(v.values))
                                   for k, v in favorable_ratings
                                   groupby("UserID")["MovieID"])

上面的代码把v.values存储为frozenset，便于快速判断用户是否为某部电影打过分。对于这种操作，集合比列表速度快，在后面代码中还会用到。

最后，创建一个数据框，以便了解每部电影的影迷数量。

num_favorable_by_movie = ratings[["MovieID", "Favorable"]].
  groupby("MovieID").sum()

用以下代码查看最受欢迎的五部电影。

num_favorable_by_movie.sort("Favorable", ascending=False)[:5]

输出结果如下：

MovieID	Favorable
50	100
100	89
258	83
181	79
174	74

4.3.1　Apriori算法

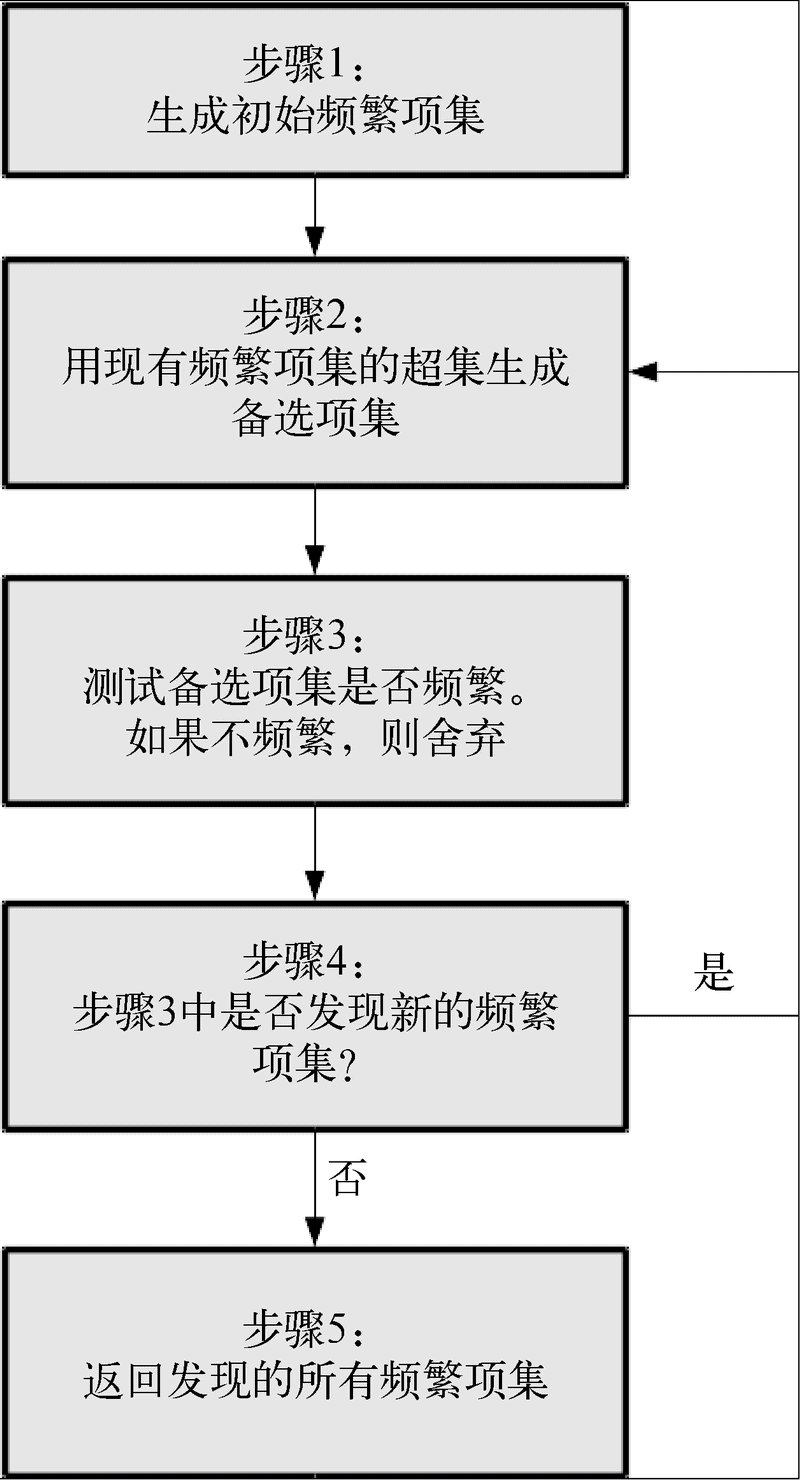
Apriori算法是亲和性分析的一部分，专门用于查找数据集中的频繁项集。基本流程是从前一步找到的频繁项集中找到新的备选集合，接着检测备选集合的频繁程度是否够高，然后算法像下面这样进行迭代。

(1) 把各项目放到只包含自己的项集中，生成最初的频繁项集。只使用达到最小支持度的项目。

(2) 查找现有频繁项集的超集，发现新的频繁项集，并用其生成新的备选项集。

(3) 测试新生成的备选项集的频繁程度，如果不够频繁，则舍弃。如果没有新的频繁项集，就跳到最后一步。

(4) 存储新发现的频繁项集，跳到步骤(2)。

(5) 返回发现的所有频繁项集。

整个过程表示如下。

第 4 章　用亲和性分析方法推荐电影 - 图1

4.3.2　实现

Apriori算法第一次迭代时，新发现的项集长度为2，它们是步骤(1)中创建的项集的超集。第二次迭代（经过步骤(4)）中，新发现的项集长度为3。这有助于我们快速识别步骤(2)所需的项集。

我们把发现的频繁项集保存到以项集长度为键的字典中，便于根据长度查找，这样就可以找到最新发现的频繁项集。下面的代码初始化一个字典。

frequent_itemsets = {}

我们还需要确定项集要成为频繁项集所需的最小支持度。这个值需要根据数据集的具体情况来设定，可自行尝试其他值，建议每次只改动10个百分点，即使这样你可能也会发现算法运行时间变动很大！下面，设置最小支持度。

min_support = 50

我们先来实现Apriori算法的第一步，为每一部电影生成只包含它自己的项集，检测它是否够频繁。电影编号使用frozenset，后面要用到集合操作。此外，它们也可以用作字典的键（普通集合不可以）。代码如下：

frequent_itemsets[1] = dict((frozenset((movie_id,)),
                                 row["Favorable"])
                                 for movie_id, row in num_favorable_
                                   by_movie.iterrows()
                                 if row["Favorable"] > min_support)

接着，用一个函数来实现步骤(2)和(3)，它接收新发现的频繁项集，创建超集，检测频繁程度。下面为函数声明及字典初始化代码。

from collections import defaultdict
def find_frequent_itemsets(favorable_reviews_by_users, k_1_itemsets,
min_support):
    counts = defaultdict(int)

经验告诉我们，要尽量减少遍历数据的次数，所以每次调用函数时，再遍历数据。这样做效果不是很明显（因为数据集相对较小），但是数据集更大的情况下，就很有必要。我们来遍历所有用户和他们的打分数据。

    for user, reviews in favorable_reviews_by_users.items():

接着，遍历前面找出的项集，判断它们是否是当前评分项集的子集。如果是，表明用户已经为子集中的电影打过分。代码如下：

        for itemset in k_1_itemsets:
            if itemset.issubset(reviews):

接下来，遍历用户打过分却没有出现在项集里的电影，用它生成超集，更新该项集的计数。代码如下：

                for other_reviewed_movie in reviews - itemset:
                    current_superset = itemset | frozenset((other_
                                     reviewed_movie,))
                    counts[current_superset] += 1

函数最后检测达到支持度要求的项集，看它的频繁程度够不够，并返回其中的频繁项集。

    return dict([(itemset, frequency) for itemset, frequency in
counts.items() if frequency >= min_support])

创建循环，运行Apriori算法，存储算法运行过程中发现的新项集。循环体中，k 表示即将发现的频繁项集的长度，用键 k-1 可以从frequent_itemsets字典中获取刚发现的频繁项集。新发现的频繁项集以长度为键，将其保存到字典中。代码如下：

for k in range(2, 20):
    cur_frequent_itemsets =
      find_frequent_itemsets(favorable_reviews_by_users,
        frequent_itemsets[k-1],
          min_support)
      frequent_itemsets[k] = cur_frequent_itemsets

如果在上述循环中没能找到任何新的频繁项集，就跳出循环（输出信息，告知我们没能找到长度为 k 的频繁项集）。

    if len(cur_frequent_itemsets) == 0:
        print("Did not find any frequent itemsets of length {}".
          format(k))
        sys.stdout.flush()
        break

　用sys.stdout.flush()方法，确保代码还在运行时，把缓冲区内容输出到终端。有时，在位于笔记本文件特定格子的大型循环中，代码结束运行前不会输出，用flush方法可以保证及时输出。但是，该方法不宜过多使用——flush操作（输出也是）所带来的计算开销会拖慢程序的运行速度。

如果确实找到了频繁项集，我们也让程序输出信息，告知我们它会再次运行。因为算法运行时间很长，所以每隔一段时间输出一下状态是很有必要的！代码如下：

    else:
        print("I found {} frequent itemsets of length
        {}".format(len(cur_frequent_itemsets), k))
        sys.stdout.flush()

最后，循环结束，我们对只有一个元素的项集不再感兴趣——它们对生成关联规则没有用处——生成关联规则至少需要两个项目。删除长度为1的项集。代码如下：

del frequent_itemsets[1]

上面这些代码要好几分钟才能运行完，老机器需要的时间更长。如果你在本地运行代码有问题，可以考虑使用云主机提升速度，具体细节请见附录。

上述代码返回了不同长度的1718个频繁项集。你也许会发现随着项集长度的增加，项集数随着可用规则的增加而增长一段时间后才开始变少，减少是因为项集达不到最低支持度要求。项集的减少是Apriori算法的优点之一。如果我们搜索所有可能的项集（不只是频繁项集的超集），判断多余项集的频繁程度需要成千上万次查询。

4.4　抽取关联规则

Apriori算法结束后，我们得到了一系列频繁项集，这还不算是真正意义上的关联规则，但是很接近了。频繁项集是一组达到最小支持度的项目，而关联规则由前提和结论组成。

我们可以从频繁项集中抽取出关联规则，把其中几部电影作为前提，另一部电影作为结论组成如下形式的规则：如果用户喜欢前提中的所有电影，那么他们也会喜欢结论中的电影。

每一个项集都可用这种方式生成一条规则。

下面的代码通过遍历不同长度的频繁项集，为每个项集生成规则。

candidate_rules = []
for itemset_length, itemset_counts in frequent_itemsets.items():
    for itemset in itemset_counts.keys():

然后，遍历项集中的每一部电影，把它作为结论。项集中的其他电影作为前提，用前提和结论组成备选规则。

        for conclusion in itemset:
            premise = itemset - set((conclusion,))
            candidate_rules.append((premise, conclusion))

这样就能得到大量备选规则。通过以下代码查看前五条规则。

print(candidate_rules[:5])

输出结果如下：

[(frozenset({79}), 258), (frozenset({258}), 79), (frozenset({50}),
  64), (frozenset({64}), 50), (frozenset({127}), 181)]

在上述这些规则中，第一部分（frozenset）是作为规则前提的电影编号，后面的数字表示作为结论的电影编号。第一组数据表示如果用户喜欢电影79，他很可能喜欢电影258。

接下来，计算每条规则的置信度，计算方法跟第1章类似，只不过要根据这里新的数据格式做些改动。

我们需要先创建两个字典，用来存储规则应验（正例）和规则不适用（反例）的次数。代码如下：

correct_counts = defaultdict(int)
incorrect_counts = defaultdict(int)

遍历所有用户及其喜欢的电影数据，在这个过程中遍历每条关联规则。

for user, reviews in favorable_reviews_by_users.items():
    for candidate_rule in candidate_rules:
        premise, conclusion = candidate_rule

测试每条规则的前提对用户是否适用。换句话说，用户是否喜欢前提中的所有电影。代码如下：

        if premise.issubset(reviews):

如果前提符合，看一下用户是否喜欢结论中的电影。如果是的话，规则适用，反之，规则不适用。

        if premise.issubset(reviews):
            if conclusion in reviews:
                correct_counts[candidate_rule] += 1
            else:
                incorrect_counts[candidate_rule] += 1

用规则应验的次数除以前提条件出现的总次数，计算每条规则的置信度。

rule_confidence = {candidate_rule: correct_counts[candidate_rule]
  / float(correct_counts[candidate_rule] +
    incorrect_counts[candidate_rule])
              for candidate_rule in candidate_rules}

对置信度字典进行排序后，输出置信度最高的前五条规则。

from operator import itemgetter
sorted_confidence = sorted(rule_confidence.items(),
  key=itemgetter(1), reverse=True)
for index in range(5):
    print("Rule #{0}".format(index + 1))
    (premise, conclusion) = sorted_confidence[index][0]
    print("Rule: If a person recommends {0} they will also
      recommend {1}".format(premise, conclusion))
    print(" - Confidence:
      {0:.3f}".format(rule_confidence[(premise, conclusion)]))
    print("")

结果如下：

Rule #1
Rule: If a person recommends frozenset({64, 56, 98, 50, 7}) they will
also recommend 174
 - Confidence: 1.000
Rule #2
Rule: If a person recommends frozenset({98, 100, 172, 79, 50, 56})
they will also recommend 7
 - Confidence: 1.000
Rule #3
Rule: If a person recommends frozenset({98, 172, 181, 174, 7}) they
will also recommend 50
 - Confidence: 1.000
Rule #4
Rule: If a person recommends frozenset({64, 98, 100, 7, 172, 50}) they
will also recommend 174
 - Confidence: 1.000
Rule #5
Rule: If a person recommends frozenset({64, 1, 7, 172, 79, 50}) they
will also recommend 181
 - Confidence: 1.000

输出结果中只显示电影编号，而没有显示电影名字，很不友好。我们下载的数据集中的u.items文件里存储了电影名称和编号（还有体裁等信息）。

用pandas从u.items文件加载电影名称信息。关于该文件和类别的更多信息请见数据集中的README文件。u.items文件为CSV格式，但是用竖线分隔数据。读取时需要指定分隔符，设置表头和编码格式。每一列的名称是从README文件中找到的。

movie_name_filename = os.path.join(data_folder, "u.item")
movie_name_data = pd.read_csv(movie_name_filename, delimiter="|",
  header=None, encoding = "mac-roman")
movie_name_data.columns = ["MovieID", "Title", "Release Date",
  "Video Release", "IMDB", "<UNK>", "Action", "Adventure",
    "Animation", "Children's", "Comedy", "Crime", "Documentary",
      "Drama", "Fantasy", "Film-Noir",
  "Horror", "Musical", "Mystery", "Romance", "Sci-Fi", "Thriller",
    "War", "Western"]

既然电影名称对于理解数据很重要，我们就来创建一个用电影编号获取名称的函数，以免去每次都要人工查找的烦恼。函数声明如下：

def get_movie_name(movie_id):

在数据框movie_name_data中查找电影编号，找到后，只返回电影名称列的数据。

    title_object = movie_name_data[movie_name_data["MovieID"] ==
      movie_id]["Title"]

我们用title_object的values属性获取电影名称（不是存储在title_object中的Series对象）。我们只对第一个值感兴趣——当然每个电影编号只对应一个名称！

    title = title_object.values[0]

函数最后返回电影名称。

    return title

调整之前的代码，这样就能在输出的规则中显示电影名称。请在IPython Notebook笔记本文件的新格子里输入以下代码。

for index in range(5):
    print("Rule #{0}".format(index + 1))
    (premise, conclusion) = sorted_confidence[index][0]
    premise_names = ", ".join(get_movie_name(idx) for idx
      in premise)
    conclusion_name = get_movie_name(conclusion)
    print("Rule: If a person recommends {0} they will
      also recommend {1}".format(premise_names, conclusion_name))
    print(" - Confidence: {0:.3f}".format(confidence[(premise,
      conclusion)]))
print("")

结果清楚多了（还有些小问题，暂时先忽略）。

Rule #1
Rule: If a person recommends Shawshank Redemption, The (1994), Pulp
Fiction (1994), Silence of the Lambs, The (1991), Star Wars (1977),
Twelve Monkeys (1995) they will also recommend Raiders of the Lost Ark
(1981)
 - Confidence: 1.000
Rule #2
Rule: If a person recommends Silence of the Lambs, The (1991), Fargo
(1996), Empire Strikes Back, The (1980), Fugitive, The (1993), Star
Wars (1977), Pulp Fiction (1994) they will also recommend Twelve
Monkeys (1995)
 - Confidence: 1.000
Rule #3
Rule: If a person recommends Silence of the Lambs, The (1991), Empire
Strikes Back, The (1980), Return of the Jedi (1983), Raiders of the
Lost Ark (1981), Twelve Monkeys (1995) they will also recommend Star
Wars (1977)
 - Confidence: 1.000
Rule #4
Rule: If a person recommends Shawshank Redemption, The (1994), Silence
of the Lambs, The (1991), Fargo (1996), Twelve Monkeys (1995), Empire
Strikes Back, The (1980), Star Wars (1977) they will also recommend
Raiders of the Lost Ark (1981)
 - Confidence: 1.000
Rule #5
Rule: If a person recommends Shawshank Redemption, The (1994), Toy
Story (1995), Twelve Monkeys (1995), Empire Strikes Back, The (1980),
Fugitive, The (1993), Star Wars (1977) they will also recommend Return
of the Jedi (1983)
 - Confidence: 1.000

评估

广义上讲，我们可以拿评估分类算法的那一套来用。训练前，留出一部分数据用于测试，评估发现的规则在测试集上的表现。

如果这样做的话，我们就需要计算每条规则在测试集中的置信度。

这里我们不打算用正式的评价指标，只是简单看一下每条规则的表现，寻找好的规则。

首先，抽取所有没有用于训练的数据作为测试集。训练集用前200名用户的打分数据，测试集就用剩下的数据。就训练集来说，我们会为该数据集中的每一位用户获取最喜欢的电影。代码如下：

test_dataset =
all_ratings[~all_ratings['UserID'].isin(range(200))]
test_favorable = test_dataset[test_dataset["Favorable"]]
test_favorable_by_users = dict((k, frozenset(v.values)) for k, v
  in test_favorable.groupby("UserID")["MovieID"])

接着，计算规则应验的数量，方法跟之前相同。唯一的不同就是这次使用的是测试数据而不是训练数据。代码如下：

correct_counts = defaultdict(int)
incorrect_counts = defaultdict(int)
for user, reviews in test_favorable_by_users.items():
    for candidate_rule in candidate_rules:
        premise, conclusion = candidate_rule
        if premise.issubset(reviews):
            if conclusion in reviews:
                correct_counts[candidate_rule] += 1
            else:
                incorrect_counts[candidate_rule] += 1

接下来，计算所有应验规则的置信度。

test_confidence = {candidate_rule: correct_counts[candidate_rule]
  / float(correct_counts[candidate_rule] + incorrect_counts
    [candidate_rule])
  for candidate_rule in rule_confidence}

最后，输出用电影名称而不是电影编号表示的最佳关联规则。

for index in range(5):
    print("Rule #{0}".format(index + 1))
    (premise, conclusion) = sorted_confidence[index][0]
    premise_names = ", ".join(get_movie_name(idx) for idx in
      premise)
    conclusion_name = get_movie_name(conclusion)
    print("Rule: If a person recommends {0} they will also
      recommend {1}".format(premise_names, conclusion_name))
    print(" - Train Confidence:
      {0:.3f}".format(rule_confidence.get((premise, conclusion),
        -1)))
    print(" - Test Confidence:
     {0:.3f}".format(test_confidence.get((premise, conclusion),
        -1)))
     print("")

我们来看一下在新数据集上哪些规则最适用。

Rule #1
Rule: If a person recommends Shawshank Redemption, The (1994), Pulp
Fiction (1994), Silence of the Lambs, The (1991), Star Wars (1977),
Twelve Monkeys (1995) they will also recommend Raiders of the Lost Ark
(1981)
 - Train Confidence: 1.000
 - Test Confidence: 0.909
Rule #2
Rule: If a person recommends Silence of the Lambs, The (1991), Fargo
(1996), Empire Strikes Back, The (1980), Fugitive, The (1993), Star
Wars (1977), Pulp Fiction (1994) they will also recommend Twelve
Monkeys (1995)
 - Train Confidence: 1.000
 - Test Confidence: 0.609
Rule #3
Rule: If a person recommends Silence of the Lambs, The (1991), Empire
Strikes Back, The (1980), Return of the Jedi (1983), Raiders of the
Lost Ark (1981), Twelve Monkeys (1995) they will also recommend Star
Wars (1977)
 - Train Confidence: 1.000
 - Test Confidence: 0.946
Rule #4
Rule: If a person recommends Shawshank Redemption, The (1994), Silence
of the Lambs, The (1991), Fargo (1996), Twelve Monkeys (1995), Empire
Strikes Back, The (1980), Star Wars (1977) they will also recommend
Raiders of the Lost Ark (1981)
 - Train Confidence: 1.000
 - Test Confidence: 0.971
Rule #5
Rule: If a person recommends Shawshank Redemption, The (1994), Toy
Story (1995), Twelve Monkeys (1995), Empire Strikes Back, The (1980),
Fugitive, The (1993), Star Wars (1977) they will also recommend Return
of the Jedi (1983)
 - Train Confidence: 1.000
 - Test Confidence: 0.900

举例来说，第二条规则，在训练集中置信度为1，但在测试集上正确率只有60%。但前十条规则中，其他几条规则在测试集上置信度也很高，用它们来推荐电影效果不错。

　浏览剩余规则，你可能发现有些规则的置信度为-1。置信度一般为0到1之间的值。负数表示这条规则在测试集中根本不存在。

4.5　小结

本章把亲和性分析用到电影推荐上，从大量电影打分数据中找到可用于电影推荐的关联规则。整个过程分为两大阶段。首先，借助Apriori算法寻找数据中的频繁项集。然后，根据找到的频繁项集，生成关联规则。

由于数据集较大，Apriori算法就很有必要。虽然第1章使用最笨的方法来寻找规则，但是在这里就不适用了，由于时间复杂度呈指数级增长，我们需要寻找更巧妙的解决方案。这种现象在数据挖掘中很常见：虽然可以用最笨的方法穷尽所有情况来解决问题，但在数据量很大的情况下必须要使用更灵活、更快捷的算法。

我们用一部分数据作为训练集以发现关联规则，在剩余数据——测试集上进行测试。可以用前几章的交叉检验方法对每条规则的效果进行更为充分的评估。

到目前为止，我们使用的数据集都有很明显的特征。然而，不是所有数据集都是这个样子。下一章将学习用scikitlearn的转换器（第3章曾介绍过）从数据中抽取特征。还将讨论怎样实现自己的转换器和扩展已有转换器，并介绍相关概念。

第 4 章 用亲和性分析方法推荐电影

第 4 章 用亲和性分析方法推荐电影

4.1 亲和性分析

4.1.1 亲和性分析算法

4.1.2 选择参数

4.2 电影推荐问题

4.2.1 获取数据集

4.2.2 用pandas加载数据

4.2.3 稀疏数据格式

4.3 Apriori算法的实现

4.3.1 Apriori算法

4.3.2 实现

4.4 抽取关联规则

评估

4.5 小结

第 4 章　用亲和性分析方法推荐电影

第 4 章　用亲和性分析方法推荐电影

4.1　亲和性分析

4.1.1　亲和性分析算法

4.1.2　选择参数

4.2　电影推荐问题

4.2.1　获取数据集

4.2.2　用pandas加载数据

4.2.3　稀疏数据格式

4.3　Apriori算法的实现

4.3.1　Apriori算法

4.3.2　实现

4.4　抽取关联规则

4.5　小结