第3章　量子黑洞

史蒂芬·霍金

我准备在我第二次讲演中谈论黑洞的量子理论。它似乎在物理学中导致一种在新的水平上的不可预见性，这种不可预见性超越于和量子力学相关的通常的不确定性之上。这是因为发现黑洞具有内禀的熵，而且引起信息从我们的宇宙区域消失。我应该说，这些断言是富有争议的：许多量子引力的研究者，几乎包括所有从粒子物理转行的人，都本能地拒绝这种思想，即有关一个系统量子态的信息会丧失掉。然而，他们在显示信息何以能从黑洞取出方面徒劳无功。我最终相信，他们将被迫接受我的建议，信息是丧失掉了，正如他们过去被迫同意黑洞辐射一样，这和他们的先验观念互相抵触。

我必须首先提醒你们有关黑洞的经典理论。我们从上次讲演得知，至少在正常的情形下引力总是吸引的。如果引力像电动力学那样，时而吸引时而排斥，我们就永远不会觉察到它，因为它大约比电磁力微弱10⁴⁰倍。正是由于引力总是同号，才使得像我们和地球这样的两个宏观物体中的粒子之间的引力叠加起来，得到我们能感觉得到的力量。

引力是吸引的这个事实意味着，它要把宇宙中的物质赶到一起形成例如恒星和星系这样的物体。在一段时间内，恒星可由热压力，星系可由旋转以及内部运动来支撑自己，避免进一步收缩。然而，热和角动量最终会被抽走，物体就开始收缩。如果质量比太阳的一倍半左右还小，电子或者中子的简并压力就能阻止它收缩。该物体就会分别以白矮星或者中子星作为归宿。然而，如果质量比这个极限还大，则没有任何办法可以支撑它并阻止它继续收缩。一旦它缩小到某一临界的尺度，它表面上的引力场会变得这么强，甚至连光锥都向里弯折，正如图3.1所示的。我是想过为你画一张四维图。然而，政府经费的缩减使剑桥大学只能提供得起两维的屏幕。因此，我把时间标在垂直方向，并且利用透视法把三维空间中的两维标出来。你可以看到，甚至连外向的光线也被相互向内地弯折了，它变成收敛的而不是发散的了。这表明存在一个闭合的捕获面，这正是霍金—彭罗斯定理的第三个条件中的一种情形。

如要宇宙监督猜想是正确的，则捕获面和它所预言的奇性不能在远处被看到。这样，在时空中就有这样的一个区域，不可能从那儿逃逸到无穷远去。正如我们在上次讲演中得知的，事件视界的截面积永远不会减小，至少在经典理论中情形应是如此。这些以及球形坍缩的微扰计算暗示，黑洞将会以一种稳恒态为归宿。由伊斯雷尔、卡特、罗宾逊以及我自己共同努力所证明的无毛定理指出，在没有物质场时克尔解是仅有的稳恒黑洞。它们由两个参数所表征，即质量M和角动量J。罗宾逊把无毛定理推广到电磁场存在的情形。这就加上了第三个参数Q，也就是电荷。对于杨—米尔斯场，无毛定理还未被证明，但是仅有的区别似乎是要加上作为不稳定解的分立族指标的一个或多个整数。可以证明与时间无关的爱因斯坦—杨—米尔斯黑洞不会再有更多的连续自由度。

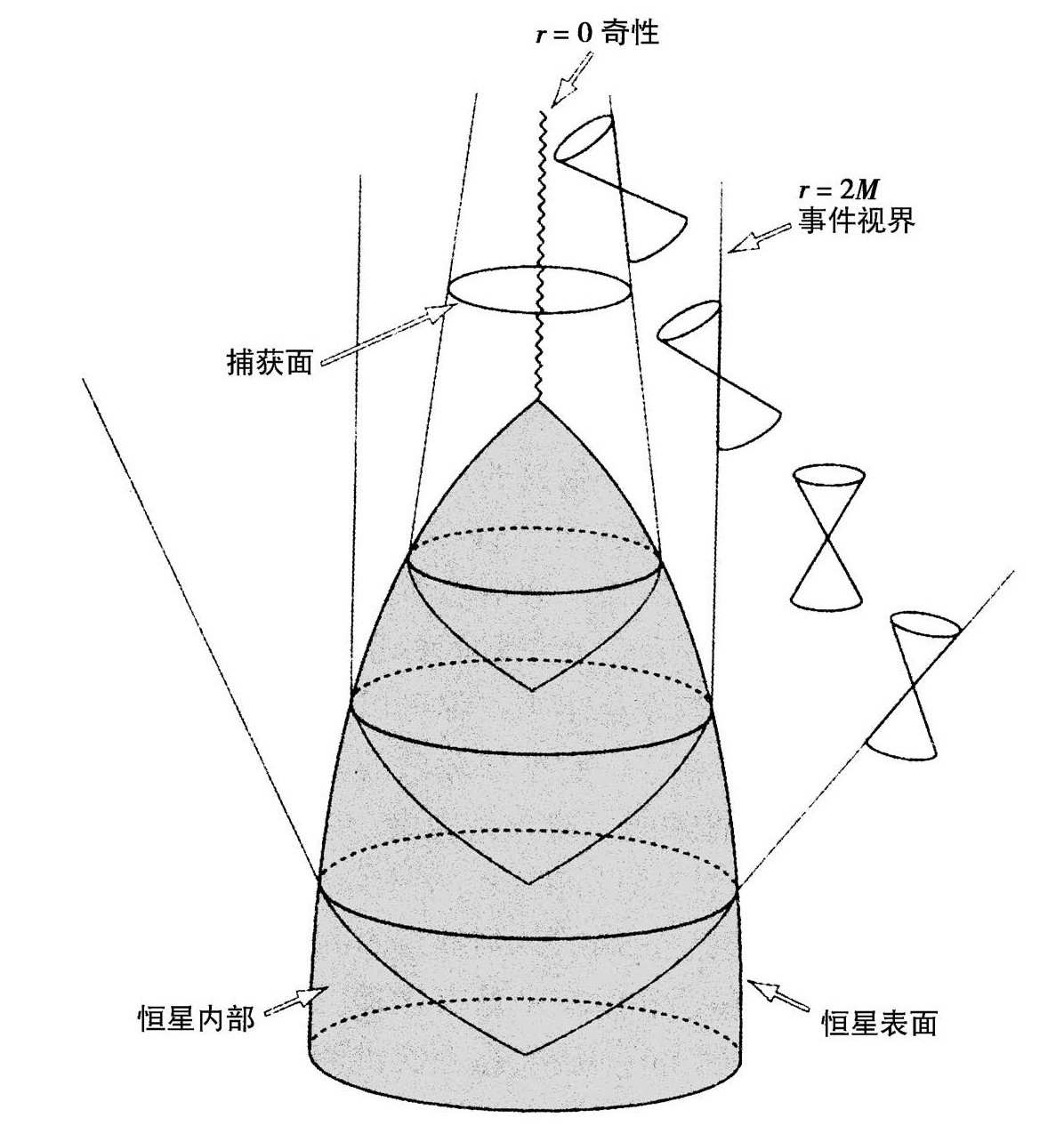
图3.1　一个恒星坍缩形成黑洞的时空图，图上标出事件视界和闭合捕获面

无毛定理指出，当一个物体坍缩形成黑洞时，大量信息丧失了。坍缩物体要用大量参数才能描述。其中有物质的类型以及物体分布的多极矩。可是形成的黑洞和物质类型完全无关，而且除了最先的两个极矩外，其他的所有多极矩迅速丧失。这两个极矩便是：质量和二极矩，也就是角动量。

无毛定理：稳态黑洞是用质量M，角动量J，以及电荷Q来表征。

信息丧失在经典理论中没有什么关系。人们可以说，有关坍缩物体的全部信息仍然藏在黑洞之中。一位外在于黑洞的观察者去确定以前的坍缩物体是什么将是非常困难的。然而，这在经典理论中在原则上仍然是可能的。观察者实际上将永远看得见坍缩物体。它会显得越来越迟缓，在它接近事件视界时变得非常黯淡。但是观察者仍然能看到它是什么组成的以及物质如何分布。然而，量子理论把这一切都改变了。首先，坍缩物体在它穿越事件视界之前只发射出有限数目的光子。要把关于坍缩物体的信息都携带上，这是十分不够的。这意味着，在量子理论中，外界观察者根本无法测量坍缩物体的状态。人们也许会认为这无关紧要，因为尽管从外面测量不到信息，它仍然被保存在黑洞之中。但是正在此处量子理论对黑洞的第二个效应出现了。正如我要指出的，量子理论使黑洞辐射并且丧失质量。看来它们最终会完全消失，和它一道消失的还有在它们当中的信息。我将要论断，这个信息的确是丧失掉了，而且不能以某种方式得到恢复。正像我要指出的，这种信息丧失给物理学引进了新水平的不确定性，这种不确定性是超越于和量子理论相关的通常的不确定性之上。可惜的是，和海森伯不确定性原理不同，这种额外水平的不确定性在黑洞情形下很难被实验所证实。但是正如我将在第三次讲演（第5章）中论断的，在某种意义上，我们已经在测量微波背景起伏中观察到这种效应。

在由坍缩形成的黑洞的背景上做量子场论研究时，首次发现了量子论引起黑洞辐射的事实。利用通常称作彭罗斯图的工具有助于看清这是如何发生的。然而，我以为彭罗斯本人会同意，它们更应该称作卡特图，因为卡特首先系统地使用它们。在球形坍缩中，时空和角度θ和φ无关。所有的几何都在t-r平面上发生。因为任何二维面都和平空间相共形，所以人们可以用一张图来代表因果性结构，在图中r-t平面中的零性线是和垂直方向成±45°的角度。

我们从平坦的闵可夫斯基空间开始，其卡特—彭罗斯图是一个立在一个顶点上的三角形（图3.2）。处于右边的两条斜边对应于我在第一次讲演中提到的过去和未来零性无穷。它们真正是处于无穷远处，但是当接近过去或者未来无穷时所有距离都由共形因子所缩小。这个三角形中的每一点都对应于半径为r的二维球。左边的垂直线r=0代表对称中心，而在图的右边r→∞。

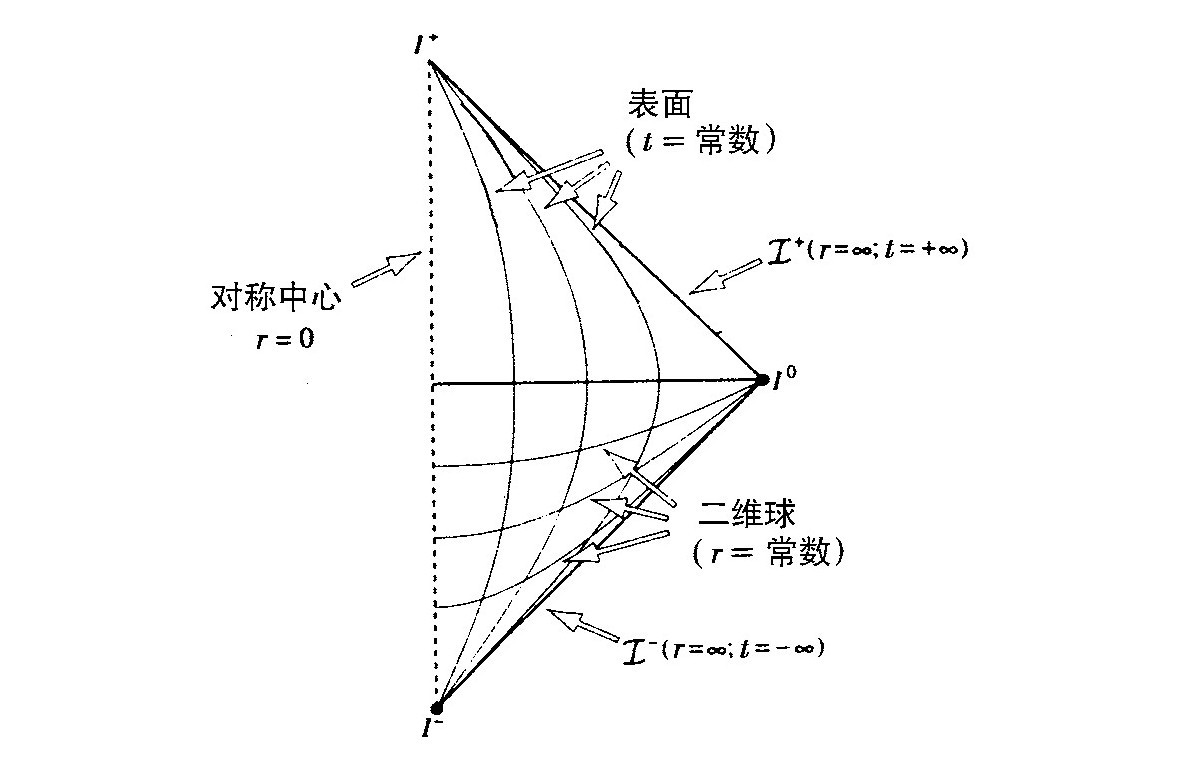
图3.2

闵可夫斯基空间的卡特—彭罗斯图

人们从图上可以很容易看到，闵可夫斯基空间中的每一点都是在未来零性无穷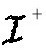的过去中。这表明不存在黑洞和事件视界。然而发生球对称物体坍缩的话，图就相当不一样了（图3.3）。它在过去看起来是相同的，但是现在三角形的顶被切去了，而且用一个水平的边界来取代。这便是霍金—彭罗斯定理所预言的奇性。现在人们可以看到，在这根水平线之下有些点不是处于未来零性无穷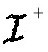的过去。换句话说，存在有黑洞。其事件视界，也就是黑洞边界是从右上角下来的斜线，并和对应于对称中心的垂直线相交。

人们可以在此背景中考虑一个标量场。如果时空是与时间无关的，则在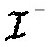只包含正频率的波动方程的解，在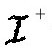也具有正频率。这就表明没有粒子产生，而且如果原先没有标量粒子的话，则在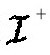处不会有向外飞行的粒子。

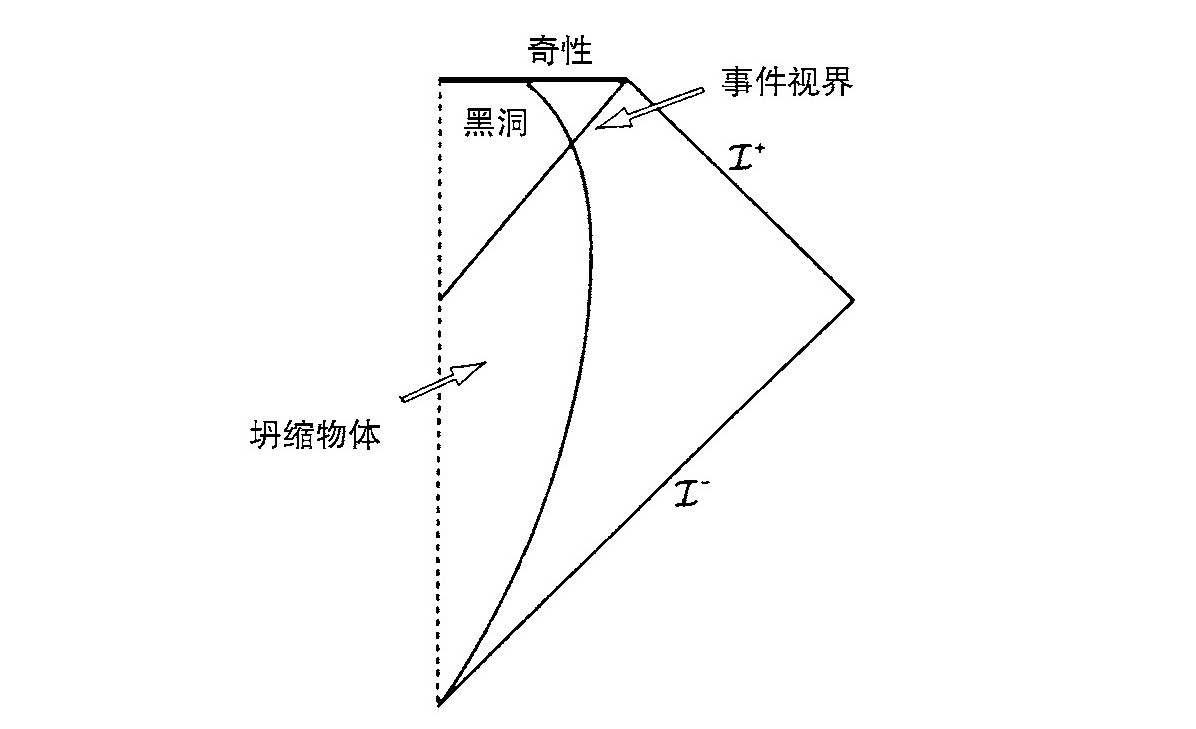
图3.3　一颗恒星坍缩形成黑洞的卡特—彭罗斯图

然而，在坍缩之际度规与时间相关。这就导致在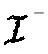处是正频率的一个解到达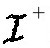时部分地变成负频率的。人们可以首先取一个在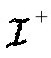处具有时间依赖e^-iωµ的波，让它往回传播到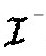，用这种办法来计算这种混合。当人们这么做时，他们会发现通过接近视界的部分波被大大地蓝移了。令人印象深刻的是，人们发现，在晚期的极限，其混合与坍缩的细节无关。它只依赖于表面引力k，这是黑洞视界上引力场强度的测度。正、负频率的混合导致粒子产生。

当我于1973年首次研究这个效应时，我预料到会发现在坍缩时的一次辐射暴，但是之后粒子不再产生，最后余下的是一个真正黑的黑洞。使我大为惊讶的是，我发现在坍缩时的一次辐射暴后仍然维持着粒子产生和发射的稳恒的速率。此外，这种辐射具有温度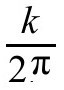，是准确的热性的。这正是使黑洞具有和它事件视界面积成比例的熵的观念协调所亟需的东西。它还把该比例常数确定为在普朗克单位下的四分之一，在普朗克单位中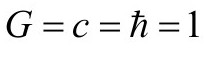。普朗克单位的面积是10^-66平方厘米，这样具有太阳质量的黑洞具有数量级为10⁷⁸的熵。这反映了可能制造该黑洞的极其巨大数目的不同方式。

黑洞热辐射

当我首次发现黑洞辐射时，从相当繁乱的计算中导出了完全热性的辐射，这似乎是一桩奇迹。然而，和詹姆·哈特尔以及盖瑞·吉朋斯的合作揭露了深层的原因。为了解释这一点，我要从史瓦西度规出发。

史瓦西度规

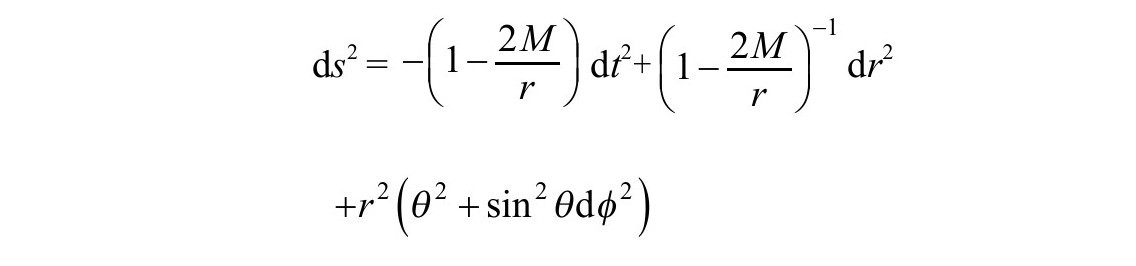
这代表了非旋转的黑洞归宿的引力场。在通常的r和t坐标系中，于史瓦西半径r=2M处有一表观奇性。然而，这只不过是因为坐标选取不好而引起的。人们可以选取其他的坐标使那儿的度规正常。

其卡特—彭罗斯图具有两头被切平的金刚石形状（图3.4）。它被在r=2M的两个零性面分割成四个区域。右边的在图中被标为①的区域是渐近平坦的空间，我们就假定生活在此。正如平坦时空的情形，它具有过去和未来零性无穷。左边还存在另一个渐近平坦区域③，它只能通过一个虫洞和我们的宇宙相连接。然而，正如我们将会看到的，它是通过虚时间和我们的区域相连接。从左下端到右上端的零性面正是我们从那儿能逃逸到在右边的无穷的区域的边界。这样，它是未来事件视界，修饰词未来是用来和从右下端到左上端的过去事件视界相区别。

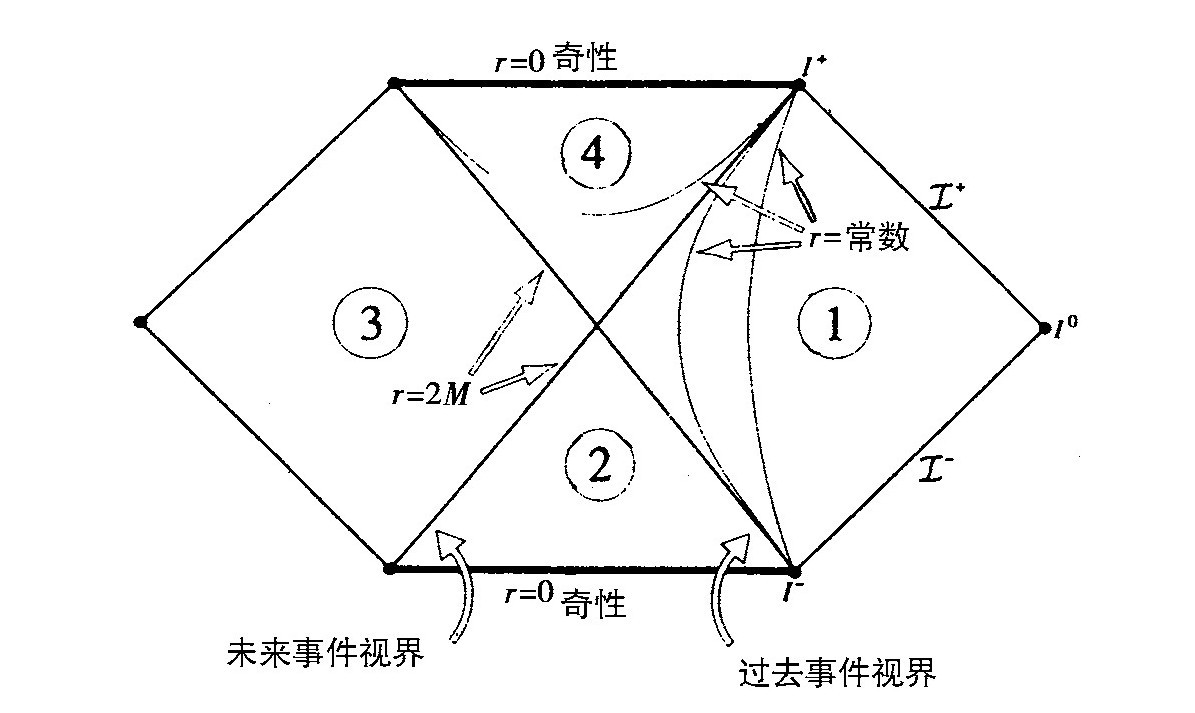
图3.4　永久史瓦西黑洞的卡特—彭罗斯图

让我们回到在原始的r和t坐标中的史瓦西度规上来。如果我们取t=iτ则得到正度规，我把这种正定度规称作欧氏的，尽管它也许是弯曲的。在欧氏史瓦西度规中在r=2M处又有一个表观奇性。然而，人们可以定义一个新的径向坐标

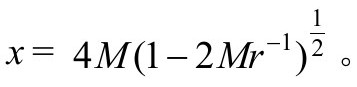
欧氏史瓦西度规

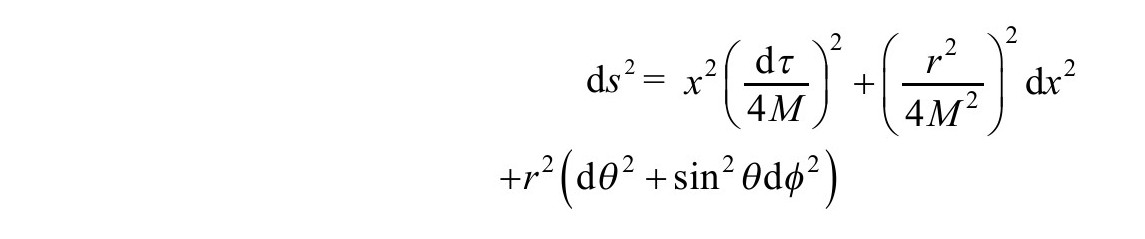
如果人们把坐标τ以周期8πM来相等同，则x-τ平面上的度规就和极坐标的原点相似。类似地，其他欧氏黑洞度规在它们的视界也有表观奇性，只要在虚时间坐标中以周期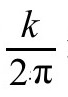来相等同，就能摆脱这种表观奇性（图3.5）。

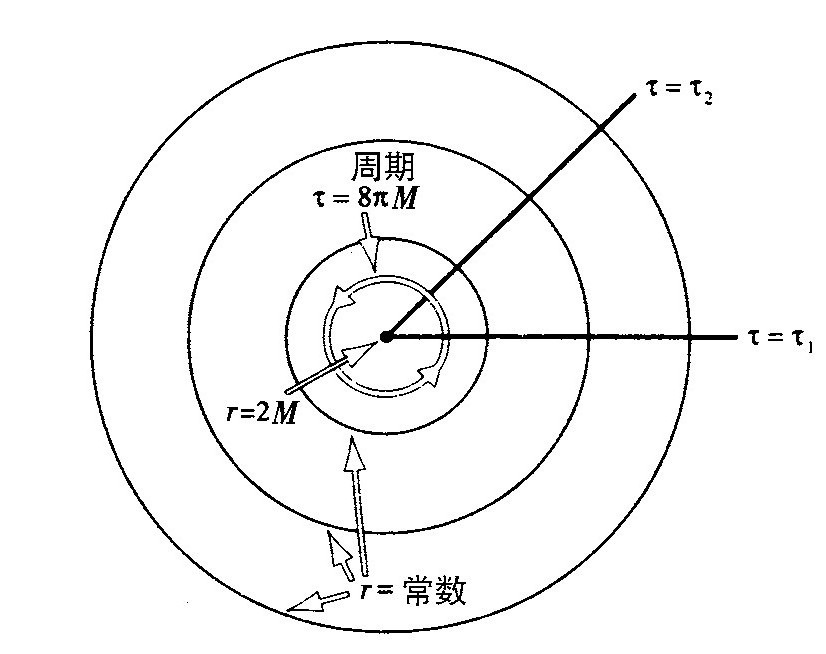
图3.5　欧氏史瓦西解，这里τ被周期性地等同

虚时间以某种周期β相等同的意义是什么呢？为了看到这一点，考虑从面t₁上的场配置φ₁到面t₂上的场配置φ₂的幅度。它可由e^{−iH（t₂−t₁）}的矩阵元得出。然而，人们还可以用一个路径积分来代表这个幅度，这个积分是对在t₁和t₂之间的所有场φ的求和得出，而在两个端面上要求φ和场φ₁以及φ₂相一致（图3.6）。

图3.6　从在t₁时态φ₁到t₂时态φ₂的幅度

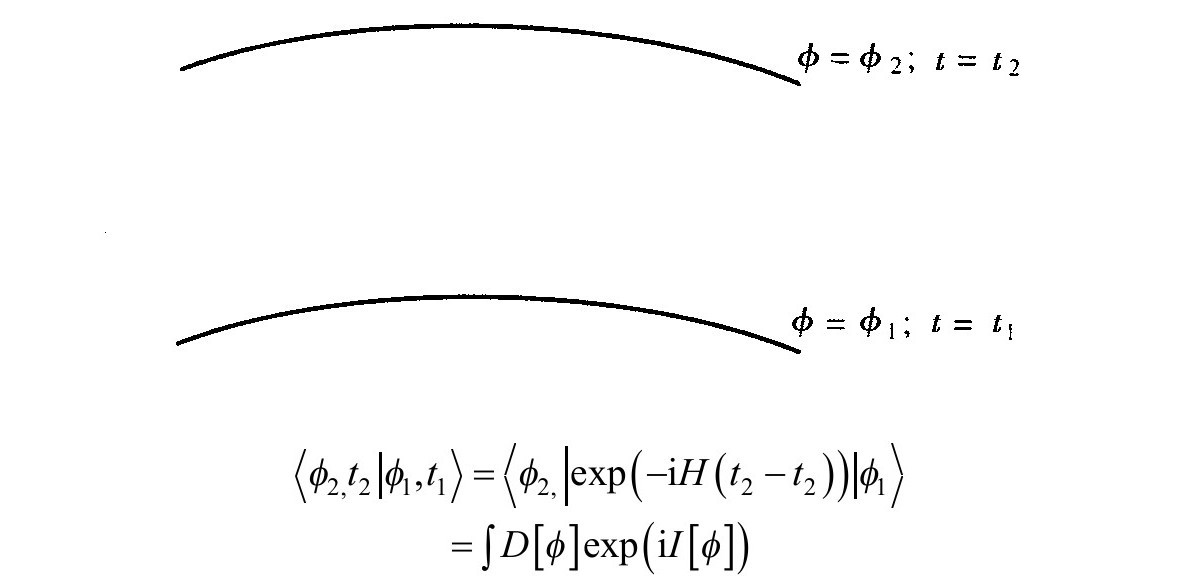
人们现在可以把时间间隔（t₂-t₁）取作虚的，并让它等于β（图3.7）。人们还可以使初始场φ₁和终结场φ₂相同，并对态的完备的基求和。在左边就得到e^-βH对所有态求和的平均值。这正是在温度T=β^-1下的热力学配分函数。

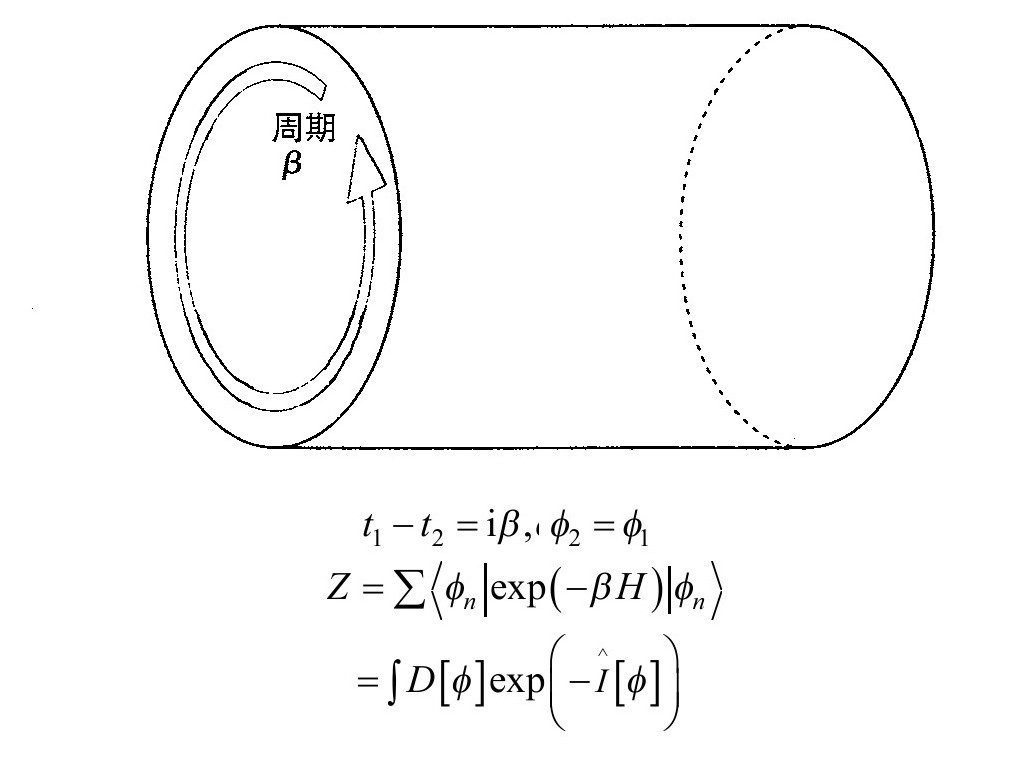
图3.7　对在虚时间方向具有周期β=T^-1的欧氏时空上的所有场求和的路径积分，可以得到温度T下的配分函数

在方程的右边是一个路径积分。人们使φ₁和φ₂相同并对所有的场配置φ_n求和。这表明，实际上是在进行路径积分，是对在虚时间方向以β为周期等同的时空上的所有场求和。这样在温度T下，场φ的配分函数可由对在欧氏时空上的所有场求和的路径积分给出。这个时空在虚时间方向具有周期β=T^-1。

如果人们对在虚时间方向周期β等同的平坦时空上进行路径积分，就会得到黑体辐射的配分函数的通常结果。然而，正如我们刚看到的，欧氏史瓦西解在虚时间方向也具有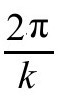的周期。这意味着在史瓦西背景中的场的行为正如同处于具有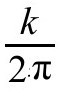温度的热状态中一样。

虚时间的周期性解释了为何频率混合的繁复计算会导致准确的热性的辐射。然而，这个推导避免了参与在频率混合方法中的极高频率的问题。它还可适用于在背景中的相互作用场的情形。在一个周期性背景中进行路径积分意味着，所有物理量，譬如平均值等等，都是热性的。利用频率混合方法可非常困难地得到同样结果。

人们可以把这些相互作用推广到包括引力场自身的相互作用。人们可以从诸如欧氏史瓦西度规的背景度规g₀出发，这种度规是经典场方程的解。然后把作用量I按围绕着g₀的微扰δg的幂次展开：

I[g]=I[g₀]+I₂（δg）²+I₃（δg）³+…

由于背景是场方程的解，所以线性项不出现。平方项可以认为是用来描述背景中的引力子，而立方项以及更高项描述引力子之间的相互作用。对于平方项的路径积分是有限的。纯粹引力在双圈水平上是重正化发散的，但是在超引力理论中它会和费米子相对消。因为还没有人足够勇敢或愚勇地进行过计算，所以还不知道超引力理论在三圈或更多圈水平上是否发散。最近的一些工作显示，也许它们在任意高阶都是有限的。但是，即便在更高阶发散，除了当背景在普朗克长度10^-33厘米的尺度下变曲情形之外，其效应是微不足道的。

零阶项比高阶项更有趣，这也就是背景度规g₀的作用量：

广义相对论的通常的爱因斯坦—希尔伯特作用量是曲率标量R的体积分。对于真空解它为零，这样人们会以为欧氏史瓦西解的作用量为零。然而，在作用量中还有一个表面项，它和边界面的第二基本形式的迹K的积分成比例。当人们把这一项包括进去，并减去平空间的边界项，就会发现欧氏史瓦西度规的作用量为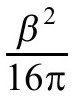，这儿β是在无穷处的虚时间周期。这样，对配分函数Z的路径积分的最重要贡献是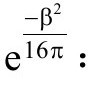

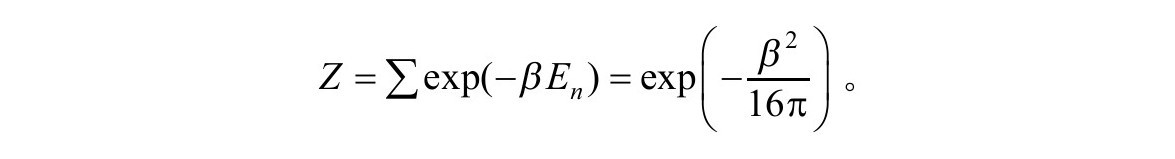
如果取lg Z对周期β的微分，就得到能量，或者质量的平均值：

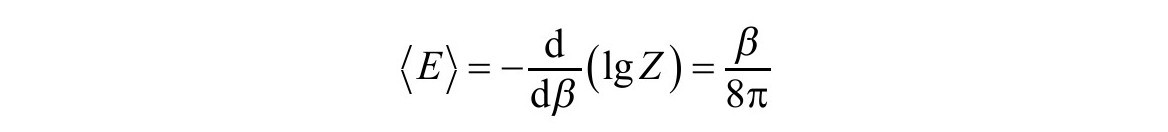
这就得到质量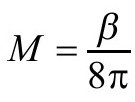。这就证实了质量和周期，或者是温度倒数的关系，这是我们已经知道的。然而，人们可以走得更远。按照标准的热力学论证，配分函数的对数等于负的自由能除以温度

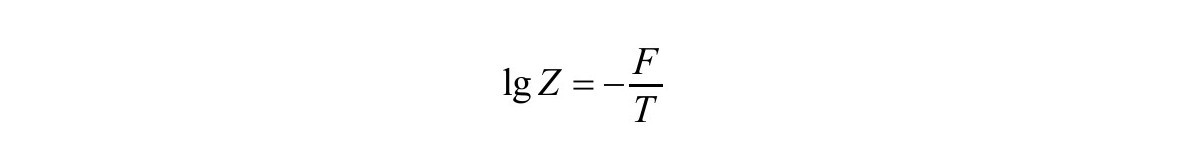
而自由能是质量或能量加上温度乘以熵S：

F=〈E〉+TS。

把这一切合并起来就能看出，黑洞的作用量给出了4πM²的熵：

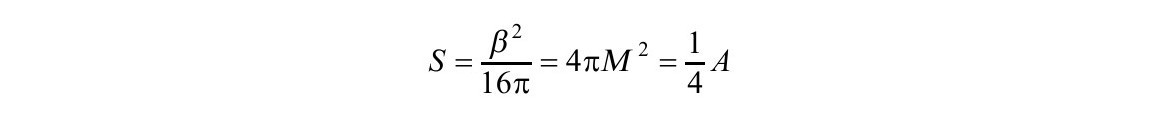
这刚好使黑洞定律和热力学定律相同。

为什么人们能得到这种内禀引力熵，而在其他的量子场论中找不到它的对应物呢？其原因是引力允许时空流形具有不同的拓扑。在我们考虑的情形下，欧氏史瓦西解在无穷具有一个拓扑为S²×S¹的边界。S²是在无穷的巨大的类空二维球，而S¹对应于虚时间方向，它被周期性地等同（图3.8）。人们至少可以在此边界内用两种不同拓扑的度规来填充。其中一个当然是欧氏史瓦西度规。它具有R²×S²的拓扑，也就是欧氏二维平面乘上二维球。另一个是R³×S¹，欧氏平空间在虚时间方面周期等同的拓扑。这两种拓扑具有不同的欧拉数。周期等同平空间欧拉数为零，而欧氏史瓦西解的欧拉数为二。其意义如下所述：在周期等同平空间的拓扑上，人们可以找到一个周期性时间函数τ，其梯度处不为零，并且它和在无穷处的边界上的虚时间坐标相符。然后可以算出在两个面τ₁和τ₂之间区域的作用量。对作用量有两个贡献，一个是对物质拉氏量加上爱因斯坦—希尔伯特拉氏量的体积分，另外一个是表面项。如果解是时间无关的，则在τ=τ₁处的表面项就和在τ=τ₂处的相抵消。这样，在无穷的边界是仅有的对表面项有贡献之处。得到的表面项是质量和虚时间间隔乘积的一半。如果质量不为零，则必须存在产生该质量的非零物质场。可以证明物质拉氏量加上爱因斯坦—希尔伯特拉氏量的体积分也得出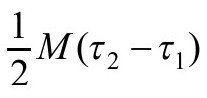。这样总作用量是M（τ₂−τ₁）（图3.9）。如果把这个对配分函数对数的贡献代入热力学公式，就会发现能量平均值为质量，正如所预期的。然而，背景场对熵的贡献是零。

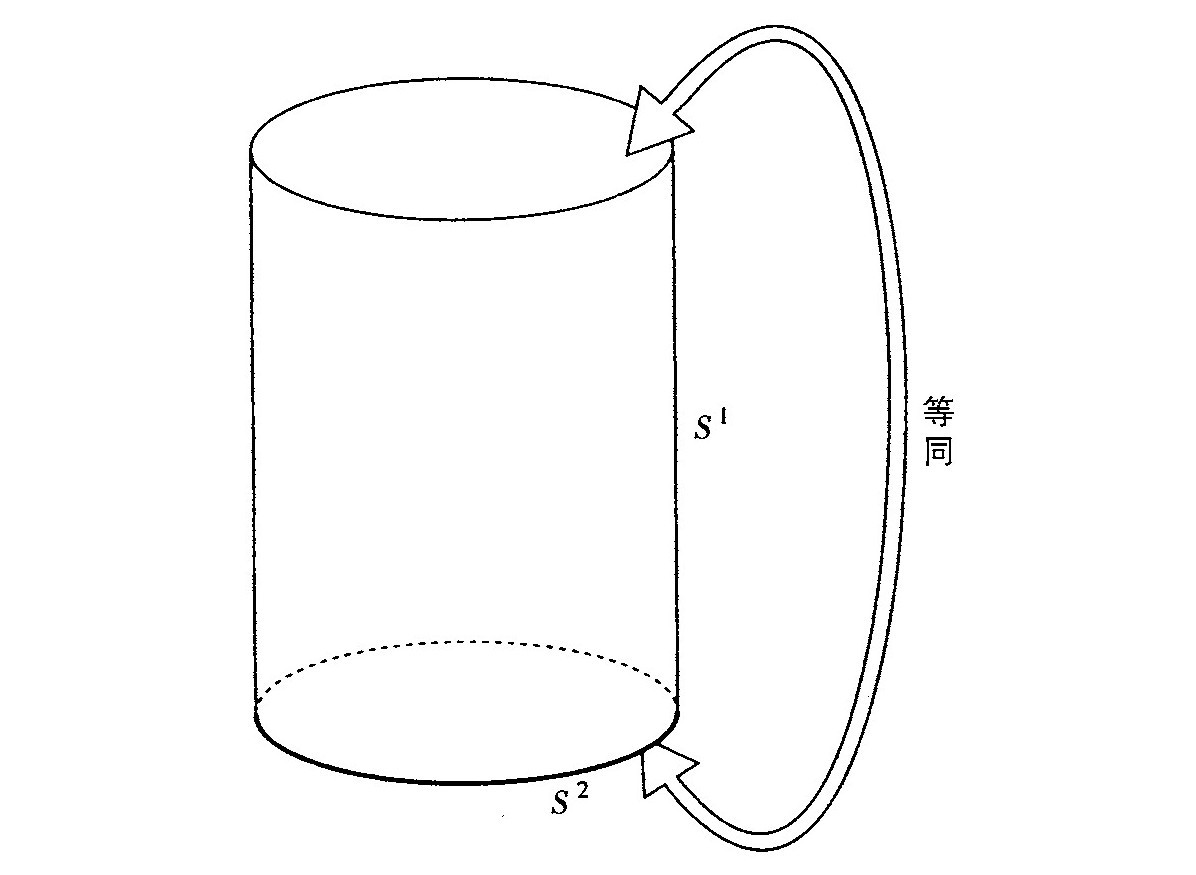
图3.8　欧氏史瓦西解在无穷处的边界

然而，对于欧氏史瓦西解情况就不同了。因为欧拉数为二而不是零，人们就找不到一个其梯度处处不为零的时间函数τ。人们充其量只能选取史瓦西解的虚时间坐标。如果算出两个常数τ表面之间的作用量，由于没有物质场以及曲率标量为零，其体积分为零。而在无穷的迹K的表面项又是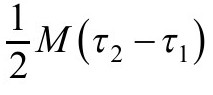。然而，现在在视界处还有另一个表面项，视界便是τ₁和τ₂表面在一个角落相遇之处。人们可以对此表面项求值，发现它又等于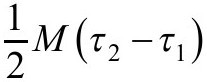（图3.10）。这样，在τ₁和τ₂之间区域的总作用量为M（τ₂-τ₁）。如果人们利用这个作用量并且设τ₂-τ₁=β，就会发现熵为零。然而，如果我们从四维而不是3+1维的观点看待欧氏史瓦西解的作用量，由于度规在视界处是规则的，就没有理由把该处的表面项包括进去。排除视界处的表面项相当于作用量被减小了视界面积的四分之一，这刚好是黑洞的内禀引力熵。

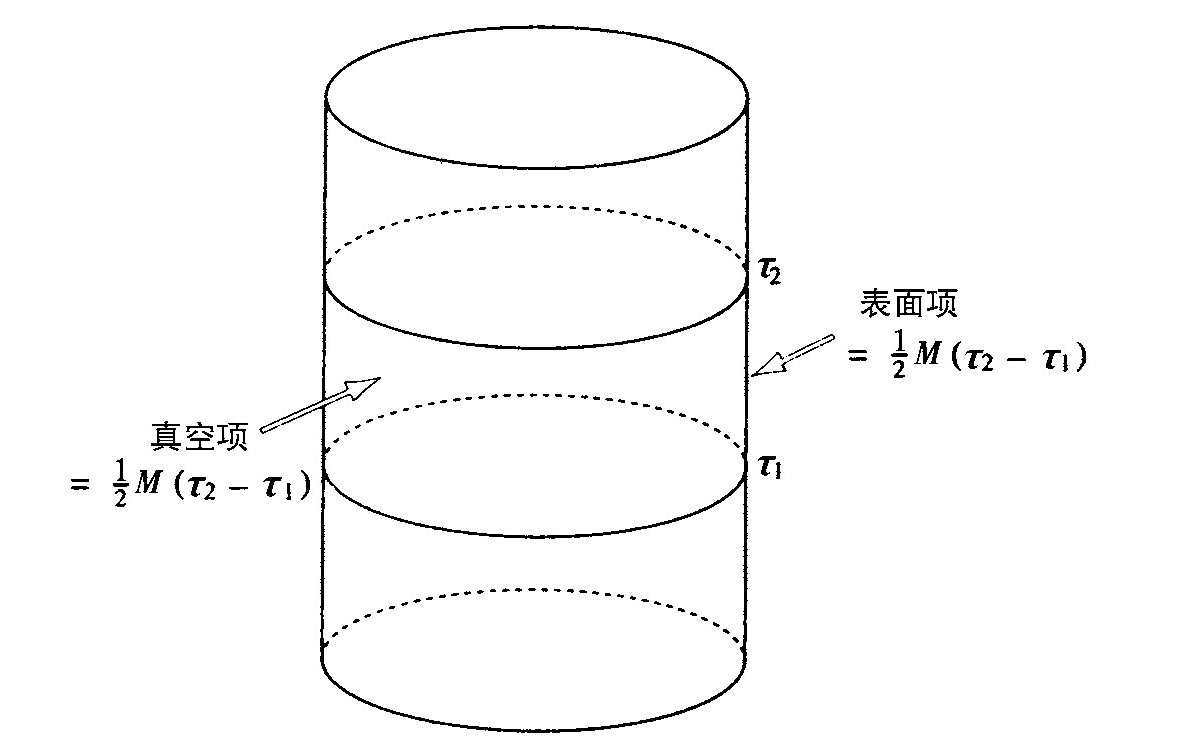
图3.9　周期等同欧氏平空间的作用量=M（τ₂-τ₁）

黑洞熵和拓扑不变量亦即欧拉数相关联的这一事实，是一桩非常强的论断，即便我们必须进入更基本的理论，这个论断仍然有效。对于大多数粒子物理学家而言，这一观念无异为一道诅咒，他们是一大批极端保存者，要把一切都弄得像杨—米尔斯理论。他们赞成，如果黑洞比普朗克长度更大，则黑洞发出的辐射似乎是热性的，而不管它是如何形成的。但是他们也许会声称，随着黑洞损失质量而缩小到普朗克尺度，量子广义相对论就会失效，一切都化为乌有。然而，我将描述一个黑洞的理想实验，信息在黑洞中看来是丧失了，而在视界外时空总是维持着很小的曲率。

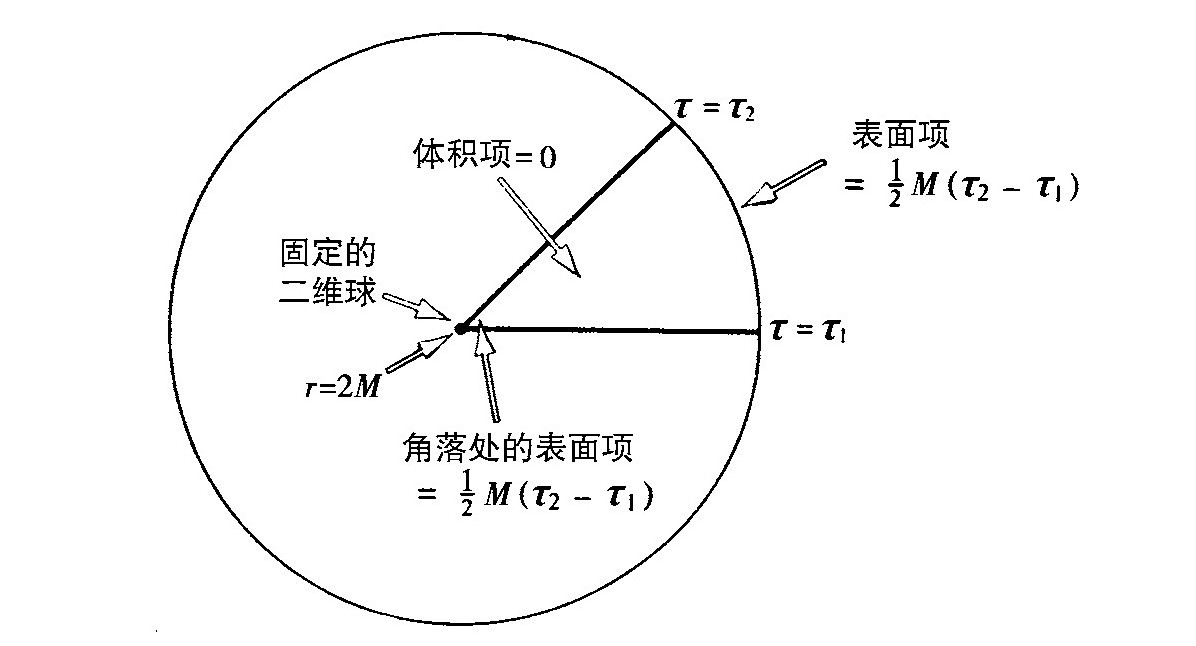
包括角落贡献的总作用量=M（τ₂-τ₁）

排除角落贡献的总作用量=1/2M（τ₂-τ₁）

图3.10　由于我们没有把在r=2M角落处的贡献包括进来，欧氏史瓦西解的总作用量为1/2M（τ₂-τ₁）

一个强电场中能产生带正、负电荷的粒子对，人们知道这个事实已有相当长的时间了。一种看待这个现象的办法是注意到，一个具有电荷q的诸如电子的粒子在平坦的具有均匀电场E的欧氏空间中的运动轨道是一个圆周。人们可以把这个运动从虚时间τ向实时间t做解析连续。他就会得到一对带正、负电的粒子，由于电场的拉力被相互分开而加速飞离（图3.11）。

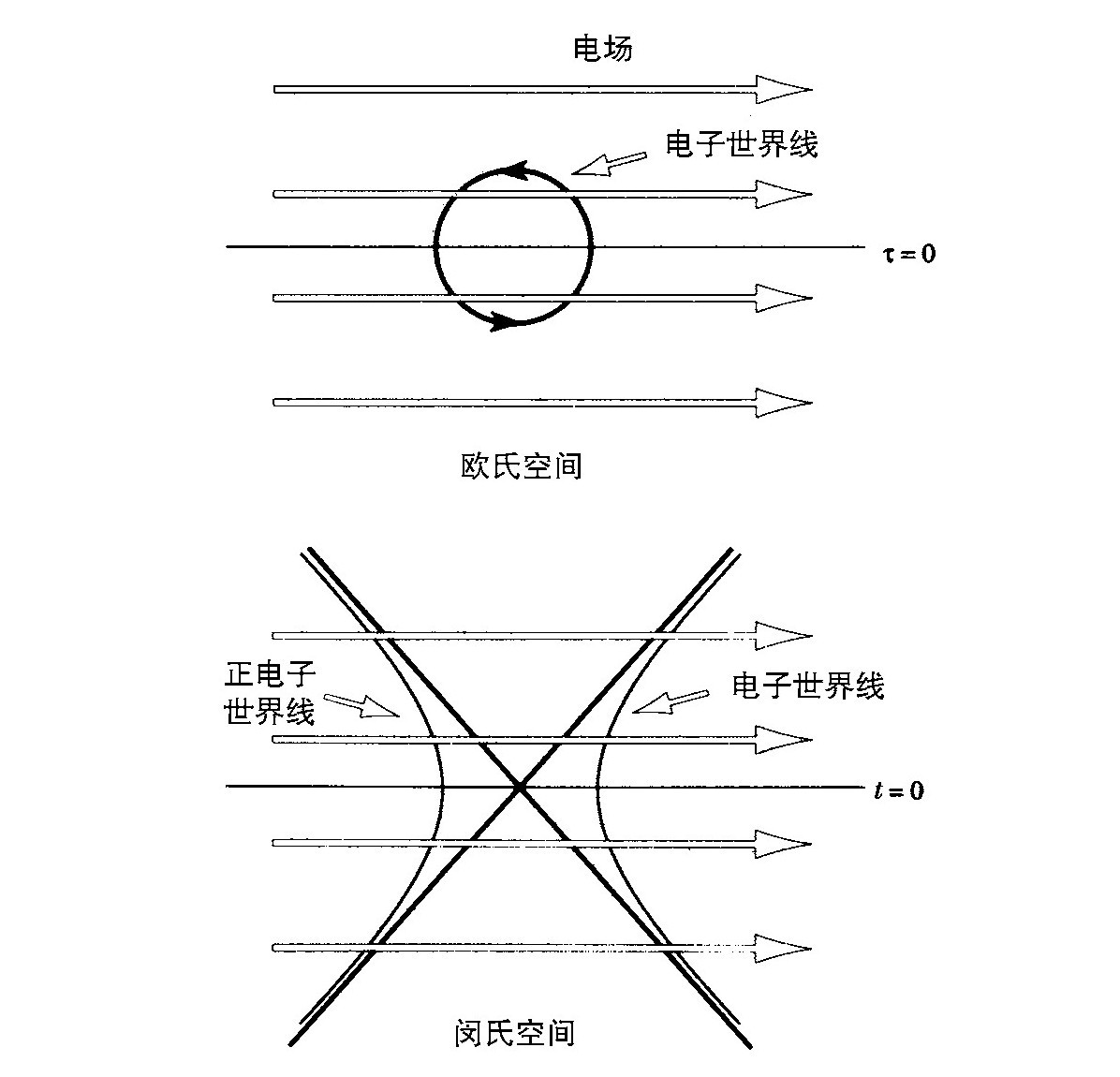
图3.11　在欧氏空间中，一个电子在电场中沿着圆周运动。在闵氏空间中，我们得到一对带反号电荷的粒子，相互加速飞离

对产生的过程可由把两张图沿着t=0或τ=0的线切断来描述。然后把闵氏空间图的上一半和欧氏空间图的下一半接起来（图3.12）。从这个图像中可以看出带正电和带负电的粒子其实是同一粒子。从一个闵可夫斯基世界线过渡到另一个是通过欧几里得空间的隧道穿透的。对产生概率的第一阶近似是e^-I，此处

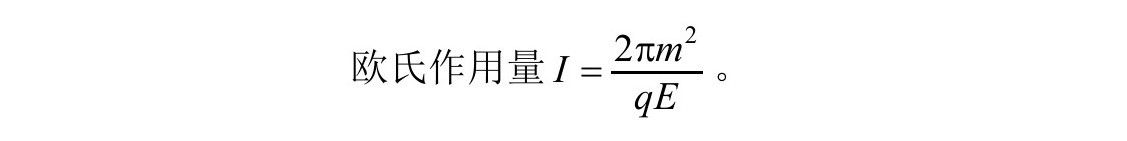
人们已经在实验中观察到强电场对产生，其产生率和这些估计相一致。

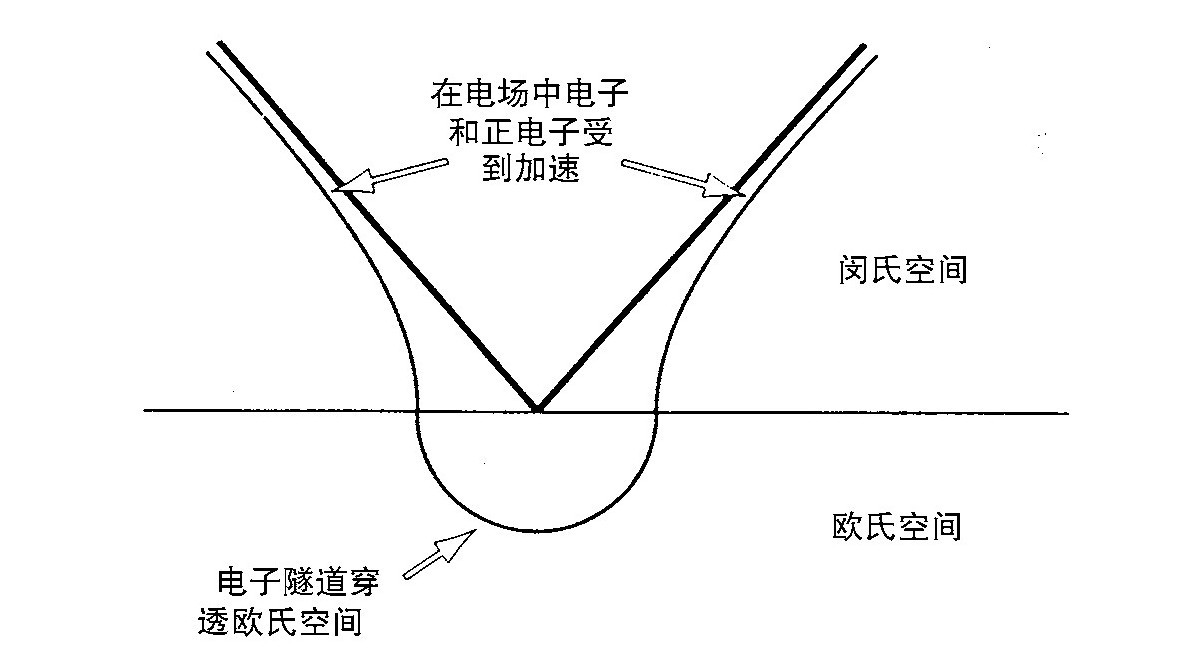
图3.12　可以利用半张欧氏图和半张闵氏图的连接来描述对产生

由于黑洞也能带电荷，所以人们预料，它们也可以成对地产生。然而，因为黑洞的质荷比大了10²⁰倍，所以产生率和电子—正电子对相比就显得非常微小。这表明在产生黑洞对的概率达到可观的数值之前，电子—正电子对产生早已把任何电场中和了。然而，还有一些带有磁荷的黑洞解。因为不存在带磁荷的基本粒子，所以这类黑洞不能由引力坍缩产生。但是人们可以预料，它们可以在一强磁场中成对地产生。因此，磁场可以强到足以使带磁荷的黑洞对产生的概率相当可观。

1976年恩斯特找到了一个代表在磁场中的两个带磁荷的相互加速离开的黑洞的解（图3.13）。黑洞在弯曲的欧氏空间沿着一个圆周运动，正如同在平坦的欧氏空间电子沿着一个圆周运动一样（图3.14）。因为虚时间不仅在围绕黑洞的视界而且在围绕黑洞运动的圆周的中心都是周期性的，所以引起了复杂性。人们必须调整黑洞质荷比使这两个周期相同。在物理学上，这表明人们应这样选取黑洞的参数，使得黑洞的温度和由于加速而呈现的温度相等。随着磁荷趋近于在普朗克单位下的质量，黑洞的温度趋近于零。这样，在弱磁场中，在低加速时，人们总可以使两个周期相配合。

图3.13　在磁场中，一对带相反磁荷的黑洞相互加速飞离

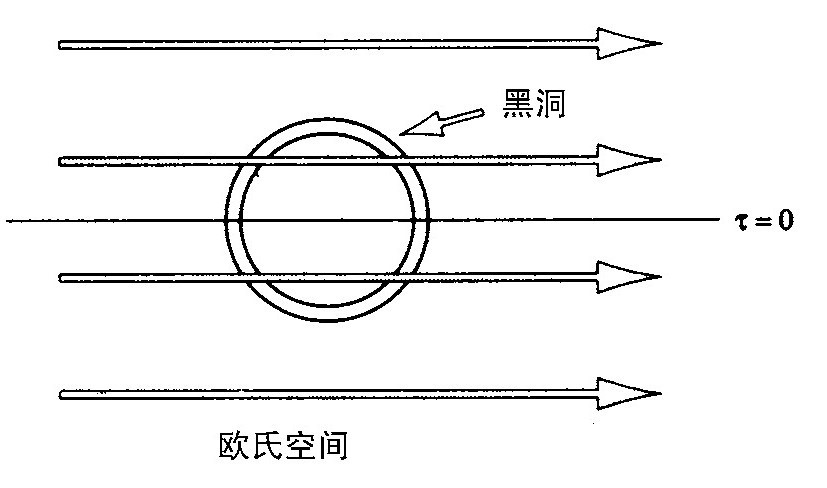
图3.14　在欧氏空间中一个带荷的黑洞沿着圆周运动

正如在电子对产生的情形，人们可以利用欧氏解的虚时间的下半部和洛氏解的实时间的上半部相连接来描述黑洞对的产生（图3.15）。人们可以认为黑洞在欧氏区域隧道穿透，并作为一对带反号磁荷的黑洞出现，它们被磁场加速而相互飞离。由于加速黑洞解在无穷趋于均匀的磁场，所以不是渐近平坦的。但是人们仍然可以用它来估计在磁场的局部区域黑洞对的产生率。

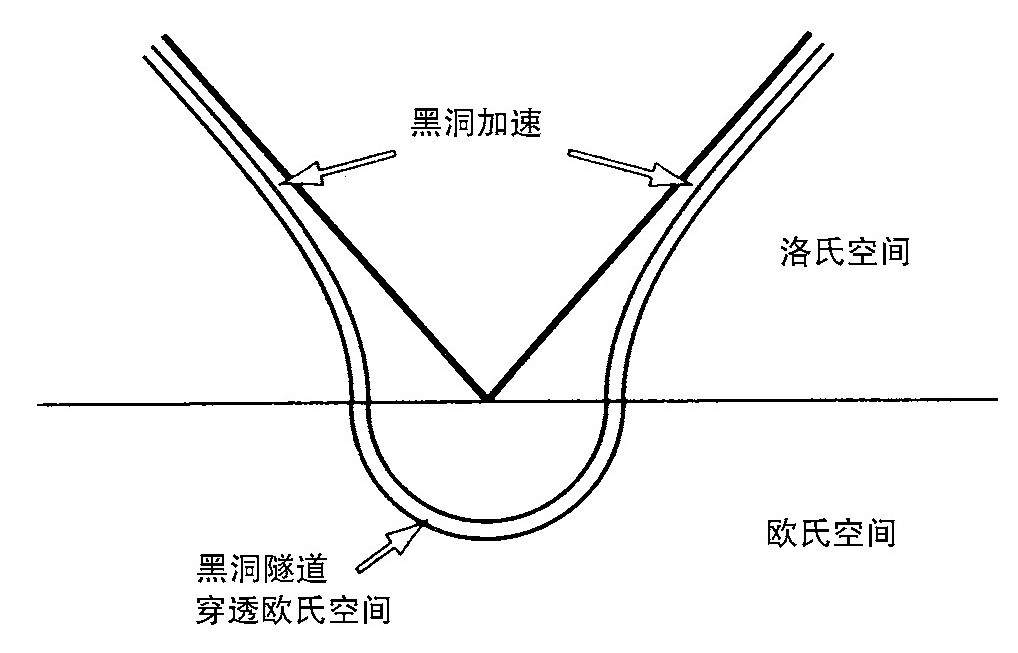
图3.15　还可以利用半张欧氏图和半张洛氏图的连接来描述一对黑洞的隧道穿透的产生

人们可以想象，黑洞在创生之后相互远离并进入无磁场的区域。然后可以把每个黑洞当作处于渐近平坦空间之中而分别处理。人们可以把任意大量的物质和信息抛入每个黑洞。这些黑洞辐射并丧失质量。然而，由于不存在带磁荷的粒子，所以它们不会失去磁荷。这样，它们最终就回到其原先的状态，质量比磁荷稍大一些而已。然后人们可以把这两个黑洞弄到一起使之相互湮灭。其湮灭过程可认为是对产生的时间反演。这样，这可由欧氏解的上半部和洛氏解的下半部相连接来描述。在对产生和对湮灭之间的一段很长的洛氏阶段中，黑洞相互离开，吸积物质，然后再返回到一块。但是引力场的拓扑是欧氏恩斯特解的拓扑。这就是S²×S²减去一点（图3.16）。

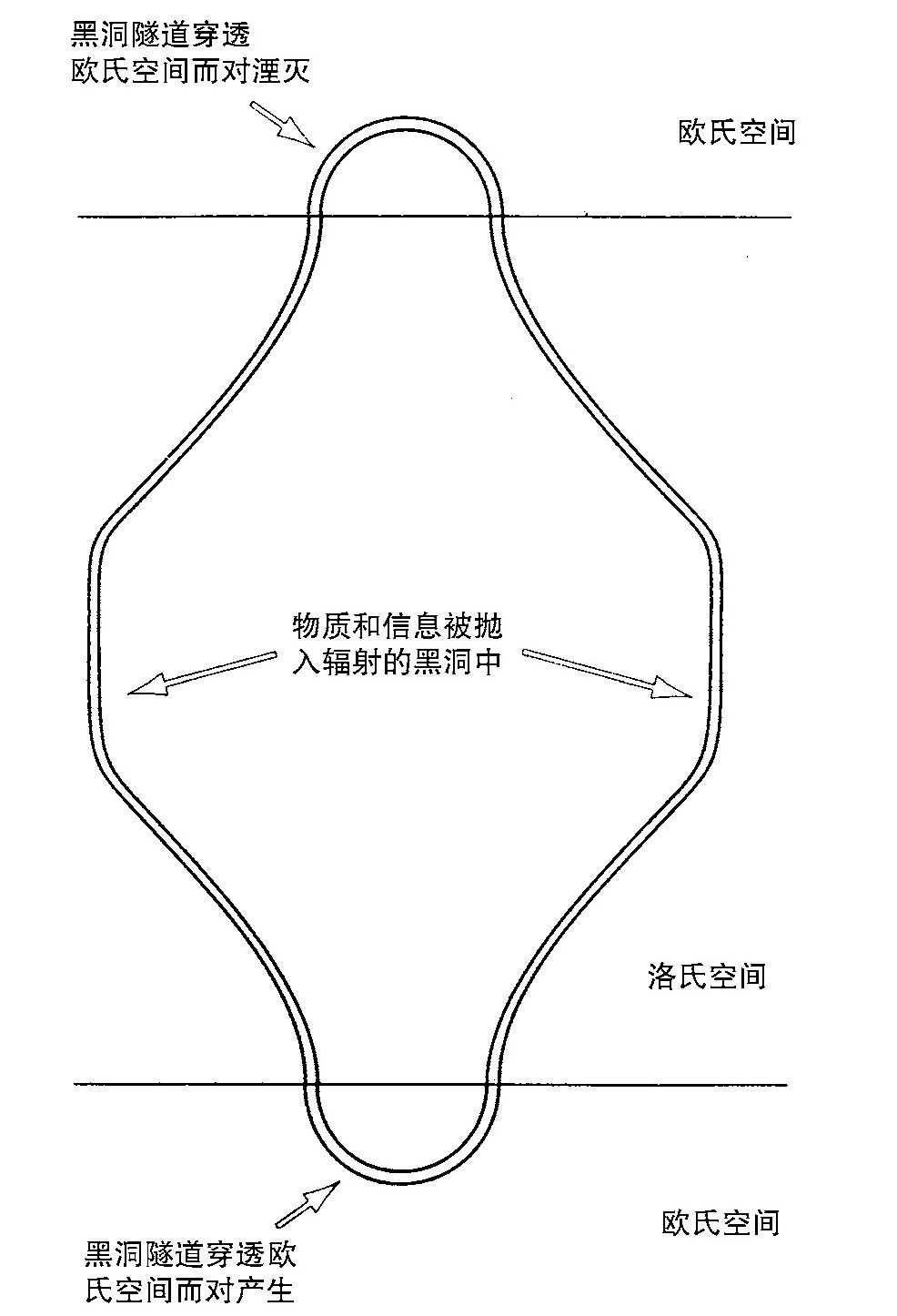
图3.16　黑洞对由于隧道效应产生而且最终又由于隧道效应湮灭

人们也许会担忧，由于在黑洞湮灭时其视界面积会消失，从而推广的热力学第二定律会被违反。然而，人们发现在恩斯特解中的加速视界的面积比没有对产生时所具有的面积更小。由于在两种情形下加速视界的面积都是无限大，因此这是一项相当精微的计算。尽管如此，在相当确定的意义上说，其面积差是有限的，并且等于黑洞视界面积加上有对产生以及没有对产生的解的作用量之差。这可以这么理解，对产生是零能过程，具有对产生的哈氏量和不具有对产生的哈氏量相同。我非常感谢赛蒙·罗斯和盖瑞·霍罗维茨为这次讲演及时地计算出这一减小量。这真是一桩奇迹——我是指结果，而不是他们得到的过程——它使我信服，黑洞热力学决非低能下的近似。我相信，即使我们必须进入量子引力的更基本理论，引力熵也绝不会消失。

人们从这一理想实验看到，当时空的拓扑和平坦闵可夫斯基空间的不同时，就会得到内禀引力熵以及信息丧失。如果对产生的黑洞比普朗克尺度大，则视界外的每一处的曲率都比普朗克尺度小。这表明我忽视三阶或更高阶的微扰项所引起的近似应是可靠的。这样，在黑洞中信息会丧失的结论应是可信的。

如果在宏观黑洞中信息丧失，那么它也应在因度规量子起伏出现的微观的虚黑洞过程中丧失。人们可以想象粒子和信息会落入这些黑洞并丧失掉。也许这里正是奥秘之所在。像能量和电荷这样的和规范场相耦合的量是守恒的，但是其他信息以及全局的荷会被丧失。这对于量子理论而言具有深远的含义。

人们通常假定，一个处于纯粹量子态的系统，以一种幺正的方式通过一系列纯粹量子态而演化。但是，如果通过黑洞的出现和消失而引起信息丧失，则不存在幺正演化。相反地，信息丧失意味着，在黑洞消失之后，终态就变成所谓的混合量子态。这可被认为是不同纯粹量子态的一个系综，每一纯态各具有自己的概率。但是，因为任何一种状态都不确定，不能利用和任何量子态干涉的办法把这种终态的概率减小到零。这表明引力在物理中引进了一种新水平的不确定性，这种不确定性超越于通常和量子理论相关的不确定之上。我将在下一次讲演（第5章）中指出，我们或许已经观测到这种额外的不确定性。这表示科学决定性论的终结，我们不能确定地预言未来。看来上帝在它的袖子里仍有一些令人无法捉摸的诡计。

图3.17