附录　注释

[A.1]R.Penrose, W.Rindler（1984），Spinorsandspace-time, Vol.I：Two-spinor calculus and relativistic felds，Cambridge University Press.R.Penrose, W.Rindler（1986），Spinorsandspace-time, Vol.II：Spinor and twistor methods in spacetime geometry，Cambridge University Press.

[A.2]P.A.M.Dirac（1982），Theprinciplesofquantummechanics，4th edn.Clarendon Press[1st edn 1930].E.M.Corson（1953）Introduction to tensors, spinors, and relatavistic wave equations.Blackie and Sons Ltd.

[A.3]C.G.Callan, S.Coleman, R.Jackiw（1970），Ann.Phys.（NY）5942.E.T.Newman, R.Penrose（1968），Proc.Roy.Soc.，Ser.A 305174.

[A.4]这是在广义相对论线性极限下的旋量-2 Dirac-Fierz方程。P.A.M.Dirac（1982），Theprinciplesofquantummechanics，4th edn.Clarendon Press[1st edn 1930].M.Fierz, W.Pauli（1939），‘On relativistic wave equations for particles of arbitrary spin in an electromagnetic field’，Proc.Roy.Soc.Lond.A173211—232.

[B.1]现在的形式很可能需要修正，从而把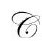中衰减的静止质量也包含进来（遵从§3.2）。然而，这很可能使问题大为复杂，所以到目前为止我只限于关心更容易处理的情形，假定我们的“颈圈”不包含中的静止质量。

[B.2]我并不认为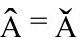本身是一个大不了的假设，那不过是一个习惯问题。眼下看来，物理常数从一个世代到下一个世代的改变，由其他物理量来替代，不过是一个常数的安排问题。进一步说，我们注意，§3.2中引入的标准“普朗克单位”的替换，可以认为是用Λ=3来代替G=1的条件，因为这更符合我们这儿的CCC形式。

[B.3]E.Calabi（1954），“The space of Kihler metrics”，Proc.Internat.Congress Math.Amsterdam, pp.206—207.

[B.4]幽灵场（Phantom field）：很多文献都用这个词，意思不尽相同。

[B.5]见注释3.9。

[B.6]见注释3.9。

[B.7]The full freedom is given by the replacement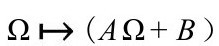/（BΩ+A），with A and B constant, whereby.But this ambiguity is dealt with by the demand thatΩhave a pole（andωa zero）at X.

[B.8]K.P.Tod（2003），‘Isotropic cosmological singularities：other matter models'，Class.Quant.Grav.20521—534.[DOI：10.1088/

[B.9]0264—9381/20/3/309]

[B.10]见注释3.28。

实际上，这个算子显然是C.R.Le Brun（1985）在他用扭量理论来定义“爱因斯坦丛”时引进的“Ambi-twistors and Einstein’s equations”，Classical Quantum Gravity2555—563），它构成了East-wood和Rice引进的更一般的一族算子的一部分[M.G.Eastwood and J.W.Rice（1987），“Conformally invariant differential operators on Minkowski space and their curved analogues”，Commun.Math.Phys.109207—228，Erratum，Commun.Math.Phys.144：（1992）213]。它与其他场合也有关系[M.G.Eastwood（2001），“The Einstein bundle of a nonlinear graviton”，inFurther advances in twistor theory vol III，Chapman&Hall/CRC, pp.36—39.T.N.Bailey, M.G.Eastwood, A.R.Gover（1994），“Thomas’s structure bundle for conformal, projective, and related structures”，Rocky Mtn.Jour.Math.24：1191—1217.]现在它成为所谓“与爱因斯坦共形的”算子，也参见下书p.124的脚注：R.Penrose, W.Rindler（1986），Spinors and spacetime, Vol.II：Spinor and twistor methods in spacetime geometry，Cambridge University Press.

[B.11]这个解释是K.P.Tod向我指出的。见PR1986，那个条件被称为“渐进爱因斯坦条件”。R.Penrose, W.Rindler（1986），Spinors and spacetime, Vol.II：Spinor and twistor methods in spacetime geometry，Cambridge University Press.

[B.12]还可以从其他方式来看引力常数的这个有效符号改变，其中一个是比较通过共形无限远时辐射场的“Grgin行为”和引力源的“反Grgin行为”；见Penrose and Rindler（1986），§9.4，pp.329—332.R.Penrose, W.Rindler（1986），Spinorsandspace-time, Vol.II：Spinor and twistor methods in spacetime geometry，Cambridge University Press.

[B.13]K.P.Tod，私人通信。