第2章 奇异的大爆炸
2.1 我们膨胀的宇宙
大爆炸:我们相信到底发生了什么?有明确的观测证据证明原初爆炸真的发生过——从而我们整个宇宙才从它诞生出来?前面部分提到的问题,其核心在于:如此暴烈的事件,怎么能代表熵值极其微小的状态呢?
起初,我们对宇宙起源于爆炸的信心,来自美国天文学家哈勃(Edwin Hubble)令人信服的宇宙正在膨胀的观测。那是在1929年,尽管斯里弗(Vesto Slipher)早在1917年就发现了膨胀的信号。哈勃的观测则相当令人信服地证明遥远星系正在远离我们而去,退行的速度大约正比于它们到我们的距离。所以,如果我们倒推回去,就会得出万物迟早会在某个时候聚拢在一起的结论。万物的汇聚将产生巨大的爆炸——即我们今天说的“大爆炸”——所有物质归根结蒂都从它起源而来。后来的很多观测和具体的实验(有些我马上就说)都证实而且强化了哈勃最初的结论。
哈勃的思路基于遥远星系发出的光谱线的红移。名词“红移”指的是遥远星系的不同原子发射的频谱在地球上看来会略向红端移动(图2.1),这是一种均匀的频率减小,可以解释为多普勒频移,[2.1]即因为观测对象以可观的速度离开观测者而产生的谱线红化现象。距离我们越远的星系红移越大,红移与视距离的关系正好符合哈勃的宇宙在空间均匀膨胀的图像。
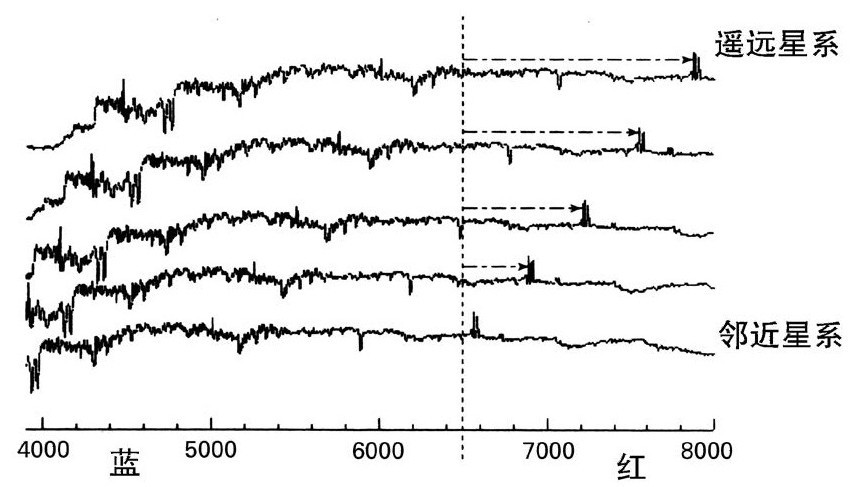
图2.1 遥远星系的原子发出的谱线的“红移”与多普勒频移的解释一致
接下来的年月里,观测和解释都更加精密。可以说,不仅哈勃原来的观点被普遍证实了,最近的工作更是非常具体地说明了宇宙膨胀速率如何随时间而变化,呈现了一幅我们今天普遍接受的图景(尽管在一些细节问题上还能听到反对的声音[2.2])。特别是,关于宇宙物质都聚集在起点的那个时刻——也就是我们所说的“大爆炸”,[2.3]我们已经确立了一个相当严格且大家都认同的年代:大约1.37×1010年前。
我们不能认为大爆炸局限于空间的某个特殊区域。根据爱因斯坦的广义相对论,宇宙学家们的观点是,大爆炸在发生的时刻包含了宇宙的整个空间范围,因而囊括了物理空间的全部,而不仅是其中的物质组成。因此,在一定意义上,那个时刻的空间应该是非常微小的。为理解这类疑难,有必要熟悉爱因斯坦的弯曲时空的广义相对论思想是怎么回事。在2.2节,我将以非常严格的方式讲述爱因斯坦的理论,不过现在我们只讲一个人们经常用的类比,即正在吹胀的气球。宇宙犹如气球的表面随时间而膨胀,而整个空间也随之膨胀,并不存在一个开始膨胀的宇宙中心点。当然,气球膨胀所在的3维空间确实包含气球内的一点作为气球表面的中心点,但这一点本身不是气球表面的一部分,我们只是用那个表面来代表整个宇宙的空间几何。
观测所揭示的依赖于时间的宇宙膨胀确实令人惊奇地满足爱因斯坦广义相对论的方程,不过条件是那理论似乎还必须包含两个意外的因子,即现在通常说的“暗物质”和“暗能量”(两个有点儿不幸的名字)[2.4]。两个因子对我要读者随时参考的方案都有着非常重要的意义(见3.1和3.2节)。它们眼下是现代宇宙学标准图像的组成部分,但应该指出并不是本领域的所有专家都完全接受它们。[2.5]不过就我而言,我很乐于接受存在某种不可见材料——“暗物质”——它有着我们未知的性质,还占宇宙物质的70%,而且也认同爱因斯坦的广义相对论方程必须具有他本人在1917年提出的修正形式(尽管他后来否决了),在方程里包含一个正而小的宇宙学常数Λ(“暗物质”的最可能形式)。
应该指出,爱因斯坦的广义相对论(有或没有小常数Λ)在太阳系尺度经受了极好的检验。即使非常实用的全球定位系统(如今正普遍应用),其运行精度也依赖于广义相对论。更令人难忘的是爱因斯坦理论模拟脉冲双星系统的异乎寻常的精度——总体精度达到了1014分之一(为确定双星系统PSR-1913+16发出的脉冲信号的时间间隔,在大约40年的周期里,精度达到了大约每年10-6秒)。[2.6]
最初的宇宙学模型,基于爱因斯坦理论的,是俄罗斯数学家弗里德曼(Alexander Friedmann)在1922年和1924年提出的。在图2.2中我勾勒了这些模型的时空历史,描绘了3个时间演化情形(令Λ=0),其中宇宙的空间曲率分别是正、零和负。[2.7]照我一贯的约定,几乎所有时空图中,竖直方向代表时间演化,水平方向代表空间。在这3种情形,都假定空间几何是完全均衡的(即均匀和各向同性的)。具有这种对称性的宇宙学模型叫弗里德曼—勒梅特—罗伯森—沃克模型(Friedmann—Lemaitre-Robertson-Walker, FLRW)。最初的弗里德曼模型是它的特例,其物质表述为一种无压力流体,即“尘埃”(也见2.4节)。
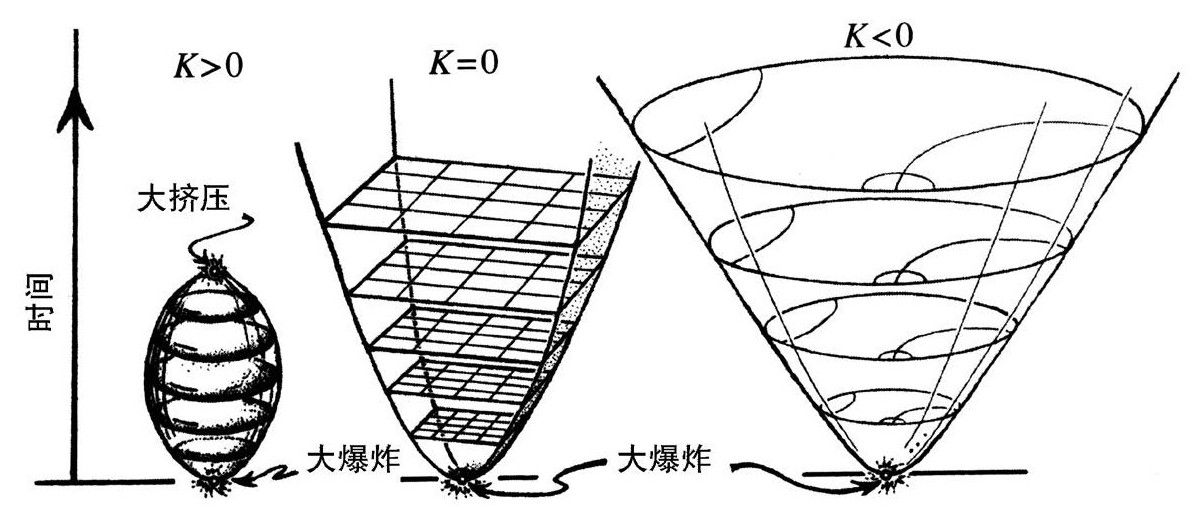
图2.2 弗里德曼宇宙模型的时空历史,空间曲率分别为正、零和负(从左到右)
根本来说,[2.8]我们要考虑的空间几何只有3种情形:K>0的正空间曲率情形,空间几何是球面(如我们在前面说过的气球)的3维类比;K=0的平直情形,空间几何是我们熟悉的3维欧几里得几何;负曲率K<0的双曲3维空间几何。幸运的是,德国艺术家埃舍尔(Maurits C.Escher)用镶嵌的天使和魔鬼精妙地描绘了这些不同类型的几何(图2.3)。我们必须记住,这些图描绘的是2维空间几何,但所有3种几何的3维类比也存在于全部的3个空间维。

图2.3 埃舍尔描绘的三种基本的均匀平面几何:(a)椭圆型(正曲率,K>0);(b)欧几里得几何(平直,K=0);(c)双曲型(负曲率,K<0)Maurits C.Escher公司版权所有(2004)
这些模型都从一个“大爆炸”的奇异状态开始——“奇异”指物质密度和时空几何的曲率在那个初始状态变得无穷大——从而爱因斯坦的方程(以及我们所知的整个物理)在那个奇点“崩溃”了(不过,见3.2节和附录)。要注意的是,这些模型的时间行为都相当程度地反映了其空间行为。空间有限的情形[K>0,图2.3(a)]也是时间有限的情形,不仅有一个初始的大爆炸奇点,还有一个终点,即普遍所指的“大挤压”。另外两种情形[K≤0,图2.3(b),(c)]不仅是空间无限的,也是时间无限的,膨胀会无限进行下去。[2.9]
然而,大约自1998年两个观测小组——分别由佩尔穆特(Saul Perlmutter)和施密特(Brian P.Schmidt)领导——分析他们的遥远超新星爆发的数据以来,[2.10]越来越多的证据强烈表明宇宙的膨胀在后期阶段并不符合图2.2所示的标准弗里德曼宇宙学预言的演化速率。相反,我们的宇宙看起来已经开始加速膨胀了,其速度似乎只有用包含了宇宙学常数Λ(具有正的微小数值)的爱因斯坦方程才能解释。这些连同后来的各种观测提供了相当可信的证据,[2.11]说明Λ>0的弗里德曼宇宙模型具有指数式膨胀的特征。这种指数式膨胀不仅发生在K≤0的情形——在这种情形,即使到遥远的未来Λ=0时也总会无限膨胀——也发生在空间闭合的K>0的情形,只要Λ足够大,能克服闭合弗里德曼模型具有的空间重新坍缩的倾向。实际上,确有证据真的表明存在一个足够大的Λ——因而K的数值(和符号)对膨胀速率就显得不那么重要了——而确实出现在爱因斯坦方程的Λ的(正)值,将在演化的后期起主导作用,激发指数式的膨胀,在可接受的观测范围内独立于K的数值。于是,我们有一个膨胀速率基本符合图2.4的曲线的宇宙,其时空图的表现符合图2.5。
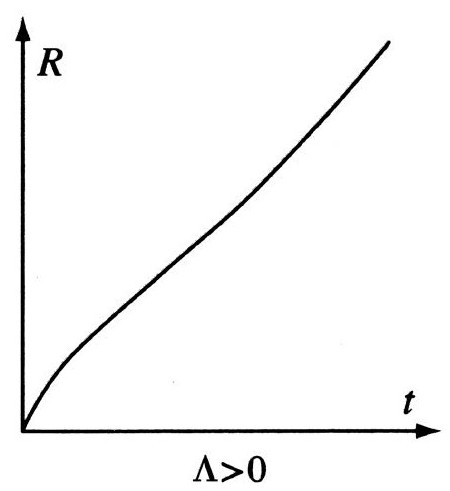
图2.4 正Λ情形的宇宙膨胀速率,最终以指数形式增长
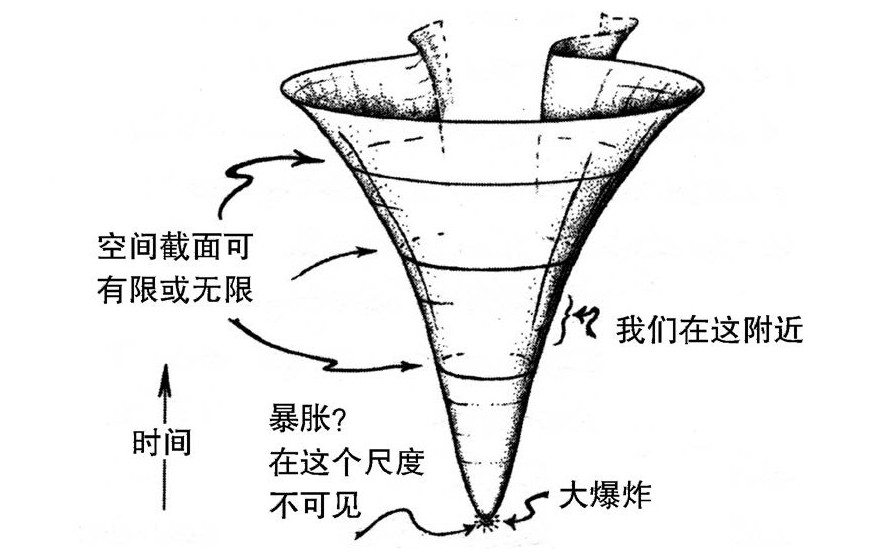
图2.5 宇宙的时空膨胀,正Λ情形的图像(示意图,不受K值的影响)
这样看来,我不必特别关心宇宙空间几何的那3种可能性之间的区别。实际上,当前的观测表明宇宙的整体几何非常接近K=0的平直情形。一方面说,这多少有些不幸,因为它意味着我们真不知道宇宙的空间几何到底像什么样子——例如,宇宙一定是空间闭合的抑或是空间无限的——如果缺乏有力的理论根据相信平直时空,那么总曲率是正是负,都有一定的可能性。
另一方面,很多宇宙学家认为宇宙暴胀的观点就提供了一个有力的理论根据,令我们相信宇宙的空间几何一定真的是平直的(K=0,除了相对小的局部偏离),所以他们为接近平直的观测结果感到欣喜。宇宙暴胀是一个理论建议,认为在大爆炸之后的一个非常小的时间间隔内(大约在10-36到10-32秒之间),宇宙经过了一个指数式膨胀,线性尺度增大了约1030或1060(甚至10100)倍。我以后还要细说宇宙暴胀(见2.6节),不过现在我只是提醒读者我对那个特别的建议没多大兴趣,尽管它在当下宇宙学家中赢得了普遍的欢迎。不管怎么说,宇宙历史的早期出现那么一个暴胀的阶段,不会改变图2.2和图2.5的面貌,因为暴胀的效应只显现在紧跟大爆炸的极早时期,不会出现在图2.2和图2.5所画的尺度。另外,我将在本书提出的一些观点,大概能可信地替代暴胀来解释那些观测现象——它们似乎只是在当前流行的宇宙学纲领下才依赖于暴胀(见3.5节)。
除了这些考虑,我呈现2.3(c)的图画还有一个很不一样的动机,因为它说明了一点对我们以后有着根本意义的东西。埃舍尔的这幅美妙版画是基于双曲面的一种特殊表示,那是天才的意大利几何学家贝尔特拉米(Eugenio Beltrami)在1868年提出的几种表示之一。[2.12]大约14年后,同样的表示被法国大数学家庞加勒(Henri Poincaré)重新发现了,所以它们通常是与他的名字联系在一起的。为避免名词的混淆,我通常会简单地称它为双曲面的共形表示,名词“共形”指的是那个几何中的角度在画它的欧几里得平面中都得到了正确的表示。共形几何的思想将在2.3节做更详细的解说。
我们将认为,这个几何中所有魔鬼在所示的双曲几何中都是全同的;同样,所有的天使也是全同的。显然,根据背景的欧几里得度量,我们越靠近圆周的边界,它们的尺寸越小;但角度或无穷小形状的表示在接近边界时也是真实的。圆边界本身代表几何的无穷大,我要在这里向读者指出的,正是这种表现为有限光滑边界的无穷大共形表示,它将在我们以后的思想中起着核心作用(特别是2.5节和3.2节)。
2.2 无所不在的微波背景
20世纪50年代,一个流行的宇宙理论是所谓的稳恒态模型,是戈尔德(Thomas Gold)和邦迪(Hermann Bondi)在1948年提出的[2.13],那时他们都在剑桥大学。理论要求物质在整个空间以极低的速率连续生成。物质以氢分子形式出现——每个分子包含一个质子和一个中子,从真空生成——产生的速率极其微小,大约每十亿年每立方米生成1个原子。这个速率恰好能填补因为宇宙膨胀引起的密度减小。
从许多方面看,这是一个很有哲学趣味和美学愉悦的模型,因为它的宇宙不需要时间和空间的起源,很多性质都可以归结到它的自我繁殖。这个理论提出没多久,我就在1952年进剑桥大学读研究生(研究纯数学,但对物理学和宇宙学有浓厚兴趣[2.14])。后来,1956年,我又作为研究者回到剑桥。在剑桥时,我认识了稳恒态理论的3个创立者,当然也发现这个模型很有趣,论证也很诱人。然而,等我快离开剑桥时,赖尔(Martin Ryle)爵士(也在剑桥)在玛拉德(Mullard)射电天文台进行的星系距离计算,开始呈现出清楚的反对稳恒态模型[2.15]的证据。
但真正索它命的是美国人彭齐亚斯(Arno Penzias)和威尔逊(Robert W.Wilson)在1964年偶然发现的微波电磁辐射,它来自空间的所有方向。其实,在20世纪40年代后期,盖莫夫(George Gamow)和迪克(Robert Dicke)就根据当时更传统的“大爆炸”理论预言了那种辐射,那种今天能看到的辐射有时被描述为“大爆炸的闪电”,辐射从宇宙发射以来随巨大膨胀引起的巨大红移而从4000K冷却到比绝对零度高几度[2.16]。彭齐亚斯和威尔逊确认了他们看到的辐射(大约2.725K)是真实的,而且一定来自太空深处,然后就去问迪克。迪克很快指出他们那个令人迷惑的观测可以解释为盖莫夫以前预言的结果。那个辐射有过五花八门的名字(如“辐射遗迹”、3度背景等),今天都通称为CMB,代表“宇宙微波背景辐射”[2.17]。1978年,彭齐亚斯和威尔逊因为这一发现获得诺贝尔物理学奖。
然而,构成我们今天“看到”的CMB的光子来源并不真的是那个“实际的大爆炸”,因为那些光子直接来自所谓的“最后的散射曲面”,它出现在大爆炸379000年之后(即宇宙年龄是现在的1/36000)。更早的时候,宇宙对电磁辐射是不透明的,因为它充满了大量分离的相互围绕旋转的带电粒子——主要是质子和电子,构成我们说的“等离子体”。光子在这些物质中会多次散射,被大量吸收和生成,宇宙则远离透明状态。这种“云雾”状态将持续到所谓的“解耦”时期(即“最后的散射”出现时),那时候宇宙变得透明,因为分离的电子和质子都足够冷却,可以配成粒子对,以氢原子的形式出现(也生成少数其他原子,主要是23%的氦,其核——叫α粒子——是宇宙形成最初几分钟的产物之一)。然后,光子从那些中性原子脱离出来,几乎毫无阻碍地旅行,成为我们今天认识的CMB的辐射。
自20世纪60年代的最初观测以来,人们通过大量实验获得了越来越好的关于CMB的性质和分布的数据,如今有了非常详尽的信息,完全改变了宇宙学学科的面貌——它过去是猜想多而数据少,现在则成了一门精确科学,尽管仍有猜想,但也有大量数据来规整猜想!一个特别值得注意的实验是国家航空航天局(NASA)在1989年发射的COBE(宇宙背景探测者)卫星,它惊人的观测为斯穆特(George Smoot)和马瑟(John Mather)赢得了2006年诺贝尔物理学奖。
CMB有两个非常突出而重要的特征,在COBE看来尤为显著,我想专门说几句。第一个特征是,观测的频谱异乎寻常地接近普朗克(Max Plank)在1900年为解释所谓“黑体辐射”的性质而提出的曲线(那标志着量子力学的起点)。第二个特征是,CMB在整个天区极其均匀。每个特征都向我们透露了一些关于CMB性质的非常基本的东西,还有它与第二定律的奇妙关系。现代宇宙学的许多东西都从这儿开始进步,也更加关注在CMB中看到的对均匀性的微妙偏离。我以后会讨论其中的一些问题(见3.6节),不过现在我只需要指出这两个更吸引眼球的事实,我们马上会看到,它们对我们有着极其重大的意义。
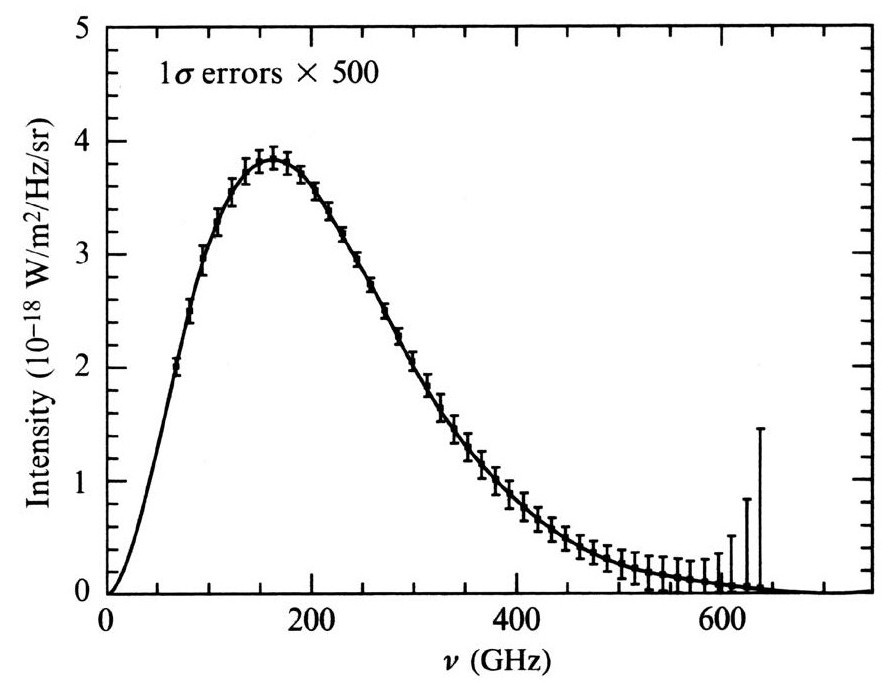
图2.6 COBE初始观测的CMB频谱,补充了后来更精确的观测数据。注意“误差棒”放大了500倍。本图表明观测数据精确符合普朗克频谱
图2.6描绘了CMB的频谱,它基本根据COBE的最初观测,而我们现在已经从后来的观测获得了更高的精度。竖轴度量辐射的强度,是不同频率的函数,频率表示在水平轴上,向右增大。连续曲线是普朗克的“黑体曲线”,[2.18]由具体的公式给出,代表量子力学所说的热平衡在任意特定温度T的辐射谱。短竖线代表误差区间,大致告诉我们观测强度所在的范围。不过应该指出,这些误差区间大约放大了500倍,所以实际的观测点比这儿显示的更接近普朗克的曲线——实际上,在肉眼看来,即使在最右边误差最大的区域,观测点也几乎落在墨水曲线的线条里面!其实,CMB所呈现的观测强度与普朗克黑体曲线之间的一致,在已有的观测科学里是最精确的。
这说明了什么?它似乎告诉我们,我们看到的东西来自一个肯定是热平衡的状态。但“热平衡”又意味着什么呢?请读者回头看图1.8,我们在那儿看到“热平衡”这个词儿标记的是相空间中(迄今)最大的粗粒化区域。换句话说,这是代表最大熵的区域。但我们再回想一下1.6节插入的论证。那些论证告诉我们,第二定律的整个基础必须用下面的事实来解释:宇宙的初始状态——我们当然指的是大爆炸——必须是一个熵异常小的(宏观)状态。我们看到的似乎正好相反,是一个最大熵的(宏观)状态!

图2.7 宇宙的绝热膨胀,描述为一系列等体积的最大粗粒化区域
这儿有一点必须说明,那就是宇宙在膨胀,从而我们看到的不可能真的是“平衡”态。然而,实际发生的是一种绝热膨胀,这儿的“绝热”大致指熵保持为常数的“可逆”变化。这种“热状态”其实保留在早期的宇宙膨胀中,这个事实是托尔曼(R.C.Tolman)[2.19]在1934年指出的。在3.3节我们会看到更多的托尔曼对宇宙学的贡献。从相空间看,这个图更像图2.7而不是图1.8,膨胀表现为一系列体积大致相等的最大粗粒化区域。在这个意义上,膨胀仍然可以看作一种热平衡。
那么我们似乎还是看见最大的熵。这个论证肯定有严重的问题。并不是说宇宙观测令人惊讶,根本不是那么回事。从某种意义说,观测接近我们的预期。既然真的发生过大爆炸,而初始状态又必须符合广义相对论宇宙学提出的标准图景,那么一个炽热而均匀的初始状态正是预料之中的。那么症结在哪儿呢?也许你会惊讶,问题的症结就在于假定宇宙应该符合广义相对论宇宙学的标准图景!我们需要仔细考察这个假定,看问题出在哪儿。
首先,我们回想一下爱因斯坦的广义相对论都说了什么。毕竟,它用时空的曲率来描述引力场,是一个异常精确的引力理论。我会随时补充这个理论的东西,不过现在我们先用更老的牛顿引力理论来思考——它当然也是非常精确的——然后以更一般的方式去认识它与第二定律的关系——当然是热力学的第二定律,而不是牛顿的第二定律!
通常,考虑第二定律时,都用密封在盒子里的气体来讨论。沿着这样的思路,我们设想盒子的一角有一个小格子,气体最初就封闭在那个小格子里。小格子的门开启时,气体便自由流入盒子,我们预期它会很快在盒子里均匀扩散,熵在这个过程中遵从第二定律而不断增大。于是,气体均匀分布的宏观状态的熵远远大于气体限制在小格子的熵,见图2.8(a)。不过,现在我们考虑一个看起来类似的情形,但假想盒子像星系那么大,而且用一颗颗在盒子里运行的星体来代替一个个气体分子。这种情形与气体情形的差别并不仅仅在于物质的尺度,我还要让尺度与我们的讨论无关。真正相关的事实在于,星体会通过不息的引力相互吸引。我们可以设想星体的分布最初在星系大的盒子里是相当均匀的。但随着时间的流逝,我们发现星体有聚集成团的趋势(而且聚集的速度通常会很快)。这样,均匀的分布并不是熵最高的,星体不断地聚集会产生不断增大的熵。见图2.8(b)。
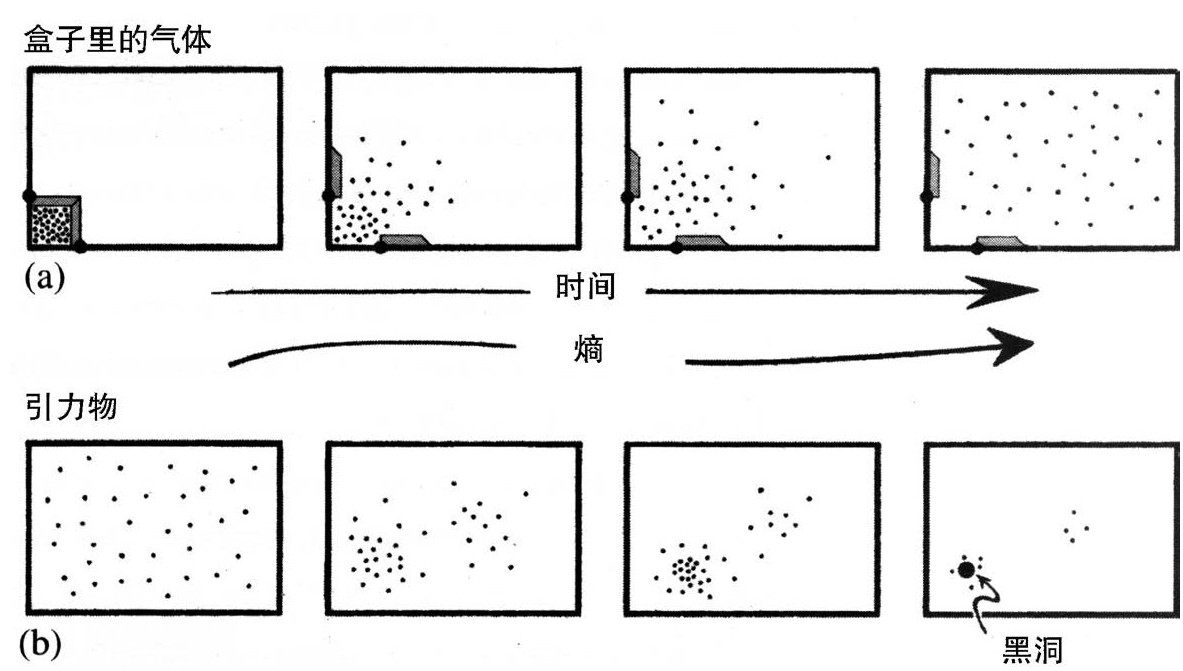
图2.8(a)气体起初被约束在盒子的一个角落的格子里,释放之后它会均匀分布在整个盒子里;(b)在星系尺度的盒子里,星体起初均匀分布,但在整个时间过程里不断聚集成团:这种情形下,均匀分布不是最高熵的状态
我们可以问,现在与那个熵达到极大的热平衡相应的状态是什么?这个问题不可能在牛顿理论的框架下得到正确回答。如果考虑由遵从牛顿平方反比律相互吸引的大质量点粒子组成的系统,那么我们可以想象这样的状态:有些粒子会越靠越近,运动越来越快,以至无限快地运动,无限靠近地聚集,那假想的“热平衡”状态根本不可能存在。在爱因斯坦的理论中,这种情形会令人满意得多,因为当物质凝聚成黑洞时,那种“聚集”就达到了饱和。
我们将在2.4节细说黑洞,在那儿我们将知道黑洞的形成代表熵的巨大增加。实际上,在宇宙演化的现阶段,最大的熵都来自巨大的黑洞,如我们银河系中心的黑洞,质量大约是太阳的4000000倍。这些天体的总熵完全超出了CMB的熵——以前认为它代表了宇宙熵的主要来源。因此,从CMB生成以来,熵通过引力凝聚而大大增加了。
这关系到前面说的CMB的第二个特征,即它的温度在整个天空几乎是均匀的。多均匀呢?微小的温度偏差可以理解为多普勒频移,源于地球相对于整个宇宙的物质分布并不是完全静止的。地球的运动有不同的来源,如它绕着太阳转,而太阳绕着银河系转,银河系还因为其他相对邻近的物质分布的引力作用而运动。所有这些运动组合起来形成地球的“本动”。结果,在我们运动方向的天空,CMB的温度看起来略微提高了,[2.20]而在相反方向的天空,温度略微降低了,整个天空的温度变化模式也很容易从地球的运动计算出来。经过这样的修正,我们发现CMB的天空有着异乎寻常的均匀温度,只有大约十万分之几的偏离。
这个结果告诉我们,宇宙至少在最后散射曲面上是异常均匀的,如图2.8(a)右图和图2.8(b)左图。于是我们有理由假定,只要引力作用可以忽略,宇宙的物质(最后散射时)其实就处于它所能达到的高熵状态。引力影响之所以很小,是因为均匀性,但正是这种物质分布的均匀性为后来引力发生作用时的巨大熵增提供了潜在的可能。于是,只要我们考虑引力自由度的参与,大爆炸的熵图像就将彻底改变。总的说来,正因为我们假定宇宙接近空间均匀和各向同性——有时也叫“宇宙学原理”,[2.21]是FLRW宇宙学的基础,特别是2.1节讨论的弗里德曼模型的核心——引力自由度才会在初始状态被大大地压缩。早期的空间均匀代表着宇宙极低的初始熵。
一个自然的问题是:宇宙学的均匀性与我们熟悉的第二定律究竟有什么关系呢?它可是渗透到了我们世界的很多具体的物理行为。第二定律有大量普通的例子,似乎与引力自由度在早期宇宙被压缩的事实没有一点儿关系。但联系确实是有的,而且我们也不难从这些普通的第二定律的例子追溯到早期宇宙的均匀性。
例如,我们考虑1.1节的那个从桌子边缘滚下地板并打碎的鸡蛋(见图1.1)。从概率说,鸡蛋从桌子边缘滚下打碎的熵增过程是最可能发生的,只要我们假定那个完好的在桌子边缘的鸡蛋开始的时候处于低熵状态。第二定律的疑惑不在于熵随事件的增加,而在于事件本身,即鸡蛋怎么会碰巧找到最初的极低熵状态。第二定律告诉我们,当我们越来越远地追溯系统的过去,会发现系统以前必须通过一系列越来越不可能的状态,才能达到那个极不可能的状态。
大概有两件事情需要解释。一个是鸡蛋怎么会上桌子,另一个是鸡蛋本身的低熵结构从何而来。实际上,鸡蛋的原料精妙地形成对小鸡仔具有足够营养的完美包裹。但我们还是从更简单的问题开始,问鸡蛋是如何出现在桌子上的。可能的答案是,有人把它放在那儿,也许心不在焉。但人的干预只是可能的原因。显然一个活动的人体有很多高度组织的结构,那意味着低熵。他把蛋放在桌上只需要从相关系统——包括一个健康的人和他周围的有氧大气——的巨大低熵库里取出很少的一点儿。鸡蛋的情形与此有些相似,因为鸡蛋高度组织的结构,神奇地孕育着胚胎里的生命,也是地球上维持生命延续的宏大计划的一部分。地球生命的整体结构需要维持一种深层而微妙的结构,它无疑将熵保持在很低的水平。具体说来,存在一个无限复杂而又相互关联的结构,其演化遵从基本的生物学的自然选择原理,也服从许多具体的化学物质。

图2.9 从太阳到达地球表面的光子比从地球回到天空的光子具有更高的能量(更短的波长)。在总能量平衡的情况下(地球不会随时间越变越热),离开地球的光子必然多于达到地球的光子,就是说,到达的能量比离开的能量具有更低的熵
你可能问,那些生物和化学物质与早期宇宙的均匀性有什么关系呢?生物学的复杂不会让整个系统违背一般的物理学定律,如能量守恒定律;而且,它也不可能摆脱第二定律的约束。假如没有一个强大的低熵源——几乎所有地球生命赖以生存的源泉,也就是我们的太阳[2.22]——那么我们星球上的生命结构将轰然崩溃。可能有人认为太阳为地球提供了能源,但这并不完全正确,因为地球每天从太阳接收的能量大致等于地球返回黑暗天空的能量![2.23]假如不是这样,那么地球会被一直加热,直到那个平衡。生命所依赖的是太阳比黑暗的天空热得多,因而来自太阳的光子比从地球返回天空的红外光子有着高得多的频率(即黄光的频率)。于是,普朗克公式E=hν(见2.3节)告诉我们,来自太阳的单个光子所携带的能量平均说来远大于返回天空的单个光子所携带的能量。因此,携带相同能量离开地球的光子多于来自太阳的光子,见图2.9。光子越多意味着自由度越多,从而相空间体积越大。相应地,玻尔兹曼公式S=k lnV(见3.5节)告诉我们,来自太阳的能量所携带的熵远低于返回天空的能量的熵。
而在地球上,绿色植物通过光合作用实现了将来自太阳的相对高频率的光子转化为较低频率的光子,然后用获得的低熵,通过从空气中的CO2汲取碳放出O2来构筑它们的物质。动物吃了植物(或其他吃过植物的动物),也用这个低熵源和O2来维持它们自己的低熵状态。[2.24]当然,这同样适用于人和鸡,而且它还为我们构造那个完好的鸡蛋并将它放上桌子提供了低熵源!
所以,太阳对我们并不仅是提供能量,而且提供低熵形式的能量,这样才能(通过绿色植物)降低我们的熵,之所以如此,是因为太阳是黑暗天空里的一个热点。假如整个天空有着和太阳相同的温度,那么太阳的能量对地球的生命就没有任何意义。太阳在海洋掀起波浪涌向云天,也是同样的道理,也是依赖于温度的差异。
为什么太阳是黑暗天空里的一个热点呢?是啊,太阳内部发生着各种复杂过程,其中氢转化为氦的热核反应是重要的一部分。然而,问题的关键在于太阳是一个整体,它的出现是因为引力的作用将它凝聚在一起。如果没有热核反应,太阳仍然会发光,不过会因为收缩而变得更热,寿命会更短。在地球上,我们当然从热核反应得到很多,但如果不是因为引力的聚集先形成了太阳,它们也就没机会出现。于是,恒星从初始物质经过不停的引力聚集的熵增过程而形成(当然还要通过一定空间区域里的复杂过程)的潜力,是从均匀的引力主导的低熵状态开始的。
这一切最终源于我们面对一个有着非常特殊性质的大爆炸,它极端(相对)的低熵表现为它没有在初始时刻激活它的引力自由度。这是一种奇异的倾斜状态,为更好地理解它,我们将在下面3节深入爱因斯坦美妙的引力的弯曲时空图像。然后,在2.6和3.1节,我再回来讨论大爆炸所呈现的异常特殊的本性。
2.3 时空,零锥,度规,共形几何
1908年,当闵可夫斯基(Hermann Minkowski)——著名数学家,偶然成了爱因斯坦在苏黎世理工大学的老师——证明他能把狭义相对论的基本概念精炼成一种非同寻常的4维几何时,爱因斯坦对那种想法并没多大热情。可是后来他认识了闵可夫斯基的时空几何观的举足轻重的意义。实际上,他自己对闵氏思想的推广,构成了他的广义相对论弯曲时空基础的基本要素。
闵氏的4维空间包容了标准的3维空间和一个描述时间流的第4维。于是,这个4维空间的点通常代表一个事件,因为任何一个那样的点不但有空间的规定,也有时间的规定。就这个概念本身来说,真没什么太革命的东西。但闵氏思想——那可是真革命——的关键在于,他的4维空间几何并不自然分解为一个时间维和(更重要的)一系列对应于给定时刻的普通3维欧几里得空间。相反,闵氏时空有着不同的几何结构,奇妙地融合了欧几里得的古老几何思想。它实际上是时空的整体几何,将时空编织为一个不可分割的整体,完全概化了爱因斯坦狭义相对论的结构。
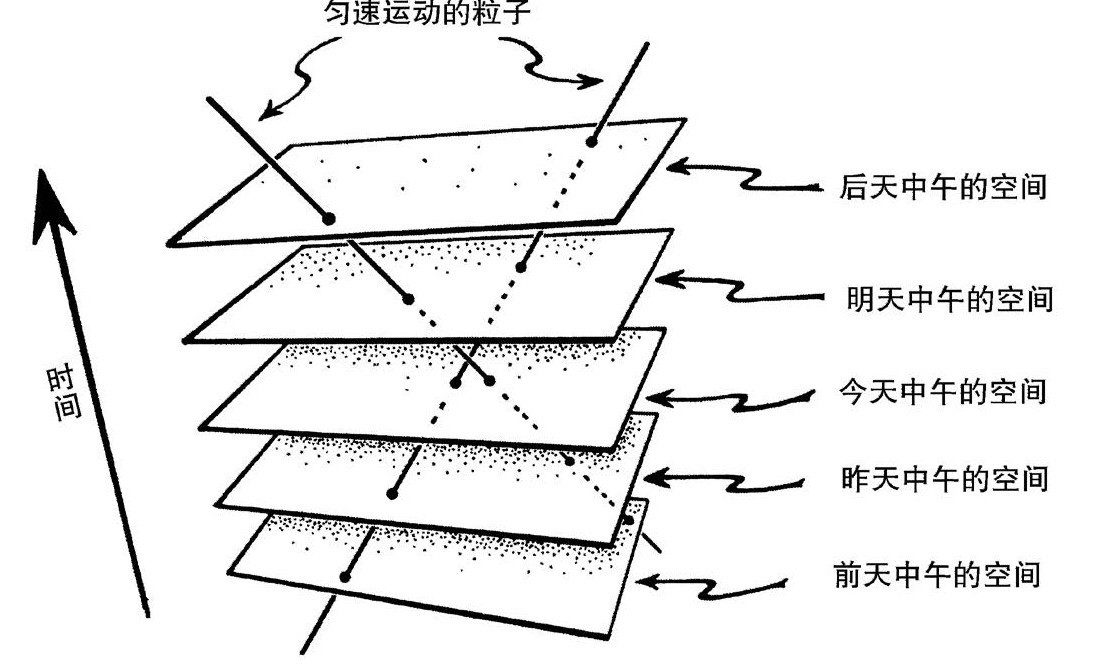
图2.10 闵可夫斯基之前的时空
于是,在闵氏的4维几何里,我们不再将时空看作一串3维曲面——每个面代表不同时刻的一个“空间”——的简单叠加(图2.10)。在那样的解释里,每个那样的3维曲面都描述了一组应该认为是同时发生的事件。在狭义相对论中,空间分离的事件的“同时”,没有绝对的意义。相反,“同时性”依赖于某个任意选择的观测者的速度。
当然,这是与我们的寻常经验冲突的,因为我们似乎真的发现相隔遥远的事件有一个独立于我们速度的同时性。但(根据爱因斯坦的狭义相对论)如果我们以堪比光速的速度运动,就会发现我们看来同时的事件对其他不同速度的观测者来说通常都不是同时的。而且,就非常遥远的事件来说,速度不需要很大。例如,两人在同一条路上沿相反方向散步,在他们走过对方的时刻,他们认为仙女座星系同时发生了若干事件,但那些事件其实可能相隔几个星期(见图2.11)![2.25]
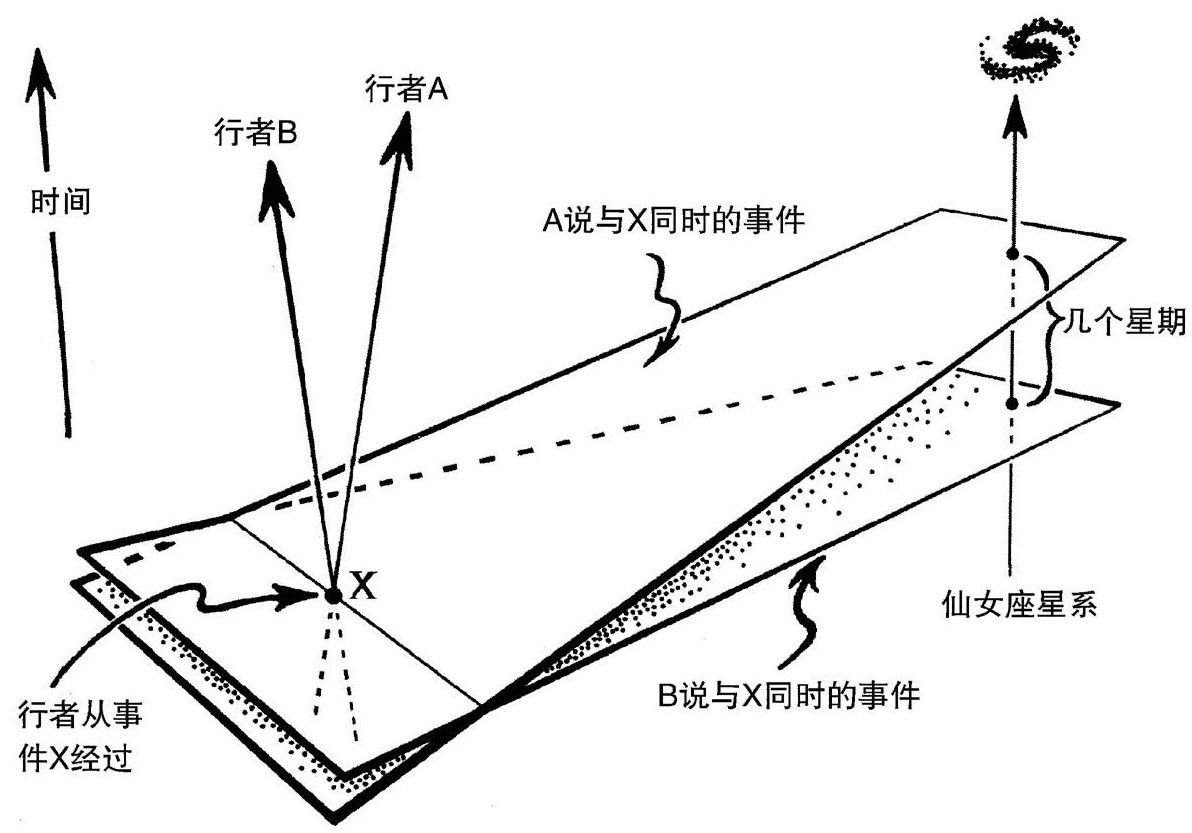
图2.11 两个漫步者从对方走过,在两人看来他们相互经过的事件X是同时的,而做出这个判断的依据却是仙女座星系中间隔几个星期的不同事件
根据相对论,“同时性”概念对遥远事件来说不是绝对的,而依赖于具体观测者的速度。所以,将时空分解为一系列同时的3维空间是主观的事情,因为对观测者的不同速度可以得到不同的分解。闵氏时空实现了一种客观的几何,不依赖于任何观测者的视点,而且不随观测者的改变而改变。从一定意义说,闵可夫斯基做的就是将“相对性”从狭义相对论中拿走,为我们呈现一幅绝对的时空活动的图景。
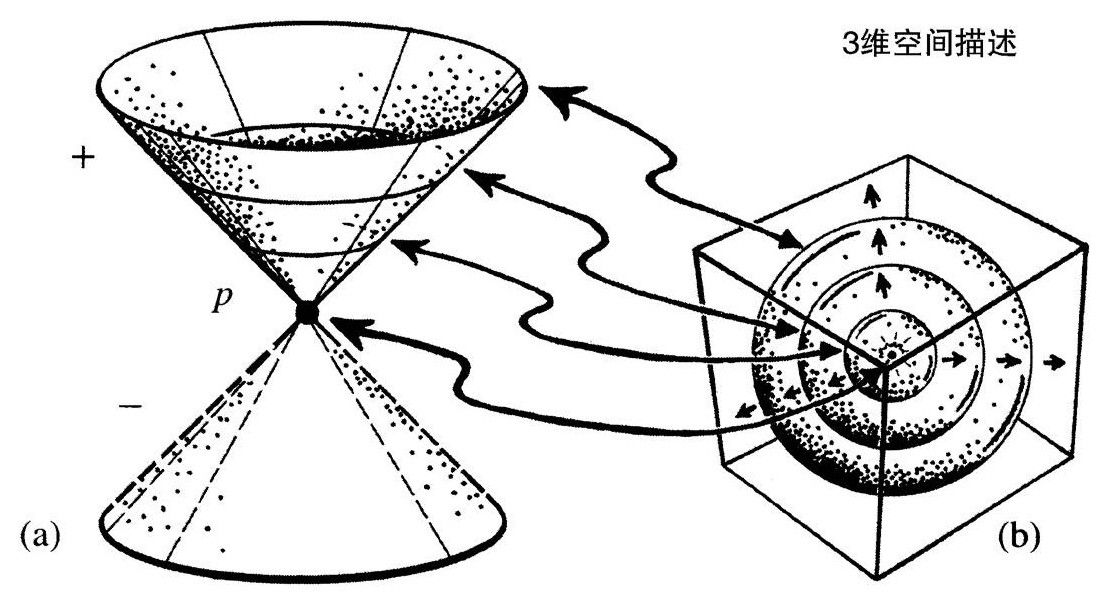
图2.12(a)闵氏4维空间中p的零锥;(b)未来锥的3维描述是原点在p的一系列膨胀的同心球
但是,为了得到一个严格的图景,我们需要一种4维空间的结构来取代随时刻不同的3维空间序列。什么结构呢?我用字母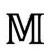 标记闵氏4维空间,闵可夫斯基为
标记闵氏4维空间,闵可夫斯基为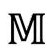 赋予的最基本几何结构是零锥的概念,[2.26]它描述
赋予的最基本几何结构是零锥的概念,[2.26]它描述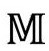 中任意事件p的光是如何传播的。零锥是一个双锥,有共同顶点p,它告诉我们在事件p的任意方向的“光速”是什么样的[见图2.12(a)]。手电筒为光锥提供了一个直观图像,起初它在内部聚光到事件p(过去零锥),然后从p向外扩展(未来零锥),犹如在p点爆发的闪光,因此爆发的空间的描述[图2.12(b)]就变成一系列膨胀的同心球面。在我的图中,我喜欢用相对垂线倾斜45°的锥面来画零锥,如果我们选择光速c=1的单位,就会得到这个图像。就是说,如果我们选择秒为时间尺度,那就选择光秒(=299792458米)为距离单位;如果选择年为时间尺度,那就选择光年(≈9.46×1012千米)为距离单位,等等。[2.27]
中任意事件p的光是如何传播的。零锥是一个双锥,有共同顶点p,它告诉我们在事件p的任意方向的“光速”是什么样的[见图2.12(a)]。手电筒为光锥提供了一个直观图像,起初它在内部聚光到事件p(过去零锥),然后从p向外扩展(未来零锥),犹如在p点爆发的闪光,因此爆发的空间的描述[图2.12(b)]就变成一系列膨胀的同心球面。在我的图中,我喜欢用相对垂线倾斜45°的锥面来画零锥,如果我们选择光速c=1的单位,就会得到这个图像。就是说,如果我们选择秒为时间尺度,那就选择光秒(=299792458米)为距离单位;如果选择年为时间尺度,那就选择光年(≈9.46×1012千米)为距离单位,等等。[2.27]
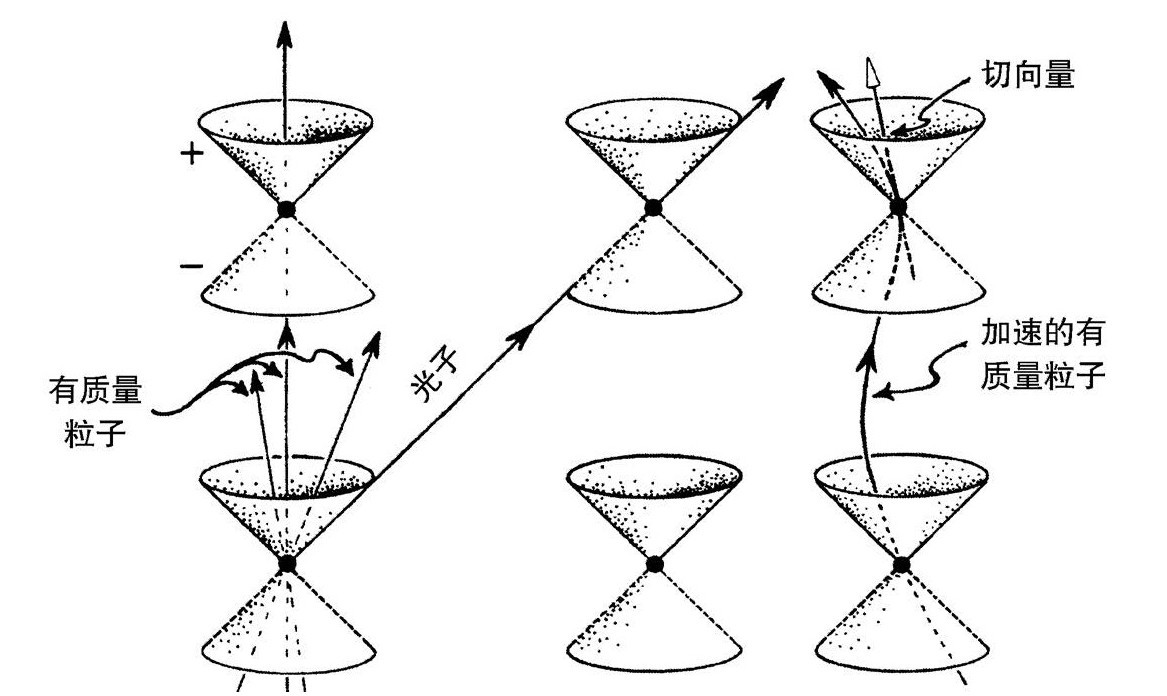
图2.1 3 中均匀分布的零锥。有质量粒子的世界线都引向锥的内部,而无质量粒子的世界线沿着锥的表面
中均匀分布的零锥。有质量粒子的世界线都引向锥的内部,而无质量粒子的世界线沿着锥的表面
爱因斯坦的理论告诉我们,任何有质量粒子的速度一定总是小于光速。用时空图来说,这意味着这种粒子的世界线——构成粒子历史的所有事件的轨迹——必然引向它的每个事件的零锥内部,如图2.13。粒子也可能在世界线的某些地方加速,那时它的世界线不会是直线;从时空图看,加速度表示为世界线的曲率。在世界线弯曲的地方,则世界线的切向量必然处于零锥内部。如果粒子无质量,[2.28]如光子,那么它的世界线必然沿着每一点的零锥的表面,因为它在每个事件中的速度其实就是光速。
零锥还向我们说明了因果性,因果性问题是确定哪些事件可能影响其他哪些事件。(狭义)相对论的一个原则是断言任何信号的传播都不允许比光还快。相应地,在 几何中,如果存在一条连接事件p和q的世界线,即从p到q的一条光滑路径位于零锥表面或内部,我们就说事件p能对事件q发生因果影响。为此,我们需要为路线确定一个均匀的从过去到未来的方向(即为路径加一个“箭头”)。这要求为
几何中,如果存在一条连接事件p和q的世界线,即从p到q的一条光滑路径位于零锥表面或内部,我们就说事件p能对事件q发生因果影响。为此,我们需要为路线确定一个均匀的从过去到未来的方向(即为路径加一个“箭头”)。这要求为 的几何赋予一个时间方向,相当于为每个零锥的两个部分分别赋予连续一致的“过去”和“未来”。我用“-”号标记每个过去零锥,用“+”号标记每个未来零锥,见图2.12(a)和图2.13,其中我用虚线来区分过去零锥。标准术语的“因果”指从过去到未来的因果影响,即它所在的世界线的定向切向量指向未来零锥的表面或内部。[2.29]
的几何赋予一个时间方向,相当于为每个零锥的两个部分分别赋予连续一致的“过去”和“未来”。我用“-”号标记每个过去零锥,用“+”号标记每个未来零锥,见图2.12(a)和图2.13,其中我用虚线来区分过去零锥。标准术语的“因果”指从过去到未来的因果影响,即它所在的世界线的定向切向量指向未来零锥的表面或内部。[2.29]

图2.14 广义相对论中的非均匀零锥
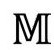 的几何是完全均匀的,每个事件都是平等的。但当我们过渡到爱因斯坦的广义相对论时,这种均匀性就普遍地失去了。不过,我们还可以为零锥赋予连续的时间方向,任何有质量粒子的世界线的未来方向的切向量仍然处于未来零锥内。而且,和前面一样,无质量粒子(光子)的世界线的切向量都沿着零锥表面。在图2.14中,我描绘了广义相对论的这种情形,其中零锥不再是均匀分布的。
的几何是完全均匀的,每个事件都是平等的。但当我们过渡到爱因斯坦的广义相对论时,这种均匀性就普遍地失去了。不过,我们还可以为零锥赋予连续的时间方向,任何有质量粒子的世界线的未来方向的切向量仍然处于未来零锥内。而且,和前面一样,无质量粒子(光子)的世界线的切向量都沿着零锥表面。在图2.14中,我描绘了广义相对论的这种情形,其中零锥不再是均匀分布的。
我们得试着想象这些锥画在某种印有零锥的理想“橡皮膜”上。我们可以在橡皮膜上任意活动,也能以任意方式扭曲它,只要变形是光滑的,零锥保持在膜上。我们的零锥决定了事件之间的“因果结构”,这是任何形变都改变不了的——只要我们认为橡皮膜一直带着这些锥。
2.1 节图2.3(c)的埃舍尔的双曲面呈现了类似的情景,在那儿我们可以想象埃舍尔的画就印在这种理想的橡皮膜上。我们可以让一个接近边界的魔鬼活动,通过这种变形,它来到先前被中心附近的魔鬼占据的位置。可以通过这种运动将所有的魔鬼移到先前被其他魔鬼占据的位置,而且这种运动也将描述埃舍尔图画表现的双曲几何的一种基本的对称性。在广义相对论中,这种对称性也会出现(和2.1节描述的弗里德曼模型一样),但是相当例外。然而,能够实现这种“橡皮膜”变形,正是广义相对论的基本组成部分,被称作“微分同胚”(或“一般坐标变换”)。关键是这种变形一点儿也不会改变物理状态。“一般协变性”原理作为爱因斯坦广义相对论的基石,所说的就是我们构建物理学定律时要用这种“橡皮膜变形”(“微分同胚”)的方式,它不会改变空间及其内容的物理意义和性质。
这并不是说所有几何结构都失去了,我们空间剩下的唯一几何或许就是它的拓扑性质之类的东西(实际上,拓扑学有时就被称为“橡皮膜几何”,它看茶杯的表面和环面是一样的,等等)。但我们必须用心确定需要什么结构。流形一词常用来描述这种有着确定有限维的空间(我们可以说有n个空间维的流形为n—流形),它是光滑的,但除了光滑和拓扑而外,不必赋予任何其他结构。在双曲几何的情形,流形其实还被赋予了度规的概念。度规是一个数学“张量”(见2.6节),常用字母g表示,可以认为它为空间中任何有限光滑的曲线赋予了长度。[2.30]构成这种流形的“橡皮膜”的任何变形都带着连接两点p, q的任何曲线(p,q也跟着变形),而度规g赋予的连接p和q的曲线段 的长度应该不受那种变形的影响(从这个意义说,g也是“跟着”变形走的)。
的长度应该不受那种变形的影响(从这个意义说,g也是“跟着”变形走的)。
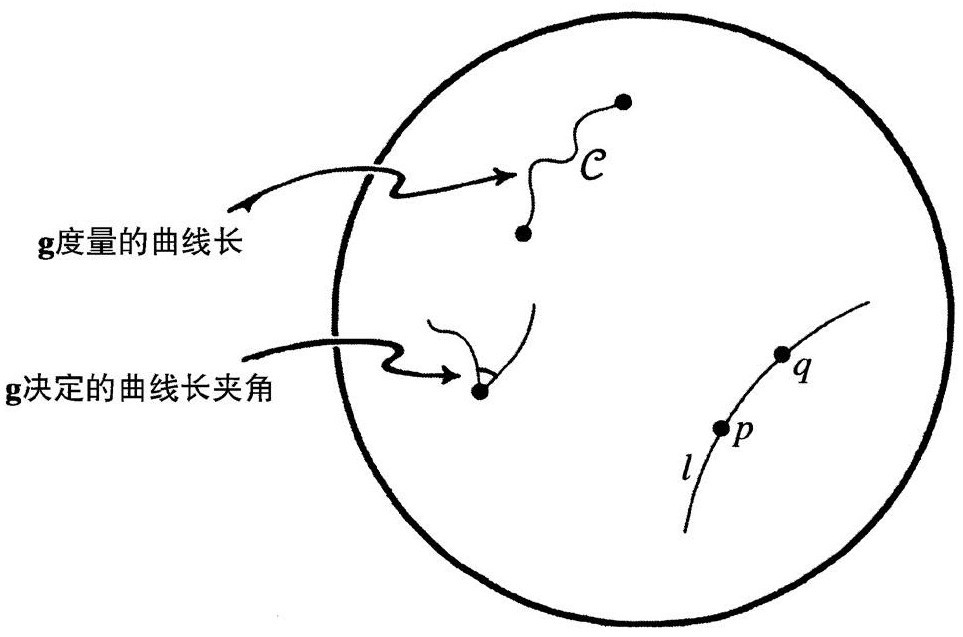
图2.15 度规g为曲线赋予长度和角度,测地线l提供了度规g下的“p和q点之间的最短路径”
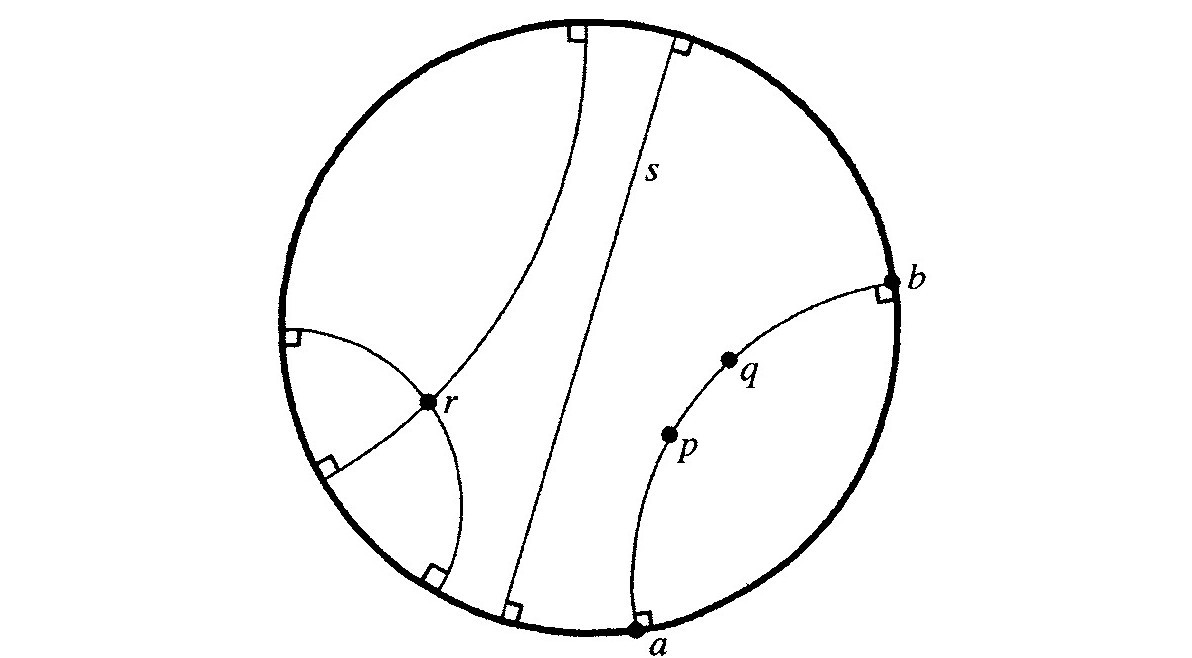
图2.16 在双曲面的共形表示中,“直线”(测地线)是与边界圆周交于直角的圆弧
长度概念还蕴涵着直线概念,即所谓的测地线,这种直线l的特征在于对线上的任意两个分离不太远的点p和q,从p到q的最短曲线(在g所赋予的长度意义上)实际上就等于l的pq部分的长度,见图2.15。(在这个意义上,测地线提供了“两点间的最短路径”。)我们还可以定义两条光滑曲线之间的角度(一旦g定了,这也就决定了),于是,当g给定时,我们也就有了普通的几何概念。不过,这个几何通常不同于我们熟悉的欧几里得几何。
于是,埃舍尔的双曲几何图像[图2.3(c),贝尔特拉米—庞家勒的共形表示]也有它的直线(测地线)。通过图形背景的欧几里得几何,这些测地线可以理解为与边界圆呈直角相交的圆弧(见图2.16)。令a和b是经过两个给定点p和q的弧线的端点,那么p和q之间的双曲g-距离等于
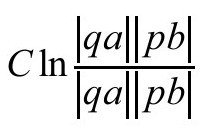
其中ln是自然对数(1.2节中常用对数lg的2.302585……倍),“|qa|”等代表背景空间的普通欧几里得距离,C是正常数,叫双曲空间的伪半径。
但是,我们可以不管g确定的结构而赋予某个其他类型的几何。我们这儿最关心的就是所谓的共形几何。这种结构可以度量两条光滑曲线在任一点相交的角度,但“距离”或“长度”的概念是不确定的。前面说过,角度的概念其实是由g决定的,但g本身却不能由角度概念来决定。虽然共形结构不能确定长度的量,却能决定任何一点处不同方向的长度之间的比值——所以它决定了无穷小的形状。我们可以将不同点的长度重新度量(放大或缩小)而不会改变共形结构(见图2.17)。我们记重新度量为

图2.17 共形结构不确定长度的度量,但通过任何一点在不同方向的长度之比确定了角度。长度可以在不同的点重新度量(放大或缩小),而不会影响共形结构
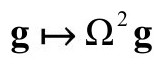
其中Ω是定义在每一点的正实数,在空间光滑变化。于是,不论Ω的取值如何,g和Ω2g决定了同一个共形结构,但g和Ω2g有不同的度规结构(如果Ω≠1),这里Ω是尺度变化因子。再看埃舍尔的图2.3(c),我们发现双曲面的共形结构(不是度规结构)其实等同于欧几里得空间在边界圆的内部,但不同于整个欧几里得平面的共形结构。
对我们的时空几何来说,这些思想仍然实用,但也有一些重要差别,原因在于闵可夫斯基对欧几里得几何概念的“扭曲”。这所谓“扭曲”就是数学家指的度规符号的改变。用代数的语言来说,其实就是几个“+”号变成了“-”号,它主要告诉我们,对n维空间来说,n个相互垂直的一组方向里,有多少被看作是“类时”的(在零锥内部),有多少是“类空”的(在零锥外面)。在欧几里得几何和它弯曲形式的黎曼几何中,我们认为所有方向都是类空的。“时空”的通常概念只包含一个类时方向,在这样的正交集中其余方向都是类空的。如果空间是平直的,我们称它为闵可夫斯基空间,如果空间是弯曲的,我们称它为洛伦兹(Lorentzian)空间。对我们考察的通常的时空类型(洛伦兹空间),n=4,符号是“1+3”,将我们的4个相互正交的方向分解为1个类时方向和3个类空方向。类空方向(或类时方向,假如多于1个)之间的“正交”意思是“交于直角”,而类空与类时方向之间的正交从几何上看更像图2.18描绘的情形,正交方向对称地与它们之间的零锥方向相连。从物理上讲,世界线沿类时方向的观测者认为在与他正交的类空方向发生的事件都是同时的。
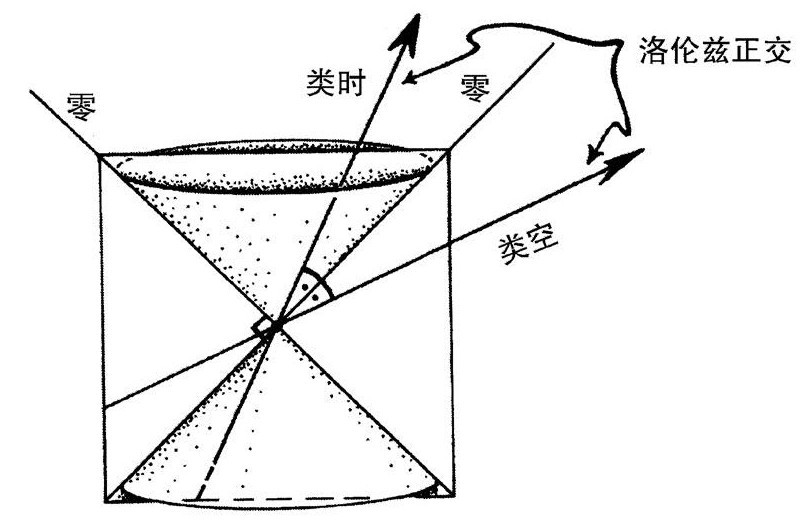
图2.18 欧几里得图像表示的类空和类时方向在洛伦兹时空里的“正交”,其中零锥是直角的
在寻常的(欧几里得或黎曼)几何里,我们惯于用空间间隔来考虑长度,而那间隔可以用一根直尺来度量。但在(欧几里得或黎曼)时空里,直尺是什么呢?是一根带子,乍看起来并不像用来测量两个事件p和q之间的空间间隔的东西,如图2.19。我们可以将p放到带子的一边,而把q放到另一边。我们还可以假定那个直尺很窄,而且没有加速,从而爱因斯坦广义相对论的(洛伦兹的)曲率效应就无关紧要,用狭义相对论就足以应对。但是根据狭义相对论,如果要直尺子度量的距离正确给出p和q之间的时空间隔,我们必须要求事件相对于直尺的静止坐标系是同时发生的。在直尺的静止坐标系中,我们如何确保事件真正是同时的呢?是啊,我们可以用爱因斯坦最初的论证方法。他更多的是用匀速运动的火车而不是直尺来思考——那么现在我们也那样来讨论。
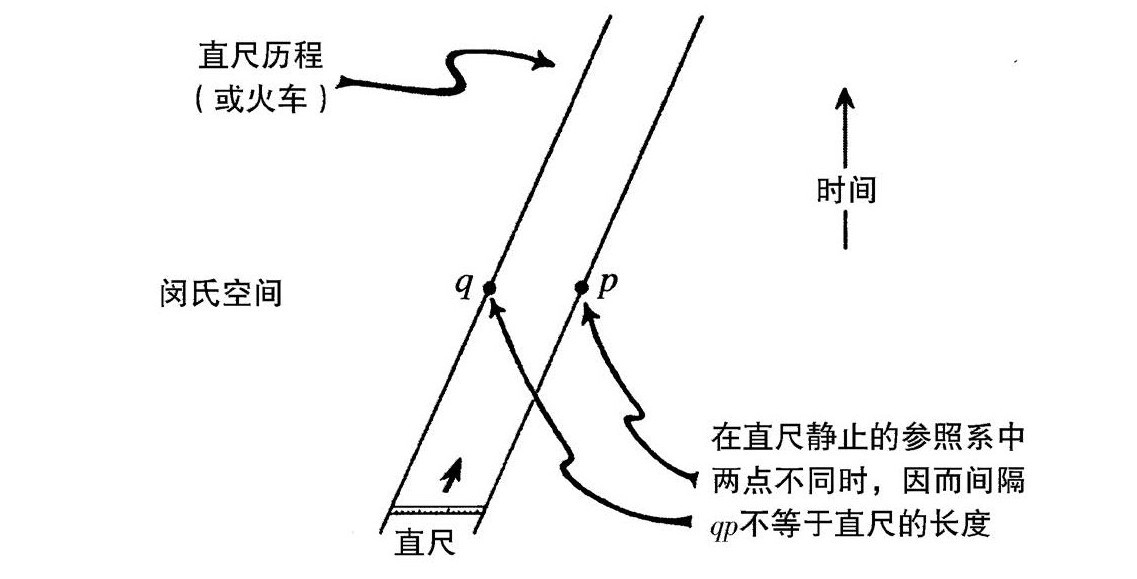
图2.19 点p和q在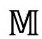 中的类空间隔不能直接用2维的带子来测量
中的类空间隔不能直接用2维的带子来测量
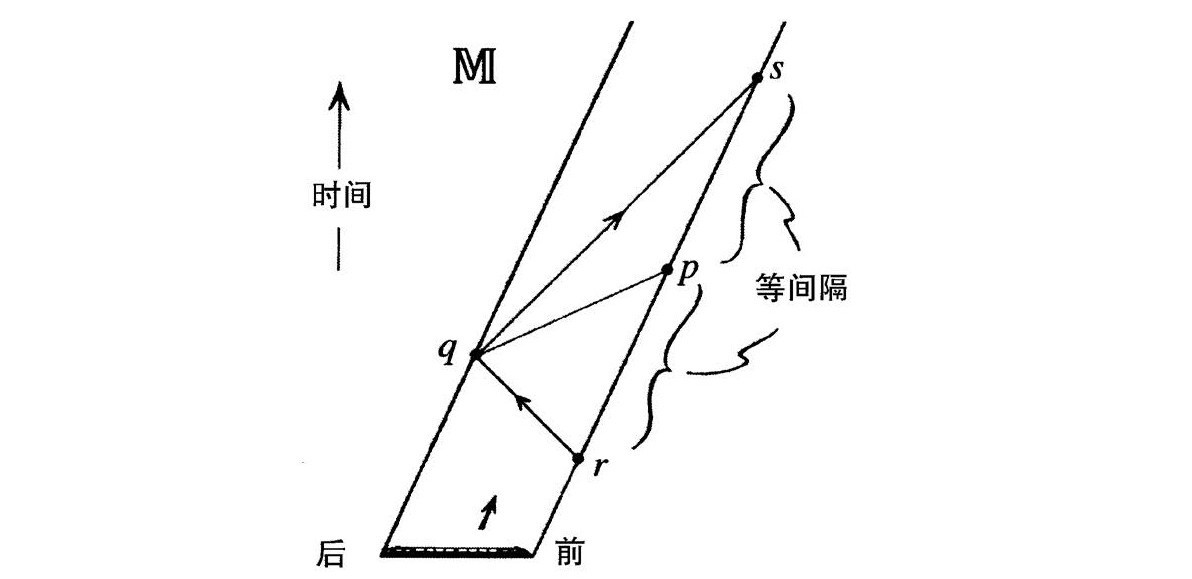
图2.20 只有当p q同时,火车(直尺)才能度量距离p q,所以我们需要光信号和时钟
令发生事件p的火车(直尺)的一端为车头,而q的一端为车尾。想象车头有一个观测者,从事件r向车尾发出一个光信号,达到那儿的时刻恰好发生事件q;信号立刻反射回车头,在事件s被观测者接收,见图2.20。于是,假如p在发射和接收信号的中间时刻,即从r到p的时间间隔恰好等于从p到s的时间间隔,那么观测者可以判断q与p在火车的静止坐标系里是同时的。这时(也仅仅在这时),火车(即直尺)的长度恰好等于p和q的空间间隔。
我们看到,这不但比简单“拿尺子”量两个事件的空间间隔要复杂一些,而且观测者实际测量的是时间间隔rp和ps。这些(相等的)时间间隔直接提供了我们需要确定的空间间隔pq的度量(用光速为1的单位)。这说明了时空度量的关键事实,即它更多的是与时间(而非距离)的测量有着直接的关系。它不是度量曲线的长度,而是直接为我们提供时间的度量。而且,被赋予时间度量的并非都是曲线:只有所谓的因果曲线才可能是粒子的世界线,这些曲线处处是类时的(切向量在零锥内部,是有质量粒子的路径)或零的(切向量沿着零锥表面,是无质量粒子的路径)。时空度规g的作用是为任何因果曲线的有限线段赋予时间度量(对零曲线的任何部分,时间度量的贡献为零)。在这个意义上,正如著名爱尔兰相对论专家辛格(John L.Synge)建议的[2.31],时空度规具有的“几何”不是“测地”(geometry)的,而是“测时的”(“chronometry”)。
因为整个理论依赖于以自然方式定义的度规g,[2.32]所以对广义相对论的物理学基础来说,重要的是大自然真的存在基本水平的超精确时钟。实际上,这个时间度量对物理学来说也是相当核心的问题,因为我们可以明确地说,任何一个(稳定的)有质量粒子都充当着几乎完美的时钟。如果粒子质量为m(假定是常数),那么我们从爱因斯坦的著名公式可以看到它有一个静止能量E:[2.33]
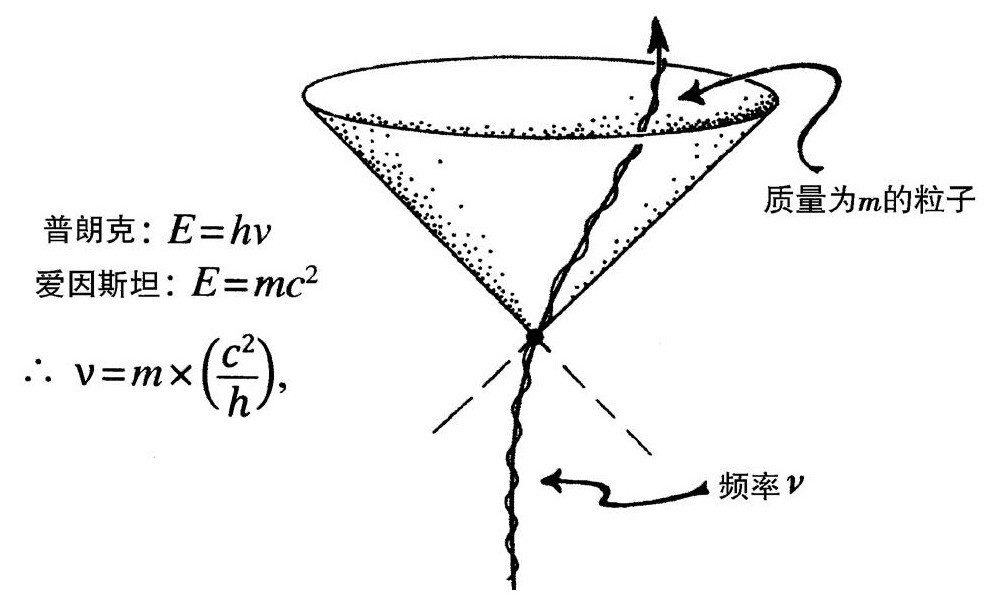
图2.21 任何稳定的有质量粒子的行为犹如一个非常精确的量子钟
E=mc2
这是相对论的基本结果。另一个几乎同样著名的公式——量子论的基本公式——是普朗克公式
E=hν
(h是普朗克常数),它告诉我们粒子的静止能量定义了一个特别的量子振动的频率ν(见图2.21)。换句话说,任何稳定的有质量粒子的行为犹如一个非常精确的量子钟,它“滴答”的特定频率恰好正比于它的质量,系数为基本常数c2/h:
ν=m(c2/h)
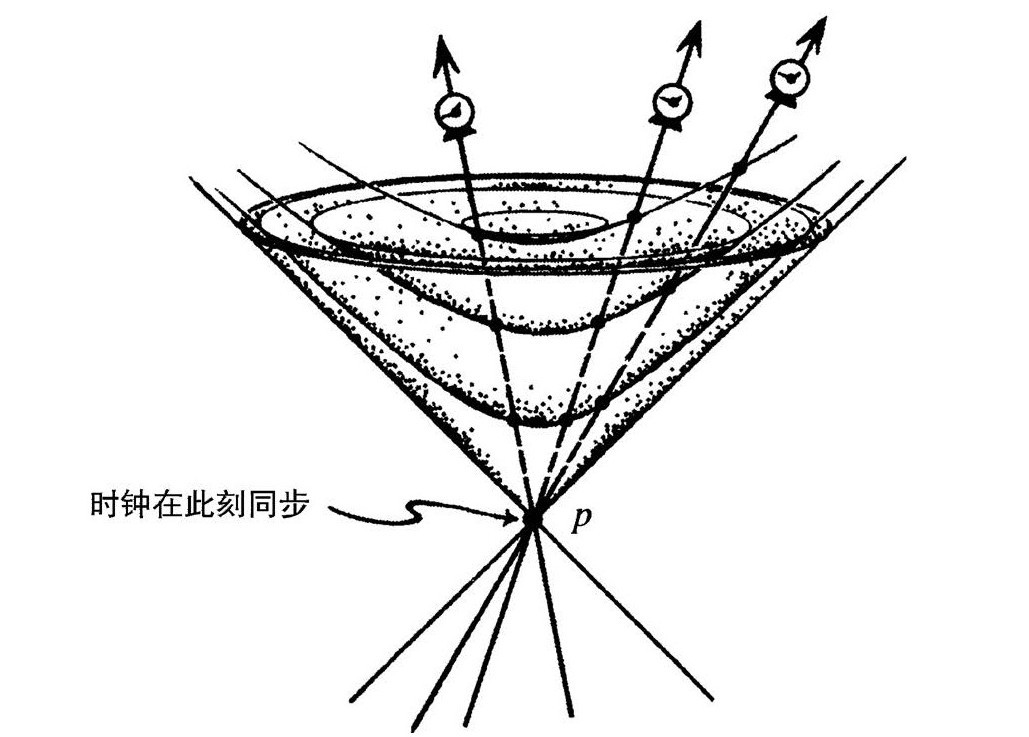
图2.22 碗型3维曲面代表同样时钟的不同瞬间
实际上,单个粒子的量子频率是极高的,不可能直接用来做实用的时钟。对实际的时钟来说,我们需要一个包含大量粒子的系统,众粒子结合起来协同作用。但关键的一点还在于我们做钟是需要质量的。单凭无质量粒子(如光子)是不可能做出时钟来的,因为它们的频率只能是零;光子要等到永恒才可能让它内在的“时钟”敲响第一声“滴答”!这个事实对我们以后有着重大意义。
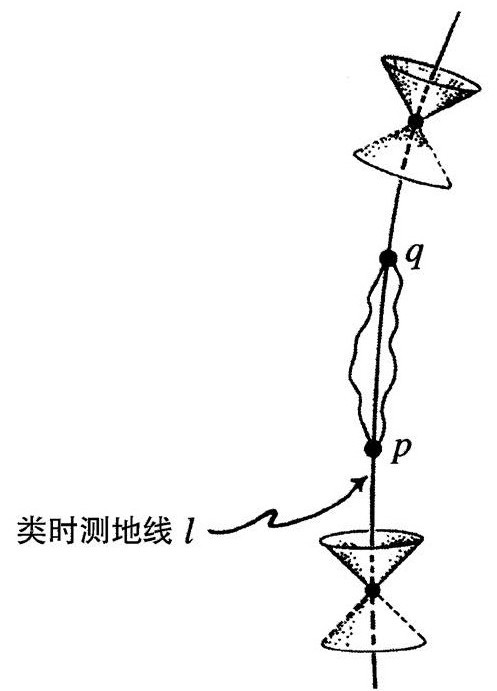
图2.23 类时测地线l的特征在于,对l上的任何两个间隔不太远的点p和q,从p到q的最长局域曲线其实就是l的那部分长度
这些都遵从图2.22,我们可以从它看到不同的时钟——都从同一个事件p出发,但以不同速度(堪比光速但小于光速)运动。碗型的3维曲面(普通几何中的双曲面)区分了相同时钟的一串“滴答”。(这些3维曲面是闵氏几何球面的类比,是到固定点的“距离”为常数的曲面。)我们注意,因为无质量粒子的世界线是沿着零锥的,它连第一个碗型曲面都不可能达到,这和我们前面说的是一致的。
最后,类时曲线的测地线概念在物理上可以解释为有质量粒子在引力作用下的自由运动的世界线。在数学上,类时测地线l的特征表现为,对l上任意两个分隔不太远的点p和q,从p到q的最长曲线(在g决定的时间长度的情况下)其实就是l的一部分,见图2.23——它奇妙地倒转了测地线的欧几里得或黎曼空间的长度极小性质。这种测地概念也适用于零测地线,这种情形的“长度”为零,单凭时空的零锥结构就能确定。这种零锥结构其实等价于时空的共形结构,这个事实对我们以后有重要意义。
2.4 黑洞与时空奇点
在多数物理情形,引力效应都相对较弱,零锥只是略微偏离它在闵氏空间
的位置。然而对黑洞来说,正如我想在图2.24说明的,情形就大为不同了。这个时空图像代表超大质量(大约是太阳质量的10倍或更多)星体的坍缩,它在耗尽内部能源(核能)之后,会不可阻挡地向内坍缩。在一定时刻——可以认为是星体表面的逃逸速度达到光速的时刻——零锥向内倾斜到极端情形,[2.34]几乎使未来锥的最外面部分在图中竖立起来。跟踪这些特殊锥体的外缘,我们可以划定一个3维曲面,即所谓的事件视界——进入它的星体将一直落下去。(当然,我画图的时候不得不压缩一个空间维,所以视界看起来是一个2维曲面,但这应该不会迷惑读者。)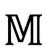 因为零锥的倾斜,我们看到从事件视界内部发出的任何粒子的世界线或光信号不可能跑到视界外面,因为穿过视界会违背2.3节的要求。另外,假如在远离黑洞的安全地方有个观测者在遥望黑洞,如果追溯(逆着时间)进入他眼睛的光线,我们会发现光线不可能穿过视界进入内部,而只能飘浮在世界曲面的上空,恰好在星体陷入视界的瞬间到达它。不管外面的观测者等待多长时间(即不管我们的图像距离观测者多远),理论上总是这样的。但在实际上,观测者感觉的图像是高度红移的,而且会迅速(从观测者的时间看)从他的眼前消失,从而图像会在瞬间变得漆黑——成为名副其实的“黑洞”。
因为零锥的倾斜,我们看到从事件视界内部发出的任何粒子的世界线或光信号不可能跑到视界外面,因为穿过视界会违背2.3节的要求。另外,假如在远离黑洞的安全地方有个观测者在遥望黑洞,如果追溯(逆着时间)进入他眼睛的光线,我们会发现光线不可能穿过视界进入内部,而只能飘浮在世界曲面的上空,恰好在星体陷入视界的瞬间到达它。不管外面的观测者等待多长时间(即不管我们的图像距离观测者多远),理论上总是这样的。但在实际上,观测者感觉的图像是高度红移的,而且会迅速(从观测者的时间看)从他的眼前消失,从而图像会在瞬间变得漆黑——成为名副其实的“黑洞”。
我们自然要问:星体向内落下的物质在穿过视界之后会怎么样呢?也许它会卷入某种复杂的运动,旋转着落到中心的附近,然后反弹回来?这样的坍缩模型(如图2.24),原来是奥本海默(J.Robert Oppenheimer)和他的学生斯尼德(Hartland Snyder)在1939年提出的,它还代表了爱因斯坦方程的一个精确解。然而,为了以确定的方式表示这个解,他们不得不做了些简化的假定。其中最重要(也最严格)的是必须假定精确的球对称,这样就不能表示非对称的物质“旋转”;他们还假定星体的物质特性可以合理地近似为无压力流体——即相对论理论家们所说的“尘埃”(参见2.1节)。奥本海默和斯尼德发现,在这些假定下,向内的坍缩会一直持续下去,直到中心点的物质密度成为无限大,相应的时空曲率也变成无限大。于是,他们的解出现的那个中心点——图2.24中用波浪线表示——被称为时空奇点,爱因斯坦理论在那儿“崩了”,而标准的物理学也没有办法进一步推演这个解。
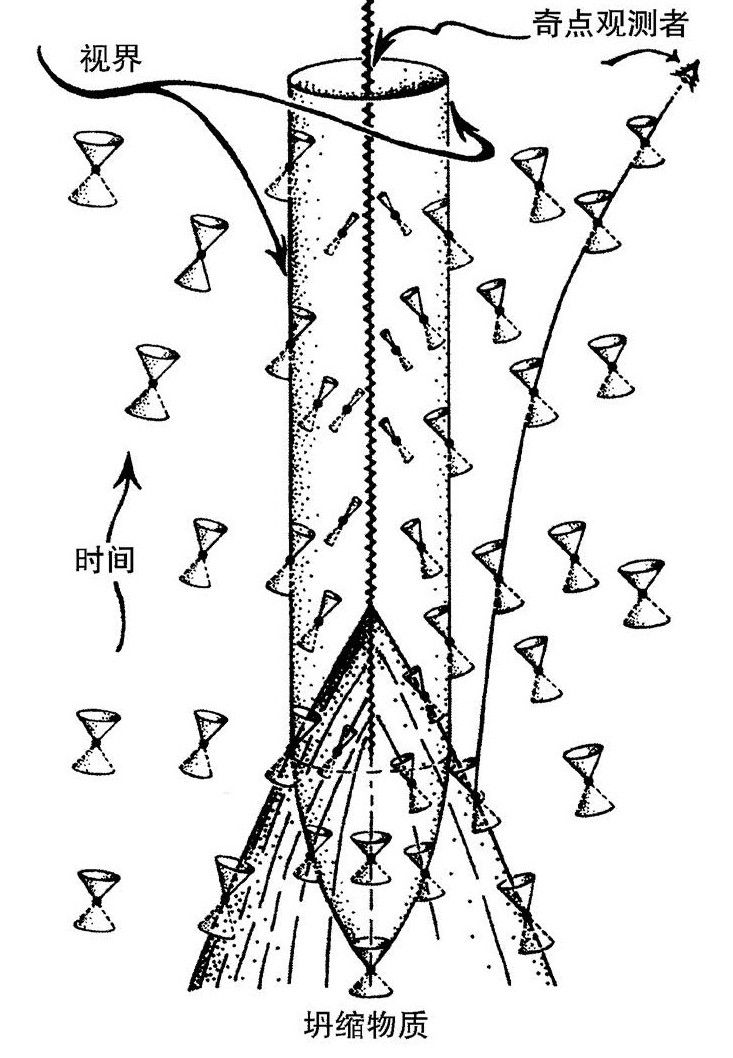
图2.24 超大质量星体坍缩成黑洞。当未来锥向内的倾斜在图中竖起时,来自星体的光不可能逃出它的引力。这些锥的包络就是事件视界
这些时空奇点的存在给物理学家提出了根本性的难题,通常被看作宇宙大爆炸起源的逆问题。如果说大爆炸为时间的开始,那么黑洞里的奇点就代表时间的终结——至少就最终落入黑洞的那些物质来说是这样的。在这个意义上,我们可以说黑洞奇点呈现的问题也就是大爆炸所呈现的时间反演问题。
每一条从视界内部发出的因果曲线(如图2.24的黑洞坍缩图像),在尽可能向未来延伸时,一定会终结于中心黑洞,这是真的。同样,在2.1节说的任何弗里德曼模型中,每一条因果曲线(整个模型中)如果尽可能向过去延伸,必然会终结(其实是起源)于大爆炸奇点。于是,除了黑洞情形更有局域性而外,两种情形实际上是互为时间反演的。不过,我们的第二定律也意味着这不可能都是正确的。与我们在黑洞遇到的境况相比,大爆炸肯定是处于某种极低熵的状态。一个事物与它的时间反演之间的区别,肯定是我们这儿要考虑的一个关键问题。
在讨论这种区别的性质(2.6节)之前,我们还必须面对一个基本问题。我们必须弄清楚我们是否真有理由或在什么程度上相信那些模型——一个是奥本海默和斯尼德的模型,另一个是像弗里德曼那样的高度对称的宇宙学模型。我们必须注意奥本海默—斯尼德引力坍缩图像的两个重要的基本假定,即球对称假定和物质的特别理想化——将构成坍缩体的物质当作完全无压力的。这两个假定也适用于弗里德曼宇宙学模型(球对称更适用于所有FLRW模型),所以我们有理由怀疑,在如此极端情形下,这些理想化模型是否一定能代表坍缩物质遵从爱因斯坦广义相对论的必然行为。
实际上,当我在1964年秋开始认真思考引力坍缩问题时,就萦绕着这两个问题。那时,施密特(Maarten Schmidt)刚发现一种令人瞩目的天体,它极端的光亮和多变意味着它可能有什么性质接近我们现在所说的“黑洞”的东西。接着,思想深邃的美国物理学家惠勒(John A.Wheeler)向我表达了他的担心,我就是在他的激发下考虑那些问题的。当时,大家根据苏联物理学家栗弗席兹(Evgeny Mikhailovich Lifshitz)和卡拉尼科夫(Markovich Khalatnikov)的一些具体理论工作,普遍相信在一般情形下(即对称性条件不适用),通常的引力坍缩不会出现时空奇点。我对俄罗斯人的工作只有模糊了解,但我怀疑他们用的那种数学分析方法能得出任何决定性的结论,所以我开始用自己的更几何的方法来考虑这个问题。[2.35]这需要认识各种整体性的特征,如光线如何传播,它们如何在时空中聚焦,当它们开始卷曲并相互穿过时会出现什么样的奇异曲面?
我以前用这些方法考虑过与稳恒态宇宙模型(2.2节开头介绍的)有关的问题。我很喜欢那个模型(但喜欢的程度不如爱因斯坦的广义相对论)——特别是它把基本的时空几何概念与基本的物理学原理美妙地统一起来了——我好奇的是,有没有可能把两者相互协调起来。如果我们坚持光滑的稳恒态模型,立刻就会发现,假如不引进负能量密度,是不能达成和谐的。在爱因斯坦理论中,负能量的效应是生出分离的光线,以对抗正常物质的正能量密度的向内弯曲的效应(见2.6节)。一般说来,负能量在物理系统的出现是一个“坏消息”,因为它可能导致不可控制的不稳定性。所以我想知道,对称的偏离是否可能避免这种令人不快的结果。然而,可用于描述这类光线曲面的拓扑行为的整体分析是强大有力的,如果小心运用,它们可以用于更一般的情形,能导出和对称性假设一样的结论。要点在于(尽管我从未发表这些结果),对对称性的合理偏离并没有真正的作用,所以稳恒态模型,即使允许远离对称的光滑模型,也不可能避免与广义相对论发生冲突,除非出现负能量。
我也用过一些同样类型的论证,考察当我们考虑引力系统的遥远未来时会出现的不同可能性。指引我的方法涉及共形时空几何(2.3节,在第3部分将发挥重要作用),也引导我去思考一般情形的光线系统[2.36]的聚焦性质。于是我开始相信我对那些东西相当熟悉了,就把注意力转向引力坍缩问题。主要的新问题是我们需要某种标准来刻画坍缩在哪些情形经过了“不归点”,因为在很多情形下物体的坍缩可以反转——当压力变得足以抵抗坍缩时,物质会“反弹”回来。“不归点”似乎出现在视界形成的时候,那时引力已变得强大无比,会吸引所有东西。然而,从数学上确定视界的出现和位置却是费力不讨好的事情,其精确定义实际上需要我们考察它在无穷大的行为。这时候,我幸运地冒出一个想法[2.37]——即“俘获曲面”的概念——它有着很强的局域特征,[2.38]它在时空的出现可以作为发生无限引力坍缩的条件。
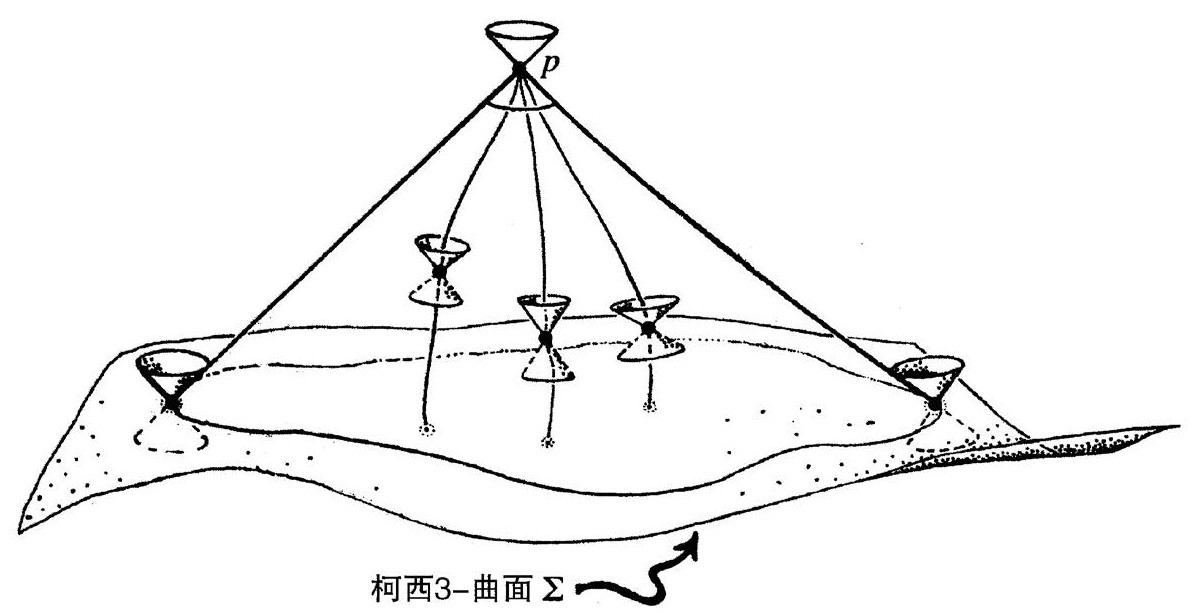
图2.25 初始柯西(Cauchy)曲面Σ:在它未来的任何一点p都有这样的性质:终结于p的每条因果曲线向过去延伸足够远时,总会与这个曲面相遇
运用我发展的这种“光线/拓扑”论证方法,我接着证明了一个定理,[2.39]大概意思说,不论引力坍缩什么时候发生,只要时空满足几个“合理的”条件,奇点都是不可避免的。条件之一是,光线的聚合不能是负的。更物理地说,这意味着如果假定了爱因斯坦方程(不管有无宇宙学常数Λ),那么穿过光线的能量流就不能是负的。第二个条件是,整个系统必须从开放的(即所谓“非紧致的”)类空3维曲面Σ开始演化。对合理的局域的(即非宇宙学尺度的)物理演化情形来说,这是一个非常标准的条件。从几何上说,我们的要求等于是我们所考虑的时空中任何向Σ的未来演化的因果曲线,在尽可能向后(时间上)延伸时,必然与Σ相交(图2.25)。其他唯一的要求(除了存在俘获面的假定)则关乎“奇点”在这个情景下到底是什么意思。根本说来,奇点其实就是一个障碍,它阻碍着时空光滑地向无限未来延伸,[2.40]与刚才的假定一致。
这个结果的力量在于它的普适性。它不仅不需要对称性假定,也不需要任何其他求解方程的简化条件;它只要求将引力场的物质源性质限制为“物理上合理的”,即根据物理学要求,通过任何光线的能量流绝不能是负的——这就是有名的“弱能量条件”。奥本海默和斯尼德,还有弗里德曼假定的无压力尘埃当然满足这个条件。但情形比这些普遍得多,它包括相对论学家们考虑的各种类型的物理现实的经典物质。
然而,结果尽管很有力量,也有弱点,对坍缩星体所面临的问题的性质,它几乎什么也没说。它没有提供任何有关奇点几何形式的线索,甚至没以任何其他方式告诉我们物质会达到无限大密度,或者时空曲率终将成为无穷。而且,它也没告诉我们奇点行为会从哪儿开始显现出来。
为弄清这些问题,我们还需要做一些事情,大概类似于前面说的俄罗斯物理学家栗弗席兹和卡拉尼科夫的具体分析。不过我在1964年年底发现的定理似乎与他们先前的断言相冲突!实际上正是如此,在后来的几个月出现了很多惊恐和混乱。不过,就在那时,俄罗斯人在年轻同事别林斯基(Vladimir A.Belinski)帮助下找到并修正了他们先前工作的错误,问题也就迎刃而解了。他们原先认为爱因斯坦方程的奇点解只是一个非常特殊的情形,修正的工作则与我获得的结果一致,证明奇点行为其实是一种普遍现象。而且,别林斯基—卡拉尼科夫—栗弗席兹的工作为奇点研究提供了一种极端复杂的混沌行为的可能情形,现在叫BKL猜想。根据美国相对论理论家米斯纳(Charles W.Misner)的考虑,我们早已预言了那种行为——即所谓的搅拌机宇宙——在我看来,这种狂野而混沌的“搅拌机”行为,至少在很大一类可能的条件下是一种普遍情形。
关于这个问题,我以后还要谈(2.6节),不过现在我们必须说明另一个问题,即俘获面之类的事情,是否真的可能发生在任何合理的情形中?超大质量星体在演化的最后阶段可能灾难性地坍缩,提出这个预言的最初理由来自钱德拉塞卡(Subrahmanyan Chandrasekhar)1931年的研究,他发现像白矮星(第一个已知的例子是明亮的天狼星的那颗神秘暗淡的伴星)那样的小尺度致密星体,质量与太阳接近,但半径和地球差不多。令白矮星维持的是电子简并压力——这是量子力学原理的一个效应,能阻止电子拥塞在一起。钱氏证明,如果考虑(狭义)相对论效应,能以这种方式抗拒引力的星体存在一个质量极限,极限质量大约是1.4M⊙(M⊙代表太阳质量);他还注意到,这给超过这个“钱氏极限”的冷物质带来了巨大难题。
像我们太阳那样的寻常星体(“主序星”)的演化,有那么一个晚期阶段,它的外层会膨胀,从而变成一颗红巨星,并伴随生成一个电子简并核。这个核逐渐聚集越来越多的星体物质,假如结果不超过钱氏极限,那么整个星体将终结为一颗白矮星,最终冷却为黑矮星。其实,这也是我们太阳注定的命运。但是对更大的星体,如果超过了钱氏极限,白矮星核可能在某个阶段坍缩,向内坠落的物质将导致极端暴烈的超新星爆炸(也许能连续几天照亮它所在的整个星系)。这个过程可能释放足够多的物质,从而生成的核可以维持在更高的密度(例如1.5M⊙的物质压缩到直径大约10千米的区域),形成一颗中子星,这是由中子简并压力维持的星体。
中子星有时表现为脉冲星(见2.1节和那儿的注释),迄今在银河系里已经观测到了很多。但这种星体仍然存在一个可能质量的极限,大约为1.5M⊙[有时称朗道(Landau)极限]。如果原来的星体有足够大的质量(例如大于10M⊙),那么在爆炸中,很可能没有足够的物质发射出去,留下的核心也不可能保持为中子星,于是没有东西能阻止它的坍缩,最终将达到一个时刻,形成俘获面。
当然,这不是确定的结论,我们也可以说,对俘获面形成(尽管只有中子星半径的三分之一)之前物质达到的那种极端致密状态,我们的认识还不够充分。然而,黑洞的情形要强得多,想想吧,它可是在大得多的尺度上把星系中心附近的星体都聚集起来了。那个空间足以容纳(例如)一百万颗白矮星,它们不必实际接触,占据着直径大约为106千米的区域,要在它们周围形成俘获面,这个尺度是足够小了。就黑洞的形成来说,极端高密度下“未知物理”的问题并不是真的很要紧。
到现在为止,我隐藏了一个更深刻的理论问题。我一直是未加说明地假定了俘获面的存在蕴涵着黑洞的形成,然而,这个推论依赖于所谓的“宇宙监督”——尽管它赢得了广泛的承认,但迄今仍是一个未经证实的猜想。[2.41]它和BKL猜想一样,可能是经典广义相对论的主要未解问题。宇宙监督说的是,在一般的引力坍缩中,不可能出现裸露的时空奇点。这儿“裸露”的意思是从奇点出发的因果曲线可以跑出来到达外面远处的观测者。(于是奇点能被外面的观测者看见,而没有被视界遮蔽。)我在2.6节还会再来讨论宇宙监督。
不管怎么说,如今的观测形势非常支持黑洞的存在。某些双星系统包含着几倍太阳质量的黑洞,其证据就很令人信服,尽管它多少有点儿“负”特征:系统的不可见成员的存在,是通过动力学运动显现的;而不可见成员的质量远大于任何致密天体根据标准理论所能具有的质量。这类观测中最令人惊奇的是,那颗看得见的星体围绕着银河系中心的一个看不见但质量巨大的物体高速运动着,运动速度之快,要求那个隐藏的天体必须具有大约4000000M⊙的质量!除了黑洞而外,很难想象它还能是别的什么东西。除了这种“负”的证据,我们还观测到了具备这种性质的其他天体,它们在拖曳着周围的物质,而物质似乎并没有为那个天体加热一个“表面”。不存在有形的表面正是黑洞存在的直接证据[2.42]。
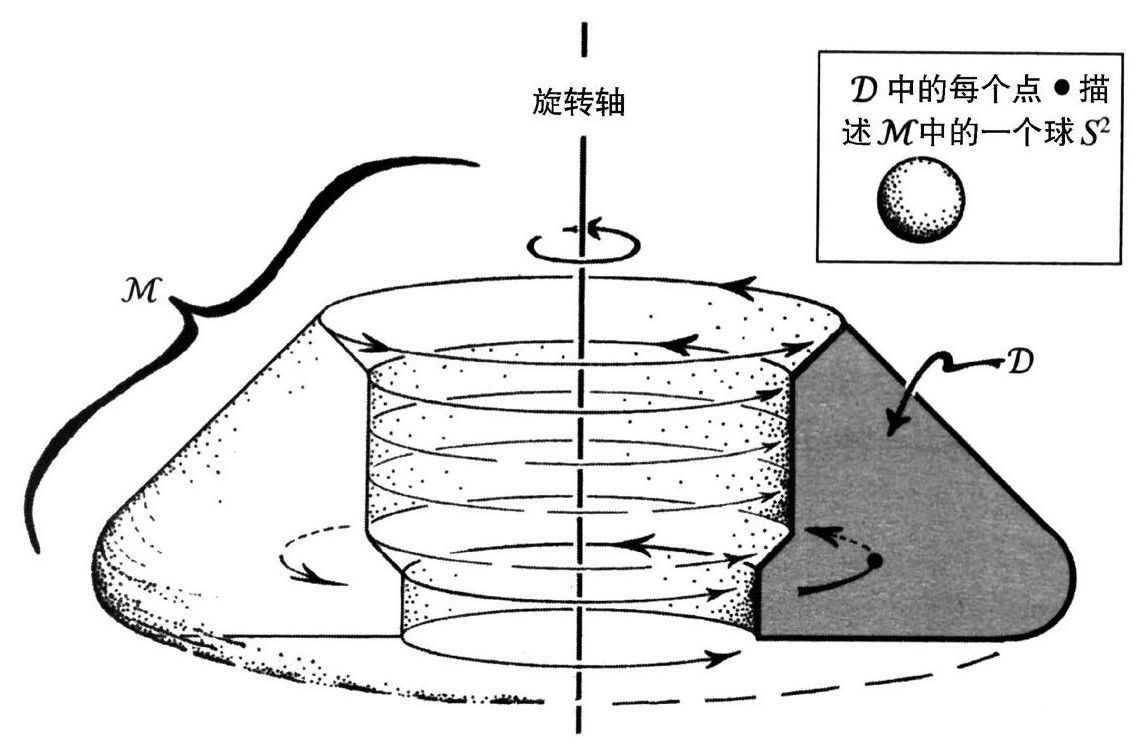
图2.26 用以表示具有精确球对称的时空(这儿记为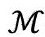 )的严格共形图
)的严格共形图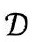 。2维区域
。2维区域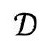 旋转(通过2维球面S2)生成4维空间
旋转(通过2维球面S2)生成4维空间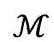
图2.27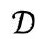 边界的虚线是一个对称轴,每一点代表一个时空点而不是一个球面S2
边界的虚线是一个对称轴,每一点代表一个时空点而不是一个球面S2
2.5 共形图与共形边界
有一种便捷的方法可以表示整个时空模型,特别是当模型具有球对称性时,例如在奥本海默—斯尼德和弗里德曼时空的情形。那就是用共形图。我在这儿要区分两类共形图:严格的共形图和概略的共形图。[2.43]我们会看到每种图的用途。
我们从严格的共形图说起,它可以用来表示具有严格球对称的时空(这儿记为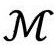 )。这种图是平面上的一个区域
)。这种图是平面上的一个区域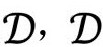 内部的每个点代表
内部的每个点代表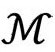 中的一整个球(即S2)的点。为了得到有用的图像,我们可以舍去一个空间维,想象将
中的一整个球(即S2)的点。为了得到有用的图像,我们可以舍去一个空间维,想象将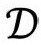 绕着左边的某条垂线旋转(图2.26)——那条线叫旋转轴。于是,
绕着左边的某条垂线旋转(图2.26)——那条线叫旋转轴。于是,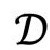 的每一点转出一个圆周(S1)。这个图对我们的直观想象来说足够清楚了,但对我们时空
的每一点转出一个圆周(S1)。这个图对我们的直观想象来说足够清楚了,但对我们时空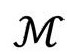 的整个4维图像来说,我们需要一个2维旋转,这样每个
的整个4维图像来说,我们需要一个2维旋转,这样每个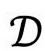 内的点将转出
内的点将转出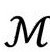 中的一个球(S2)。
中的一个球(S2)。
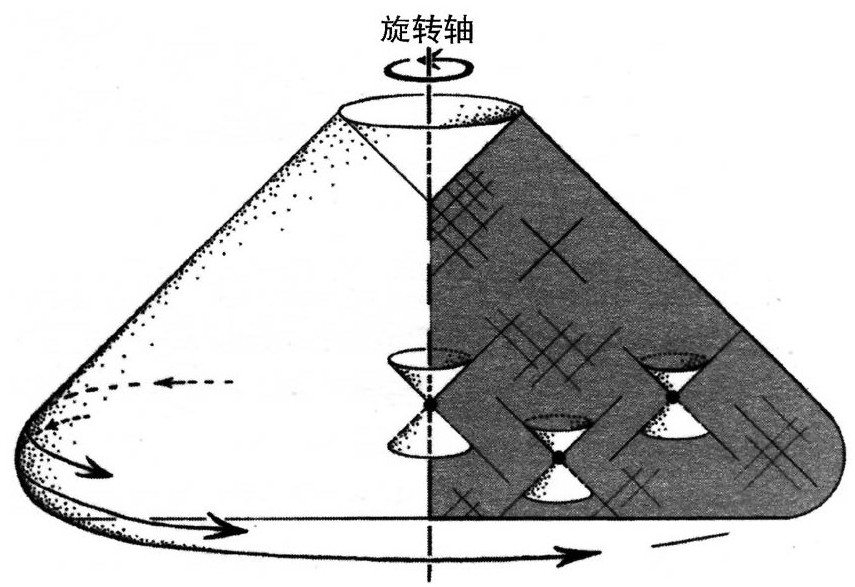
图2.28  中倾斜45°的零锥是
中倾斜45°的零锥是 中的零锥与嵌入
中的零锥与嵌入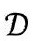 的交集
的交集
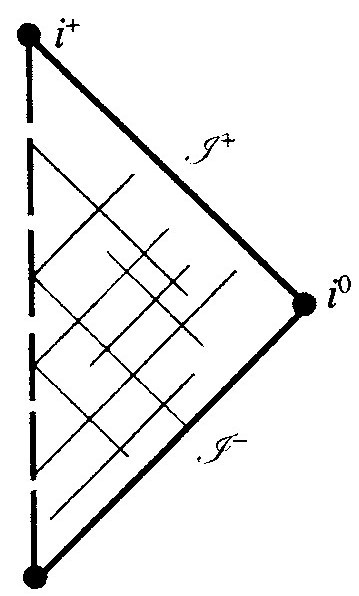
图2.29 闵可夫斯基空间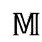 的严格共形图
的严格共形图
在严格共形图中,我们通常会看到一个旋转轴,它是区域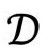 的边界的一部分。于是,轴上的那些边界点——在图中用虚线表示——每一个都代表4维时空的单个点(而不是一个S2),从而整条虚线代表
的边界的一部分。于是,轴上的那些边界点——在图中用虚线表示——每一个都代表4维时空的单个点(而不是一个S2),从而整条虚线代表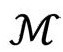 中的一条线。图2.27让我们看到整个时空
中的一条线。图2.27让我们看到整个时空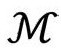 是如何由一族等同于
是如何由一族等同于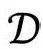 绕虚线轴旋转的2维空间构成的。
绕虚线轴旋转的2维空间构成的。
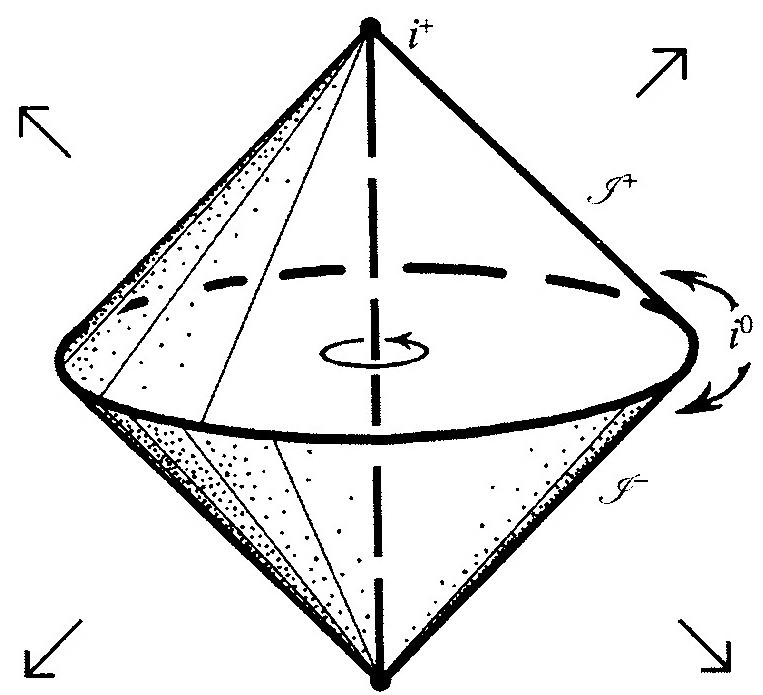
图2.30 为得到闵氏时空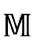 的正常图形,想象把倾斜的(锥)边界无限外推
的正常图形,想象把倾斜的(锥)边界无限外推
我们将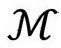 视为共形时空,而不太关心为
视为共形时空,而不太关心为 赋予整个度规g的特殊尺度。这样,正如2.3节最后一句说的,
赋予整个度规g的特殊尺度。这样,正如2.3节最后一句说的,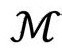 被赋予了一族(时间定向的)零锥。与此相应的是,
被赋予了一族(时间定向的)零锥。与此相应的是,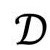 本身作为
本身作为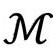 的2维子空间,从它继承了2维共形空间结构,而且具有自己的“时间定向零锥”。这就在
的2维子空间,从它继承了2维共形空间结构,而且具有自己的“时间定向零锥”。这就在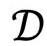 的每一点构成了一对不同的“零”方向,指向时间的未来。(它们恰好是确定
的每一点构成了一对不同的“零”方向,指向时间的未来。(它们恰好是确定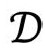 的复本的平面与
的复本的平面与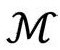 的未来零锥的相交线,见图2.28。)
的未来零锥的相交线,见图2.28。)
在严格的共形图中,我们尽量将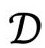 中所有未来零锥的方向调整到与垂向呈45°。为说明这种情形,我在图2.29中画出了整个闵氏时空
中所有未来零锥的方向调整到与垂向呈45°。为说明这种情形,我在图2.29中画出了整个闵氏时空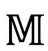 的共形图,径向零线也画成与垂向呈45°。在图2.30中,我说明了这个图是怎么画出来的。我们看到,图2.29表现了共形图的一个重要特征:尽管把整个无限时空
的共形图,径向零线也画成与垂向呈45°。在图2.30中,我说明了这个图是怎么画出来的。我们看到,图2.29表现了共形图的一个重要特征:尽管把整个无限时空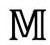 都包容在内了,图形却只是一个有限的(直角)三角形。实际上,共形图的特征就是,它们能将无限的时空区域“压缩”到有限的图形里。无限远本身也能在图中表现出来。两条粗斜的边界线分别代表过去零无限远
都包容在内了,图形却只是一个有限的(直角)三角形。实际上,共形图的特征就是,它们能将无限的时空区域“压缩”到有限的图形里。无限远本身也能在图中表现出来。两条粗斜的边界线分别代表过去零无限远 和未来零无限远
和未来零无限远 ;
;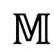 中的每一条零测地线(零直线)必然在
中的每一条零测地线(零直线)必然在 上有一个过去端点,而在
上有一个过去端点,而在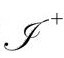 上有一个未来端点。(字母
上有一个未来端点。(字母 通常读scri,意思是“手写
通常读scri,意思是“手写 ”。)[2.44]边界上还有3个点:i-,i0,i+,分别代表过去类时无限远、类空无限远、未来类时无限远,
”。)[2.44]边界上还有3个点:i-,i0,i+,分别代表过去类时无限远、类空无限远、未来类时无限远,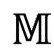 的每一条类时测地线都一定有过去端点i-和未来端点i+,每一条类空测地线则通过i0闭合成圈。(我们很快会看到,为什么i0必须认为只是一个单点。)
的每一条类时测地线都一定有过去端点i-和未来端点i+,每一条类空测地线则通过i0闭合成圈。(我们很快会看到,为什么i0必须认为只是一个单点。)
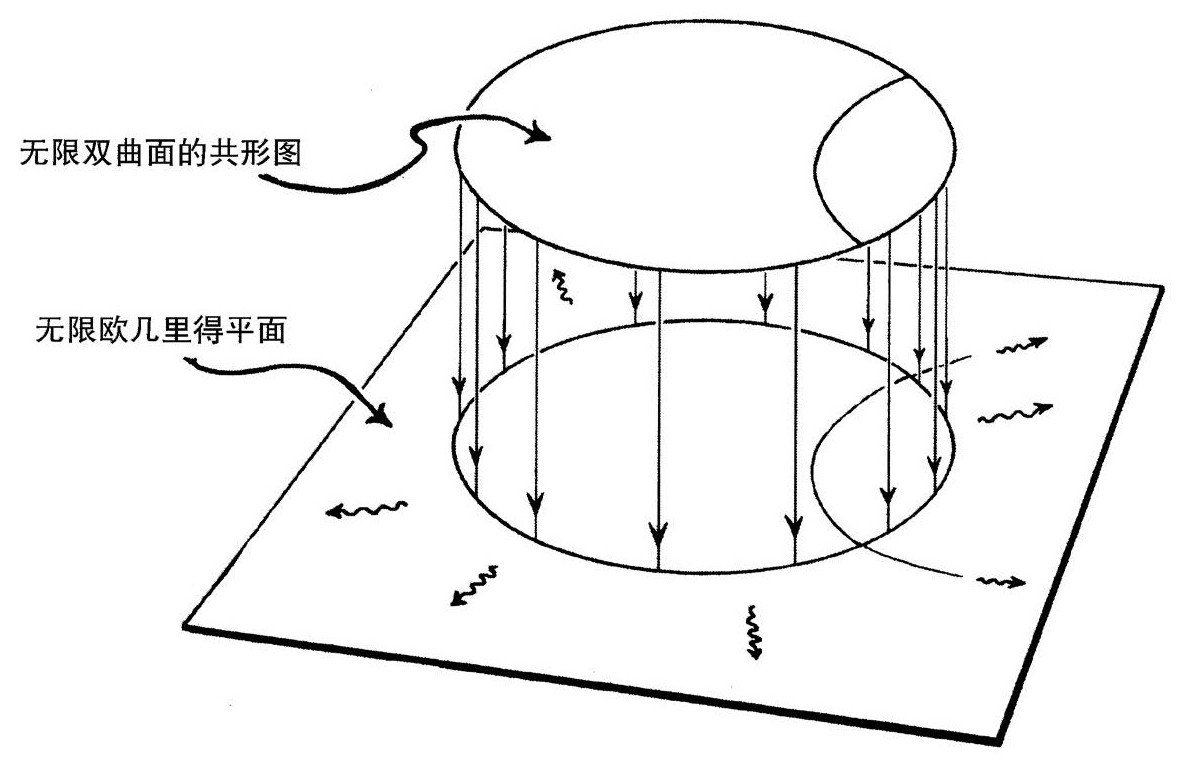
图2.31 将光滑共形流形的双曲面延伸到它在欧氏平面的共形边界之外

图2.32(a)爱因斯坦宇宙的直观图(“爱因斯坦柱”);(b),(c)同一宇宙的严格共形图
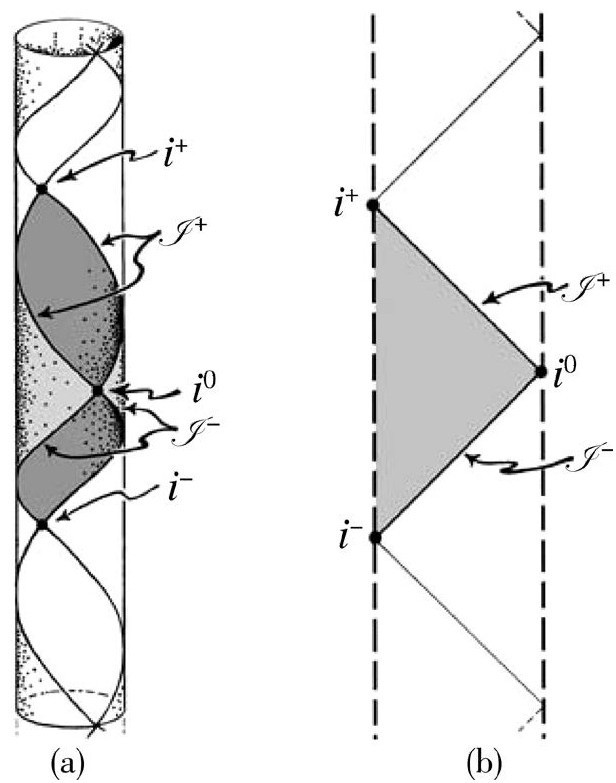
图2.33 说明为什么i0是单点
(a)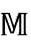 呈现为
呈现为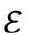 的共形子区域,整个
的共形子区域,整个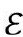 可以看成由
可以看成由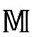 空间的无限序列共形构成;(b)以严格共形图说明(a)是如何实现的
空间的无限序列共形构成;(b)以严格共形图说明(a)是如何实现的
这时我们回想一下埃舍尔的版画是有好处的。图2.3(c)描绘了整个双曲面的共形图。边界圆以共形的方式代表它的无限远,本质上类似于前面 一起代表
一起代表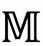 的无限远。其实,正如可以把光滑共形流形的双曲面扩展到它在欧几里得平面中的共形边界之外(图2.31),我们也可以光滑地将
的无限远。其实,正如可以把光滑共形流形的双曲面扩展到它在欧几里得平面中的共形边界之外(图2.31),我们也可以光滑地将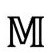 扩展为边界之外的更大共形流形。实际上,
扩展为边界之外的更大共形流形。实际上,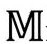 共形等价于我们称为爱因斯坦宇宙学
共形等价于我们称为爱因斯坦宇宙学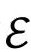 的时空模型(又叫“爱因斯坦柱”)的一部分。这是一个空间3维球(S3)的全静态的宇宙学模型。图2.32(a)是模型的直观图像(为实现这个模型,爱因斯坦在1917年第一次引进了他的宇宙学常数Λ;见2.1节),图2.32(b)则代表它的严格共形图。注意,图中有两个分离的“旋转轴”(垂直虚线表示)。这完全是一致的,我们只是认为图中每一点所代表的S2随着靠近虚线而收缩到零。这也可以解释一个貌似奇怪的事实:
的时空模型(又叫“爱因斯坦柱”)的一部分。这是一个空间3维球(S3)的全静态的宇宙学模型。图2.32(a)是模型的直观图像(为实现这个模型,爱因斯坦在1917年第一次引进了他的宇宙学常数Λ;见2.1节),图2.32(b)则代表它的严格共形图。注意,图中有两个分离的“旋转轴”(垂直虚线表示)。这完全是一致的,我们只是认为图中每一点所代表的S2随着靠近虚线而收缩到零。这也可以解释一个貌似奇怪的事实: 的空间无限远从共形来看恰好是单点i0,因为它原来代表的S2的半径已经收缩到零了。时空
的空间无限远从共形来看恰好是单点i0,因为它原来代表的S2的半径已经收缩到零了。时空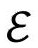 的空间截面S3就从这个过程显露出来。图2.33(a)说明了
的空间截面S3就从这个过程显露出来。图2.33(a)说明了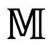 如何作为
如何作为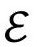 的共形子区域而出现,其实这也说明了我们如何能在共形意义上,将整个流形
的共形子区域而出现,其实这也说明了我们如何能在共形意义上,将整个流形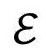 视为由
视为由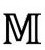 的无限序列所构成,其中每个
的无限序列所构成,其中每个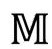 的
的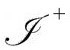 与下一个
与下一个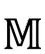 的
的 相接;图2.33(b)说明了这是如何通过严格共形图实现的。记住这个图对我们考虑第3部分提出的模型大有好处。
相接;图2.33(b)说明了这是如何通过严格共形图实现的。记住这个图对我们考虑第3部分提出的模型大有好处。
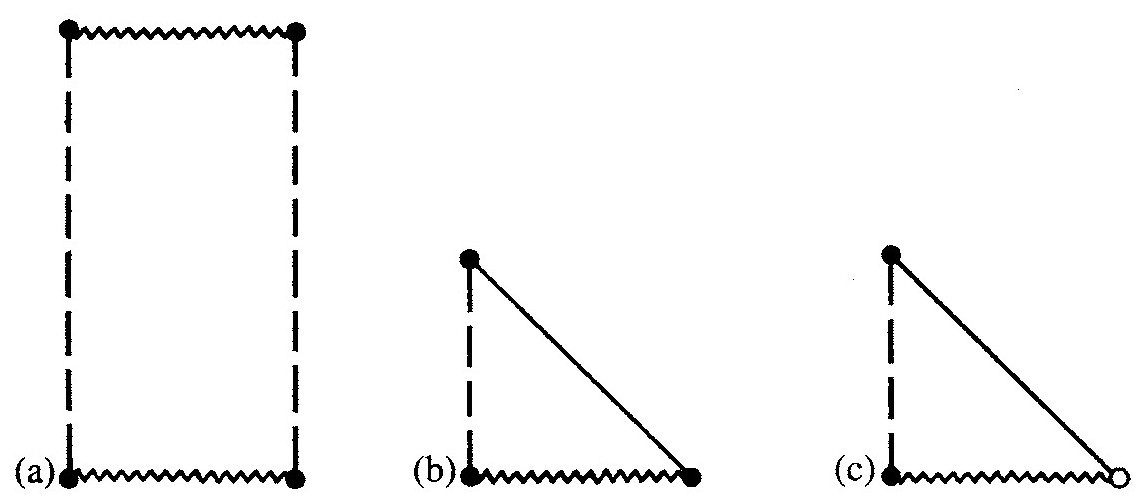
图2.34 Λ=0的弗里德曼宇宙学的三种不同情形的严格共形图:(a)K>0,(b)K=0,(c)K<0。
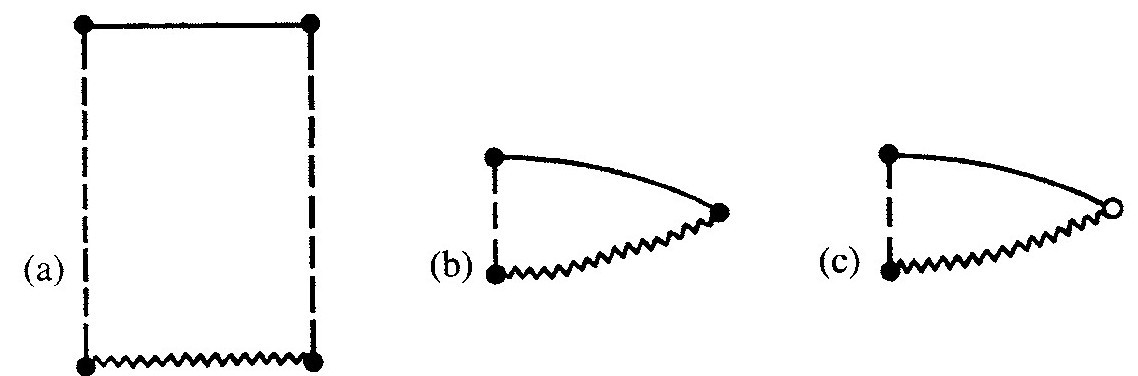
图2.35 Λ>0的弗里德曼宇宙学的三种不同情形的严格共形图:(a)K>0,(b)K=0,(c)K<0
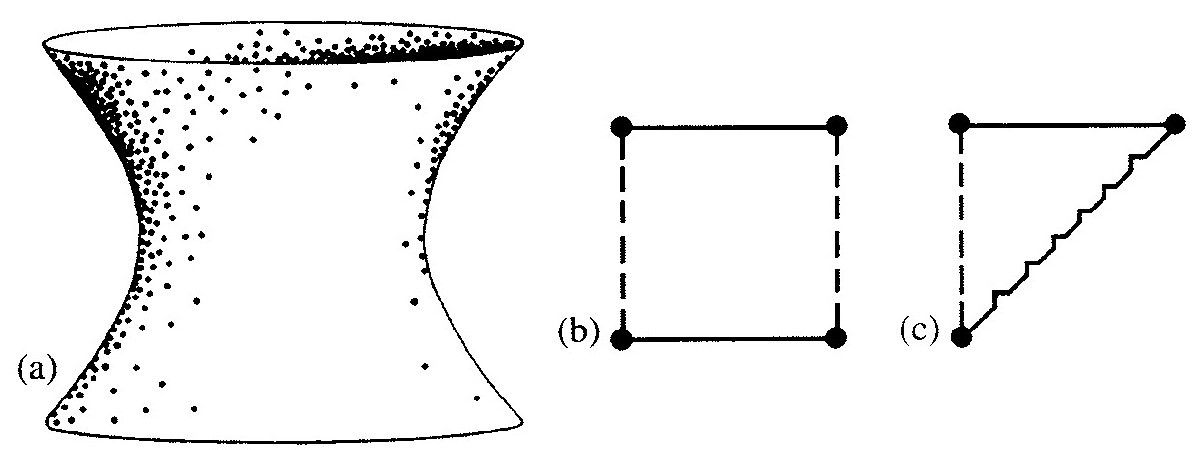
图2.36 德西特时空:(a)闵氏三维空间内的表示(压缩了2个空间维);(b)它的严格共形图;(c)截取一半,我们得到稳恒态模型的严格共形图
现在我们考虑2.1节介绍过的弗里德曼宇宙学。图2.34(a),(b),(c)分别描绘了Λ=0的3种不同情形:K>0,K=0,K<0。在这儿,奇点由波浪线代表。我还引进了一个记号,边界上的小白点“〇”代表整个球S2,而黑点“●”代表单点(在 的情形已经有过了)。在埃舍尔用过的2维情形的共形表示中,小白点其实代表双曲空间的边界球。对应的正宇宙学常数的情形(Λ>0,当K>0时,我们假定空间曲率不能超过Λ而引起最终的再次坍缩),如图2.35(a),(b),(c)。这儿应该指出这些图的一个重要特征。这些模型的未来无限远
的情形已经有过了)。在埃舍尔用过的2维情形的共形表示中,小白点其实代表双曲空间的边界球。对应的正宇宙学常数的情形(Λ>0,当K>0时,我们假定空间曲率不能超过Λ而引起最终的再次坍缩),如图2.35(a),(b),(c)。这儿应该指出这些图的一个重要特征。这些模型的未来无限远 是类空的,正如最终边界线所示,总是比45°方向更水平,正与Λ=0情形下出现的未来无限远相反[如图2.34(b),(c)和图2.29],在那儿边界为45°,所以
是类空的,正如最终边界线所示,总是比45°方向更水平,正与Λ=0情形下出现的未来无限远相反[如图2.34(b),(c)和图2.29],在那儿边界为45°,所以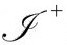 是零超曲面。这就是宇宙学常数的数值与
是零超曲面。这就是宇宙学常数的数值与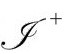 的几何本性之间的关系所具有的特征,对我们的第3部分有重要意义。
的几何本性之间的关系所具有的特征,对我们的第3部分有重要意义。
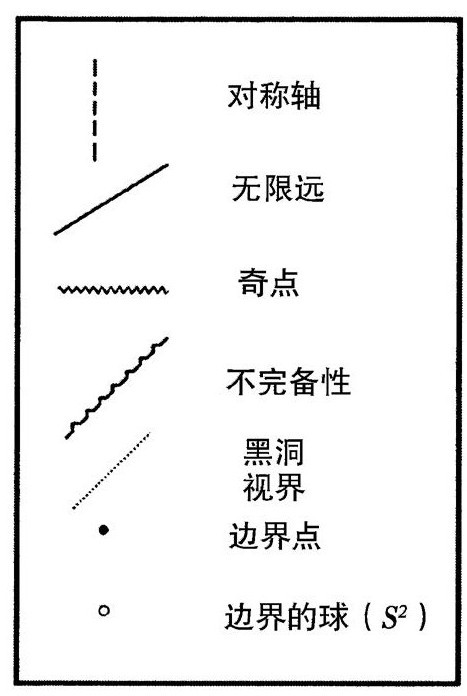
图2.37 严格共形图符号说明
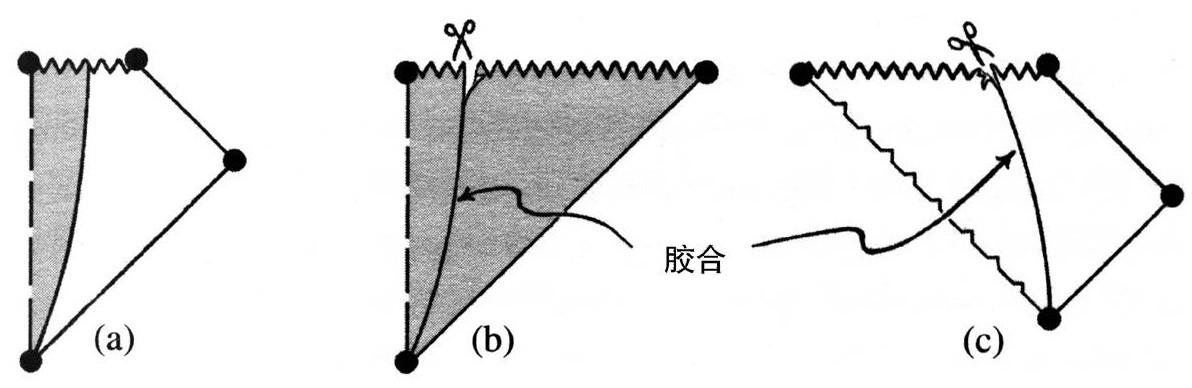
图2.38 向黑洞坍缩的奥本海默-斯尼德模型:(a)通过胶合构造的严格共形图;(b)弗里德曼模型(图2.34b)时间反演的左半部分;(c)爱丁顿—芬克尔斯坦模型(图2.39b)的右边部分
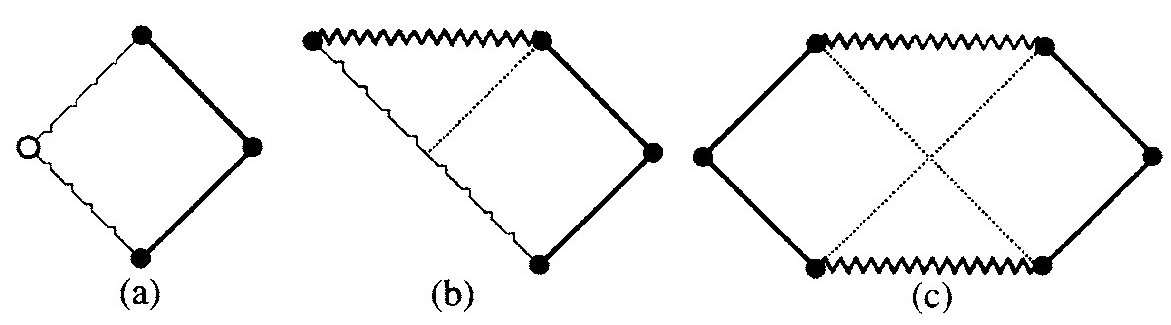
图2.39 球对称真空(Λ=0)的严格共形图:(a)原始史瓦西解(史瓦西半径以外);(b)推广到爱丁顿-芬克尔斯坦坍缩度规;(c)完全推广到克鲁斯卡/辛格/塞克尔形式
Λ>0的弗里德曼模型在遥远未来(接近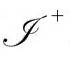 )都表现为近似的德西特(de Sitter)时空
)都表现为近似的德西特(de Sitter)时空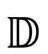 。这个模型宇宙完全没有物质而且是高度对称的(是4维的闵可夫斯基类比)。在图2.36(a)中,我画了一个
。这个模型宇宙完全没有物质而且是高度对称的(是4维的闵可夫斯基类比)。在图2.36(a)中,我画了一个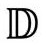 的2维图形,它只有一个空间维(全德西特4维空间
的2维图形,它只有一个空间维(全德西特4维空间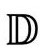 应该是5维闵氏空间里的超曲面);在图2.36(b)中,我还画出了它的严格的共形图。正如图2.36(c)中所示的,我们在2.2节说过的稳恒态模型,只是
应该是5维闵氏空间里的超曲面);在图2.36(b)中,我还画出了它的严格的共形图。正如图2.36(c)中所示的,我们在2.2节说过的稳恒态模型,只是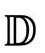 的一半。因为要把
的一半。因为要把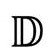 “切开”,所以稳恒态模型实际上就是我们所说的在过去方向“不完全的”。也就是说,存在那样的普通类时测地线——代表有质量粒子的自由运动——其时间度量不能延伸到某个有限数值以外的更早时刻。如果用于未来方向,这也可以认为是模型的恼人缺陷,因为它可以用于某个粒子或空间旅行者的未来,[2.45]但我们在这儿只说那种粒子运动根本不会出现。
“切开”,所以稳恒态模型实际上就是我们所说的在过去方向“不完全的”。也就是说,存在那样的普通类时测地线——代表有质量粒子的自由运动——其时间度量不能延伸到某个有限数值以外的更早时刻。如果用于未来方向,这也可以认为是模型的恼人缺陷,因为它可以用于某个粒子或空间旅行者的未来,[2.45]但我们在这儿只说那种粒子运动根本不会出现。
不论以什么观点来看那种不完备性的物理,我在严格共形图中都用小锯齿线来表示它。在我的严格共形图中,还用了一种点线,代表黑洞的事件视界。我在图中会一直用5种线条(对称轴的虚线、无限远的实线、奇点的波浪线、不完备性的锯齿线和黑洞视界的点线)和两种点(黑点代表4维空间的单点,白点代表S2),如图2.37的说明。
图2.38(a)画的是奥本海默—斯尼德的向黑洞坍缩的严格共形图,它是把坍缩的弗里德曼模型的一部分与爱丁顿—芬克尔斯坦(Eddington-Finkelstein)推广的史瓦西(Schwarzschild)解“胶合”起来的结果,如图2.38(b),(c)及图2.39的严格共形图。史瓦西求解爱因斯坦方程是在1916年,那时广义相对论方程刚发表。他的解描述了一个静态的球对称物体(如星体)外的引力场,可以向内推广(作为静态时空)到史瓦西半径
2MG/c2
其中M是物体的质量,G是牛顿引力常数。对地球来说,半径大约为9厘米,而太阳为3千米——但在这些情形,半径深埋在天体内部,只是一个与时空几何没有直接关系的理论距离,因为史瓦西度规只适用于物体外的区域。见图2.39的严格共形图。
然而对黑洞来说,史瓦西半径在视界处。在这个半径,度规的史瓦西形式会出现奇点,而史瓦西半径起初就被认为是时空的真实奇点。但是,勒梅特(Georges Lemaitre)在1927年首先发现,如果我们放弃时空静态的要求,就能以连续光滑的方式扩展那个解。1930年,爱丁顿发现了更简单的扩展方式(尽管他忘了指出得到了什么)。1958年,芬克尔斯坦重新发现了这种描述,并且明确指出了它的意义,其严格共形图如图2.39(b);这个共形图表现了所谓“史瓦西解的最大扩展”。图2.39(c)通常叫克鲁斯卡—塞克尔(Kruskal-Szekeres)扩展,尽管辛格(J.L.Synge)[2.46]早就发现了更复杂的描述。
图2.40 黑洞的霍金蒸发
图2.41 霍金黑洞蒸发的严格共形图
在3.5节,我们将看到黑洞的另一个特征,尽管现在微不足道,最终却是至关重要的。据霍金(Stephen Hawking)在1974年的分析,[2.47]根据爱因斯坦广义相对论的经典物理,黑洞应该是全黑的,但如果在弯曲时空背景下加入量子场论效应,黑洞应该具有非常低的温度T,与黑洞的质量成反比。例如,对一个10M⊙的黑洞,温度大约是6×10-9K,堪比MIT(麻省理工学院)2006年前在实验室达到的最低温度纪录——10-9K。今天我们周围的黑洞大约就是这样的温度。黑洞越大越冷,我们银河系中心的质量约4000000M⊙的黑洞,温度只有1.5×10-14K。如果拿CMB的温度作为我们宇宙此刻的环境温度,就温暖得多了,约为2.7K。
不过,如果从漫长的观点看,而且别忘了宇宙的指数式膨胀(如果无限继续下去)会大大冷却CMB,我们相信它会降到可能出现的最大黑洞的温度。然后,黑洞开始向周围空间辐射它的能量,而失去能量必然失去质量(根据爱因斯坦的E=mc2);当它失去质量时,会越变越热,经过一个难以置信的漫长时期(对眼下的最大黑洞来说,也许是10100——即一个googol——年)之后,它将完全收缩,最终“砰然一声”消失——这最后的爆炸几乎不能称为“爆炸”,因为它可能只有一颗小子弹的能量,不过强弩之末的一丝气力!
当然,这是把我们现有的物理知识和理解大大地外推了。不过,霍金的分析符合我们接受的一般原理,而那些原理似乎意味着整个结论是在所难免的。于是,我接受了它作为对黑洞最终命运的一种可能解释。实际上,这个预期将构成我在本书最后提出的纲领的重要组成部分。不管怎么说,在这儿画出这个过程的草图(图2.40)和它的严格共形图(图2.41),还是有意义的。
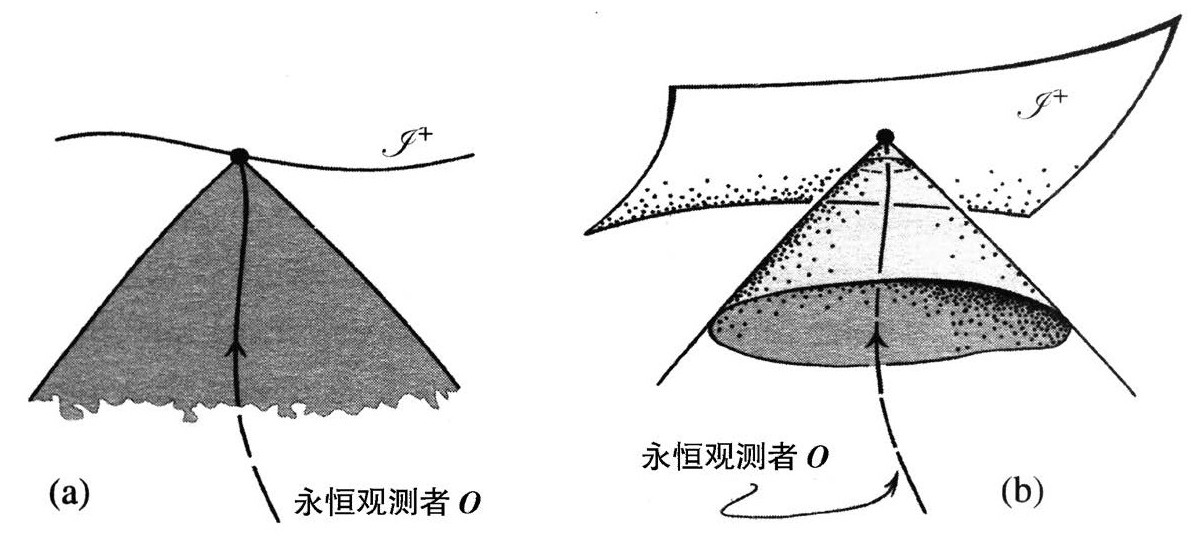
图2.42 Λ>1时出现的宇宙学事件视界的共形草图:(a)2维;(b)3维
当然,多数时空并不具有球对称,严格共形图的描述甚至连合理的近似也做不到。不过,共形草图对澄清思想通常还是有重要意义的。共形草图没有限制严格图的那些确定的法则,为了完整理解这些图形,
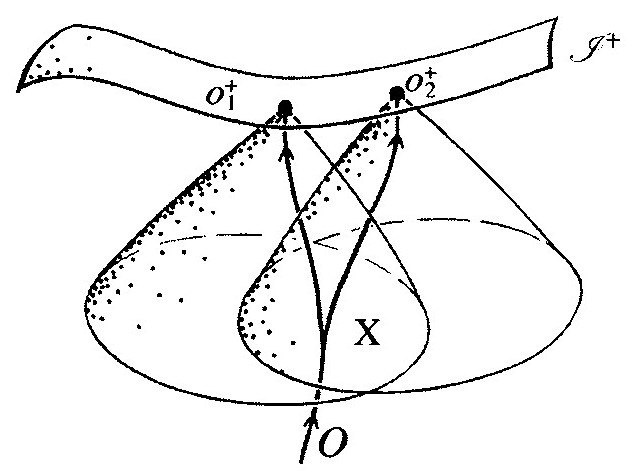
图2.43 永恒观测者O的事件视界代表他所能看到的事件的一个绝对边界,视界本身依赖于O的历史选择。如果在X改变念头,就会导致不同的事件视界
有时我们需要想象它们是在3维或4维中表示的。关键是运用时空共形表示将无限量转化为有限量的两个要点。一方面,将我们在严格共形图中见过的空间和时间的无限区域(由实线边界表示)带进我们的有限认识;另一方面,展开那些不同意义上的无限区域,即在我们严格共形图中以波浪线边界标记的时空奇点。第一点的实现,是用可以光滑地趋于零的共形因子(2.3节中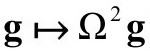 的“Ω”),从而将无限区域“压缩”成有限的东西。第二点的实现是用可以变成无限大的共形因子,通过“拉伸”奇点区而将它转化为有限而光滑的区域。当然,我们不能保证这些过程在任何特殊情形都能真的实现。不过,我们会看到,两个过程在即将面对的问题中起着重要作用,而它们的组合对我在第3部分提出的东西更是至关重要。
的“Ω”),从而将无限区域“压缩”成有限的东西。第二点的实现是用可以变成无限大的共形因子,通过“拉伸”奇点区而将它转化为有限而光滑的区域。当然,我们不能保证这些过程在任何特殊情形都能真的实现。不过,我们会看到,两个过程在即将面对的问题中起着重要作用,而它们的组合对我在第3部分提出的东西更是至关重要。
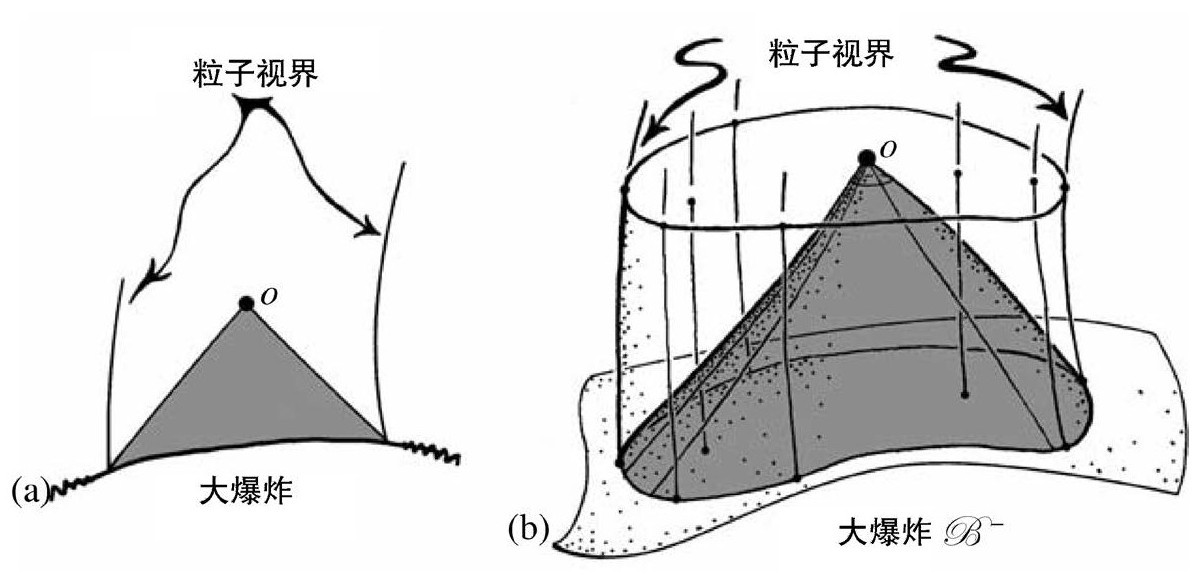
图2.44 粒子视界的共形草图:(a)2维;(b)3维
结束这一节时,我们提出一个具体的和宇宙学视界问题相关的背景,从中可以看到这两个过程特有的启发意义。实际上,在宇宙学背景下,有两个不同的被称为“视界”的概念。[2.48]一个是我们知道的事件视界,另一个是粒子视界。
先考虑宇宙学事件视界。它和黑洞的事件视界有着密切联系,尽管后者具有更“绝对”的特征——因为它不那么依赖于其他观测者的观点。如果一个宇宙学模型,像图2.35的严格共形图所刻画的Λ>0的弗里德曼模型和图2.36(b)的德西特模型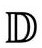 一样,具有类空的未来无限远
一样,具有类空的未来无限远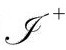 ,那么它就会出现宇宙学视界,但这个概念也适用于不具有对称性的类空
,那么它就会出现宇宙学视界,但这个概念也适用于不具有对称性的类空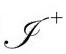 的情形(这是Λ>0的普遍特征)。在图2.42(a)和(b)的概化共形图中,我用终结于
的情形(这是Λ>0的普遍特征)。在图2.42(a)和(b)的概化共形图中,我用终结于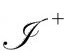 的点o+的世界线l来表示原则上可以被观测者O(假定他是永恒的!)看见的时空区域(2个或3个时空维)。这个观测者的事件视界
的点o+的世界线l来表示原则上可以被观测者O(假定他是永恒的!)看见的时空区域(2个或3个时空维)。这个观测者的事件视界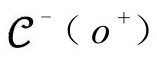 是o+的过去光锥。[2.49]任何发生在
是o+的过去光锥。[2.49]任何发生在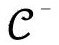 (o+)外的事件将永远不会被O看到。见图2.43。不过我们要注意,事件视界的精确位置强烈依赖于特殊的终点o+。
(o+)外的事件将永远不会被O看到。见图2.43。不过我们要注意,事件视界的精确位置强烈依赖于特殊的终点o+。
另一方面,如果过去边界——通常认为是奇性的而不是无限的——是类空的,就会出现粒子视界。实际上,我们可以从出现奇点的那些严格共形图看到,类空特征是时空奇点的正常性质,这与“强宇宙监督”问题有着密切关系,我将在下一节讨论。现在我们称那个初始奇点边界为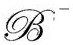 。如果事件o是某个观测者O的时空位置,那么我们可以考虑o的过去光锥
。如果事件o是某个观测者O的时空位置,那么我们可以考虑o的过去光锥 ,看它在哪儿与
,看它在哪儿与 相遇。任何从
相遇。任何从 出发的交界面外的粒子都不可能进入o的观测者能看见的区域,尽管O的世界线可以向未来延伸,能看到越来越多的粒子。我们通常将事件o的实际粒子视界看作一个理想化星系从
出发的交界面外的粒子都不可能进入o的观测者能看见的区域,尽管O的世界线可以向未来延伸,能看到越来越多的粒子。我们通常将事件o的实际粒子视界看作一个理想化星系从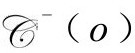 与
与 的交界面出发的世界线所经历的轨迹,如图2.44。
的交界面出发的世界线所经历的轨迹,如图2.44。
2.6 大爆炸怎么特殊了?
现在我们回到这个部分要解决的基本问题,即我们的宇宙何以从如此奇异的大爆炸开始——尤为特别的是它所呈现的非常特殊的方式:从引力方面说,它的熵比它应有的值低得多,而从其他任何方面说,那个熵却接近极大值。然而,在多数现代宇宙学的考虑中,问题似乎越来越糊涂了,这都源于人们的一个普遍观点:宇宙在它出现的极早时期,在紧跟大爆炸后约10-36秒到10-32秒之间的短暂时间里,经历过一场指数式的膨胀——即常说的宇宙的暴胀——使宇宙的线性尺度增大了约1020到1060倍,甚至10100倍。提出这个巨大的膨胀,是为了解释早期宇宙的均匀性(等其他性质),其中所有早期的不规则性都通过膨胀而彻底消解了。不过,似乎很难认同这些讨论解决了我在第一部分关心的基本问题,即大爆炸所表现的极端特殊性,那必须是从一开始就呈现的性质,才会有热力学第二定律。而作为暴胀基础的观点认为,我们现在看到的宇宙的均匀性应该是(暴胀的)物理过程作用于早期演化的结果。在我看来,这是一个根本的误会。
为什么我说它是误会呢?让我们从一般的考虑来考察这个问题。暴胀的基础动力学和其他物理学过程一样,遵从同样的普遍法则,其行为的背后存在时间对称的动力学定律。存在一种被称为“暴胀场”的特殊的物理场,是它决定了暴胀,尽管控制暴胀场的方程的精确性质一般会随暴胀形式的不同而不同。作为暴胀过程的一部分,还会发生某种“相变”,类似于在冰点和熔点发生的固态与液态之间的转变。这种相变可以认为是遵从第二定律的过程,通常伴随着熵的增加。于是,在宇宙动力学中融入暴胀场并不影响我们在第一部分提出的论证。我们仍然需要认识宇宙的异常低熵的初始状态。根据2.2节的讨论,这个低熵根本依赖于引力自由度没有被激发出来——至少不像其他相关自由度那么活跃。
那么,高熵的初始态应该像什么样子呢?在我们必须考虑引力自由度时,认识这一点当然是有帮助的。如果想象坍缩宇宙的时间反演背景,我们可以部分理解这一点。因为这种坍缩,假如服从第二定律的话,应该产生一个真正高熵的奇点状态。应该清楚的是,仅仅对坍缩宇宙的考虑,并不涉及我们实际的宇宙是否像图2.2的Λ=0的封闭弗里德曼模型那样会再坍缩。这个坍缩只是一种假想情形,它当然服从爱因斯坦方程。在一般坍缩的情形,如2.4节考虑的黑洞坍缩,我们相信各种不规则性都会出现,可是当局部的物质区域变得足够致密时,俘获面就可能形成,从而时空奇点也跟着出现。[2.50]不论初始出现什么样的密度不规则性,它都会大大地加强,最终的奇点会从一团凝结的黑洞产生出来。这时,别林斯基、卡拉尼科夫和栗弗席兹的考虑该发挥作用了。假如BKL猜想是对的(见2.4节),那么一定会出现某种极端复杂的奇点结构。
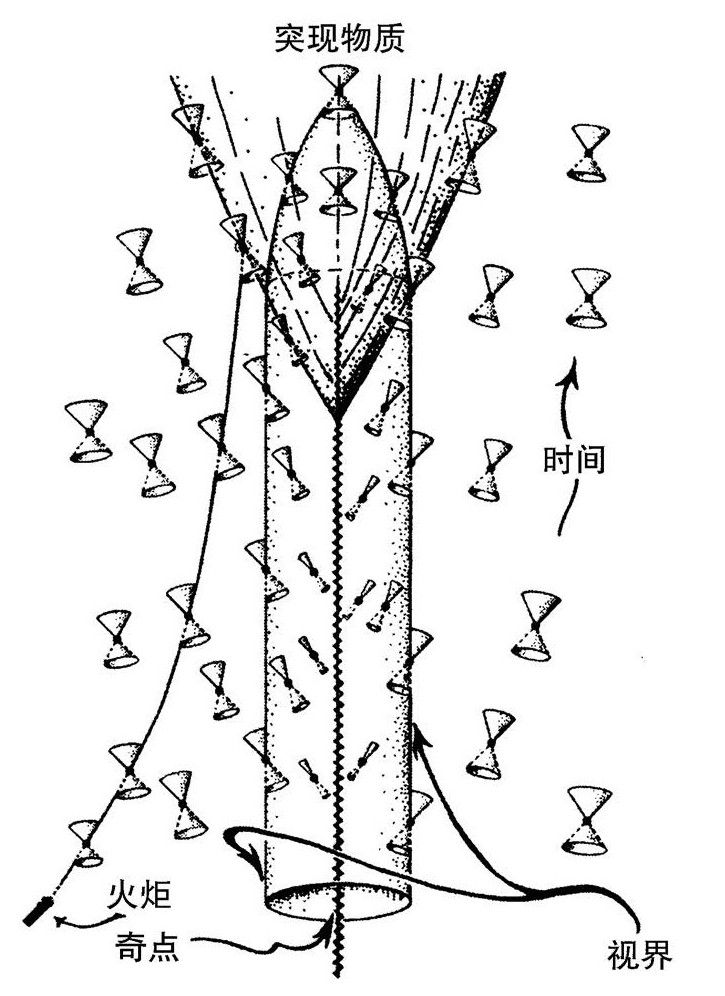
图2.45 假想的“白洞”,是图2.24描绘的那种黑洞的时间反演。这是严重违反第二定律的。光不可能进入视界,所以从左下角的火炬发出的光只有在黑洞爆炸成为普通物质后才能进来
我马上回来谈这个奇点结构问题,不过现在我们考虑暴胀物理的意义。我们只关心宇宙在解耦时(例如)的状态,那时正好产生我们今天看到的CMB辐射(见2.2节)。在我们实际的膨胀宇宙中,当时的物质分布有着极高的均匀性。这显然是一个难题——否则就用不着引入暴胀来解释它了!既然认同有东西要解释,那么我们必须考虑相反的情形,即宇宙那时也许有很强的不规则性。这样,暴胀学家们的主张就等于说,暴胀场的存在使那种不规则性变得不可能了。真是这样的吗?
当然不是,因为我们可以想象解耦时的高度起伏的物质分布状态(不过时间是倒转的),于是这个图像代表了一个非常不规则的正在坍缩的宇宙。[2.51]随着我们想象的宇宙向内坍缩,不规则性将放大,对FLRW对称(2.1节)的偏离也会越来越远。于是,这种状态将远离FLRW的均匀和各向同性,那么暴胀场的暴胀能力也将失去作用,而(反时间的)暴胀也就不可能发生,因为它强烈依赖于一个FLRW背景(至少我们的实际计算结果是这样的)。
于是我们明白了,我们的不规则坍缩模型将坍缩到一个可怕的黑洞成团的状态,生成高度复杂的高熵奇点,很可能像BKL类型,而不大可能是那种似乎在我们的大爆炸中出现过的、像闭合的FLRW形式的高度均匀的低熵奇点。这将是独立发生的,与实际的物理过程中是否存在暴胀场无关。于是,如果再把我们想象的坍缩的块状宇宙的时间反转过来,获得一个膨胀的宇宙,我们会发现它从一个高熵的奇点开始,那个奇点可能是我们实际宇宙的一个初始态,而且是比实际发生过的大爆炸更加可能的初始态(即具有更高的熵)。在我们想象的坍缩的最终阶段凝结在一起的黑洞,当时间反转为膨胀宇宙时,将为我们呈现一幅由多个分岔的白洞组成的初始奇点的图像![2.52]白洞是黑洞的时间反演,我在图2.45中指出了它为我们呈现的这种情形。可这种白洞奇点完全不曾出现,正是这一点凸显了大爆炸的极端特殊性。
从相空间体积看,具有这种性质的初始奇点(多分岔的白洞)比类似于我们大爆炸类型的奇点占据着更大的区域。仅凭暴胀场的可能存在当然不能提供足够的力量来“抹平”那样一堆白洞奇点的不规则性。这一点我们是蛮有信心的,更不用说暴胀场性质的具体考虑了。这只不过是一个方程的问题,要求它能同样地在正反两个时间方向演化,直至达到某个奇点状态。
但是,我们当然还可以把相空间体积的真实大小说得更详细一些,只要我们根据贝肯斯坦—霍金的黑洞熵值公式考虑实际赋予黑洞的熵(也就相当于相空间体积)。对质量为M的非旋转黑洞,熵为
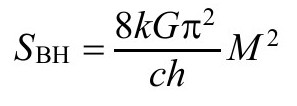
如果黑洞是旋转的,那么熵居于这个数值和它的一半之间,依赖于旋转的量。M2前的因子其实是常数,k, G和h分别为玻尔兹曼、牛顿和普朗克常数,c是光速。实际上,我们可以将熵公式写成更一般的形式:
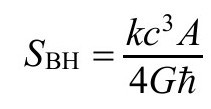
其中A是视界的面积,=h/2π。这个公式适用于旋转或不旋转的黑洞。用3.2节末尾引入的单位,我们有
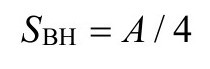
对这个熵,虽然在我看来眼下还不能完全满意地通过黑洞内部状态数来解释,[2.53]但这个熵的数值依然是维护黑洞外量子物理世界的第二定律的基本因素。正如我们在2.2节说的,对当下宇宙熵的最大贡献——还不足总熵的10-10——无疑来自星系中心的巨大黑洞。假如我们今天可观测宇宙(即在我们今天的粒子视界之内)的所有物质的总和终将形成一个黑洞,那么它将达到大约10124的熵,我们可以认为这粗略提供了包含同样质量的坍缩宇宙所能达到的熵的下限。相应的相空间体积大约是
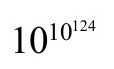
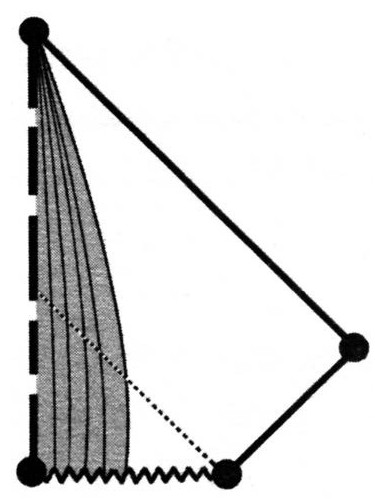
图2.46 图2.45的白洞的严格共形图
(因为1.3节的玻尔兹曼熵公式取了对数),而对同样的物质实体来说,[2.54]实际观测到的对应于解耦时的宇宙状态的相空间区域(即观测的CMB内的区域)具有的体积不超过
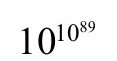
我们处于如此特殊的宇宙,如果纯粹源于偶然,[2.55]则其概率将是一个荒唐至极的小数,大约为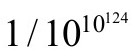 ,而与暴胀无关。这类数字正需要一种完全不同类型的理论解释!
,而与暴胀无关。这类数字正需要一种完全不同类型的理论解释!
然而,还有一个更深层的问题,可以认为在这儿有着重要意义。那个问题是,具有如此复杂的白洞型结构的初始奇点是否能合理地当作一个“瞬时事件”?这个问题大致等于问,当我们把如此奇点看成时空的某种过去“共形边界”时,是否可以认为它是“类空的”?然后,我们可以认为这样的类空初始奇点代表了某个宇宙时间坐标的零点,也就是那个高度不规则的大爆炸发生的“时刻”。
实际上,奥本海默—斯尼德坍缩的时间反演真有一个类空的初始奇点,这可以清楚地从图2.46(图2.38的时间反演)的严格共形图看出来。而且,这种类空特征正是一般BKL奇点所具有的基本性质。更一般地说,一般性奇点(允许它们在某些地方可以是零)的类空性是基于强宇宙监督的预期结果,[2.56]尽管宇宙监督还只是未经证实的关于爱因斯坦方程解的猜想(2.4节说过了)——它告诉我们“裸奇点”不可能出现在一般的宇宙坍缩中,坍缩产生的奇点总是逃避直接的观测,例如躲在黑洞的事件视界背后。强宇宙监督告诉我们,这些奇点至少在一般情形应该是类空的。遵照这个预言,我想完全有理由认为那种白洞主导的初始奇点确实是一个瞬时事件。
一个重要的问题来了:凭什么用几何准则来区分代表大爆炸低熵的“光滑”奇点和从白洞的时间反演坍缩产生的更一般的高熵奇点?我们需要明确界定“引力自由度没有被激发出来”的意思。但是,为了这一点,我们需要认定是哪个数学量确实度量了“引力自由度”。
引力场的一个很好的类比是电磁场,它们在很多重要方面都很相似,尽管也存在一些重要区别。在相对论物理中,电磁场用张量F来描述,叫麦克斯韦场张量——用苏格兰科学家麦克斯韦(James Clerk Maxwell)的名字命名,他在1861年发现了电磁场满足的方程,并证明这些方程解释了光的传播。可以回想一下,我们在2.3节遇到过另一个张量,即度规张量g。张量是广义相对论的基本工具,是几何或物理实体的数学描述,而且其形式不受我们在2.3节考虑的“橡皮几何”的变形(微分同胚)的影响。张量F取决于每一点的6个独立数(3个电场分量,3个磁场分量)。度规张量g在每一点有10个独立分量。在标准张量记号中,通常用带两个下标的符号gab(或类似的符号)记度规的分量集合,它有对称性gab=gba。对麦克斯韦张量F,分量集记为Fab(具有反对称性Fab=-Fba)。每个这样的张量都有一个型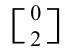 ,意思是只有两个下标。但也会出现带上标的张量,
,意思是只有两个下标。但也会出现带上标的张量,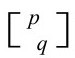 型张量就描述有p个上标和q个下标的分量集。张量有一个叫缩并(或内积)的代数运算,它允许我们将一个上标与一个下标联系起来(以化学键的方式),从而在最后的表达式里消去那两个指标——但我不想在这儿讲张量的代数运算。
型张量就描述有p个上标和q个下标的分量集。张量有一个叫缩并(或内积)的代数运算,它允许我们将一个上标与一个下标联系起来(以化学键的方式),从而在最后的表达式里消去那两个指标——但我不想在这儿讲张量的代数运算。
电磁场的自由度其实就是用麦克斯韦张量F度量的,但在麦克斯韦理论中,电磁场还有一个源,叫电荷—电流矢量J。这可以视为一个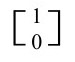 张量,每一点的4个分量描述电荷密度的1个分量和电流的3个分量。在静态情形,电荷密度起着电场的源的作用,而电流密度是磁场的源。可是在非静态情形,问题就复杂了。
张量,每一点的4个分量描述电荷密度的1个分量和电流的3个分量。在静态情形,电荷密度起着电场的源的作用,而电流密度是磁场的源。可是在非静态情形,问题就复杂了。
我们现在寻求引力场情形下,由爱因斯坦广义相对论描述的类似的F和J。在这个广义相对论中,有一个时空曲率(只要知道度规g在时空里如何变化,就可以计算),由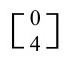 张量R描述,叫黎曼(-克里斯多菲尔(Christoffel))张量,它有较为复杂的对称性,使R在每一点有20个独立分量。这些分量可以分解为两个部分:一个构成
张量R描述,叫黎曼(-克里斯多菲尔(Christoffel))张量,它有较为复杂的对称性,使R在每一点有20个独立分量。这些分量可以分解为两个部分:一个构成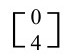 张量C,10个独立分量,叫外尔(Weyl)共形张量,另一个构成对称
张量C,10个独立分量,叫外尔(Weyl)共形张量,另一个构成对称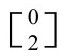 张量E,也有10个独立分量,叫爱因斯坦张量(等价于一个略微不同的
张量E,也有10个独立分量,叫爱因斯坦张量(等价于一个略微不同的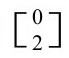 张量,叫里奇(Ricci)张量)[2.57]。根据爱因斯坦场方程,为引力场提供源的正是E,它通常表达[2.58]为
张量,叫里奇(Ricci)张量)[2.57]。根据爱因斯坦场方程,为引力场提供源的正是E,它通常表达[2.58]为
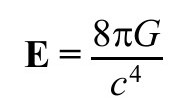
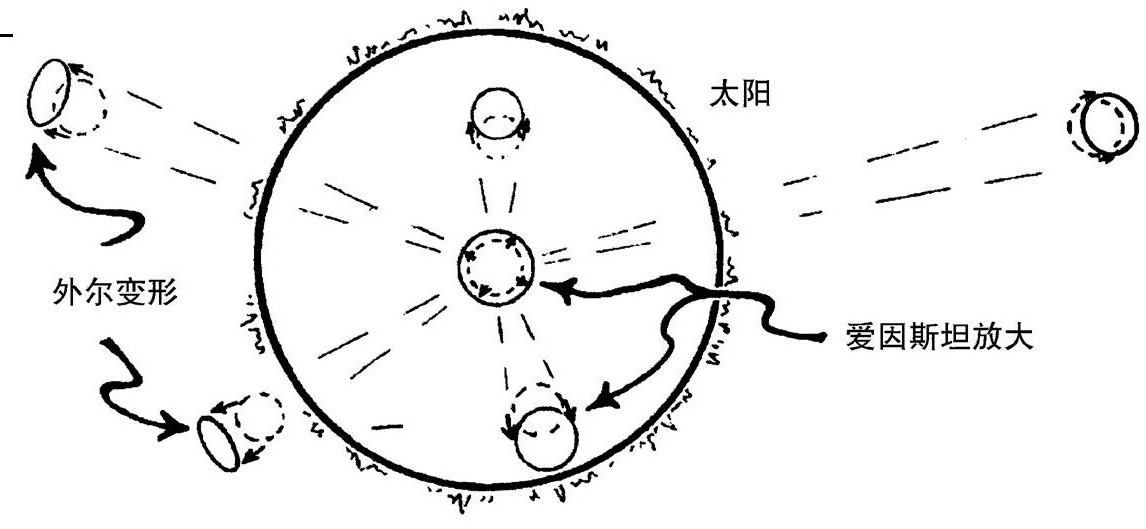
图2.47 引力体(这里是太阳)周围外尓曲率的存在,可以从它对背景场的扭曲(非共形的)效应看出来
或用3.2节的普朗克单位,简化为

其中Λ为宇宙学常数,能量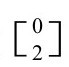 张量T代表质量-能量密度和其他相对论要求的相关量。换句话说,E(或能量张量T)就是J的引力类比。那么,外尔张量C就是麦克斯韦F的引力类比。
张量T代表质量-能量密度和其他相对论要求的相关量。换句话说,E(或能量张量T)就是J的引力类比。那么,外尔张量C就是麦克斯韦F的引力类比。
我们可以问C和E有什么可以直接观测的效应,正如铁屑的排列或罗盘的指针显现磁场,木髓球的效应显现电场,等等。实际上,在几乎相同的意义上,我们真可以看到E的效应,特别是C的效应,因为这些张量对光线有着直接而且可以区分的效应——从这方面说,E和T是完全等价的,因为Λg对光线没有影响。我们可以明确地说,第一个支持广义相对论的清晰证据正是那样的直接观测——那是在1919年日食期间,爱丁顿爵士远征普林西比岛去观测恒星位置因为太阳的引力场而产生的显著偏离。

图2.48 引力透镜:(a)星系团Abell1689;(b)星系团Abell2218
大致说来,E的作用像放大镜,而C像纯粹的散光透镜。如果想象光线经过或穿过大质量物体(如太阳)时会如何受影响,就能很好体会这些效应。当然,普通光线不会真的穿过太阳内部(在月食的时候,也不可能穿过暗淡的月亮),所以我们在这种情形下不会直接看到那些特殊的光线。但可以想象,假如我们真的能透过太阳看到那一片星空,那片视野将因为E的存在而略有放大,那儿也是太阳的引力物质存在的地方。E的纯效应就是放大背后的视野,而没有变形。[2.59]然而,对太阳圆盘外的一片遥远星空的变形图像(这也是实际看到的),我们会发现,越向外看,向外的位移就越来越小,这就形成遥远星场的散光扭曲。图2.47说明了这些效应。由于太阳边缘外的视域变形,遥远星空的小圆模式看起来就像椭圆,而椭圆性(椭率)正是光线所截取的那部分外尔曲率C的度量。
实际上,最初由爱因斯坦预言的这种引力透镜效应,已经成为现代天文学和宇宙学的极端重要的工具,因为它提供了一种观测物质分布的方法。如果没有它,可能有些东西就完全不可能看见。在多数情形,遥远的背景视域都包含大量遥远星系。我们的目标是确定那个背景视域里是否出现显著的椭率,然后我们用它来估计产生这种椭圆模式的引力场的物质分布。然而,问题是星系本身就是椭圆形的,所以我们通常不可能分辨单个的星系图像是否发生了形变。不过,因为有大量远视域的星系,统计就有意义了。我们常常可以用统计的方法得到一些非常令人满意的物质分布估计。有时,甚至可以用肉眼来判断。图2.48提供了一些重要例子,其中椭圆模式使透镜源的存在表现得尤为显著。这个技术的一个重要应用是画出暗物质分布(见2.1节),因为用其他方法是看不见它们的。[2.60]
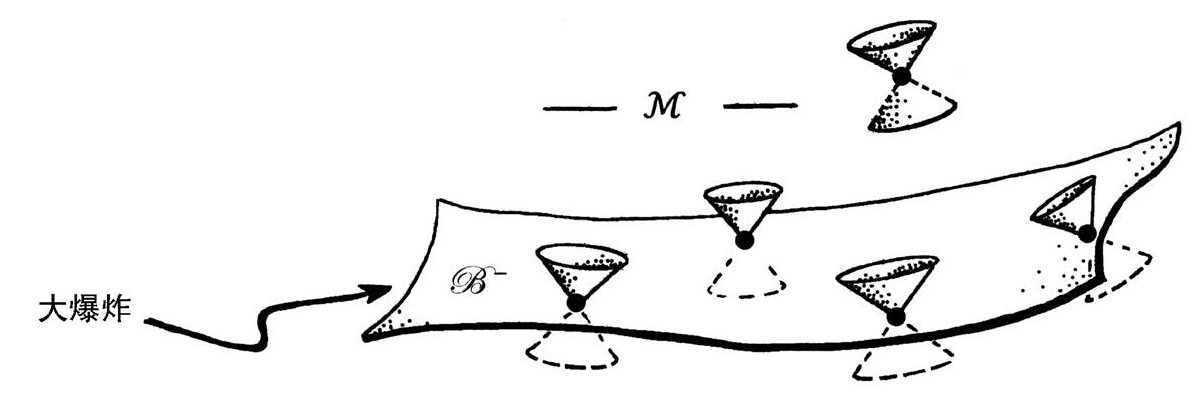
图2.49 托德的“外尔曲率假定”形式的共形草图,断言大爆炸为时空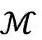 提供了一个光滑边界
提供了一个光滑边界
C在光线方向产生椭率的事实,意味着它可以充当描述共形曲率的量。2.3节最后指出,时空的共形结构实际上就是它的零锥结构。于是,时空的共形曲率(即C)度量了零锥结构对闵氏空间 的偏离。我们看到,这种偏离的本性在于它使光束产生椭率。
的偏离。我们看到,这种偏离的本性在于它使光束产生椭率。
现在我们来看为了刻画大爆炸的特殊性需要什么条件。大概说,我们需要证明引力自由度在大爆炸时尚未被激发,这等于说“外尔曲率C在那儿消失了”。多年来,我一直假定诸如“C=0”的条件对初始型奇点成立,这与出现在黑洞的“终结型”奇点的情形正好相反——对黑洞来说,C可能变成无限大,例如在奥本海默-斯尼德坍缩趋于奇点德情形;也可能非常剧烈地发散,例如在BKL奇点情形。[2.61]一般来说,C在初始奇点为零的条件——我称为外尔曲率假设(WCH)——看起来很恰当,但也有些尴尬,因为它实际上可以有很多不同的表述方式。大概来说,麻烦在于C是张量,对这种量在时间奇点的行为,很难做出明晰的数学判断,因为不论在什么坐标系,张量概念本身在奇点处都会失去意义。
幸运的是,我的牛津同事托德(Paul Tod)曾详尽研究过一个不同的但在数学上更令人满意的构建WCH的方法。大意是说,在一定程度上,存在一个大爆炸3维曲面,当M为共形流形时,曲面表现为时空M的光滑过去边界,正如图2.34和2.35的严格共形图展示的完全对称FLRW模型的情形;不过这儿没有假定那些特殊模型的FLRW对称性,见图2.49。托德建议至少约束C在大爆炸是有限的(因为在的共形结构被假定为光滑的),而不是狂野地发散的,这个陈述大概能很好地满足我们的要求。
为了使这个条件在数学上更清晰,可以方便地假定时空在这种形式下能像共形流形一样光滑延拓到超曲面之前一点儿。延拓到大爆炸135之前?当然不是:大爆炸被认为代表万物的起点,所以不会有“之前”。别怕——这只是一个数学游戏。延拓没有任何物理意义!
或者也许……
