译后记　宇宙是怎么轮回的？

玻尔喜欢用“有趣的疯狂”来说一个新理论。1958年，他告诉泡利说：“我们一致认为你的理论很疯狂；我们的分歧在于，它是不是疯得够狂而可能是对的。”读者读过本书，会不会认为它疯狂呢？它是不是疯得够狂，也许是对的呢？

彭老师自己感觉它很疯狂，在尾声中还借小朋友的话总结说，“那是我听过的最疯狂的思想！”什么思想呢？“共形循环宇宙学”（CCC）——从大爆炸开始的宇宙终结于一个加速膨胀的时空，形成一个世代；每个世代的终结是下一个世代的大爆炸的开始……换句话说，CCC描绘了一个无限的宇宙循环。我们这个从大爆炸开始的膨胀的宇宙，是无限多个相似的宇宙世代中的一个。我们的大爆炸其实是前一个时代的遥远未来的延续。用数学的语言说：前一个世代的共形无限远（一个共形的4维流形）光滑延拓为下一个世代的大爆炸。因为无质量场的爱因斯坦方程是共形不变的，那个“垂死的”宇宙中的观测者（无质量粒子）“感觉”不到大爆炸的奇点，可以悠悠然从那个宇宙走进新的宇宙，重新捡起一个新的共形因子，进入演化的“宇宙新世代”。

借彭老师自己的话说（3.1节）：怎么能把遥远的未来同大爆炸式的起点等同起来呢？况且，未来的辐射冷却到零，密度稀薄到零；而在大爆炸起点，辐射有无限的温度和密度……况且，根据热力学第二定律，宇宙总是向着熵增大的方向演化，既然总是增大，如何能回到原点形成“循环”呢？

本书系统考察了那些问题，但细节太多，也许读者不能“一目了然”，所以我根据自己的理解写一个提纲，简单“回顾”CCC的要点，也顺便补充一些书以外的东西，希望有助于读者领会彭老师的思想。

1.CCC的轮廓

CCC对那两个问题的回答，也是它的两个要点：第一，宇宙的初态是低熵的，而终态是高熵的，其演化满足热力学第二定律；第二，一个世代的初态与前一个世代的终态通过共形几何实现光滑的过渡。

我们的未来最终是一个大黑洞。假定把所有物质（大约10⁸⁰个重子，不考虑暗物质）都扔进黑洞，那么根据霍金的熵公式，可得熵为10¹²³，而相空间体积是10后面跟那么多零。

在宇宙之初，引力自由度尚未激活，相空间很小，所以处于低熵态。当那些自由度激发起来时，引力作用就开始起主导作用，进入多彩的演化时代，形成各种尺度的宇宙结构，也包括生命和我们。

初始奇点（大爆炸）与终结奇点（黑洞）的特征，恰好可以用Weyl曲率张量来描述，因而它自然成为刻画引力熵的物理量。Weyl曲率是共形不变的，在大爆炸的共形扩张会将无限大的密度和温度降到有限的数值，而无限远的共形收缩会将零密度和温度提高到有限的数值。于是，两者在界面光滑地过渡，宇宙也就从旧世代演进到新世代。这就是所谓的“共形循环宇宙论”（CCC）。

2.CCC的逻辑

2.1）Weyl曲率是共形的

从以上轮廓可见，Weyl曲率是CCC的数学核心。实际上，Weyl曲率的故事大概可以从30多年前说起。1979年，剑桥大学出版社出版了一本由霍金等人编辑的纪念爱因斯坦的文集《广义相对论：爱因斯坦百年概观》（General relativity：An Einstein Centenary Survey，eds.S W Hawking and W Israel, Cambridge University Press，1979），彭老师写了一篇50多页的《奇点与时间不对称》（“Singularities and time-asymmetry”），将第二定律的起源追溯到宇宙的边界条件，也就是奇点（初始的或终结的）。他指出，从时空曲率说，早期宇宙没有出现物质的聚集，对应于没有Weyl曲率（因为没有聚集意味着空间各向同性，也就意味着没有引力主导的零方向）……这个几何约束相当于说，Weyl曲率在任何初始奇点为零。然后，随着引力聚集的发生，其区域的Weyl曲率也不断增大，最后引力坍缩形成黑洞时，曲率在奇点变成无限大。这就是Weyl曲率猜想（WCH）。WCH有不同的形式，“强式”的说初始Weyl曲率为零，“弱式”的说初始时物质（即Ricci张量）起主导作用，而终结时相反。WCH是与奇点和宇宙“命运”联系在一起的，如“各项同性（isotropic）奇点”、“宁静（quiescent）宇宙学”等，都与它有关。

Weyl曲率是什么呢？我们知道，广义相对论是用时空的曲率（Riemann曲率）来描述引力场，爱因斯坦的场方程的实质就是时空曲率张量等于物质的能量动量张量。Weyl曲率就是Riemann曲率的“无迹”部分。（用矩阵来表示，“无迹”的意思就是对角线元素之和等于零。）因为场方程是缩并（即对角元素求和）之后的结果，所以没有Weyl张量。但Weyl曲率在无引力源的“虚空”仍然会有“潮汐”效应，而且在非完全各向同性的条件下不为零。

也可以通过电磁场的类比来说明Weyl张量。描述电磁系统（Maxwell方程）有两个张量：一个是电磁场的Maxwell张量，一个是场源（电荷或电流）。Riemann张量也是两部分，一个是Ricci曲率，描述引力源（相当于电磁场的电荷—电流源），引力效应表现为物质对时空的扭曲（如经过引力源附近的光线偏折，行星轨道的进动），另一个就是Weyl曲率，度量无源引力场的时空曲率（类似无源的Maxwell张量）。正如Maxwell张量可以分解为电（E）、磁（B）两个部分（具体的分解依赖于观测者的状态），Weyl曲率也能分解为电、磁两个部分，这个特点对CCC的观测证据有很大影响（附录B最后用了这个划分）。Weyl张量的一个好品质是“共形不变”，即不随尺度大小变化，只与形状有关（其实，所谓“共形”，就是初等几何里所说的“相似”或复函数论里常说的“保角”）。关于Weyl曲率，彭老师在《通向实在之路》（第28章）里有更详细的解说，可以参阅。

用Weyl张量来刻画宇宙初始和终结的状态，是因为两个态都不需要考虑物质源，只有纯粹的时空几何效应。WCH说，Weyl曲率初时为零终结时最大，这恰好与熵的变化“平行”。所以直观说来，Weyl曲率刻画了引力的熵。但WCH与第二定律的熵增只是形式上的呼应，并不是严格的数学和物理学的熵定义。一个自然的想法是，用Weyl曲率张量（或者结合Ricci张量）来构造某个不变量（例如，其缩并就是一个标量），要求其行为满足熵的特征（如非负的、连续的、单调递增的，等等），那就有可能作为引力熵的定义。遗憾的是，虽然有过一些尝试，但还没有满意的结果。

2.2）大爆炸是低熵的

大爆炸是各向同性的奇点——将各向同性的微波背景辐射（CMB）倒推回去，就可以想象它是各向同性的。CMB不仅在大尺度上均匀且各向同性，而且满足Planck的黑体辐射曲线。这意味着“我们看到的东西来自一个肯定是热平衡的状态”（2.2节）。“热平衡”意味着它有最大的相空间，因而有最大的熵——这就引出一个问题：根据第二定律，初始态应该是低熵态，而我们看到的却是高熵的。另一方面，如果根据CMB的数据估计大爆炸的相空间，却可以发现它确实是很小的。彭老师的计算表明，初始的相空间与宇宙最后的黑洞（根据所有物质即重子数计算）的相空间相比，只有10的10¹²⁴分之一！

问题在于我们忽略了引力。如彭老师在2.2节里的例子（图2.8）：在不考虑引力时，自然朝着均匀态演化，所以均匀（热平衡）代表高熵态；但在引力出现时，自然朝着聚集的方向演化，均匀却是初始的低熵态。宇宙初始的均匀态，是引力自由度被约束的态，所以熵很低。（顺便说一句，引力作用自然消除了过去所谓的宇宙“热寂”问题。）

Lee Smolin有一个很好的比喻说：我们有两个温度，一个是火热的物质和辐射的温度，一个是冰冷的引力的温度。换句话说，普通物质是高温向低温演化，而引力作用的结果是向高温演化。（回想一下，熵最初的定义就是从热过程的卡诺循环引出来的。）彭老师通过太阳解释了引力熵的特点：“太阳对我们并不仅是简单地提供能量，而是提供低熵形式的能量，这样我们（通过绿色植物）才能降低我们的熵，之所以如此，是因为太阳是黑暗天空里的一个热点。”（2.2节）太阳提供低熵，等于说它源源不断地输出负熵，那么它自己的熵会越来越大。这种“组织性”的特征，也可以从生命的演化来认识。

大爆炸奇点的特殊（各向同性且低熵），就在于它的引力自由度还没被激发出来，在数学形式上就表现为（也许因为量子引力的原因）Weyl曲率张量为零（或远小于Ricci曲率）。如果重新标度度规，那么Weyl曲率就等于正常状态下的曲率。书中多次提及的FLWR宇宙，就是Weyl曲率等于零的例子，不过那个宇宙模型对称性太高，Weyl曲率是恒等于零的。WCH的意义在于，它对很多不那么对称的奇点也是成立的。这一点很有现实意义，毕竟真实的宇宙并不是理想对称和各向同性的。

2.3）第二定律是“重生”的

从奇点性质看，宇宙开始的状态（大爆炸）与终结的状态（黑洞）是不同的；但在其他诸多方面，二者又是相似的——不是“几乎相同的相似”，而是几何意义的相似（也就是“共形”），即它们看起来只有尺度的差别。

最突出的相似是两个时期的所有物质都是零质量（无静止质量）的粒子。严格说来，这是一个假定的事实，涉及很多未解的难题，如粒子衰变、静止质量、黑洞蒸发、信息丢失等等（见3.2节）。如果不管那些细节，那么物质演化就仿佛粒子与黑洞的生灭游戏——这也是近年来的一个新认识：基本粒子与黑洞没有根本的不同，黑洞是基本粒子的自然延伸。随着宇宙的膨胀（时间尺度为10¹⁰⁰年），粒子会逐渐失去质量——要么通过与反粒子伙伴湮灭，要么自我衰变——留下无质量的粒子和大质量的黑洞（它们是星系或大恒星留下的）。相应地，温度越来越低，当它低于黑洞温度时，黑洞就开始蒸发，产生无质量的粒子。最后，整个宇宙的粒子都成了无质量的，一切信息都将丢失。因为粒子没有质量，所以不但没有空间的度量工具，时间也将失去度量（借彭老师的话说，我们不能用无质量粒子来做时钟），甚至连共形因子也将被“遗忘”。于是，最后的宇宙看起来就跟大爆炸之前的那个宇宙一样。彭老师将它解释为下一个宇宙的前大爆炸时期……（牛津大学的Barrow早在1978年就根据熵增原理提出，初始的宇宙应该是各向同性的“宁静”的，而不是Misner说的“混沌”的。那个宁静的状态，正是CCC需要的初始态。）

因为整体的尺度变化不会影响熵的度量，那么，热力学第二定律从哪儿来呢？当然要从前面说过的两个奇点的不同来考虑了。具体说来，黑洞最终会在弱弱的一声“砰响”中消失，黑洞里的信息也跟着消失。在奇点的“信息丢失”是什么意思呢？更准确的说法是自由度的丢失。自由度丢失了，相空间的某些参数就消失了，那么相空间就变得比原来小，宇宙重新回到一个低熵的状态，这样就满足第二定律的要求。

黑洞信息是一个老问题。霍金在1975年8月的一篇文章（“可预言性在引力坍缩下的崩溃”）里提出，系统状态的部分信息丢失在黑洞里了。所以，黑洞蒸发后的最终状态不是一个纯量子态。信息丢失显然违背了量子力学的基本法则（也就是彭老师说的幺正演化或“U过程”）。举例来说，假如我们点燃两卷百科全书，它们的火苗和灰烬是不同的，因而在原则上有可能从火苗和灰烬恢复各自的内容。于是，1997年2月，Preskill向霍金和他的朋友Thorne提出了挑战，他认为：“当初始的纯量子态经过引力坍缩形成黑洞时，黑洞蒸发的最终状态将仍然是一个纯量子态。”

2004年7月，霍金在都柏林第17届国际广义相对论与引力论会议（GR17）上报告说，他解决了“黑洞的信息疑难”。他考虑了两类经典时空，有黑洞的（非平凡拓扑）和没有黑洞的（平凡拓扑）。然后，在这两类空间上进行半经典近似的路径积分。在没有黑洞的空间积分，没有信息丢失；而在有黑洞的空间积分，结果是“零”，信息丢了。

在彭老师看来，幺正（U）演化终究是要破坏的。在一个世代的遥远未来，所有黑洞都消失了，宇宙整体的相空间会大大地收缩，熵要重新“清零”。下一个世代的大爆炸将被严格约束——例如满足Weyl曲率猜想，这就为新世代的引力作用提供了强大的潜能。

但“这是一个微妙的问题，相空间体积的减小还存在很多具体的一致性问题需要解决，才能满足CCC的要求。”彭老师最后猜想，“我们可以估计最大黑洞可能达到的贝肯斯坦—霍金熵（只要它不在霍金辐射中丢失），并且将这个总熵作为可能相空间为开启下一个世代所需要的减小量。显然，为了明确CCC在这个方面是否可行，我们还有很多问题需要更详细的研究。”（3.4节）

2.4）初始与终结是共形的

前面说了，宇宙的初始态与终结态是相似的，而大爆炸奇点与黑洞奇点却是不同的。但一个循环的宇宙需要首尾两点的自然连接，靠什么来实现呢？共形几何。

一个是“各向同性过去奇点”，一个是“各向异性未来奇点”。前者的特征是Weyl曲率为零，Ricci曲率为无限大；后者则正好相反，Ricci为零而Weyl无限大。宇宙演化的过程不但是熵无限增大的过程，也是Weyl从零到无穷大的过程，这体现了Weyl张量与熵的直观联系。（关于初始奇点与终结奇点，彭老师在《皇帝新脑》里就讨论过；关于Weyl曲率假设，彭老师与霍金也有过争论，见《时空的本性》。那两本书的中译本都在“第一推动丛书”中，感兴趣的读者可以找来复习一下。）

那么，我们未来的高熵状态又如何能成为下一个世代的大爆炸（低熵态）呢？彭老师说：“在大爆炸的共形‘扩张’会将无限大的密度和温度降到有限的数值，而无限远处的共形‘收缩’会将零密度和温度提高到有限的数值。这正是令两者重叠的重新标度过程……”（3.1节）

牛津的Paul Tod为实现这个自然过程提供了数学依据。他证明，通过用一个随时间变化的函数（共形因子）来重新标度时空，初始的各向同性奇点是可以清除的。在共形的标度变换下（即与时空距离无关），我们其实感觉不到那个初始状态的时空曲面是什么，因而可以将它移到遥远的未来。彭老师通过一个“中间度规”来连接过去世代的度规（通过标度因子Ω）和我们世代的度规（通过标度因子ω）。向界面趋近时，Ω趋于无限而ω趋于零，两个因子“互为倒数”。有趣的是，那个共形因子ω所代表的“幽灵场”（phantom field），可以解释为新生的暗物质的原初形式，并担起初始引力场的自由度。

Ω趋于无限是与前世的暴胀相联系的，它使Weyl曲率在界面为零。但是，曲率在界面的法向导数不为零，这样就可以将“前世”的信息传给“后世”——导数的磁部分决定3维界面的共形曲率，而电部分则度量新生暗物质（由Ω描述）的非均匀性，那个非均匀性是受了前世引力波的轻轻的“冲击”（彭老师用的词儿是kick）。（附录A-B11给出了相关的数学方程。）

那个给暗物质带来的冲击，将穿过界面到达我们世代的最后散射曲面（也就是开始产生微波背景辐射的曲面），在CMB中留下痕迹。什么痕迹呢？

3.CCC的证据

CCC预言，“前一个世代的每一次黑洞相遇（即两个球面相交），都会在CMB天空留下一个圆圈，它对整个天空的背景平均CMB温度有着或正或负的贡献。”（3.6节）具体说来，过去的星系团里有很多超大质量的黑洞，它们的碰撞产生引力波；不同时代不同位置的碰撞源会产生不同的引力波。引力波在穿过世代之交的界面时，会表现为一种推力，将它遇到的物质向外推，犹如雨点落进水池激起向外扩散的波纹一样——当它们达到我们世代的最后散射曲面时，就在CMB的图景中留下无数大大小小的相交的“波纹”圆圈。

每个圆圈周围的温度是均匀的，但与其他圆圈相交的点例外。任意选择一个点，我们考察以它为中心的不同角半径的圆环的温度变化（方差）。假如圆环恰好包含一个引力波的圆圈，则那个圈将为圆环贡献一个相对较强的均匀温度；假如其他经过圆环的点的效应只是简单的叠加而已，那么不论是否存在那个均匀的圆圈，温度的方差都不会改变（因为那个圆圈只是起着背景值的作用）。

而CCC预言的却是，那些点的效应是不能简单叠加的。在前一个世代，甚至直到本世代的大爆炸之后，引力波的非线性效应都可以忽略，仍然可以线性叠加。但是，当宇宙温度降到大约Higgs温度（也就是Higgs机制发生作用的临界温度）以下时，共形场代表的暗物质开始获得静止质量和黏性，会呈现流体运动，于是不同点相交的结果是运动的“平均”而非温度的“叠加”。正是这个非线性效应，使最后看到的圆环都是低方差的。（这是一个简单的统计结果：每个局部平均之后再计算整体的方差，将比根据原来整体计算的方差小。）在圆环恰好与某个圈重合时，那个效应会更加显著，也就是我们很可能在CMB中看到的痕迹。

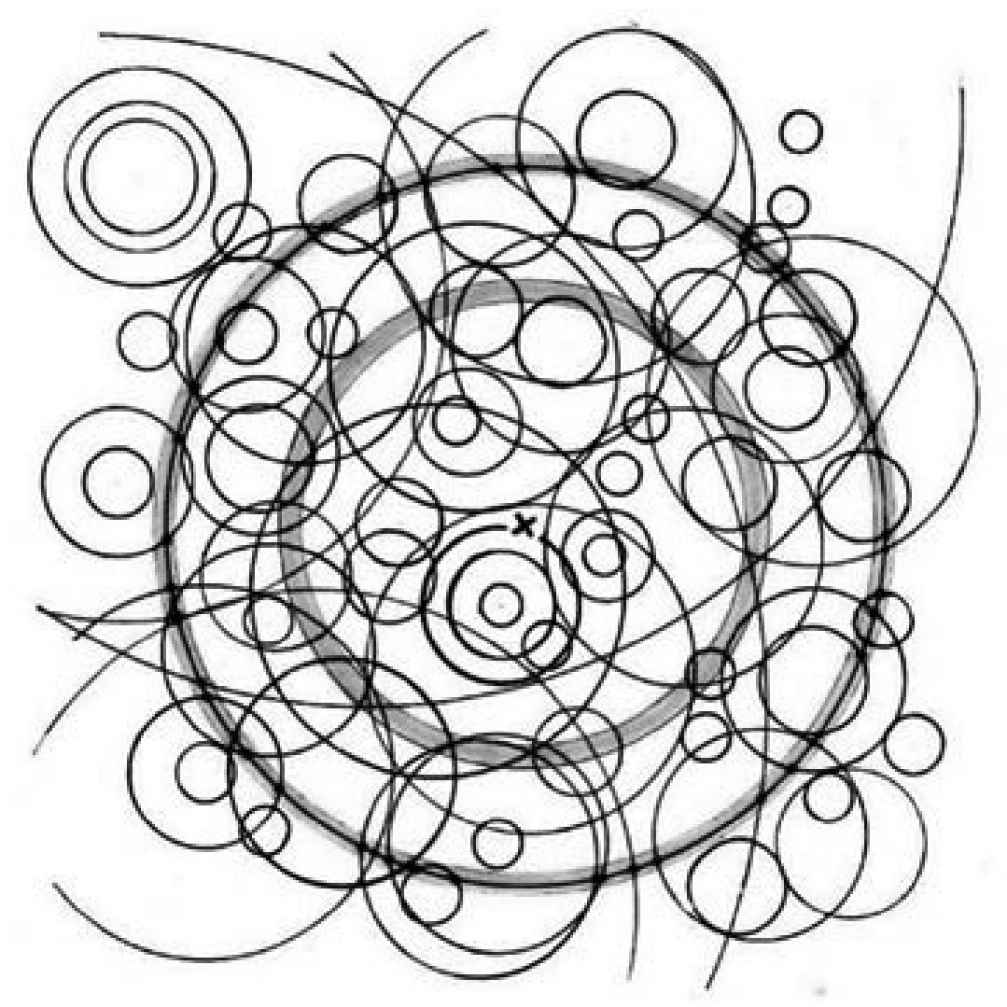
以X为中心寻找圆环（引自arXiv：1302.5162）

果然，近两年来，彭老师从威尔金森微波各向异性探测器（WMAP）的数据发现，CMB确实存在着具有低方差温度的同心圆环结构。

那些圆环是用统计学的方法（如随机模拟CMB数据）计算的，与理论没有关系，CCC只是它们的一种解释——当然，也可以说CCC“预言”了它们的存在（正如超弦理论预言了引力的存在一样）。既然能用随机模拟的数据产生那些圆环，确实就有人指出它们就是纯粹的随机结果；他们还批评彭老师和他的伙伴们混淆了随机与关联的概念——即使他们看到了CMB的圆环，那也只是一种统计关联的表现，本质还是随机的。

在CMB中看到的同心圆环结构（引自arXiv：1011.3706）

彭老师相信他看的圈，不仅因为它们为CCC的概念（也许还说不上严密的计算）提供了现象的根据，还因为他相信CMB不是“那么”随机的。与他一起计算圈结构的合作者Vahe Gurzadyan曾用一种概率论的方法（Kolmogorov方法）发现CMB的随机程度只有20%，那么它存在动力学结构的可能性就很大了。

在这场争论中，随机派有着天然的优势，因为他们不需要解释那些圆圈；而彭老师为了确立CCC，不仅需要确证那些圆圈不是随机的，还需要面对CCC涉及的一系列问题，很多还是物理学的根本问题——如果一个假说能与基本的科学问题发生联系，它就是有意义的。

4.CCC的意义

CCC令人感兴趣的当然不是宇宙的“循环”（循环宇宙已经有90年的历史了），更不是那些圆圈，而是它对第二定律的新解和它简单的逻辑结构（即通过Weyl曲率来解释一系列问题）。正如彭老师自己说的（3.3节），“假如我们坚信前大爆炸相的行为应该遵从第二定律，而且引力自由度开始完全激活，那么必然会发生某种不同于直接反弹的事情，不论经典的还是量子的。我本人解决这个难题的尝试，是我提出CCC这个看起来多少有些奇异的观点的主要原因。”这个主题贯穿了全书，读者可以从细细的品读中去感觉他的精神。

当然，CCC纲领还对宇宙学的很多有趣的问题提出了新的解释，如关于奇点、暗物质、静止质量、宇宙暴胀等。特别重要的一点是，它否定了暴胀论——这是标准大爆炸/暴胀宇宙学的基本组成，我们多说几句。

暴胀模型是为了解释大爆炸留下的视界问题（即因果区域分离的问题）和平直性问题（大尺度时空接近欧氏几何）而提出来的。它假定宇宙在大爆炸之后的一个非常短的时间间隔内（大约在10^-36到10^-32秒之间）经历了一场指数式的膨胀，线性尺度增大10³⁰或10⁶⁰（甚至10¹⁰⁰）倍。暴胀依赖于一个人工色彩很浓的暴胀子的势函数。最近有人怀疑，新发现的Higgs场的特征似乎不利于暴胀的发生。

彭老师对暴胀一贯不感兴趣（2.1节）。他认为第二定律应该从大爆炸一开始就发生作用，宇宙初始的平直性应该是“先天的”，而不应该是暴胀作用的结果。所以，CCC的暴胀相（阶段）发生在的大爆炸之前（前一个世代的遥远未来）（2.6节），这就使得我们的世代从一开始就处于平直的低熵态。CCC里的“前世”暴胀与传统暴胀的区别还在于，传统暴胀前的不均匀种子是随机的量子涨落生成的，而CCC的不均匀性却源自前世的经典动力学演化。

将暴胀从我们“今生”的过去转移到“前世”的未来，是颇有哲学意味的。如果拿两个世代的界面（crossover）做镜像反射，那就是一个有趣的时间反演。这样看来，CCC也许可以归结为某种时间反演的模型；如果需要多个世代，只需要让反演发生在一个闭合的时空里。这令我想起埃舍尔（Escher）根据彭老师的不可能三角形创作的两幅名画：《瀑布》和《升与降》——整体上看，它们描绘了同一个空间的无限的时间循环，而局域地看，那些过程都是现实的和普通的。它们是不是CCC图景的另一种直观表达呢？（彭老师也借了埃舍尔的画，不过是为了表现“共形”。）

从理论的结构说，CCC是Weyl曲率假设的逻辑结果。如果说彭老师和霍金的奇点定理说明了奇点的存在，那么Weyl曲率假设便刻画了奇点的一个普适的基本特征。CCC就是体现这个特征的宇宙图景。与其他的循环理论（如下面说的）比起来，CCC要简单和纯粹得多。从物理内容看，它一点儿也不疯狂。它涉及的问题都是物理学的“经典”问题（如奇点问题、暗物质问题、基本粒子衰变问题、黑洞蒸发问题、信息丢失问题、量子引力问题、共形几何问题），所以不但不疯狂，而且相当“传统”。

Escher受Penrose不可能三角形创作的版画《升与降》（1960）

5.宇宙是轮回的吗？

标准的大爆炸—暴胀模型不说大爆炸“之前”，也不好意思提那样的问题。借古老的奥古斯丁的话说，上帝为那些爱打听“以前”的人准备了地狱。可现代宇宙学似乎就是从循环的宇宙模型开始的。1922年，Friedmann提出的第一个宇宙学模型就是闭合循环的。Lemaitrei很欢喜那样的场方程解：“宇宙连续地膨胀和收缩，那样的解有着不容置疑的如诗的魅力，令人想起传说中的凤凰。”可见循环是我们直觉的宇宙学图景。然而，“循环”对科学来说却不大好，有人说它是为了避免上帝的“创世纪”（genesis），Eddington干脆说他没有“凤凰崇拜”。但一直有“一小撮”科学家在研究它，当然不是为了宗教，而是为了避免奇点。

Friedmann的“循环”是从膨胀到收缩的循环，时间方向随收缩而倒转（将它作为熵规定的方向），这意味着初始奇点与终结奇点是一样的。20世纪30年代，加州理工学院的Tolman第一个提出了第二定律的协变形式及其宇宙学意义。他的循环宇宙是一个无限不可逆的膨胀—收缩序列，其中每个“世代”的熵都比前一个的大。可他对第二定律的作用也不是十分肯定——在著名的《相对论、热力学和宇宙学》中，他只是弱弱地指出：“至少我们似乎不必再武断地认为第二定律一定要求一个在有限时间生成和消亡的宇宙。”就是说，宇宙无须达到经典热力学所谓的“热寂”。不过有趣而遗憾的是，如果倒推他的那个熵增序列，最终还会回到零点，于是他的循环没能摆脱初始条件的问题。实际上，Tolman后来似乎也不大宣扬循环宇宙。

更近的循环宇宙是真正的“火凤凰”。在大约10年多前，普林斯顿的Paul Steinhardt等人根据膜理论的“火宇宙”（Ekpyortic）图像提出，宇宙经历无限多个膨胀—收缩的循环，每个循环从大爆炸开始。彭老师也提到了这个模型（3.3节），而且它与CCC的思路有相通的地方。它的基本点是：

●大爆炸不是时间的开始，而是向更早的演化相的过渡；

●宇宙的演化是循环的；

●宇宙大尺度结构的形成发生在大爆炸前的某个缓慢的收缩相，而不是大爆炸后的暴胀期。

这个宇宙建立在多维时空图景（膜世界）的基础上（尽管可以用四维的语言来描述）。它的膨胀与挤压是两个膜通过第5维相互作用的结果。两个膜发生碰撞，然后相互穿过（也可以说相互离开，因为没有膜外的世界）。那个碰撞，在膜上的人看来（我们当然在一个膜上），就是大爆炸。然后，同样通过第5维，两个膜又靠近（那个第5维仿佛一根可以随意拉伸和压缩的弹簧），于是重演先前的过程。

膜宇宙也考虑了熵的问题，仍然是通过第5维的作用：一个循环的熵随膨胀而“稀释”，密度趋于零。但在收缩期里，熵密度不再增大（因为收缩只发生在额外维）。从一个膜上的局域观测者看来，熵密度也在循环，但膜的总熵是增大的。[Paul几年前也写了一本循环宇宙的书，叫《无尽的宇宙：超越大爆炸，重写宇宙史》（Endless Universe：beyond the big bang-rewriting the cosmic history, Broadway，2008）。]

比“火凤凰”更“疯狂”的循环宇宙，大概是物质与反物质轮流“坐庄”的宇宙。最近有人提出，我们处于物质的宇宙是因为我们的“前世”是反物质的。在两个“世代”的界面，不断演绎着物质—反物质的生成和湮灭。

循环宇宙模型还有很多，以后可能还会有。它们为物理学带来了有趣而浪漫的图景，也能激发有趣而根本的新问题。抛开具体的问题不说，就有两个很根本的（多少有些形而上的味道）问题：第一，物理学方程允许宇宙循环，这本身是不是一个问题呢？第二，“无限循环”是不是真正的物理问题？如果不是，那么这些模型是用一个非物理问题来“抹平”物理问题；如果是，那么这样的“无限”岂非又堕入了新的奇点？（所谓奇点，就是出现无穷大的地方。）

6.关于本书

CCC可以说是彭老师近四十年的宇宙学思考的结果，很多概念和数学物理细节都有大量文献，但CCC本身才萌芽，本书是它的第一次系统呈现，而且迄今也没有更完备的研究论文，反倒是相关的研究论文（少得可怜）都拿它作为基本参考文献。因而，这不是一本纯粹的科普读物——很多章节的描述是十分专业的，虽然把数学公式藏起来了，读起来还是要费点儿气力，需要读者有一定的物理学基础，特别是相对论和量子（场）论的修养。当然，还需要一点儿想象力，更需要多一些耐心。

具体说来，我们可以借鉴物理学家Paul Davies学相对论的经验：相信不可能的，想象看不见的。（这个“法门”，也是王后要爱丽丝小妹妹每天做的功课。）不过，Davies也承认，有些东西是想象不来的——“不过说实在的，我与这些概念打交道，是在反复运用中熟悉的，并没有得到什么神秘的直觉力量。我相信现代物理学揭示的实在是与人类思想根本冲突的，而且令一切的想象力黯然失色。诸如‘弯曲空间’和‘奇点’之类的名词所构想的精神图像，顶多是一些残缺的模型，只是在我们的头脑里定一个题目，而不会告诉我们物理世界到底是什么样子。”（见Davies, The Matter Myth）这段话用在这本书是很恰当的。

实际上，彭老师在给一个读者的信中也承认，几何的直观想象不过是经验而已——当我们“习惯”它了，就以为能“想象”它了。对高维几何（时空），我们其实只是“看见”它在三维（欧氏空间）的投影，只是让自己相信了它，却自以为“想象”出它来了。当我们面对书中的那些共形图时，如果想象不出来，也别怪自己缺乏想象力，我们只要耐心地慢慢熟悉它们就好了。记住Davies老师说的大实话：“并不是世界上的每个事物都能通过想象力去把握的”——明白了这一点，缺乏想象力的我们是不是可以轻松一点呢？

最后说说书名。原文很简单，就是“时间的循环”（Cycles of Time），但作标题似乎不够味儿，不够刺激。cycle当然是循环，但不管从哪个意义说，它都令人想起佛家的“轮回”，而且它的确也是“轮回”的一种英译。据《不列颠百科全书》Buddhism词条，samsara（“轮回”）即the ongoing cycle of birth, death, and rebirth；《牛津英语词典》的解释是The endless cycle of death and rebirth to which life in the material world is bound，可见这个定义完全可以移到CCC来。另外，我们借精神世界的“轮回”来说物理宇宙的“循环”，不是说物理学皈依了佛门，只是想“顺便地”通过名词令读者联想一点儿现代物理学与“东方神秘主义”的平行。

译者

2013年7月28日，成都