附录
附录A 共形标度,2—旋量,麦克斯韦和爱因斯坦理论
这里的多数方程都用2—旋量形式。这倒不是必须的,其实我们也都给出了大家更熟悉的4—张量形式。不过,2—旋量形式不仅能更简单地表述共形不变的特性(见A6),也能更系统地从整体上理解无质量场的传播和相应的其构成粒子的薛定谔方程。
在写方程时,我们遵从以前的约定,包括抽象指标(参见Penrose and Rindler,1984,1986)[A.1],不过这里宇宙学常数用Λ而不用λ。那本书里的标量曲率“Λ”在这儿为R/24。方程前面的记号P&R指那部书,其实所有需要的方程都可以在第2卷中找到。这儿的爱因斯坦张量Eab是那儿的“爱因斯坦张量”Rab-Rgab/2的负值(而里奇张量Rab的符号与那儿的相同),所以爱因斯坦场方程为(见2.6节和3.5节)
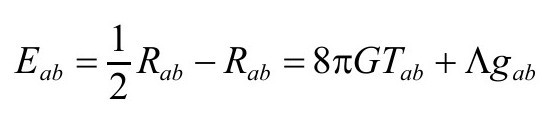
A1.2—旋量记号:麦克斯韦方程
2—旋量形式采用抽象旋量指标(在复2维旋量空间中),我用斜体大写拉丁字母,无撇的(A, B,C,……)或带撇的(A′,B′,C′,……),它们在复共轭下交换。每个时空点的复化正切空间是无撇旋量空间与带撇旋量空间的张量积。于是我们可以用抽象指标的恒等式:
a=AA′,b=BB′,c=CC′,……
其中斜体小写拉丁字母a, b,c,……指时空的正切空间。更确切说,上标的是正切空间,而下标的是余切空间。
反对称麦克斯韦场张量Fab(=-Fba)可以用对称的2—指标2—旋量φAB(=φBA)表示为2—旋量形式
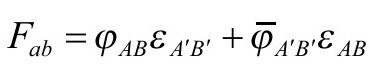
其中量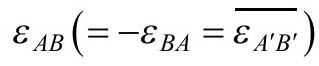 定义了旋量空间的复辛结构,通过如下抽象指标方程与度规联系:
定义了旋量空间的复辛结构,通过如下抽象指标方程与度规联系:
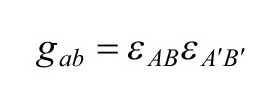
旋量指标的提升和下降遵从如下惯例(ε上的指标顺序很重要!)
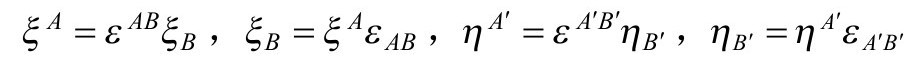
以荷流矢量Ja为场源的麦克斯韦场方程(在3.2节统写为 )
)
为
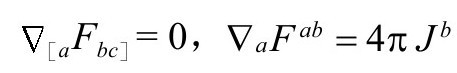
(其中指标外的方括弧表示反对称化,圆括弧表示对称化),荷流守恒方程为
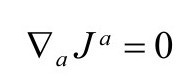
它们对应的2—旋量形式(P&R5.1.52,5.1.54)为
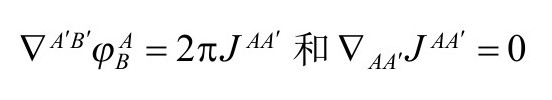
无源(Ja=0)时,我们得到自由麦克斯韦方程(3.2节写为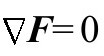 )
)
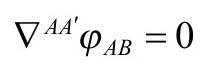
A2.无质量自由场(薛定谔)方程
最后那个方程,是自旋为n/2(>0)的无质量粒子的自由场方程(P&R4.12.42),或“薛定谔方程”[A.2]在n=2的情形
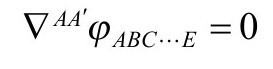
其中φABC E有n个指标,而且是全对称的:
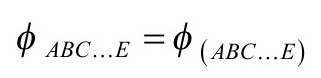
在n=0情形,场方程通常为□φ=0,这里达朗贝尔(D’Alembertian)算子□定义为
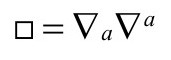
但在弯曲时空中,我们要用算子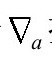 指协变微分,所以在这儿我们更喜欢用如下形式的方程(P&R6.8.30)
指协变微分,所以在这儿我们更喜欢用如下形式的方程(P&R6.8.30)
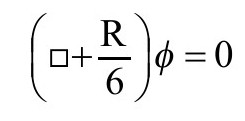
在我们将要讨论的意义上(见A6),这个方程是共形不变的。(这里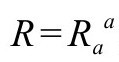 是曲率标量。)
是曲率标量。)
A3.时空曲率量
黎曼—克里斯多夫(Riemann-Christoffel)曲率张量Rabcd具有如下对称性
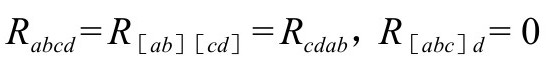
且与导数对易子有如下关系(P&R4.2.31):
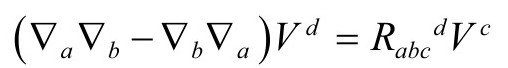
这个关系确定了Rabcd的符号约定。我们这里分别定义里奇和爱因斯坦张量和里奇标量如下:
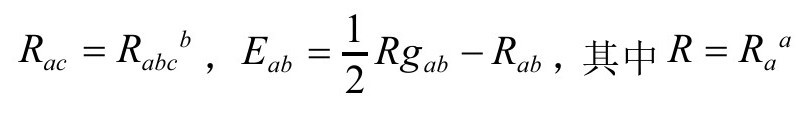
外尔共形张量Cabcd定义为(P&R4.8.2)
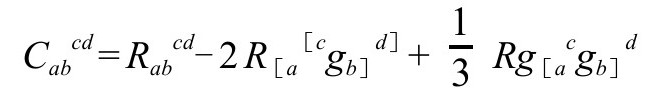
它与Rabcd有相同对称性,但所有的迹为零:
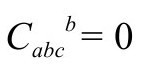
利用旋量,我们可以写成(P&R4.6.41)
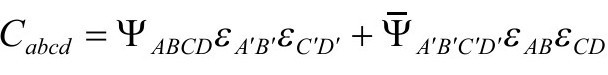
其中共形旋量ΨABCD是全对称的:
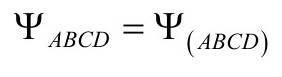
Rabcd的其他信息包含于标量曲率R和里奇(或爱因斯坦)张量的零迹部分,而后者隐含于旋量ΦABC′D′,它具有对称性与厄米性(Hermiticity):
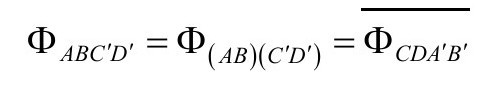
其中(P&R4.6.21)

A4.无质量引力源
在附录B,我们将特别考虑(对称)源张量Tab的迹为零
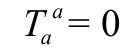
时的爱因斯坦场方程,因为这个条件正好描述无质量(即零静止质量)的引力源,告诉我们旋量指标的量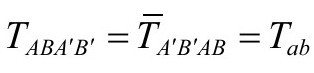 有对称性
有对称性
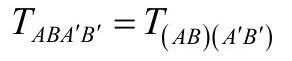
散度方程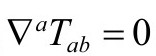 即
即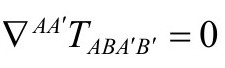 ,可以改写为
,可以改写为
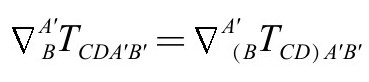
上面的爱因斯坦方程现在可以写成(P&R4.6.32)
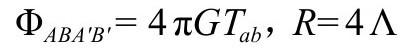
如果有静止质量,因而Tab有迹
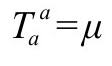
则爱因斯坦方程有如下形式
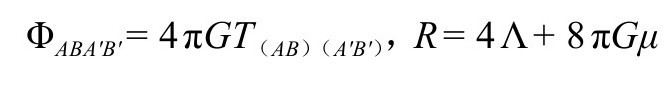
A5.毕安基恒等式
一般的毕安基(Bianchi)恒等式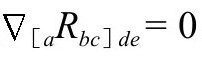 ,可以写成如下的旋量形式(P&R4.10.7,4.10.8):
,可以写成如下的旋量形式(P&R4.10.7,4.10.8):
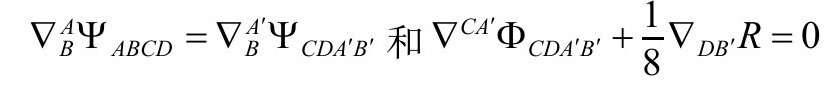
当R为常数时——无质量源的爱因斯坦方程出现的情形——我们有
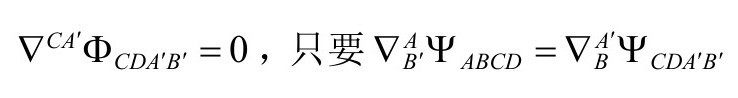
其中隐含右边关于BCD对称。结合无质量源的爱因斯坦方程,我们得到
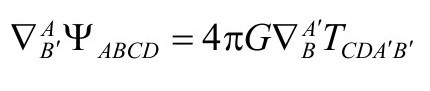
(见P&R4.10.12)注意,当TABC′D′=0时,我们有方程(P&R4.10.9)
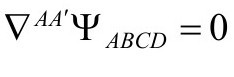
这就是A2的无质量自由场方程在n=4(即自旋2)的情形。
A6.共形标度
根据共形标度(Ω>0均匀变化)
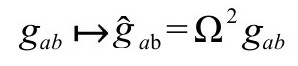
我们采用如下抽象指标关系
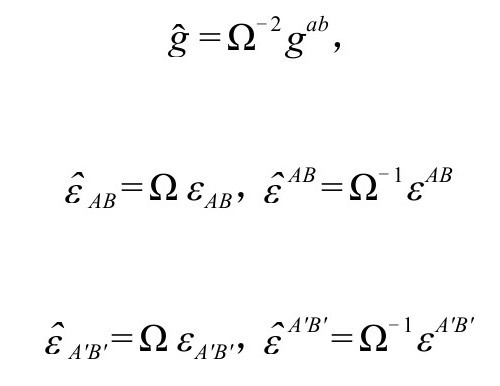
算子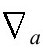 现在必须如下变换
现在必须如下变换
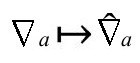
这样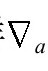 对一般以旋量指标表示的量的作用应如下生成:
对一般以旋量指标表示的量的作用应如下生成:
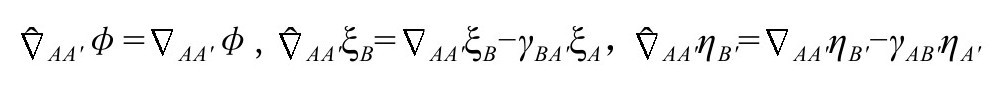
其中
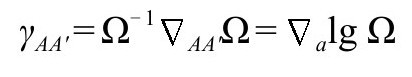
这些法则确定了我们处理多个下标的量(每个指标一项)的方式。(上标有对应处理方式,但这里不需要。)
我们选择无质量场φABC……E的标度为
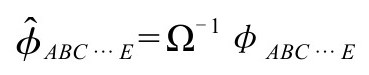
用上面的约定,我们看到
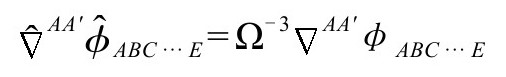
于是,不论哪边为零,另一边也为零,只要满足无质量自由场方程是标度不变的。对有源的麦克斯韦方程,我们发现整个系统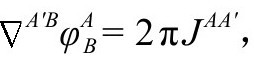
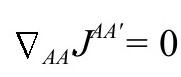 的共形不变性(见A2的P&R5.1.52,5.1.54)由下面的标度保证:
的共形不变性(见A2的P&R5.1.52,5.1.54)由下面的标度保证:

因为我们看到

A7.杨—米尔斯场
杨—米尔斯方程构成了我们当今关于基本粒子强弱相互作用的认识基础。更重要的是,只要我们忽略可以通过希格斯(Higgs)场的后续作用而生成的质量,那么这些方程也是共形不变的。杨—米尔斯场强度可以用一个张量(“丛曲率”)来表示:
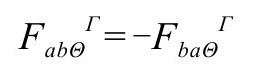
其中抽象指标Θ,Γ,……指与粒子对称性相关的内禀对称群[U(2),SU(3)或其他群]。我们可以用旋量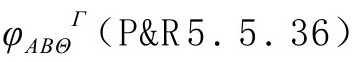 表示丛曲率:
表示丛曲率:
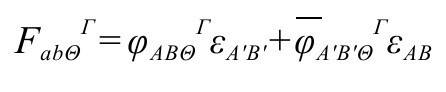
对幺正内禀群,这里内禀下标的复共轭变为内禀上标,反之亦然。场方程将其镜像反射为麦克斯韦方程,这里我们提供了额外的内禀指标。于是,麦克斯韦理论的共形不变性也适用于杨—米尔斯方程,因为内禀指标Θ,Γ,……不受共形标度的影响。
A8.零静止质量能量张量的标度
应该指出,对迹为零的能量张量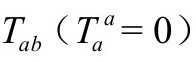 而言,我们发现标度(P&R5.9.2)
而言,我们发现标度(P&R5.9.2)
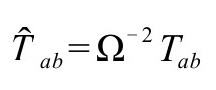
将保持守恒方程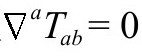 ,因为我们看到
,因为我们看到
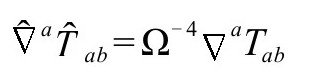
在麦克斯韦理论中,我们有一个用Fab表示的能量张量,它可以变换为如下旋量形式(P&R5.2.4)
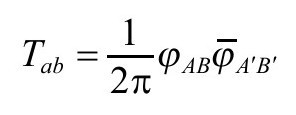
在杨—米理论的情形,我们只是多几个指标:

对无质量标量场,满足我们先前考虑的方程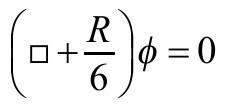 (P&R6.8.30),我们有共形不变性(P&R6.8.32)
(P&R6.8.30),我们有共形不变性(P&R6.8.32)
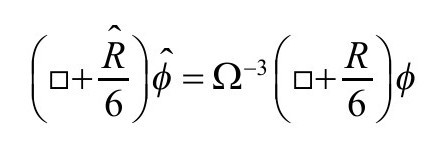
其中

其能量张量(有时称为“新改进的”[A.3])为(P&R6.8.36)
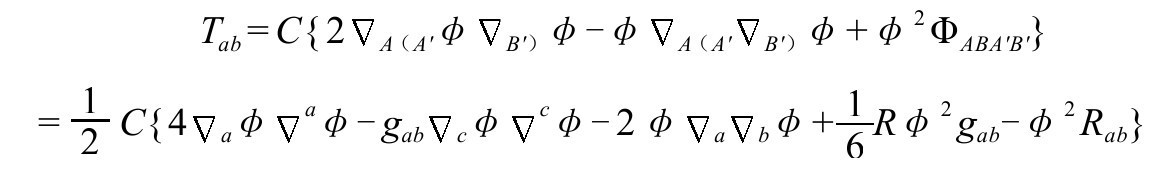
C为正常数,满足需要的条件
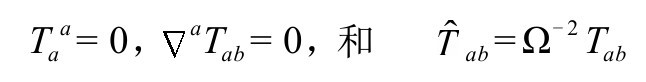
A9.外尔张量共形标度
共形旋量ΨABCD隐含了时空共形曲率的信息,是共形不变的(P&R6.8.4)
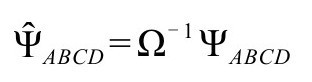
注意这里的共形不变与满足无质量自由场方程的要求,有一点奇怪(却很重要)的偏差,在那儿,右边应该多一个因子Ω-1。为融合这点偏差,我们可以定义一个处处与ΨABCD成正比的量ψABCD,其标度遵从
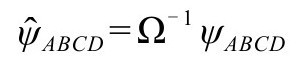
我们还发现真空(Tab=0)中引力子的“薛定谔方程”[A.4](P&R4.10.9)
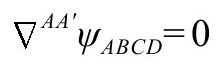
也是共形不变的。在3.2节,以上方程写作
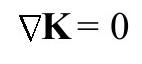
相应于外尔张量Cabcd(A3,P&R4.6.41),我们可以定义
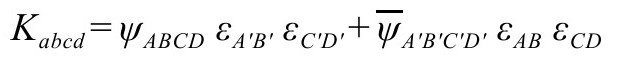
其对应的标度为(在3.2节中写作 )
)
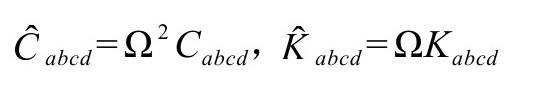
附录B 界面处的方程
和附录A一样,我们遵从以前的约定,包括抽象指标(参见Penrose and Rindler,1984,1986),不过这儿的宇宙学常数用Λ而不用λ。那部书里的标量曲率“Λ”在这儿为R/24。下面的具体分析,在某些方面是不完全的,也不是最后确定的,那些建议很可能需要改进和更完备的处理。不过,我们看来已经有了确定的经典方程,使我们能以和谐一致且完全确定的方式从一个世代的遥远未来续到下一个世代的大爆炸之后的区域。
B1.度规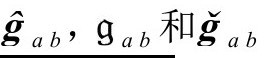
我们根据第3部分的思想,来考察穿越界面3—曲面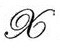 的一个邻域。我们曾假定包含
的一个邻域。我们曾假定包含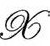 的光滑时空存在一个“颈圈”
的光滑时空存在一个“颈圈” ,它可以向
,它可以向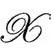 的过去和未来两个方向延伸,而在界面
的过去和未来两个方向延伸,而在界面 之前只存在无质量场。我们在颈圈内选取光滑度规
之前只存在无质量场。我们在颈圈内选取光滑度规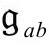 ,并至少在局域上、以某种初始任意的方式满足给定的共形结构。令爱因斯坦的物理度规在
,并至少在局域上、以某种初始任意的方式满足给定的共形结构。令爱因斯坦的物理度规在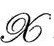 之前的4—区域
之前的4—区域 中为
中为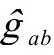 ,而在紧跟
,而在紧跟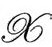 的4—区域
的4—区域 中为
中为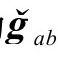 ,其中
,其中

(注意,这里与3.2节的约定不尽相同,爱因斯坦物理度规gab没有“戴帽”。不过,附录A中的具体公式仍然成立。)为方便记忆,我们不妨将符号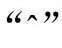 和
和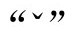 与
与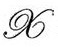 的时空点上的对应部分的零锥联系起来。在每个那样的区域里,我们假定固定宇宙学常数Λ的爱因斯坦方程成立,还假定所有引力源在更早的区域
的时空点上的对应部分的零锥联系起来。在每个那样的区域里,我们假定固定宇宙学常数Λ的爱因斯坦方程成立,还假定所有引力源在更早的区域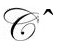 中都是无质量的,因而其能量张量
中都是无质量的,因而其能量张量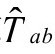 是无迹的。
是无迹的。
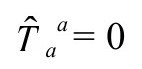
因为后面马上出现的理由,我用不同的字母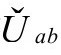 来表示
来表示 中能量张量,而且会看到(为了保持形式的一致),这个张量实际上将获得一个很小的迹
中能量张量,而且会看到(为了保持形式的一致),这个张量实际上将获得一个很小的迹
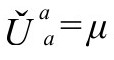
这样,在 中会出现一个能量张量的静止质量分量。可以猜想,这与Higgs机制的静止质量生成有关[B.1],但这里不探讨那个思想。(应该指出,“戴帽”的量,如
中会出现一个能量张量的静止质量分量。可以猜想,这与Higgs机制的静止质量生成有关[B.1],但这里不探讨那个思想。(应该指出,“戴帽”的量,如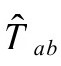 等等,分别通过
等等,分别通过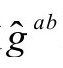 和
和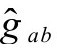 ,或相应的
,或相应的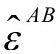 ,
,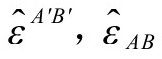 和
和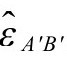 ,而“反戴帽子”的量,如
,而“反戴帽子”的量,如 ,则通过
,则通过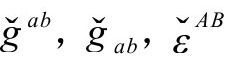 和
和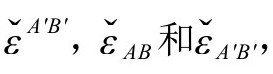 提升或下降其指标。)爱因斯坦方程分别在区域
提升或下降其指标。)爱因斯坦方程分别在区域 和
和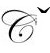 成立,于是我们有“戴帽”和“反戴帽”的形式:
成立,于是我们有“戴帽”和“反戴帽”的形式:
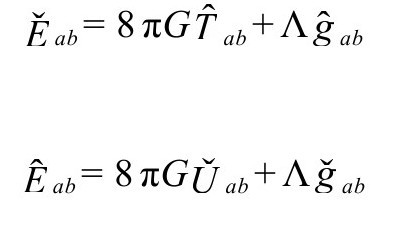
这里我假定两个区域有相同的宇宙学常数[B.2],于是
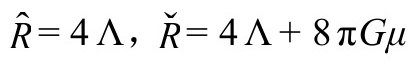
这时,跨3维穿越界面 的度规
的度规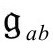 是完全自由选择的,但是光滑的,而且与给定的
是完全自由选择的,但是光滑的,而且与给定的 和
和 的共形结构一致。然后,我提出一个建议,它看起来能以某种正则而恰当的方式唯一确定度规
的共形结构一致。然后,我提出一个建议,它看起来能以某种正则而恰当的方式唯一确定度规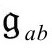 的标度,这样就可以最终选定一个确定的
的标度,这样就可以最终选定一个确定的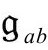 ,我用标准的斜体记号“gab”来表示。另外,不论
,我用标准的斜体记号“gab”来表示。另外,不论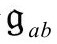 是否确定为gab,我都用标准的斜体符号来表示曲率量Rabcd等。
是否确定为gab,我都用标准的斜体符号来表示曲率量Rabcd等。
B 2.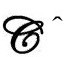 的方程
的方程
下面,我先考虑区域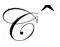 的方程,然后再处理区域
的方程,然后再处理区域 见B11)。我们可以将爱因斯坦(和里奇)张量的变换法则(P&R6.8.24)写成
见B11)。我们可以将爱因斯坦(和里奇)张量的变换法则(P&R6.8.24)写成
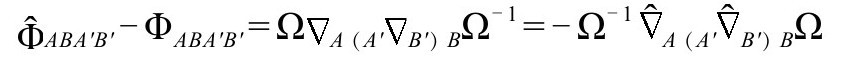
和(P&R6.8.25)
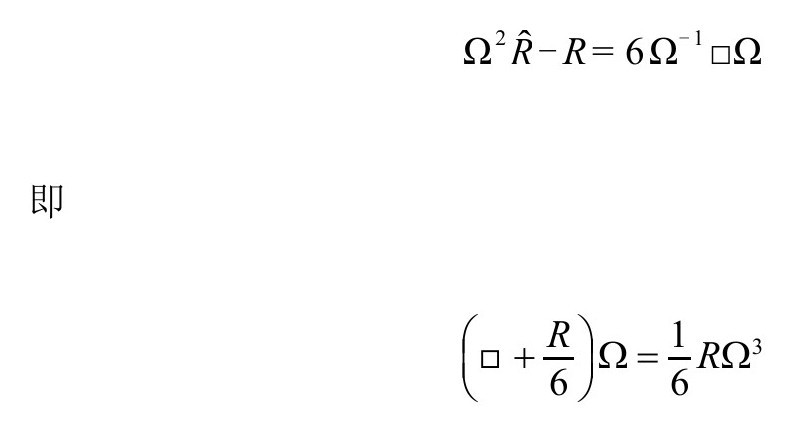
最后这个方程有着特别的纯数学趣味,是所谓的卡拉比(Calabi)方程的一个例子[B.3]。但它也有物理学的意义,是一个共形不变自耦合标量场ϖ的方程,在R=4Λ,可以写成
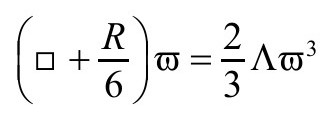
我将在下面说明,这个“ϖ方程”的每个解为我们提供一个新度规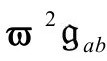 ,其标量曲率有常数值4Λ。ϖ方程的共形不变性体现在如下事实:如果我们选择一个新共形因子
,其标量曲率有常数值4Λ。ϖ方程的共形不变性体现在如下事实:如果我们选择一个新共形因子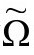 ,并从gab变换到新共形相关的度规
,并从gab变换到新共形相关的度规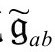 ,
,
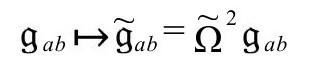
那么ϖ场的共形标度
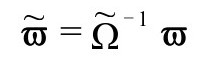
给我们如下方程(A8已经说过;见P&R6.8.32)
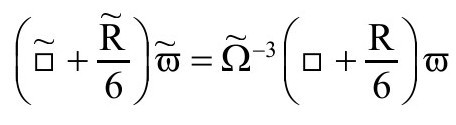
由此可直接得到我们需要的非线性ϖ方程的标度不变性。(注意,当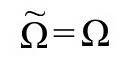 和ϖ=Ω时,我们回到爱因斯坦的
和ϖ=Ω时,我们回到爱因斯坦的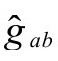 度规,
度规,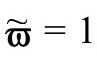 ,方程变成恒等式
,方程变成恒等式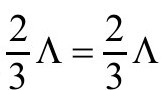 。)
。)
我们在A8看到,对这样的一个物理ϖ场,其能量张量在无ϖ3项时为(P&R6.8.36)
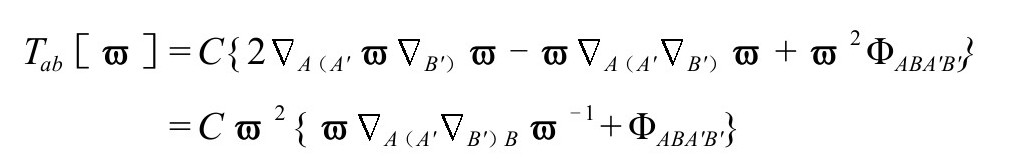
其中C为常数。而且,我们还发现在ϖ方程中,ϖ3项不会破坏守恒方程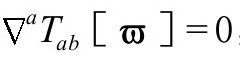 ,所以我们也用它来表达ϖ场的能量张量;为与下面的讨论一致,我选择
,所以我们也用它来表达ϖ场的能量张量;为与下面的讨论一致,我选择
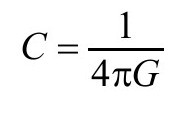
与上面(P&R6.8.24,B2)比较,我们从度规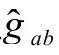 的爱因斯坦方程
的爱因斯坦方程
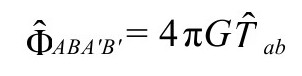
看到
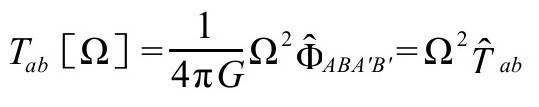
对无迹的能量张量,我们看到标度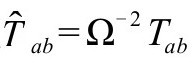 (A8,P&R5.92)保持守恒方程,于是我们得到一种多少有些令人惊奇的爱因斯坦理论的新形式:对无质量引力源Tab,关于
(A8,P&R5.92)保持守恒方程,于是我们得到一种多少有些令人惊奇的爱因斯坦理论的新形式:对无质量引力源Tab,关于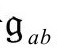 度规的方程为
度规的方程为
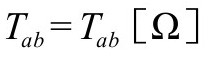
B3.幽灵场的作用
Ω可以看作无质量自耦合共形不变场ϖ的一个特殊情形,我称它为幽灵场[B.4]。它没有提供在物理上独立的自由度,其出现(在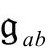 度规下)只是允许我们进行自由标度,从而重新标度物理度规而获得一个与爱因斯坦度规共形的光滑度规
度规下)只是允许我们进行自由标度,从而重新标度物理度规而获得一个与爱因斯坦度规共形的光滑度规 ,光滑地覆盖相邻世代之间的每一个交集。有了这样一个覆盖3维跨界曲面的度规,我们就能通过具体的经典微分方程,详细研究满足CCC要求的世代之间的确定联络。
,光滑地覆盖相邻世代之间的每一个交集。有了这样一个覆盖3维跨界曲面的度规,我们就能通过具体的经典微分方程,详细研究满足CCC要求的世代之间的确定联络。
幽灵场的角色就是告诉我们如何标度度规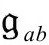 回到物理度规(通过
回到物理度规(通过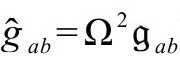 ),从而“跟踪”爱因斯坦真实的物理度规。这样,我们可以说爱因斯坦方程在前一世代的界面空间
),从而“跟踪”爱因斯坦真实的物理度规。这样,我们可以说爱因斯坦方程在前一世代的界面空间 成立,不过这时用度规
成立,不过这时用度规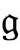 来表达为Tab=Tab[Ω];就是说,我们表达爱因斯坦方程,要求时空区域
来表达为Tab=Tab[Ω];就是说,我们表达爱因斯坦方程,要求时空区域 内的所有物理场(假定无质量且有正确的共形标度)的总能量张量Tab必须等于幽灵场的能量张量Tab[Ω]。尽管可以简单把这看作爱因斯坦理论的新形式(用
内的所有物理场(假定无质量且有正确的共形标度)的总能量张量Tab必须等于幽灵场的能量张量Tab[Ω]。尽管可以简单把这看作爱因斯坦理论的新形式(用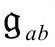 ),但它还有更微妙的东西。它允许我们将方程拓展到甚至超越它的未来边界
),但它还有更微妙的东西。它允许我们将方程拓展到甚至超越它的未来边界 。但是,为了有效实现这一点,我们需要更仔细地考察相关物理量的方程和它们在接近
。但是,为了有效实现这一点,我们需要更仔细地考察相关物理量的方程和它们在接近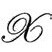 时的预期行为。而且,我们还需要认识并且清除
时的预期行为。而且,我们还需要认识并且清除 度规(即共形标度Ω)的自由度——那起初是为了我们感兴趣的“颈圈”
度规(即共形标度Ω)的自由度——那起初是为了我们感兴趣的“颈圈” 而多少有些随意地选择的。
而多少有些随意地选择的。
就眼下情形,共形标度Ω确实有一个值得关注的自由度。迄今为止,我们需要Ω满足如下条件:从爱因斯坦物理度规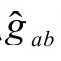 得到的度规
得到的度规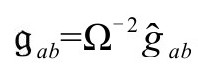 在穿过
在穿过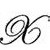 时是有限、非零且光滑的。尽管如此要求Ω的存在显得有些过分,Helmut Friedrich[B.5]也得到过很强的结果,使我们可以预期,在正宇宙学常数时,在无质量源的完全膨胀宇宙模型中,无质量辐射场的所有自由度都包含在光滑(类空)的
时是有限、非零且光滑的。尽管如此要求Ω的存在显得有些过分,Helmut Friedrich[B.5]也得到过很强的结果,使我们可以预期,在正宇宙学常数时,在无质量源的完全膨胀宇宙模型中,无质量辐射场的所有自由度都包含在光滑(类空)的 之中。换句话说,我们相信可以找到
之中。换句话说,我们相信可以找到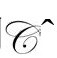 的一个光滑未来共形边界
的一个光滑未来共形边界 ,这是无限膨胀模型的一个多少有些自然的结果,其中所有引力源都遵从共形不变方程传播的无质量场。这里应该指出,不需要度规
,这是无限膨胀模型的一个多少有些自然的结果,其中所有引力源都遵从共形不变方程传播的无质量场。这里应该指出,不需要度规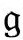 的标量曲率R为常数,当然更不需要R=4Λ,于是带我们回到爱因斯坦
的标量曲率R为常数,当然更不需要R=4Λ,于是带我们回到爱因斯坦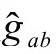 度规的共形因子Ω-1不必满足
度规的共形因子Ω-1不必满足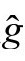 度规下的ϖ方程
度规下的ϖ方程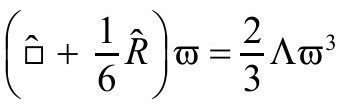 。
。
B 4. 的法向量N
的法向量N
我们看到,从下面趋近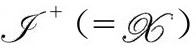 时,Ω→∞,因为Ω的作用就是为
时,Ω→∞,因为Ω的作用就是为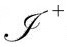 处的有限度规
处的有限度规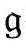 提供一个无限大的标度,变成前一个世代的遥远未来。然而,我们发现量
提供一个无限大的标度,变成前一个世代的遥远未来。然而,我们发现量
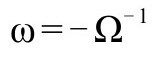
以光滑的方式(因为下面的理由,负号是必须的)从下面趋于零,从而使

在3维界面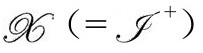 上非零,于是为我们在
上非零,于是为我们在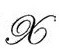 的时空点上提供了
的时空点上提供了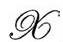 的未来方向的类时4维法向量N。
的未来方向的类时4维法向量N。
我们的意思是,让这个特殊的“ω”连续光滑地从区域 通过
通过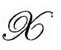 进入区域
进入区域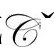 ,而且有非零导数,从而真正变成同样的(正的)量“ω”(因为这一点,“ω=-Ω-1”中的负号是必须的)。还应该指出,“正规化”条件(P&R9.6.17)
,而且有非零导数,从而真正变成同样的(正的)量“ω”(因为这一点,“ω=-Ω-1”中的负号是必须的)。还应该指出,“正规化”条件(P&R9.6.17)
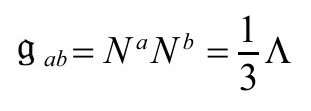
在只有无质量源引力场时,是共形无限远(这里即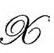 )的一个自动的一般性质,于是
)的一个自动的一般性质,于是
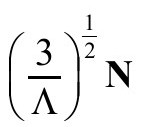
是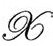 的单位法向量,与共形因子的特殊选择无关。
的单位法向量,与共形因子的特殊选择无关。
B5.事件视界区域
顺便说一句,我们看到可以很容易从这儿导出3.5节中提到的一个事实:任意宇宙学事件视界的截面的极限面积必然等于12π/Λ。任何事件视界(在前一个世代的)都是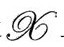 上某个永恒观测者的未来终点o+的过去光锥
上某个永恒观测者的未来终点o+的过去光锥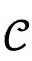 ,与2.5节说的一样(见图2.43)。于是,从下面趋近o+时,
,与2.5节说的一样(见图2.43)。于是,从下面趋近o+时,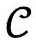 的截面的极限面积为4πr2,这里r(在g度规下)是截面的空间半径。在
的截面的极限面积为4πr2,这里r(在g度规下)是截面的空间半径。在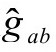 度规的情形,这个面积为4πr2Ω2;我们还容易从以上的讨论(B4)看到,当截面趋近o+时,Ωr的极限趋于
度规的情形,这个面积为4πr2Ω2;我们还容易从以上的讨论(B4)看到,当截面趋近o+时,Ωr的极限趋于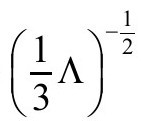 ,于是我们需要的事件视界的面积实际上等于4π×(3/Λ)=12π/Λ。(尽管论证是在CCC背景下进行的,我们所要求的只是类空共形无限远具有很小程度的光滑性,正如Friedrich证明的,[B.6]这在Λ>0时是一个很弱的假定。)
,于是我们需要的事件视界的面积实际上等于4π×(3/Λ)=12π/Λ。(尽管论证是在CCC背景下进行的,我们所要求的只是类空共形无限远具有很小程度的光滑性,正如Friedrich证明的,[B.6]这在Λ>0时是一个很弱的假定。)
B6.倒数建议
我们的特殊情形当然存在缺陷:在描述从 到
到 的过渡时,不论Ω还是ω,我们都没有光滑变化的量——它们以均匀的方式描述回到爱因斯坦度规
的过渡时,不论Ω还是ω,我们都没有光滑变化的量——它们以均匀的方式描述回到爱因斯坦度规
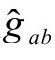
和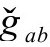 的标度。但恰当解决这个问题,需要利用前面提到过的倒数建议ω=-Ω-1,然后我们很方便考虑如下定义的1—形式
的标度。但恰当解决这个问题,需要利用前面提到过的倒数建议ω=-Ω-1,然后我们很方便考虑如下定义的1—形式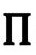 :
:
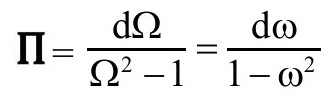
即
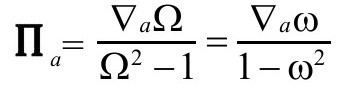
只要我们坚持倒数建议所蕴含的假设,这个1—形式在穿过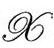 时是有限而连续的。这个量
时是有限而连续的。这个量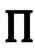 包含了时空的度规标度信息,尽管(必然)有些许的模糊。[B.7]我们可以综合出一个参数τ,使
包含了时空的度规标度信息,尽管(必然)有些许的模糊。[B.7]我们可以综合出一个参数τ,使
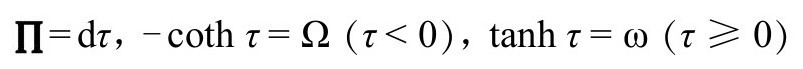
我们看到,即使这儿也有符号改变的老问题,因为尽管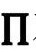 对以Ω-1取代Ω(或ω-1取代ω)并不敏感,但从Ω-1到ω还是有符号改变。不管怎么说,我们可以认为共形因子的符号无关紧要,因为在
对以Ω-1取代Ω(或ω-1取代ω)并不敏感,但从Ω-1到ω还是有符号改变。不管怎么说,我们可以认为共形因子的符号无关紧要,因为在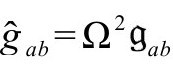 和
和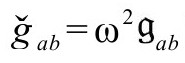 的新标度中,共形因子Ω和ω是以平方出现的,所以即使用正号而不用负号,也可以认为只是一个习惯问题。不过,正如我们在附录A中说的,还有很多量是用非平方的Ω(或ω)标度的,最突出的是标度
的新标度中,共形因子Ω和ω是以平方出现的,所以即使用正号而不用负号,也可以认为只是一个习惯问题。不过,正如我们在附录A中说的,还有很多量是用非平方的Ω(或ω)标度的,最突出的是标度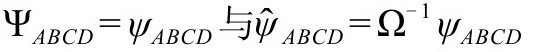 之间的差别,导致在空间
之间的差别,导致在空间 中
中
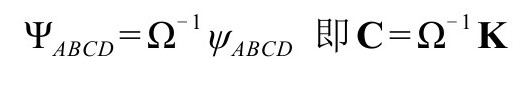
因为那儿的爱因斯坦物理度规为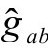 ,使我们有
,使我们有
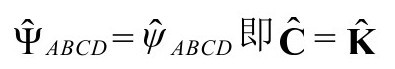
(这个约定不同于我们在3.2节的约定,因为现在爱因斯坦方程是在戴帽的度规下成立的。)于是,考虑到物理量在穿过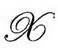 的光滑行为(Ω和ω分别在通过∞和0时改变符号),我们必须小心跟踪这些符号的物理意义。
的光滑行为(Ω和ω分别在通过∞和0时改变符号),我们必须小心跟踪这些符号的物理意义。
然而,这里利用的Ω和ω之间明确的倒数关系依赖于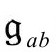 度规标度的严格选择,即满足条件
度规标度的严格选择,即满足条件
R=4Λ
正相应于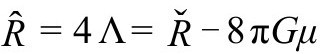 见B1)。这个标度至少很容易局域地调整,只需要为
见B1)。这个标度至少很容易局域地调整,只需要为 选一个新的(局域的)度规
选一个新的(局域的)度规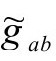 ,满足
,满足
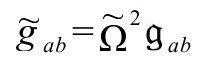
其中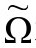 是ϖ方程在界面的光滑解。但是,ϖ方程有很多可能的
是ϖ方程在界面的光滑解。但是,ϖ方程有很多可能的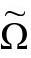 解可以选择,所以这个
解可以选择,所以这个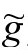 度规还不是我们寻找来以正则方式覆盖界面的唯一g度规。我们马上将看到需要度规
度规还不是我们寻找来以正则方式覆盖界面的唯一g度规。我们马上将看到需要度规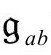 满足的进一步的要求。现在,我们只假定
满足的进一步的要求。现在,我们只假定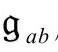 度规的选择满足R=4Λ(即我们重新将上面的
度规的选择满足R=4Λ(即我们重新将上面的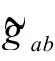 作为
作为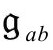 的新选择)。如果没有R=4Λ的限制,Ω和ω之间的倒数关系就不可能精确,尽管对我们指望从托德建议[B.8](见2.6节的末尾和3.1,3.2节)寻找的那种类型的标度因子ω来说,在以纯辐射为引力源的大爆炸情形(与托尔曼的充满辐射的解一样,见3.3节)[B.9],标度因子在趋近过去的大爆炸极限时,其行为真就像与前一个世代的某个Ω标度因子的光滑延拓的倒数成正比。对
的新选择)。如果没有R=4Λ的限制,Ω和ω之间的倒数关系就不可能精确,尽管对我们指望从托德建议[B.8](见2.6节的末尾和3.1,3.2节)寻找的那种类型的标度因子ω来说,在以纯辐射为引力源的大爆炸情形(与托尔曼的充满辐射的解一样,见3.3节)[B.9],标度因子在趋近过去的大爆炸极限时,其行为真就像与前一个世代的某个Ω标度因子的光滑延拓的倒数成正比。对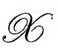 中的
中的 的度规,选择R=4Λ,就是为了将这个比例因子固定为(-)1。这一点可以用下面的事实来说明:关系
的度规,选择R=4Λ,就是为了将这个比例因子固定为(-)1。这一点可以用下面的事实来说明:关系
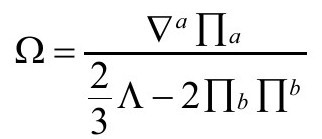
依赖于对共形因子Ω的限定,即要求它转换为其倒数的负数ω=-1/Ω而不是(例如)-A/Ω。上面的关系多少有些令人惊奇,它出现在我们用散度算子 作用于
作用于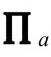 ,然后用Ω的ϖ—方程。当这个限制用于R,即选择
,然后用Ω的ϖ—方程。当这个限制用于R,即选择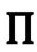 的某个特殊形式[而不是一般的形式,如dΩ/(Ω2-A)]时,就会有上面的关系。注意在
的某个特殊形式[而不是一般的形式,如dΩ/(Ω2-A)]时,就会有上面的关系。注意在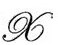 那儿Ω=∞),我们必须有
那儿Ω=∞),我们必须有
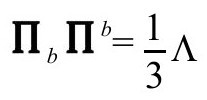
还有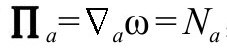 ,即
,即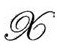 的法向长度为
的法向长度为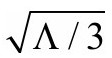 ,正如前面指出的(P&R9.6.17)。
,正如前面指出的(P&R9.6.17)。
B 7.跨 的动力学
的动力学
凭什么相信我们的动力学方程允许我们以毫不含糊的方式穿过 呢?我假定爱因斯坦方程在前一世代的遥远未来成立,不过所有的源都是无质量的,而且遵从确定的决定性的共形不变的经典方程演进。我们可以假定那些方程是麦克斯韦方程、无质量的杨—米尔斯方程和狄拉克—外尔类型的方程
呢?我假定爱因斯坦方程在前一世代的遥远未来成立,不过所有的源都是无质量的,而且遵从确定的决定性的共形不变的经典方程演进。我们可以假定那些方程是麦克斯韦方程、无质量的杨—米尔斯方程和狄拉克—外尔类型的方程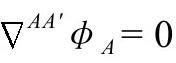 狄拉克方程的零质量极限),有些粒子作为规范场的源,根据§3.2,在静止质量趋于零时,它们都取极限形式。它们与引力场的耦合,表达在方程Tab=Tab[Ω]中,其中Ω是幽灵场。我们知道,Tab[Ω]在
狄拉克方程的零质量极限),有些粒子作为规范场的源,根据§3.2,在静止质量趋于零时,它们都取极限形式。它们与引力场的耦合,表达在方程Tab=Tab[Ω]中,其中Ω是幽灵场。我们知道,Tab[Ω]在 应该是有限的,尽管Ω在那儿是无限大,因为Tab本身在
应该是有限的,尽管Ω在那儿是无限大,因为Tab本身在 应该是有限的,蕴涵在Tab中的场的传播是共形不变的,因而与
应该是有限的,蕴涵在Tab中的场的传播是共形不变的,因而与 在
在 中的位置没有特别的关系。CCC的建议是,只要情形不会变得更复杂,例如通过希格斯机制(或其他什么更准确的可能方式)从寻常的引力源获取质量,那么那些物质源的同样的共形不变方程一定会延续到大爆炸之后的区域
中的位置没有特别的关系。CCC的建议是,只要情形不会变得更复杂,例如通过希格斯机制(或其他什么更准确的可能方式)从寻常的引力源获取质量,那么那些物质源的同样的共形不变方程一定会延续到大爆炸之后的区域 。不过,我们将看到,在穿过
。不过,我们将看到,在穿过 之后不久,即使对那种罕见的假想情形,我们也不能避免静止质量以某种形式出现(见B11)。
之后不久,即使对那种罕见的假想情形,我们也不能避免静止质量以某种形式出现(见B11)。
B8.共形不变Dab算子
为理解场源对 的物理意义,认识那个区域的爱因斯坦方程是如何运行的,我们先来具体看看Tab[Ω]:
的物理意义,认识那个区域的爱因斯坦方程是如何运行的,我们先来具体看看Tab[Ω]:
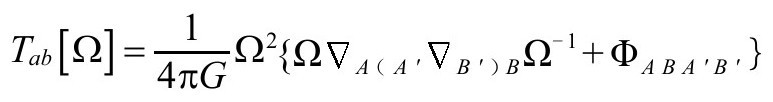
因为ω=-Ω-1,它可以写成
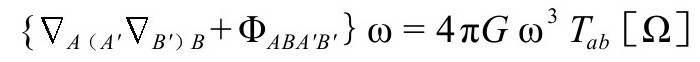
这是一个有趣的方程,趣味就在于左边的2阶算子
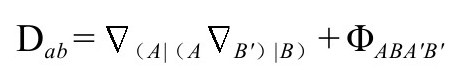
作用于共形权重为1的标量时(这儿的算子作用于标量时,AB的额外对称不起作用),是共形不变的——最早指出这一点的是Eastwood和Rice。[B.10]它可以用张量表示为(用Rab的符号约定)
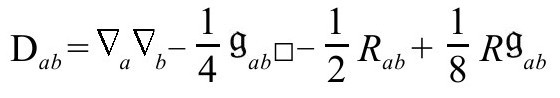
量ω确实有共形权重1,因为假如 依照
依照
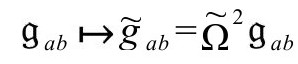
进一步重新标度,然后用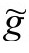 度规下的
度规下的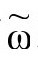 定义来镜像反射
定义来镜像反射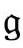 度规下的ω,
度规下的ω,

则我们看到
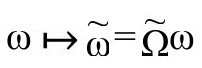
(即ω有共形权重1)。于是
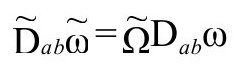
我们可以用算子形式来表示这个共形不变性
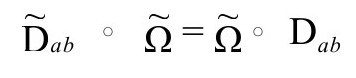
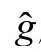 度规的爱因斯坦方程,可用以上算子用
度规的爱因斯坦方程,可用以上算子用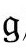 度规写出来:
度规写出来:
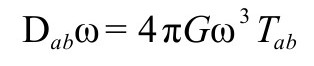
它告诉我们,如果Tab(我们相信)在穿过 时是光滑的,则量Dabω本身在穿过
时是光滑的,则量Dabω本身在穿过 时必然在3阶项为零。特别是,Dabω=0在
时必然在3阶项为零。特别是,Dabω=0在 上为零的事实告诉我们,
上为零的事实告诉我们,
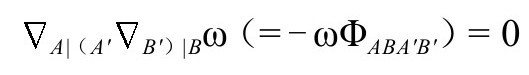
我们还可以将它重写为(在 上)
上)

(其中,和B4一样,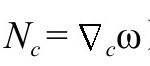 ),它告诉我们
),它告诉我们 的法向在
的法向在 上是“无剪切的”,这是
上是“无剪切的”,这是 在它的每一点都是“脐点”的条件。[B.11]
在它的每一点都是“脐点”的条件。[B.11]
B9.保持引力常数为正
如果考察无质量引力源场(如Tab描述的)与引力场(或“引力子场”)ψABCD之间的的相互作用(如A5的方程P&R4.10.12,“戴帽”形式的或用ω=-Ω-1写的),我们可以更好地理解CCC所蕴涵的物理意义。我们有
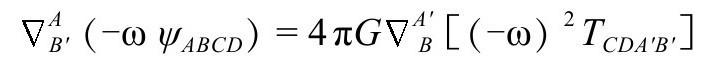
我们可以由此导出等价的方程,用“戴帽”的量,可以写成
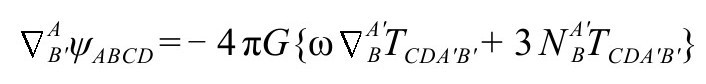
我们看到,当ω光滑通过零(由负变正)时,这个方程还保持着良好的行为。这说明了一个事实:决定整个系统演化的一族方程,在 度规下,从
度规下,从 通过
通过 到
到 时,确实不会遇到困难。
时,确实不会遇到困难。
想象我们在进入 时回到原来的
时回到原来的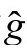 度规。于是(除了在
度规。于是(除了在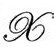 的初始“脉冲”),经典方程呈现给我们的时空
的初始“脉冲”),经典方程呈现给我们的时空 的演化图像,将是一个坍缩的宇宙模型,以反指数方式从无限远向内收缩,看起来很像我们自己宇宙的遥远未来的样子。不过,这儿有一个重要的解释问题,因为当ω改变符号(从负到正)时,“有效引力常数”(特别看上面公式里的-Gω,当ω变大时,右边第一项将起主导作用)在穿过
的演化图像,将是一个坍缩的宇宙模型,以反指数方式从无限远向内收缩,看起来很像我们自己宇宙的遥远未来的样子。不过,这儿有一个重要的解释问题,因为当ω改变符号(从负到正)时,“有效引力常数”(特别看上面公式里的-Gω,当ω变大时,右边第一项将起主导作用)在穿过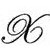 时会改变符号。[B.12]CCC为我们提供的另一个解释是,考虑到与量子场论的一致性等因素,关于早期
时会改变符号。[B.12]CCC为我们提供的另一个解释是,考虑到与量子场论的一致性等因素,关于早期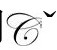 区域的物理的特殊解释(具有负引力常数),在引力相互作用变得重要时,不可能以物理方式保持下来。相反,CCC的观点是,当我们继续深入
区域的物理的特殊解释(具有负引力常数),在引力相互作用变得重要时,不可能以物理方式保持下来。相反,CCC的观点是,当我们继续深入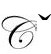 区域时,用
区域时,用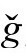 度规提供的物理解释更为恰当,这时,当下的正共形因子ω取代了当下的负共形因子Ω,有效引力常数也就又变成正数了。
度规提供的物理解释更为恰当,这时,当下的正共形因子ω取代了当下的负共形因子Ω,有效引力常数也就又变成正数了。
B10.清除虚假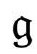 度规自由度
度规自由度
这里生出一个问题:根据CCC的要求,我们需要唯一的进入 的演化。假如没有共形因子的随意性产生的令人讨厌的多余自由度,这本来是不成问题的。眼下,这种自由给我们带来一个虚假的自由度,它会不恰当地影响
的演化。假如没有共形因子的随意性产生的令人讨厌的多余自由度,这本来是不成问题的。眼下,这种自由给我们带来一个虚假的自由度,它会不恰当地影响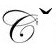 的非共形不变的引力动力学。为了让通过
的非共形不变的引力动力学。为了让通过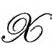 的演化独立于非
的演化独立于非 的物理所决定的那些额外条件,我们需要清除虚假的自由度。在
的物理所决定的那些额外条件,我们需要清除虚假的自由度。在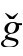 度规选择中的虚假“规范自由”可以表示为一个共形因子
度规选择中的虚假“规范自由”可以表示为一个共形因子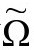 ,它可以用于
,它可以用于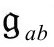 而为我们提供一个新的
而为我们提供一个新的 度规(与我们前面的度规一致):
度规(与我们前面的度规一致):
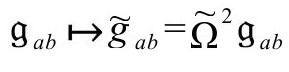
和前面一样,我们在这儿用了

到此为止,我们只要求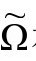 是
是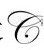 上(至少在局域碎片上)光滑变化的正值标量场,满足
上(至少在局域碎片上)光滑变化的正值标量场,满足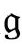 度规的ϖ方程——这个要求是为了满足标量曲率
度规的ϖ方程——这个要求是为了满足标量曲率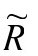 保持为4Λ。ϖ方程是标准的二阶双曲方程,所以我们指望能得到
保持为4Λ。ϖ方程是标准的二阶双曲方程,所以我们指望能得到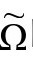 的
的
唯一解(在足够细小的颈圈 内),只要
内),只要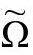 的值和它的法向导数的值都能确定为
的值和它的法向导数的值都能确定为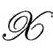 上的光滑函数。如果我们知道如何选择这些值才能得到某个具有独特性质的
上的光滑函数。如果我们知道如何选择这些值才能得到某个具有独特性质的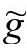 度规,那么结果是直截了当的。于是问题来了:我们该为度规限定什么条件,才能清除这些虚假的自由度?
度规,那么结果是直截了当的。于是问题来了:我们该为度规限定什么条件,才能清除这些虚假的自由度?
然而,我们无法做到为 度规强加一个条件(也许还需要
度规强加一个条件(也许还需要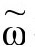 场),让它能共形不变且能保持
场),让它能共形不变且能保持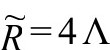 标度。这样,考虑一个平凡的例子,我们不能根据我们的需要而要求
标度。这样,考虑一个平凡的例子,我们不能根据我们的需要而要求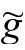 度规的标量曲率
度规的标量曲率 具有任何4Λ以外的数值,而要求它恰好具有4Λ的值也不代表对任何场的任何附加条件,因而不能作为进一步的限制来消减我们想清除的虚假自由度。同样的情形(更微妙)也适用于我们对法向的限制:我们不能要求
具有任何4Λ以外的数值,而要求它恰好具有4Λ的值也不代表对任何场的任何附加条件,因而不能作为进一步的限制来消减我们想清除的虚假自由度。同样的情形(更微妙)也适用于我们对法向的限制:我们不能要求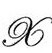 的法向量
的法向量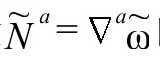 的平方长度
的平方长度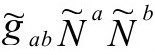 具有某个特别的数值(指标用
具有某个特别的数值(指标用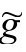 度规升降)。因为,假如我们选择任何一个不同于Λ/3的值,那么(如前面看到的,见P&R9.6.17)这个条件不可能满足;而如果所选数值真是Λ/3,那么条件不代表任何对虚假自由的限制。
度规升降)。因为,假如我们选择任何一个不同于Λ/3的值,那么(如前面看到的,见P&R9.6.17)这个条件不可能满足;而如果所选数值真是Λ/3,那么条件不代表任何对虚假自由的限制。
同样的问题还出现在诸如
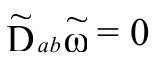
的要求,它不代表限定共形因子的任何条件,因为共形不变性(前面说过)满足
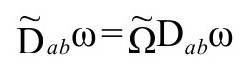
这样,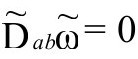 等价于
等价于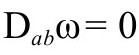 。这样说来,像
。这样说来,像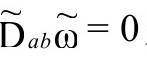 那样的条件,无论如何是没有意义的,因为存在几个分量,而我们所要求的东西只代表
那样的条件,无论如何是没有意义的,因为存在几个分量,而我们所要求的东西只代表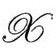 的每个点的两个条件(如在那点确定的
的每个点的两个条件(如在那点确定的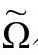 及其法向导数)。而且,还可以看到(正如上面说的),因为关系
及其法向导数)。而且,还可以看到(正如上面说的),因为关系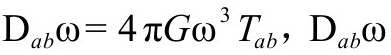 在
在 必然在3阶以上消失,即
必然在3阶以上消失,即
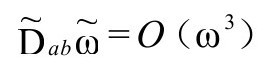
然而,一个看似合理的条件也许是,可以要求在 上
上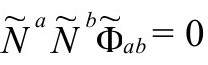 。更确切说,我们可以将此建议写成
。更确切说,我们可以将此建议写成
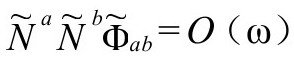
实际上,我们可以要求这个量在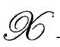 上在2阶消失,即
上在2阶消失,即

它可能为我们提供一个合适的候选条件,以满足我们为了确定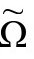 (从而通过
(从而通过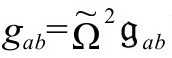 确定g度规)而对
确定g度规)而对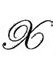 的每一点的两个要求。根据Dab的定义,这些可能条件将等价于要求
的每一点的两个要求。根据Dab的定义,这些可能条件将等价于要求

用张量记号,以上两个不同表达式为
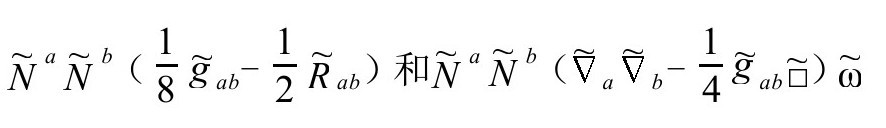
这里我们注意(去掉波浪线)

我们还看到
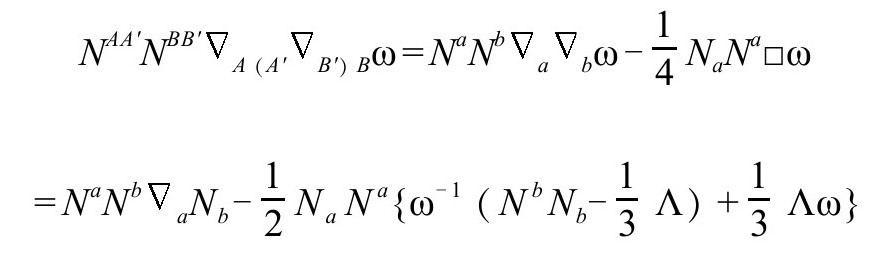
这意味着,我们可以添加的一个(或一对)合理条件为
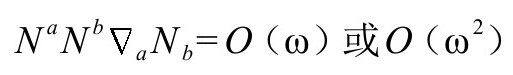
它能大为简化上面的条件(这里注意,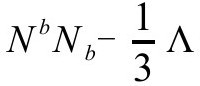 分别在2阶和3阶为零)。反过来,如果在
分别在2阶和3阶为零)。反过来,如果在 上
上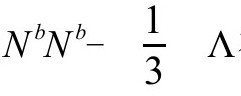 在2阶和3阶为零,那么在
在2阶和3阶为零,那么在 上
上
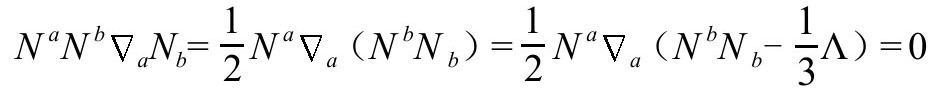
所以,不管哪个等价条件[以形式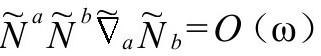 或
或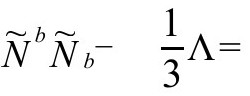
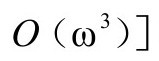 都可以认为是我们要求
都可以认为是我们要求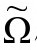 应满足的条件。注意,前面B 6给出的关系
应满足的条件。注意,前面B 6给出的关系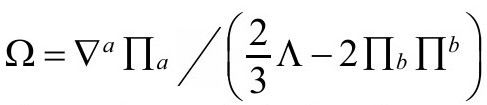 要求Ω在
要求Ω在 上有一个简单极点,于是,如果分母2阶为零,分子
上有一个简单极点,于是,如果分母2阶为零,分子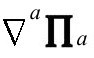 必然是1阶为零的,实际上,
必然是1阶为零的,实际上,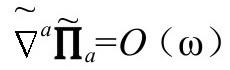 也是一个可能的附加条件形式,根据B8,我们可以想到,当
也是一个可能的附加条件形式,根据B8,我们可以想到,当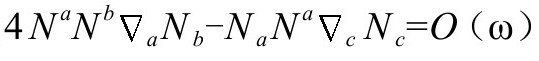 时,在
时,在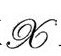 上有
上有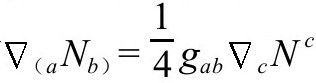 。
。
在下面B11将看到,根据我们的程序, 的能量张量Uab必然会得到迹μ,这意味着会出现静止质量的引力源。然而,我们发现迹在
的能量张量Uab必然会得到迹μ,这意味着会出现静止质量的引力源。然而,我们发现迹在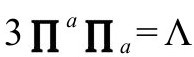 时消失。可以说,当我们尽可能延迟静止质量在大爆炸之后的出现时,CCC的思想会得到最好的落实。相应地,我们还可以认为
时消失。可以说,当我们尽可能延迟静止质量在大爆炸之后的出现时,CCC的思想会得到最好的落实。相应地,我们还可以认为
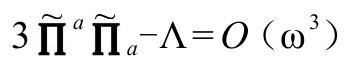
为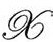 的每一点确定了两个恰当的数字,从而可以固定g度规。其实我们还发现
的每一点确定了两个恰当的数字,从而可以固定g度规。其实我们还发现
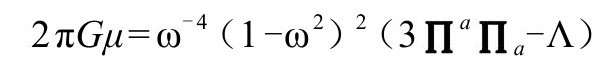
如果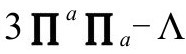 的零点不是至少为4阶的,上式将在
的零点不是至少为4阶的,上式将在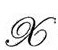 变成无限大。但这不是问题,因为μ只出现在
变成无限大。但这不是问题,因为μ只出现在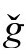 度规,其中
度规,其中 代表奇异大爆炸,在那儿,其他无限曲率量将超越μ起主导作用,只要我们取
代表奇异大爆炸,在那儿,其他无限曲率量将超越μ起主导作用,只要我们取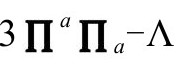 的零点是3阶的。
的零点是3阶的。
我们看到,为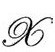 的每一点附加两个条件,有几种不同的可能,这样我们能以唯一的方式确定
的每一点附加两个条件,有几种不同的可能,这样我们能以唯一的方式确定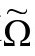 ,从而确定g度规。我写本书时,还没能完全确定最恰当的条件(也不知道其中哪些条件独立于其他的条件)。不过,正如前面说的,我倾向
,从而确定g度规。我写本书时,还没能完全确定最恰当的条件(也不知道其中哪些条件独立于其他的条件)。不过,正如前面说的,我倾向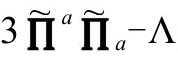 是3阶为零的。
是3阶为零的。
B11. ˇ的物质
ˇ的物质
为了看清我们的方程在后大爆炸区域
里像什么样子,我们必须用“反帽子”量,以度规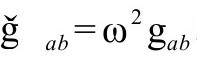 和Ω=ω-1重写方程。前面说过,我将后大爆炸的总能量张量写成Uab,以避免混淆于共形复标度的从
和Ω=ω-1重写方程。前面说过,我将后大爆炸的总能量张量写成Uab,以避免混淆于共形复标度的从 进入
进入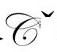 的(无质量)物质的能量张量:
的(无质量)物质的能量张量:
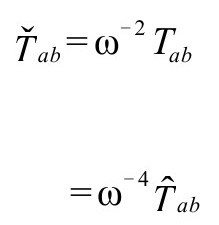
因为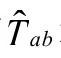 是无迹和无散度的,
是无迹和无散度的,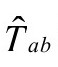 也必然如此(标度遵从A8):
也必然如此(标度遵从A8):
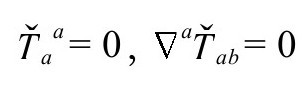
我们将看到,全部后大爆炸能量张量一定包含两个额外的无散度分量,所以
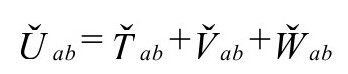
这里,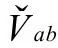 是无质量场,它应该是幽灵场Ω,现在变成了一个实在的
是无质量场,它应该是幽灵场Ω,现在变成了一个实在的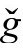 度规的自耦合共形不变场,因为这时ϖ=Ω满足
度规的自耦合共形不变场,因为这时ϖ=Ω满足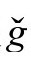 度规的ϖ方程:
度规的ϖ方程:
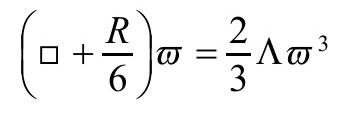
这是必须的,因为ϖ方程是共形不变的,并在g度规下满足ϖ=-1(在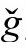 度规下即变成ϖ=-ω-1=Ω)。前面我们考虑
度规下即变成ϖ=-ω-1=Ω)。前面我们考虑 ,将“幽灵场”Ω看作ϖ方程在
,将“幽灵场”Ω看作ϖ方程在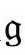 度规下的一个解,只将它解释为将我们带回物理的爱因斯坦
度规下的一个解,只将它解释为将我们带回物理的爱因斯坦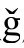 度规的标度因子;而刚才讲的,正是反过来看问题。在那个度规里,幽灵场只是“1”,因而没有独立的物理内容。现在,我们考虑Ω为爱因斯坦度规
度规的标度因子;而刚才讲的,正是反过来看问题。在那个度规里,幽灵场只是“1”,因而没有独立的物理内容。现在,我们考虑Ω为爱因斯坦度规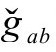 下的一个实在的物理场,而它作为共形因子的解释要反过来了,因为它告诉我们如何回到g度规,在那个度规下,场将为“1”。为了这个解释,共形因子ω和Ω互为倒数是必须的——尽管我们还需要将负号包括进来。这样,还是-Ω给我们带来了从
下的一个实在的物理场,而它作为共形因子的解释要反过来了,因为它告诉我们如何回到g度规,在那个度规下,场将为“1”。为了这个解释,共形因子ω和Ω互为倒数是必须的——尽管我们还需要将负号包括进来。这样,还是-Ω给我们带来了从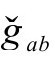 回到gab的标度。这个“逆转”的解释满足方程,因为在恰当度规下满足ϖ方程的是Ω而不是ω。
回到gab的标度。这个“逆转”的解释满足方程,因为在恰当度规下满足ϖ方程的是Ω而不是ω。
相应地,张量Vab是场Ω在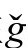 度规下的能量张量:
度规下的能量张量:
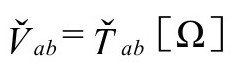
我们看到
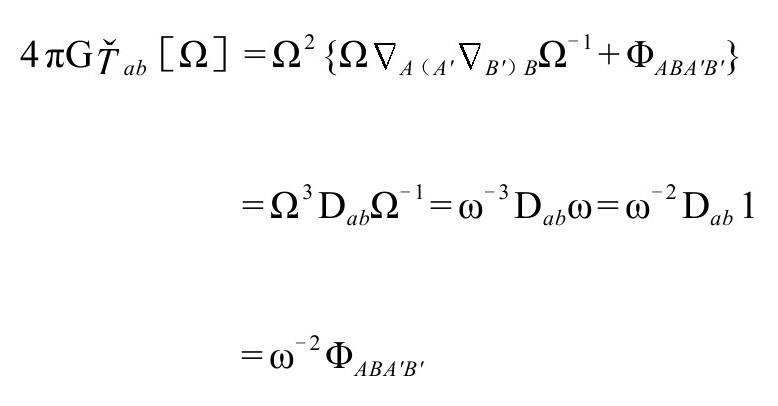
注意它具有迹和散度为零的性质:

重要的是,ω在g度规下满足的方程不是ϖ方程,因为我们已经看到,满足那个方程的是Ω,即乘以(-1)ω的倒数,从而
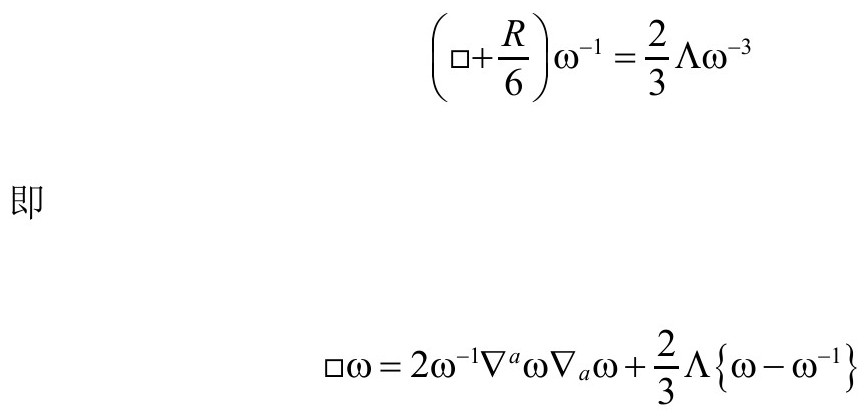
相应地,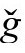 度规的标量曲率不限于等于4Λ。相反,我们有(见B2,P&R6.8.25,A4):
度规的标量曲率不限于等于4Λ。相反,我们有(见B2,P&R6.8.25,A4):
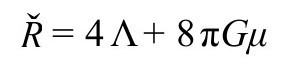
且
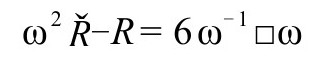
于是
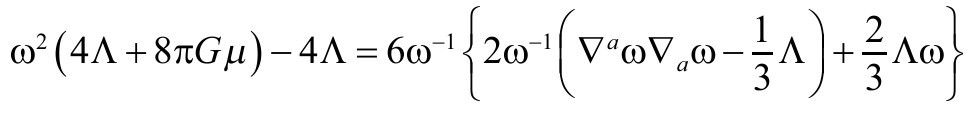
由此我们导出(见B6)
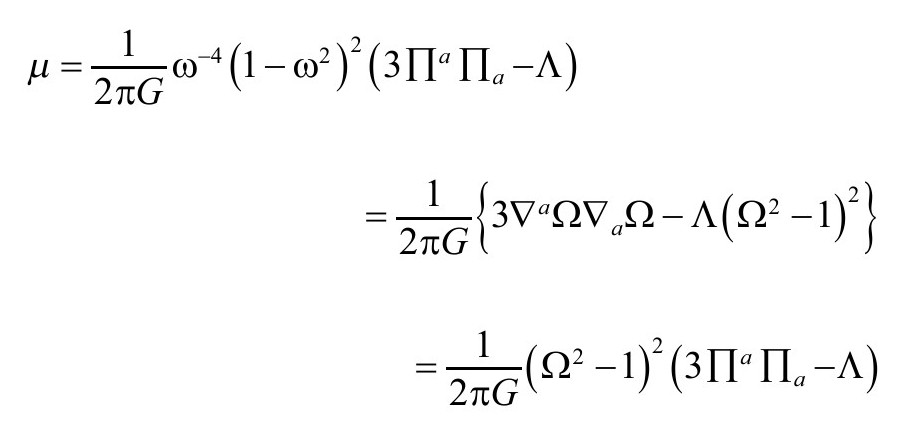
全能量张量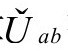 满足爱因斯坦方程,所以,除了
满足爱因斯坦方程,所以,除了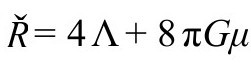 外,我们还有
外,我们还有
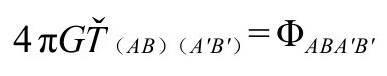
因为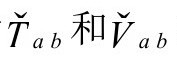 都是无迹的,需要
都是无迹的,需要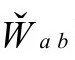 把迹找回来:
把迹找回来:
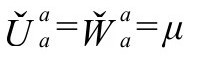
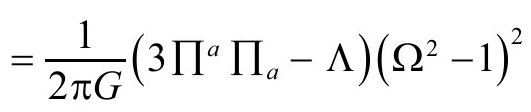
假定以上关于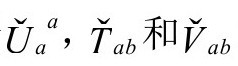 的表达式,我们可以计算
的表达式,我们可以计算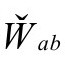 如下:
如下:
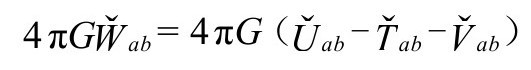
从而得到下面关于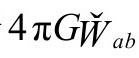 的表达式:
的表达式:
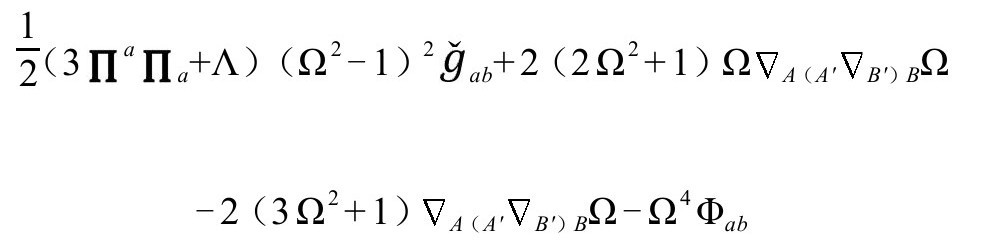
它需要进一步解释。
B12. 的引力辐射
的引力辐射
无限共形标度的度规的一个特征在于,当我们从 度规为
度规为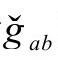 )通过
)通过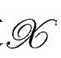 度规为gab)到
度规为gab)到 度规为
度规为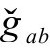 )时,引力的自由度(初始时在
)时,引力的自由度(初始时在 度规下用ψABCD描述,通常在
度规下用ψABCD描述,通常在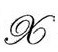 非零)以什么方式转换成
非零)以什么方式转换成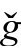 度规下的其他量。因为我们有(A9,P&R6.8.4)
度规下的其他量。因为我们有(A9,P&R6.8.4)
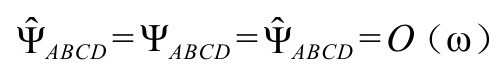
共形行为
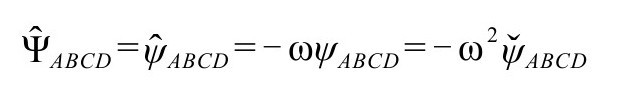
告诉我们
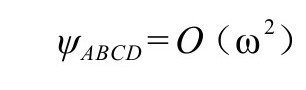
从而引力辐射在大爆炸中被大大地抑制了。
然而,在 中由ψABCD描述的引力辐射的自由度并没留下它们在早期阶段的
中由ψABCD描述的引力辐射的自由度并没留下它们在早期阶段的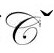 的印记。为看清这一点,我们指出,微分如下关系
的印记。为看清这一点,我们指出,微分如下关系
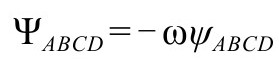
可得到
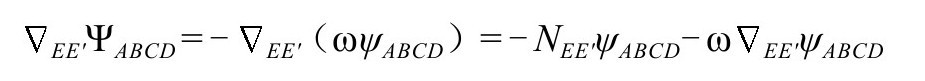
于是,即使外尔曲率在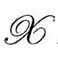 为零,它的法向导数还是提供了在
为零,它的法向导数还是提供了在 的引力辐射(无引力子)的度量:
的引力辐射(无引力子)的度量:
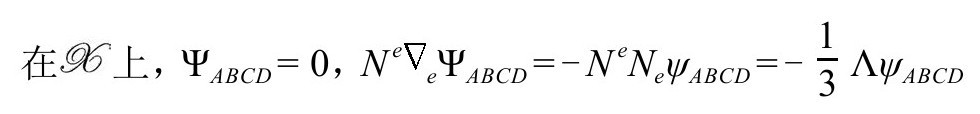
另外,根据Bianch恒等式(A5,P&R4.10.7,4.10.8)
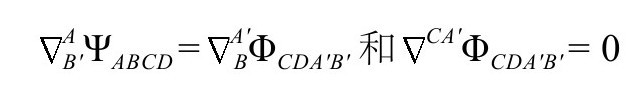
我们有
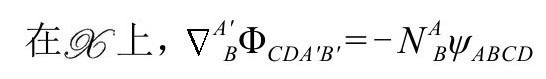
由此
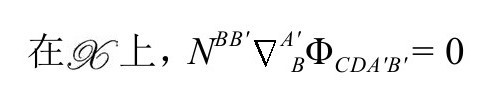
算子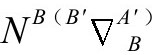 切向地作用于
切向地作用于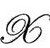 (因为
(因为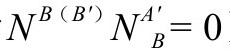 ),所以这个方程代表了一个约束,限定ΦCDA′B′在
),所以这个方程代表了一个约束,限定ΦCDA′B′在 上的行为方式。我们还看到
上的行为方式。我们还看到
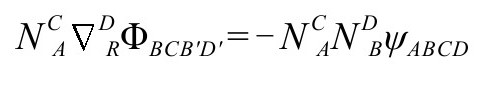
由此可见,外尔张量在 的法向导数的电部分
的法向导数的电部分

基本上是在 上的
上的

而磁部分
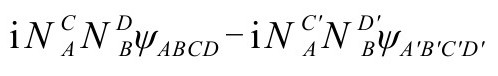
根本上就是在上 的
的

(εabcd是斜对称Levi-Civita张量),这就是描述 的内禀共形曲率的Cotton(-York)张量。[B.13]
的内禀共形曲率的Cotton(-York)张量。[B.13]
