第10章　曲率波

引力波把黑洞碰撞的交响曲带给地球，

物理学家设计出仪器来寻找那些波，

倾听它们的音乐

交响

10亿年前，在离地球10亿光年远的一个星系的中心，紧密聚集着一个几亿颗恒星和气体的集团。当一颗颗恒星被抛出去后，留下的1亿颗恒星落向中心，集团逐渐收缩，1亿年后，收缩到几光年大小，小恒星也开始零星碰撞、结合，形成更大的恒星。大恒星燃尽它们的燃料，然后坍缩形成黑洞；一对对的黑洞相互靠近，有时落入对方的轨道。

图10.1画了这样一个黑洞的双星系统的嵌入图。每个黑洞在嵌入的表面上形成深坑（强大的时空曲率），当黑洞相互绕着对方旋转时，转动的坑产生曲率波，以光速向外传播。波动在黑洞周围的时空体形成螺旋的波纹，那样子很像花园里高速旋转的浇水器喷出的水。每一滴水都会近似地沿半径飞出，同样，每一点曲率也都会向外辐射开去；向外飞出的水滴形成一条螺旋水线，因此，所有的曲率波也在时空体上形成螺旋的峰谷。

图10.1两个黑洞组成的“双星系统”轨道“平面”空间曲率的嵌入示意图。中心的两个坑代表黑洞周围的强烈时空弯曲。这样的坑在以前的黑洞嵌入图（如图7.6）中已经遇见过了。当黑洞互相围绕对方转动时，会产生向外传播的曲率波动，叫引力波。[加利福尼亚理工学院LIGO计划提供。]

因为时空曲率与引力是同一件事，所以这些曲率的波动实际上就是引力的波动，或者说引力波。爱因斯坦的广义相对论不容争辩地预言，当两个黑洞或者两颗恒星相互绕着对方转动时，一定会产生这样的引力波。

向外面空间传播的引力波会对黑洞产生反冲，就像射出去的子弹对枪的反冲一样。波的反冲作用使黑洞靠得更近，转得更快；也就是说，黑洞将螺旋式地慢慢落向对方。这个过程会逐渐释放引力能，一半进入引力波，另一半提高黑洞的转动速度。

黑洞的螺旋式运动先很慢，但随着它们越靠越近，会越动越快，它们辐射出的曲率波越强，失去的能量也越多，而螺旋式下落也越快[图10.2（a），（b）]。最后，当每个黑洞接近光速时，它们的视界便在接触中结合在一起。原来有两个黑洞的地方，现在只有一个——快速旋转的哑铃型黑洞[图10.2（c）]。当视界旋转时，哑铃辐射出曲率波，波反作用在黑洞上，将哑铃的凸起一点点削去[图10.2（d）]，留下一个赤道断面完全光滑而圆的旋转的黑洞视界，正好是爱因斯坦场方程的克尔解所描述的形状（第7章）。

我们不可能有什么办法从最后这个光滑的黑洞发现它的历史，也不可能区分它是两个小黑洞聚合形成的，还是一颗物质恒星或者一颗反物质恒星直接坍缩形成的。黑洞没有能泄露它历史的“毛”（第7章）。

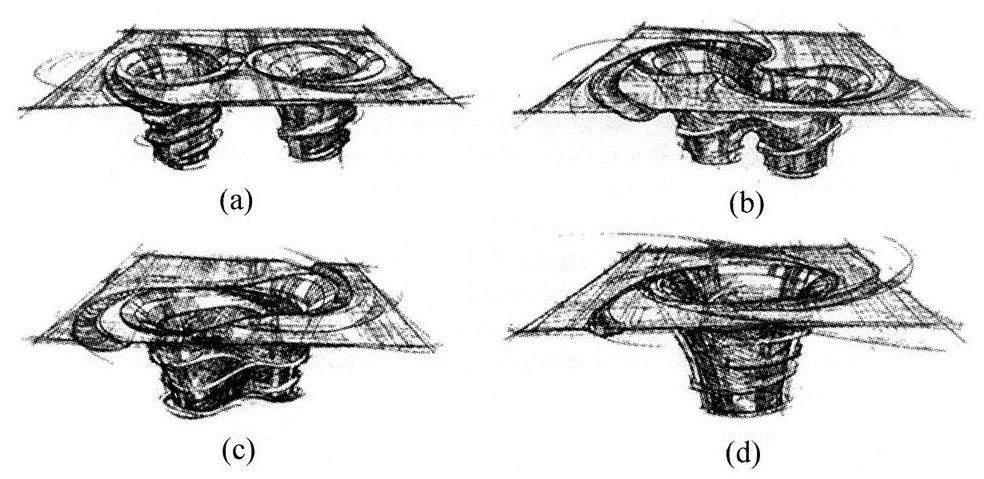
图10.2两个黑洞组成的“双星系统”周围空间曲率的嵌入示意图。图经过艺术家修饰，看起来很有动感。两个黑洞螺旋式地靠近，这些图表现了这个时间序列。在图（a）和（b），黑洞视界在坑底还是两个圆，它们在图（c）前消失而形成单独的一个哑铃型的视界。旋转的视界发出引力波，也带走了变形，留下一个光滑旋转的克尔黑洞，见图（d）。[加利福尼亚理工学院LIGO计划提供。]

然而，历史没有完全失去，还留下一点儿记录：记录在黑洞结合所发出的时空曲率波里。这些曲率波很像交响音乐的声波。音乐的交响表现在声音的强弱短长（这儿声音大，那儿声音小；这儿频率高，那儿频率低）；黑洞结合的历史也表现在曲率波的大小高低。声波带着交响乐从乐队流向听众；曲率波也带着它的历史从结合的黑洞飞向遥远的宇宙。

曲率波从两个黑洞诞生的恒星和气体的集团里出来，在时空体里穿行，既不会被吸收，也不会受干扰，完好地保留着历史的记忆。它穿过自己的星系，进入星系际空间；穿过它的星系所在的星系团，然后穿过一个又一个的星系团，来到我们的星系团，我们的银河系，我们的太阳系，最后穿过我们的地球，继续飞向更遥远的星系。

聪明的人类应该能在这些时空曲率波经过时监测到它们；我们的计算机可以将这些曲率波转换成声波，让我们听到黑洞的交响曲：当它的音调逐渐升高变强时，黑洞在螺旋地接近；然后我们听到它疯狂的回旋，那是两个黑洞正在结合成一个变形的黑洞；然后，它拖着长音慢慢地消逝，就像黑洞的凸起慢慢地收缩、消失。

从这支波澜交响曲，我们能听出很多信息：

1.我们仿佛听到一个声音在说，“我来自螺旋式结合在一起的两个黑洞。”这是绝对确凿的黑洞信号，天文学家一直在徒劳地用光、X射线（第8章）和无线电波（第9章）寻找这样的信号。因为光、X射线和无线电波在远离黑洞视界的外面，从一类完全不同于黑洞组成（纯时空曲率）的物质（高速热电子）产生出来，在穿过中间物质时会遭受严重的破坏，所以它们不能携带多少关于黑洞的信息，更不可能有什么确定的信号。相反，曲率波（引力波）来自结合黑洞视界的邻近，是由与黑洞同样的物质（时空结构的弯曲）产生的，不会遭受传播途中物质的破坏，所以，它们能为我们带来具体的关于黑洞的消息和确凿的黑洞信号。

2.这支波澜交响曲能告诉我们，每个黑洞有多重，它们旋转有多快，它们的轨道是圆还是直，它们在天空什么地方，它们离地球有多远。

3.交响曲还表现了螺旋黑洞的时空曲率的部分特征，我们能第一次确定性地检验广义相对论的黑洞预言：交响曲所表现的图景与爱因斯坦场方程的克尔解一致吗（第7章）？它所表现的旋转黑洞附近的旋涡是克尔解要求的吗？旋涡的数量与克尔解的相同吗？旋涡在接近视界时像克尔解说的那样变化吗？

4.交响曲还表现了两个黑洞视界的结合和结合的黑洞的振荡——这些事情我们今天也只有很模糊的认识。因为爱因斯坦广义相对论定律与它们相关的那个特征，我们还理解得太少，那就是所谓非线性的特征（卡片10.1）。“非线性”意味着大曲率本身还要产生曲率，它反过来又产生更大的曲率——像雪崩，下滑的一点儿雪带动周围的雪，它们又带动更多的雪，最后一坡的雪都滑落下来。我们认识非线性在宁静黑洞的表现，它是把黑洞黏结在一起的“胶”。但我们不知道，当强大的曲率剧烈动荡时，非线性在做什么：它如何表现？产生什么效应？为了认识它们，两个黑洞的结合与振荡是很有希望的“实验室”。为了认识它们，还需要实验物理学家和理论物理学家并肩协作，监测来自遥远宇宙的结合黑洞的交响波澜，在超大规模计算机上模拟它们的结合。

卡片10.1

非线性及其结果

如果一个量的总体是部分之和，我们就称它是线性的；否则，它就是非线性的。

我的家庭收入是线性的：它是妻子和我自己的薪水之和。我退休以后的养老金是非线性的，它不是我过去投入的总和；相反，它远比那个和大，因为每一笔投入都有利息，而每一点利息又会为自己带来利息。

下水道的水量是线性的，它是每家倒进管道的水的总和。雪崩的体积是非线性的，一点儿雪能够诱发一山坡的雪崩落。

线性现象简单，好分析，好预测。非线性现象复杂，难分析，难预测。线性现象只有很少的几种行为方式，很容易分门别类。非线性现象五花八门——科学家和工程师们近几年在遇到被称为混沌的非线性行为时，才开始认识它们。（混沌思想的优美引导，请看格莱克（Gleick）1987年的书。^[319]）

时空曲率小（如在太阳系）时，近似为线性的，例如，地球上海洋潮汐就是月亮和太阳的时空曲率（潮汐引力）联合作用的结果。相反，时空曲率大（如在大爆炸或黑洞附近）时，爱因斯坦广义相对论引力定律预言，曲率是高度非线性的——是宇宙中极端非线性现象之一。然而，目前我们几乎还不能说明引力非线性特征的实验和观测数据，我们解爱因斯坦方程的能力还低得可怜，我们的解只有在很简单的情况下——例如，在宁静的旋转黑洞附近，才说明了一点非线性的东西。

宁静黑洞因为引力的非线性而存在；离开引力的非线性，黑洞自身都不能维持，就像木星上的大红斑，如果没有气体的非线性行为，也不能存在下去。当生成黑洞的坍缩恒星消失在黑洞视界里时，它也失去了以任何方式影响黑洞的能力。最重要的是，恒星的引力不再是黑洞的维持者。这时候，黑洞还能继续存在完全是因为引力的非线性：没有了恒星，黑洞时空曲率仍将继续产生其非线性。这样，自我生成的曲率像非线性“胶”一样将黑洞粘在一起。

宁静黑洞激起了我们的兴趣，我们也还想知道更多：引力的非线性还产生了别的什么现象吗？通过监测和解读结合黑洞所产生的时空曲率波，也许能得到一些答案，我们在那儿大概会遇到从没想到过的混沌和奇异行为。

为了认识它们还需要监听曲率的交响乐。怎么听呢？关键在于曲率的物理本质：时空曲率与潮汐引力是同一回事。月亮产生的时空曲率在地球上激起海潮[图10.3（a）]；同样，引力波的时空曲率也能激起海潮[图10.3（b）]。

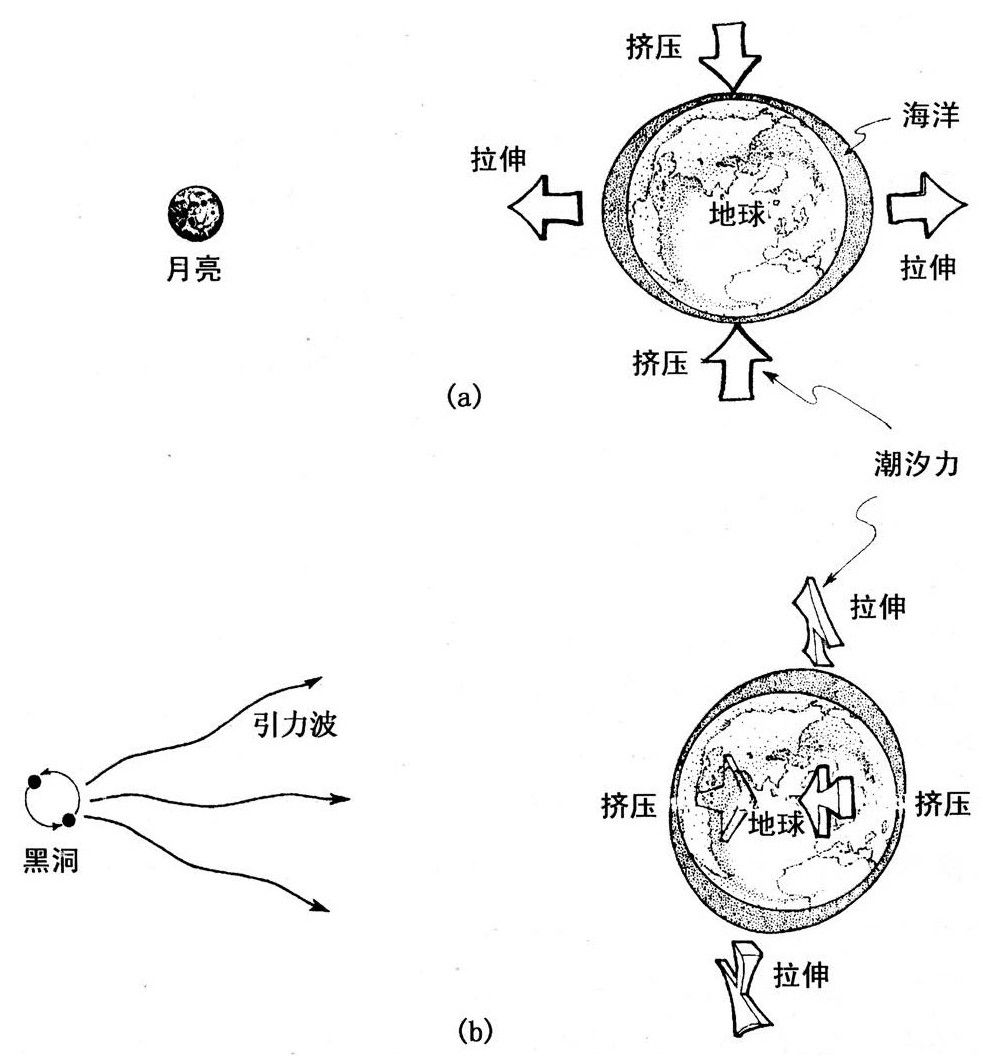
图10.3月亮和引力波产生的潮汐力。

（a）月亮的潮汐力在地球上引起的海洋潮汐的涨落：纵向涨潮，横向落潮。

（b）引力波的潮汐力引起海洋潮汐的涨落。力完全是横向的，在一个方向上拉伸，另一个方向上挤压

然而，广义相对论认为，月亮激起的海潮与引力波激起的海潮有三点不同。第一点，传播不同。引力波的潮汐力（曲率波）类似于光波和无线电波，它们从源地以光速传向地球，在传播中振荡。而月亮的潮汐力像带电物体的电场。电场紧紧依附在带电体上，带着电场的物体就像刚毛耸立的刺猬；月亮的潮汐力也是这样的，像从月亮伸出数不清的手，随时准备捕获、挤压或拉伸走近它的事物。月亮的潮汐力在地球海洋中引起的潮涨潮落似乎每过几个小时就会改变，那只是因为地球在引力场中转动。假如地球不转动，潮汐力的作用是不会改变的。

第二点，潮汐方向不同[图10.3（a），（b）]。月亮在空间所有方向都产生潮汐力。它在纵向（指向或背离月亮方向）上掀起海潮，在横向（垂直于月亮方向）上挤压地球。相反的是，引力波在纵向（沿着波传播的方向）上不产生任何潮汐力。然而，在横向平面上，引力波会在一个方向[在图10.3（b）中是上下方向]上拉伸，在另一个方向（在图中是前后方向）上挤压。拉伸与挤压是振荡的，波峰来时，上下拉伸，前后挤压；波谷来时，上下挤压，前后拉伸；下一阵波峰到来时，它又会反过来，上下拉伸，前后挤压。

第三点，月亮与引力波产生的潮汐大小不同。月亮产生的潮汐大概是1米，所以潮涨潮落相差2米。而来自黑洞结合的引力波在地球海洋上产生的潮汐不会大于10^-14米，是地球大小的10^-21（单个原子大小的1/10000，刚好比原子核大10倍）。因为潮汐力正比于它所作用的物体的大小（第2章），所以引力波通过潮汐在任何物体产生的变形只有物体大小的10^-12。这意味着，到达地球时，引力波的强度是10^-21。

引力波为什么这样弱呢？因为结合的黑洞离得太远了。引力波的强度与光波一样，随传播距离的增加而衰减。当波还在黑洞附近时，它们的强度大概为1，就是说，物体有多大，它就把它拉伸或压缩多少，在这么强的作用下，人是会丧命的。然而，到达地球时，引力波的强度减小到约（1/30黑洞周长）/（波经过的距离）。^[320]对一个10亿光年远、10个太阳那么重的黑洞来说，引力波强度为（1/30）×（180千米的黑洞周长）/（到地球的10亿光年）≈10^-21。于是，它使地球海洋发生的形变为10^-21×（10⁷米的地球大小）=10^-14米，正好是原子核直径的10倍。

想在地球汹涌的海洋上测量这么微小的潮汐是完全没有希望的。不过，通过周密设计的实验室仪器来测量引力波的潮汐力，还是有希望的——那就是引力波探测器。

棒

约瑟夫·韦伯（Joseph Weber）第一个充满远见地认识到，测量引力波并不是完全没有希望。1940年，韦伯带着工程学士学位到美国海军学院读研究生，二战时在勒星顿号航空母舰上服役，舰在珊瑚海战役沉没后，他成了690号潜艇的指挥官。1943年攻占意大利时，他率领小罗斯福（Theodore Roosevelt, Jr.）准将和1900名突击队员登岸。战后，他是美国海军舰船局电子对抗部的领导。他在无线电和雷达技术方面的造诣是出了名的，所以，1948年马里兰大学请他去担任电子工程学教授，他同意了——成为一名只有大学学士学位的29岁的正教授。

在马里兰大学讲电子工程的同时，韦伯也在准备改行：在天主教大学跟赫兹菲尔德（Karl Herzfeld）学习，成了物理学博士。这位赫兹菲尔德也曾是惠勒的博士导师。韦伯从他那儿学到了很多关于原子、分子和辐射的物理学，从而在1951年发现激光产生的新机制，但他没有条件用实验来证明他的思想。在韦伯准备发表他的思想时，^[321]另有两个小组——一个在哥伦比亚大学，由汤斯领导；一个在莫斯科，由巴索夫（Nikolai Gennadievich Basov）和普罗哈洛夫（Aleksandr Michailovich Prokharov）领导——独立发现了另一种新机制，而且他们接着就发现了激光。^[322]尽管韦伯关于这个机制的论文最先发表，但他几乎什么荣誉也没得到；诺贝尔奖和专利都给了哥伦比亚和莫斯科的科学家。^[323]韦伯很失望，但他与汤斯和巴索夫仍然很友好。他又去找新的研究方向。

韦伯先找到了惠勒的研究小组，工作了一年，成为一名广义相对论专家，跟惠勒一起研究广义相对论对引力波性质的预言。1957年，他又找到了新方向，开始建造世界上第一台寻找和监测引力波的仪器。

从1957年下半年开始，到1959年初，韦伯想尽了他能想到的各种引力波探测方案。这还只是在纸上的脑力训练，没做实验。他的想法写满了4本300页的笔记，包括可能的探测器设计和每一设计预想步骤的计算。一个个想法都因为没有希望而被他扔到一边。但有几个还有希望，韦伯最后选择了一根圆柱形铝棒，长约2米，直径0.5米，重1吨，侧面指向到来的引力波（图10.4下）。^[324]

引力波因为潮汐力的振荡，将交错挤压和拉伸铝棒的两端。铝棒两端具有相对于中心向里和向外振动的自然振动模式，能与振荡的潮汐力发生共振。这种自然振动模式就像铃铛、音叉或者酒瓶的声音一样，有非常确定的频率，与这些自然频率相应的声波能使这些物体产生共鸣；同样，与棒的自然频率相应的振荡潮汐力也能引起棒的共振。于是，以这种棒作为引力波探测器，应该将棒的大小调整到使它具有与到来的引力波相应的自然频率。

图10.4韦伯在介绍绕着铝棒中央贴上去的压电性晶片（约1973年）。引力波驱动铝棒两端振动，振动将内外挤压这些晶片，从而产生可以用电学方法检测的电压。[James P.Blair摄，国家地理学会提供。]

频率该是多少呢？1959年韦伯开始他的计划时，相信黑洞的人很少（第6章），相信者也只认识很少一点儿黑洞性质。那时还没人想到黑洞会碰撞、结合并发射记录它们碰撞历史的时空曲率波，也没人能就其他的引力波源提出有多大希望的指导。

所以，韦伯是从黑暗中摸索起步的。他惟一的指南是粗略（却是正确的）知道引力波的频率大概低于10000赫兹（每秒转10000周）——那是物体以光速绕最紧致的恒星，即接近临界周长的恒星运动的轨道频率。^[325]于是，韦伯设计了他能做到的最好探测器，让它们的共振频率尽可能都落在10000赫兹以下，希望宇宙也能提供具有他所选择的频率的波。很幸运，他的铝棒的共振频率大约是1000赫兹（每秒振荡1000周），后来发现来自结合黑洞的某些波正好就在这样的频率上振荡。某些来自超新星爆炸和结成的中子星对的引力波，也是这种频率。

韦伯计划里最困难的地方在于发明一个用来监测铝棒振动的传感器。他料想，波产生的振动应该很小，小于一个原子核的直径（但在20世纪60年代，他不知道那到底是多小。据最近的估计，它只有10^-21×（2米棒长）≈10^-21米，或者说，只有原子核直径的百万分之一）。对五六十年代的大多数物理学家来说，即使原子核直径的十分之一也是不太可能测量的。但韦伯不这样看，他发明了能胜任的传感器。

韦伯传感器的基础是压电效应：某些类型的材料（特定的晶体或陶瓷）在受轻微挤压时会在两端产生电压。韦伯本想用这类材料来做他的棒，但材料太贵，他只好求其次：用铝做棒，然后绕着棒的中央贴上一些压电性晶体片（图10.4）。棒振动时，表面将挤压或拉伸晶片，每块晶片都产生一个振荡电压。韦伯用电路将晶片一块块串联起来，于是微弱的振荡电压将叠加在一起，即使棒的振动只有原子核直径的十分之一，这样累积的电压也足以用电学方法检测出来。

20世纪60年代初，韦伯还是世界上惟一一个寻找引力波的实验物理学家。带着激光竞争的痛苦回味，他喜欢这种孤独。然而，在70年代初，他那令人感动的敏锐力和他实际可能检测到了的引力波证据（现在想来，我相信他没有检测到），吸引了几十位实验家；80年代，已经有100多位有才能的实验家投身进来，为实现引力波的天文学与他并肩战斗。^[326]

我第一次见韦伯是在法国阿尔卑斯山勃朗峰对面的山坡上，那是1963年的夏天，他着手探索引力波已经4年了。那时我还是刚开始研究相对论的研究生，和来自世界各地的其他35名学生一起到阿尔卑斯山来参加紧张的两个月的爱因斯坦广义相对论引力定律的暑期讲习班。^[327]老师都是世界上最伟大的专家——惠勒、彭罗斯、米斯纳、德维特（Bryce Dewitt）、韦伯等——我们在课堂上听他们讲，私下里与他们交谈。南山的雪闪着耀眼的光芒，勃朗峰直插我们头上的天空；在我们周围，牛群带着铃响在绿油油的牧场上吃草，山下离学校几百米的地方，是美丽如画的莱苏什的村庄。

在这迷人的地方，韦伯讲引力波和他的探测计划，也令我入迷了。课后，我与韦伯谈物理、谈生活，也谈登山。逐渐发现，他和我个性相投。我们都喜欢独处，不喜欢紧张的竞争和激烈的思想讨论。我们更喜欢自己考虑问题，偶尔从朋友那儿听一些建议和想法，但又不让想赶在我们前头获得认识和发现的人从我们身边超过去。

接下来的10年里，黑洞研究热起来了，进入了它的黄金年代（第7章）。我开始感到黑洞研究并不令人喜欢——它太紧张、太激烈、太混乱。于是我忙着找别的自由空间多一些的研究领域，那样我在投入大部分精力后，还可以有点儿时间来研究黑洞或别的事情。在韦伯激发下，我选择了引力波。

我同韦伯的看法一样，引力波的研究还很幼稚，但它有光明的未来。在它萌芽时走进这个领域，我能为帮助它成长而快乐，能为后来的建设者奠定一点基础，而且用不着别人在我耳边唠叨，因为大多数其他相对论理论家那时都聚集到黑洞去了。

在韦伯看来，需要的基础在于实验，也就是，探测器的设计、建造和不断的改进。在我看来，基础在于理论。我们应该努力去认识，爱因斯坦的广义相对论定律关于引力波如何产生、如何在离开时对波源反作用，如何传播，都说了些什么；我们还应该判断，哪类天体会产生宇宙间最强的引力波，有多强，以多大频率振荡；我们还应该发明一些数学工具来解开这些天体产生的交响曲背后的秘密，这样，当韦伯等人最终探测到引力波时，理论和实验才能进行对比。

1969年，应泽尔多维奇的邀请，我在莫斯科过了6个星期。泽尔多维奇向我和其他一些人讲了他的一大堆新想法（第7章、第12章）。一天，他抽时间开车送我去莫斯科大学，把我介绍给一位年轻的实验物理学家布拉金斯基（Vladimjr Braginsky），他在韦伯激发下发展引力波探测技术已经好几年了，是继韦伯之后最先进入这个领域的实验家。他也做其他有趣的实验，例如，寻找夸克（质子和中子的基本构成物质），检验爱因斯坦关于所有物体（不论它的组成如何）在引力场中以相同加速度下落的论断（这是爱因斯坦将引力描述为时空曲率的基础）。

布拉金斯基给我留下了很深的印象。他机敏而深刻，对物理学有非常好的感觉；他热情而直率，很容易同他谈政治和科学。我们很快成了好朋友，也学会了尊重彼此的世界观。对我这样的美国自由民主党人来说，个人的自由是高于一切的，政府没有权力叫人怎么生活。对布拉金斯基这样的非教条共产主义者来说，个人对社会的责任才是高于一切的。

左：1973年9月，韦伯、索恩和Tony Tyson在波兰华沙的一次引力辐射会议上。右：1984年10月，布拉金斯基和索恩在加利福尼亚帕萨迪纳。[左，Marek Holzman, Andrzej Trautman提供；右，Valentin N.Rudenko提供。]

布拉金斯基具有别人没有的远见。在我们1969年见面时，以及后来在1971年和1972年再见时，他都警告我，寻找引力波的棒存在着一个根本的最终极限。^[328]他告诉我，那个极限来自量子力学。尽管我们一般认为量子力学只对电子、原子和分子那样的小事物发生作用，但是，如果对1吨棒的振动测量足够精确，我们会发现那些振动也有量子力学行为，而且这些行为最终会给引力波的探测带来问题。布拉金斯基很相信这一点，因为他计算过韦伯的压电性晶体和其他几类可能用于棒的振动测量的传感器的最终行为。

我不明白布拉金斯基在说什么。我不懂他的理由，不懂他的计算，也不懂它的重要性，所以没太注意。他向我讲的其他事情似乎要重要得多：我从他那儿学会了如何考虑实验，如何设计实验装置，如何预测影响仪器的噪声，如何消除噪声使仪器正常运行——而布拉金斯基从我这儿学的是，如何认识爱因斯坦的引力定律，如何确认那些预言。我们很快结成一个小组，每个人都把自己的专业带进我们共同的事业。在接下来的20年里，我们将得到巨大的快乐，也有一些发现。

20世纪70年代初期和中期，我和布拉金斯基每年都见面，在莫斯科、帕萨迪纳、哥本哈根、罗马或别的什么地方，他每年都警告我量子力学会给引力波探测器带来麻烦，而我每次都没听明白。他的警告有些乱，因为他自己也没完全明白发生了什么事情。然而到1976年，斯坦福大学的吉法德（RobinGiffard）在布拉金斯基后也独立提出这样的警告，而且说得更清楚，我才恍然大悟。我终于意识到问题的严重：棒探测器的最终灵敏度严格受测不准原理的限制。^[329]

测不准原理是量子力学的一个基本特性。它说的是，如果你想高度精确地测量一个物体的位置，那么在测量过程中，你必然会对物体有一种反作用，从而以一种随机的不可预料的方式干扰物体的速度。位置测量越精确，物体速度受到的不可预料干扰就越强烈。不论仪器设计得多么巧妙，你都不可能超越这种固有的不确定性（见卡片10.2）。

卡片10.2

测不准原理与波粒二象性

测不准原理与波粒二象性（卡片4.1）——也就是粒子有时像波、有时像粒子的行为趋向——是密切相关的。

假如你在测量一个粒子（或者别的物体，如棒的端点）的位置，确定它在某个误差区间，那么，不论粒子的波在测量前像什么，在测量中，测量仪器都会对它产生反作用，从而将它约束在误差区间内。于是，得到的波形有点儿像下面的样子：

这样的约束波包含了从误差区间本身大小（图上标极大）到波的两端所在小区域的大小（图上标极小）的不同波长。更具体地说，受约束的波可以通过下面这些波长从极大到极小的波动之和或叠加来构成：

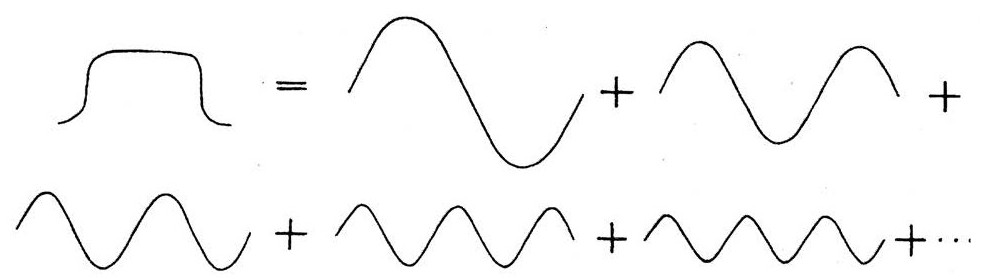
现在，想象波振荡的波长更短，粒子的能量更大，从而粒子的速度也更大。因为测量为波限定了一个波长范围，所以粒子的能量和速度也一定落在一个相应范围内；换句话说，它的能量和速度是不确定的。

概括地讲，测量将粒子的波约束在一定误差区间内（上面第一个图），使波由一定范围内的波长组成（第二个图），而波长的范围对应一个能量和速度的范围，从而速度是不确定的。不论你费多大气力，你在测量粒子的位置时，都免不了产生这种速度的不确定性。而且，更深入的论证表明，位置测量越精确，即误差区间越小，波长和速度的范围就越大，这样，粒子速度的不确定性也就越大。

测不准原理不仅决定电子、原子和分子等微观事物的测量，也影响宏观事物的测量。但是，由于大物体有大惯性，测量的反作用只能产生很轻微的速度扰动（速度受到的干扰与物体质量成反比）。

在引力波探测器问题上，测不准原理说的是，传感器对振动棒两端的位置测量越精确，测量对棒产生的随机反作用就越强大。

对于不精确的传感器，测量的反作用可能很小而无关紧要，但如果传感器不精确，你从哪儿知道棒的振动幅度呢？当然也就更不可能监测到微弱的引力波。

对于极端精确的传感器，反作用可能很大，能强烈改变棒的振动。这些巨大的未知的变化，将淹没你想探测的任何引力波。

在这两个极端之间，存在一个理想的传感器精度：它既不因为太低而令你一无所获，也不因为太高而出现不可知的强大反作用。在这样一个现在称为布拉金斯基标准量子极限的理想精度下，测量产生的反作用的效应几乎与传感器产生的误差一样小。没有传感器能比这个标准量子极限更精确地监测棒的振动。那么极限是多大呢？对2米长、1吨重的棒来说，大约比一个原子核小100000倍。

20世纪60年代，谁也没有认真考虑过需要这么精确的测量，因为没人清楚地知道来自黑洞和其他天体的引力波会有多么微弱。不过到70年代初，在韦伯实验计划激励下，我和其他理论家已经指出了最强引力波可能具有的强度，大约是10^-21，^[330]这意味着波在2米棒产生的振动幅度只有10^-21×（2米），约一个原子核直径的百万分之一。如果这些估计是正确的（我们也知道那是很不确定的），那么引力波信号比布拉金斯基标准量子极限小10倍，从而不可能用棒和任何已知类型的传感器来监测。

这实在令人忧虑，但并不是一切都完了。布拉金斯基深刻的直觉告诉他，如果实验者有特别机灵的办法，还是可能超越他的标准极限。他指出，这需要用一种新办法来设计传感器，使它不可避免的未知的反作用不会掩盖引力波对棒的影响。布拉金斯基称这样的传感器为量子无破坏^[331]传感器。“量子”是由于传感器的反作用来自量子力学定律的要求，“无破坏”说的是传感器的设计避免了反作用对被测物体的破坏，也就是反作用不会破坏引力波对棒的影响。布拉金斯基也没有可行的量子无破坏传感器的设计，但直觉告诉他，这样的传感器应该是可能的。

这一次我很认真地听了布拉金斯基的话。在接下来的两年里，我和我在加州理工学院的小组以及他和他在莫斯科的小组都在断断续续地努力，为的就是设计一台量子无破坏传感器。

1977年秋，我们同时找到了答案——但方法完全不同。^[332]我清晰记得，我当时是多么兴奋。那是某一天在格里西（学院的学生食堂）午餐后，凯维斯（Carlton Caves）和我在激烈讨论中突然想到的。^[333]我还记得，当我得知布拉金斯基、沃罗索夫（Yuri Vorontso V）和哈里利（Farhid Khalili）几乎同时在莫斯科发现了相同的重要思想时，我心中涌起一股辛酸和喜悦的感觉——辛酸是因为我曾满以为自己是新事物的第一个发现者；喜悦是我为布拉金斯基感到骄傲，为能和他同享一个发现而感到高兴。

我们的量子无破坏思想很抽象，它允许很大一类传感器设计超过布拉金斯基的标准量子极限。然而，因为思想抽象，我很难解释。所以，我在这儿只讲一个（不太实用的）量子无破坏传感器的例子。^[334]布拉金斯基称它是频闪传感器。

频闪传感器依赖于棒振动的一个特殊性质：假如棒受到一个尖锐的未知反冲作用，它的振幅将发生改变，但不论振幅怎么变化，经过一个振动周期后，棒的振动端将回到它受反冲时的位置（图10.5中的黑点）。至少在引力波（或其他力）没有同时作用在棒上时是这样的。假如引力波（或其他力）同时在挤压棒，那么一个周期后，棒的位置会发生改变。

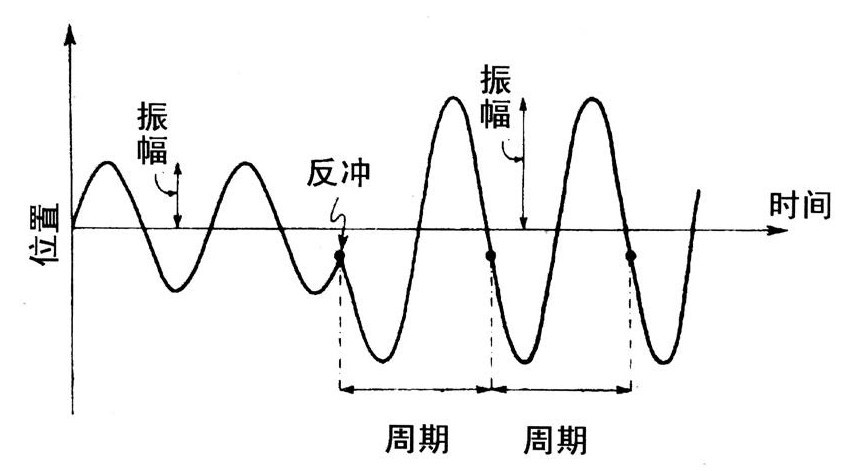
图10.5频闪量子无破坏测量方法的原理。纵向画的是振动棒端点的位置，横向为时间。如果在反冲时刻迅速而高精度地测量一个位置，则传感器将对棒突然产生一个未知的反冲作用，从而以未知方式改变棒的振幅。然而，在一个两个或者若干个周期后，棒端的位置仍然不会改变，还是与反冲时刻的位置一样，而且完全与反冲作用无关

于是，为了探测引力波，应该造一台对棒的振动端进行频闪测量的传感器，也就是，传感器在每个振动周期内很快地测一次棒端的位置。这样的传感器在每次测量时都会对棒产生反冲作用，但这些反冲作用在后续测量时不会改变棒端的位置。如果发现位置变了，那么一定有引力波（或其他力）作用在棒上。

虽然量子无破坏传感器克服了布拉金斯基的标准量子极限，但到20世纪80年代中期，我却对棒探测器的前景感到悲观，恐怕它不会为引力波天文学带来什么结果。我悲观的原因有两个：

第一，尽管韦伯、布拉金斯基以及其他一些人做的探测棒已经达到了20世纪50年代不可想象的灵敏度，但它们只能可信地用来探测强度在10^-17以上的引力波，如果我和其他一些人对到达地球的引力波强度没有估计错的话，这个精度离成功还差10000倍。这本身倒并不严重，因为在20年的时间里，技术的进步常能使仪器的本领提高10000倍。[一个例子是射电望远镜的角分辨率，它从20世纪40年代中期的几十度提高到了20世纪60年代中期的几弧秒（第9章）。另一个例子是X射线天文探测仪的灵敏度，从1958年到1978年，它提高了10¹⁰倍，就是说，平均每8年提高10000倍（第8章）]。然而，棒的进步太慢了，而且没有未来技术和工艺的大胆计划，看来，想在不远的将来实现10000倍的进步，恐怕找不到什么可能的办法。这样，成功只好靠比10^-21的估计更强的波了——这倒真是可能的，不过没人愿意依赖它。

第二，即使棒探测到了引力波，要解释它的交响信号也将遇到巨大的困难，实际上很可能会失败。原因很简单：正如音叉或酒杯只对接近其自然频率的声波产生共振，棒也只对接近它自然频率的引力波才有响应；从技术上说，棒探测器只有一个很窄的带宽（带宽就是它产生响应的频率范围），但引力波的交响信号通常混合着一个范围很宽的频率。于是，为了析取这些波的信息，需要一个由许多棒组成的“木琴”，每一根棒覆盖一个不同的小频率带。这架木琴需要多少棒呢？用那时正在计划和制造的那种棒，需要几千根——这实际上是不可能的。原则上讲，要增大棒的带宽，^[335]用十几根就够了，但那么做所要求的主要技术进步比达到10^-21的灵敏度还高。

尽管在20世纪80年代，我没有公开讲过多少悲观的话，但我自己还是认为那是可悲的，因为我看到了韦伯、布拉金斯基和我其他朋友和同事为探测棒付出的巨大努力，也因为我已经相信，引力辐射有力量在我们的宇宙认识中产生革命。