第4篇　围攻篇

第19章　大规模演绎的武器

事实上，我更愿意把弦论称为一个“模型”，甚至仅是一种基于直觉的想法，而不是一个“理论”。毕竟一种理论应该同时能指导人们，如何运用它来确认人们试图表述的事物，就我们的情况来说，那就是基本粒子。人们至少原则上应该能构想出计算这些粒子性质的原理，同时阐明如何对这些粒子作出新的预言。试想我给你一把椅子，同时又跟你解释说，椅子还没有腿，坐板、靠背和扶手也许一会儿会送过来；不论我真正给了你什么，我还能称其为椅子吗？

——赫拉德·特霍夫特

就全息原理本身而言，它并不足以赢得这场战争。它太不精确了，它缺少一个坚实的数学基础。人们以怀疑的方式作出反应：宇宙是一个全息图？这听起来像科幻小说。小说中未来的物理学家史蒂夫穿越到了“另一边”，而皇帝和伯爵却看着他慢慢死去？听起来像唯灵论的呓语。

一个本来可能多年默默无闻的另类想法突然被人所接受，并让天平倾斜到了它那一边，到底是什么缘故呢？在物理学中，它常常悄悄地就发生了，毫无征兆。一个重要的、戏剧性的事件突然间抓住了许多物理学家的兴趣，而且在一个短时间内，怪异、荒诞、不可想象的东西变成了寻常的东西。

有时候它是一个实验结果。爱因斯坦关于光的粒子理论起初并不太被认可，大部分物理学家相信某种新的观点会拯救波动说。但是在1923年，阿瑟·康普顿（Arthur Compton）从碳原子对X射线散射的角度和能量清楚地证明了，这是粒子在碰撞。从爱因斯坦第一次提出这个想法到康普顿的实验花了18年时间，但是，就在几个月时间内，对于光的粒子理论的抗拒都消失了。

当一个数学结果出乎意料的时候，它极有可能是一场灾难。（基本粒子物理的）标准模型的基础建立于20世纪60年代中期，但是当时人们对此模型颇有质疑，认为其数学基础是不自洽的，其中有些还来自于该理论的创立者。在1971年，一个年轻的、名不见经传的学生完成了一个极其复杂且精妙的计算并宣布专家们错了。在极短的时间内，标准模型正式成为标准的，而这个不知名的学生，赫拉德·特霍夫特，横空出世，成为一颗物理世界最闪亮的明星。

另一个关于数学如何让天平向一个“怪异”想法倾斜的例子就是史蒂芬·霍金关于黑洞温度的计算。早期人们对贝肯斯坦关于黑洞具有熵的观点持怀疑态度，甚至是嘲讽，但是霍金并不如此。现在看来，贝肯斯坦的论证极其聪明，但是那时它们显得太模糊太粗略，很难使人信服。正是霍金那难度极大的积分技术，才使得黑洞的范式从冷的死星变成了一个带有内部温度的发热物体。

我所描述的这些关键性的时刻有着一些共同的特征。首先，他们都是出乎意料的。一个完全没有想到的结果，不论是实验上还是数学上，都会吸引到大量的关注。第二，对于一个数学结果，如果技术性越强、精确性越高、非直觉性越强、难度越大，就越容易使人感到震惊，从而这种新的思维方式的价值便会得到承认。部分原因在于复杂的计算很多时候都可能出错。能在这种潜在危险中存活下来的理论，不会被人弃之不顾。特霍夫特和霍金的计算都具备这个特质。

第三，当新的想法提供了许多更加简单的方法去做的时候，范式就变化了。物理学家们一直在寻找新的想法，并立刻着手为他们各自的领域创造机会。

黑洞互补性原理和全息原理当然是出人意料的，甚至是震惊的，但是就它们本身而言并没有具备其他两种特质，至少那时还没有。在1994年，一个关于全息原理的实验验证和数学证明似乎都是不可能的。实际上，它们离突破口已经很近了，比任何人想象的都要近。两年后，一个精确的数学理论慢慢成形。而10年之后的今天，我们可能也已经接近实验上的验证了^[159]。正是弦论使得它们成为可能。

在讲一些弦论的具体东西之前，先做一个总体的描述。没有人能确定弦论是否是我们世界的正确理论，在以后的很多年里可能还是无法确定。但是考虑到我们这里的目的，这并不是最重要的。我们有很多论据，可以证明弦论是一个关于某个世界的自洽的数学理论。弦论基于量子力学的原理，它描述了一个与我们宇宙类似的基本粒子体系；它不像其他理论（例如量子场论），弦论中所有物质都由引力传递相互作用。最重要的，弦论包含了黑洞。

如果我们不知道它是否是正确理论，我们怎么用弦论来证明呢？出于某种目的，这不成问题。我们先把弦论看成某个世界的模型，然后通过计算或者数学上的证明，看信息在那个世界中是否丢失在黑洞了。

先假设我们发现在这个数学模型中信息没有丢失。只要我们发现信息没有丢失，那么我们可以更仔细地研究，并找到霍金哪里错了。我们可以了解到黑洞互补性原理和全息原理在弦论中是否正确。如果确是如此，那么这证明的并不是弦论是正确的，而是霍金错了，因为他宣称在任意自洽的世界中，黑洞必定都会毁灭信息。

我将把关于弦论的诠释减到最小。如果你想知道更多的细节，那么你可以在许多书中找到，包括我早期的书《宇宙概貌》，布莱·恩格林（Brian Greene）的《宇宙的琴弦》，以及莉萨·兰德尔（Lisa Randall）的《偏见的交流》。弦论是一个意外的发现。开始的时候，它与黑洞或者量子引力支配的遥远的普朗克世界并没有关系。它只是与更为普通的强子领域相关。强子这个词不是一个每天都能碰到的平常术语，但是强子是自然界中最普通也是研究得最多的粒子之一。它们包括质子和中子，即组成原子核的粒子，以及一些叫作介子和被随意命名为胶子的近亲。在它们的鼎盛时期，强子是基本粒子物理中的前沿课题，但今天它们常常与核物理那些略显过时的课题相关。然而，在第23章中，我们将看到一个闭合圆圈的想法让强子成为物理学的“王者归来”。

初等还是基本^[160]

有一个关于两个犹太女士的老故事。一次，她们在布鲁克林的街角相遇，其中一个对另一个说：“你一定听说过我儿子现在是医生吧。顺便问一句，你儿子后来怎么样了？他那时学算术很吃力哦。”另一个女士回答说：“啊，我的孩子现在是一名哈佛的物理教授，研究基本粒子。”第一个女士深表同情地说：“哦，我的天哪，听到这个我感到很难过，他还没毕业就去学高等粒子物理啊?”

我们所说的基本粒子到底是指什么，与之相对的又是什么？最简单的答案就是一个不能再分拆成更小部分的极其微小和简单的粒子。与之相对的不是高等粒子，而是复合粒子——一个由更小更简单的部分组成的粒子。

还原主义是一种把事物分解成各种组分来理解的科学哲学。到现在，这种想法工作得很好。分子被看成是由原子组成的；接着，原子是一些带负电的电子围绕带正电的原子核绕转；原子核则被看成是一团核子；最终，每一个核子是由3个夸克组成的。今天所有的物理学家都认为分子、原子、原子核和核子都是复合的。

但是在过去某个时候，这些客体都曾被认为是基本的。实际上，原子这个词来自于古希腊，意为不可再分的东西，已经被使用了约2500年。后来，欧内斯特·卢瑟福发现了原子核，它如此之小，以致可以看做一个简单的点。最终，这个被一代人称为基本的东西在他们的后代看来是复合的。

所有这些会导致一个问题：我们怎么确定，至少目前，某种粒子是基本的还是复合的。这里有一种解决的方案：将两颗该粒子极为猛烈地相撞，然后看是否有东西出来。如果有东西出来，那么它之前必定在原来粒子的内部。实际上，当两个非常快的电子以很大能量碰撞，各种粒子喷涌而出，特别是光子、电子和正电子^[161]。如果碰撞能量非常高，质子和中子以及它们的反粒子^[162]都会出现。更有甚者，有时一整个原子也可能出现。这就意味着电子是由原子构成的吗？显然不是。用大量的能量去粉碎东西可能会对了解粒子的特性有帮助，但是所跑出来的各种粒子并不总是一个好提示，来告诉我们粒子由什么构成。

这里有一个更好的办法来判断某样东西是不是由部分组成的。我们从一个复合的东西开始——一块石头、一个篮球或者是一块做比萨饼的面团。对于这些东西我们有很多可以做，例如把它挤压到一个更小的体积中，使其变形成为一个新的形状，或者让它开始绕一个轴旋转。挤压、弯曲或者旋转一个物体都需要能量。例如，一个转动的篮球有动能；它转得越快，能量就越大。而且因为能量就是质量，飞速旋转的球具有更大的质量。一个测量转动速率的观测量，一个结合了球的旋转快慢、尺寸以及质量的量，被称为角动量。随着球的角动量越来越大，它的能量也越来越大。下图就说明了一个转动的篮球其能量增加的方式。

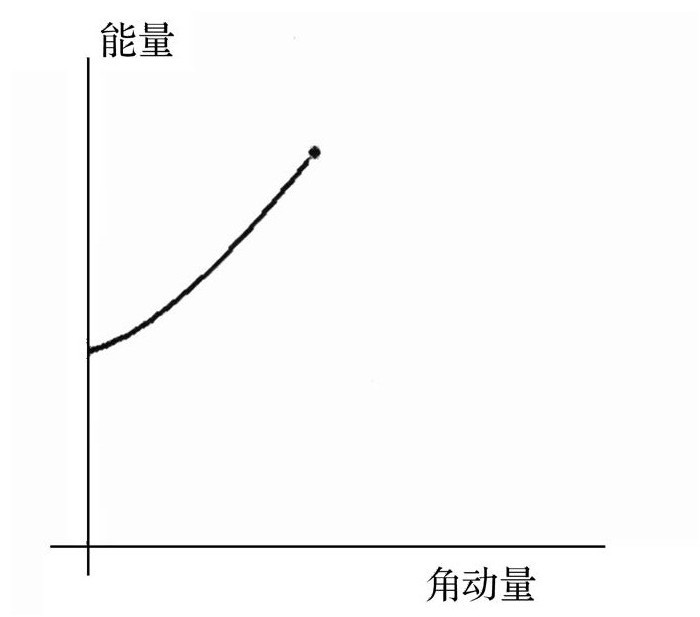
旋转的篮球

但是为什么这条曲线突然终止了呢？这个答案很容易理解。构成这个球的物质（皮或橡胶）只能经受得住这一点压力。从某种角度上来说，这球是被离心力撕裂了。

现在想象一个比空间点还要小的粒子。你如何使一个数学上的点绕着一根轴旋转？那样做将意味着什么？或者说对于这样的物质，改变它的形状意味着什么？如果物体具有旋转的能力或者外形有振荡的能力，这就标志着它是由一些更小的成分组成的，而这些成分彼此可以相对移动。

分子、原子以及原子核可以自己绕着自己旋转，但是对于这些微观的球，量子力学将起关键的作用。与所有其他振荡系统一样，能量和角动量只能以离散的方式增加。一个旋转的盒子其能量并不是逐渐增加的，它更像是突然上了一个台阶。这幅关于能量和角动量的图是一系列分立的点^[163]。除了每一步都是离散的之外，这幅图看起来与篮球那幅图很相似，包括最后突然的终止。就像篮球一样，原子核只能承受住这么多的离心力，再大它就会飞散开去。

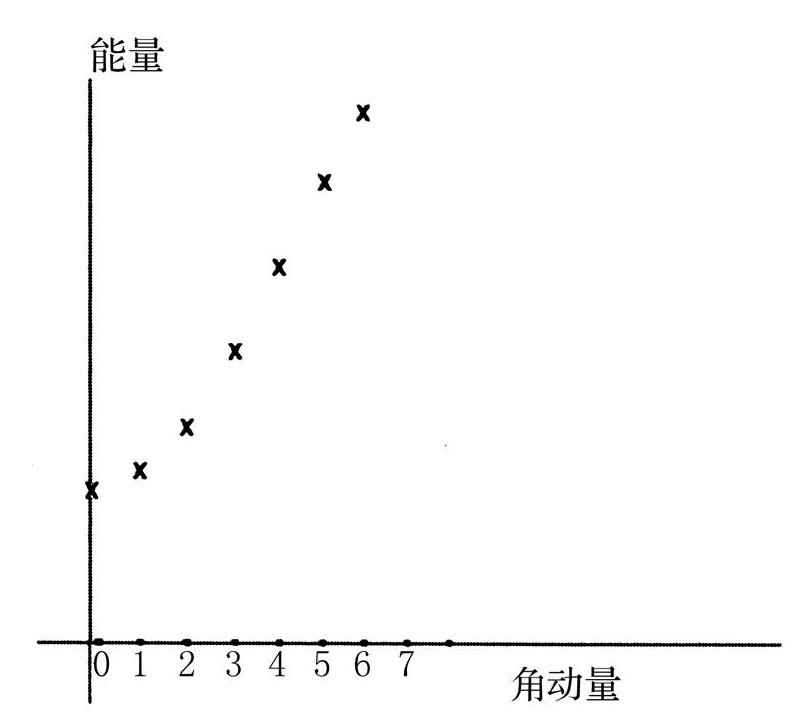
旋转的原子核

那么电子呢？我们能够使它们自己绕自己旋转吗？人们考虑了好多年，但是没有人成功地给一个电子外加上角动量。后面我们将回到电子，但是让我们先转到强子：质子、中子、介子和胶子球。

质子和中子非常类似。它们的质量几乎相同，而且把它们结合成原子核的力也几乎是相同的。唯一重要的不同就是质子带有少量的正电荷，而中子如它的名字一样是电中性的。一个中子就好比是一个去除了电荷的质子。正是这种相似性使物理学家们把它们统称为一个客体：核子。质子是带正电的核子，而中子则是中性的核子。

在核物理研究的早期，核子被认为是一种基本粒子，虽然它的质量约为电子的2000倍。但是核子并不像电子那么简单。随着核物理的发展，一个是原子的十万分之一的物体也不再显得非常小了。虽然电子还是占据了空间中的一个点，至少我们现在可以这么说，核子内部被证实有更加复杂的结构。核子更像原子核和分子而不是电子。质子和中子是许多更小的物体的聚合物。我们知道那是因为我们可以使它们旋转和振荡，然后我们可以改变它们的形状。

就跟篮球或者原子核一样，我们可以画一幅图来表示出核子的自旋，横轴表示角动量，竖轴表示能量。40多年前当人们第一次画出这幅图时，发现其模式显得出人意料的简单：这一系列点几乎成一条直线。更令人吃惊的是，它似乎没有终点。

这类关于核子内部结构的示意图给我们提供了很多线索。对那些知道如何读取隐藏信息的人来说，这两个值得注意的特征有重大的意义。核子可以绕着一根轴旋转，这意味着它不是一个点粒子；它是由一些相互移动的部分组成。而且这个序列似乎将一直延续下去，而不是突然中止。这意味着核子不会在旋转过快时飞散开去。把各个部分结合在一起的那种力，比原子核内的结合力要大得多。

核子会在它旋转的时候延伸开，但是不像一块旋转的比萨面团变成一个二维的圆盘。这并不奇怪。

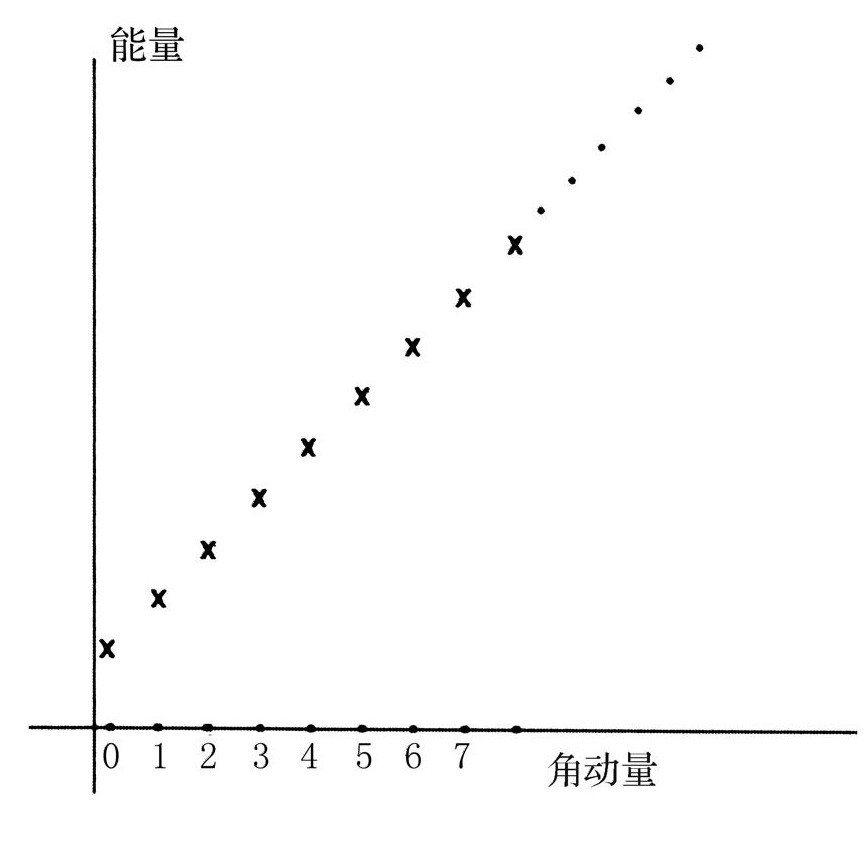
旋转的核子

核子延伸的样式是一条直线，这意味着这个核子延展成了一个长的、细的、具有弹性的、像弦一样的东西。

半个世纪的实验已经确认了核子是一些受到能量激发后可以延展、旋转和振荡的有弹性的弦。事实上，所有的强子自旋后都可以变成长的像弦一样的东西。很显然，它们都是由同样的、有黏性的、纤细的、可以拉伸的东西组成，就像那些极为黏人的甩也甩不掉的泡泡糖。理查德·费曼用部分子来表示这种核子的成分，但是默里·盖尔曼另起的两个名字——夸克和胶子——沿用至今。胶子指的是一种组成长弦并阻止夸克分离的黏性很强的物质。

介子是最简单的强子。人们已经发现了许多不同种类的介子，但是它们有着同样的结构：一个夸克和一个反夸克，中间由一根黏性很强的弦相连接。

一个介子可以像弹簧一样振荡，像啦啦队队长的领操棍一样绕轴旋转，或者以各种方式弯曲折叠。介子是典型的开弦，即它们有终端。在这个方面，它们不像橡皮筋，我们称橡皮筋为闭弦。

核子有三个夸克，每一个都连着一根弦，而这三根弦在中心结合，就像高卓人的波洛领带^[164]。它们也可以旋转和振荡。

强子快速的旋转和振荡给弦增加了能量，拉长了它，也增加了质量^[165]。

还存在着另一种强子：一种“无夸克”粒子，它们是一些闭合成圈的弦。强子物理学称它们为胶子球，但是对于一个弦论学家而言，它们仅是闭弦。

夸克似乎不是由更小的粒子构成的。它们像电子一样，因为太小所以无法检测到其尺寸。但是结合夸克的弦却是由其他物体组成的，而且这些物体不是夸克。这些结合成弦的黏性粒子被称为胶子。

从某种角度来说，胶子是弦上非常小的部分。虽然它们极其微小，但是它们似乎有两个“端点”，一正一负，看起来就像是些小磁铁^[166]。

胶子

关于夸克和胶子的数学理论被称为量子色动力学（QCD），一个听起来更像是与彩色摄影相关的东西，而与基本粒子没什么关系。大家马上就会对这个术语有清晰的认识。

根据QCD的数学规则，一个胶子自己不能单独存在。数学上要求其正负两个端点都与其他胶子或者夸克相连接：每一个正端点必须与另一个胶子的负端点或者夸克相连；每一个负端点则必须跟另一个胶子的正端点或者反夸克相连。最后，3个正的或者负的端点可以结合在一起。根据这些规则，核子、介子和胶子球可以被轻易地组合起来。

如果介子中的夸克受到一个很强的力，它将会发生什么呢？夸克将开始迅速地远离反夸克。如果它与一个原子内部的电子相类似，那么它将会飞离出去并且逃逸掉，但是这里发生的却完全不同。当它与它的另一半开始分离时，胶子间会形成一条缝，就像一根橡皮筋被拉断时它里面分子的状况。然而，胶子们会自我复制，制造出更多胶子来填充这条裂缝，以避免断裂。夸克和反夸克之间形成的弦通过这种方式阻止了夸克的逃逸。下面一系列的图描绘的就是一个介子中的高速夸克，试图逃离反夸克伙伴的过程。最后，这个夸克将耗尽能量而转向朝反夸克运动。核子内部的高速夸克也会发生同样的事情。

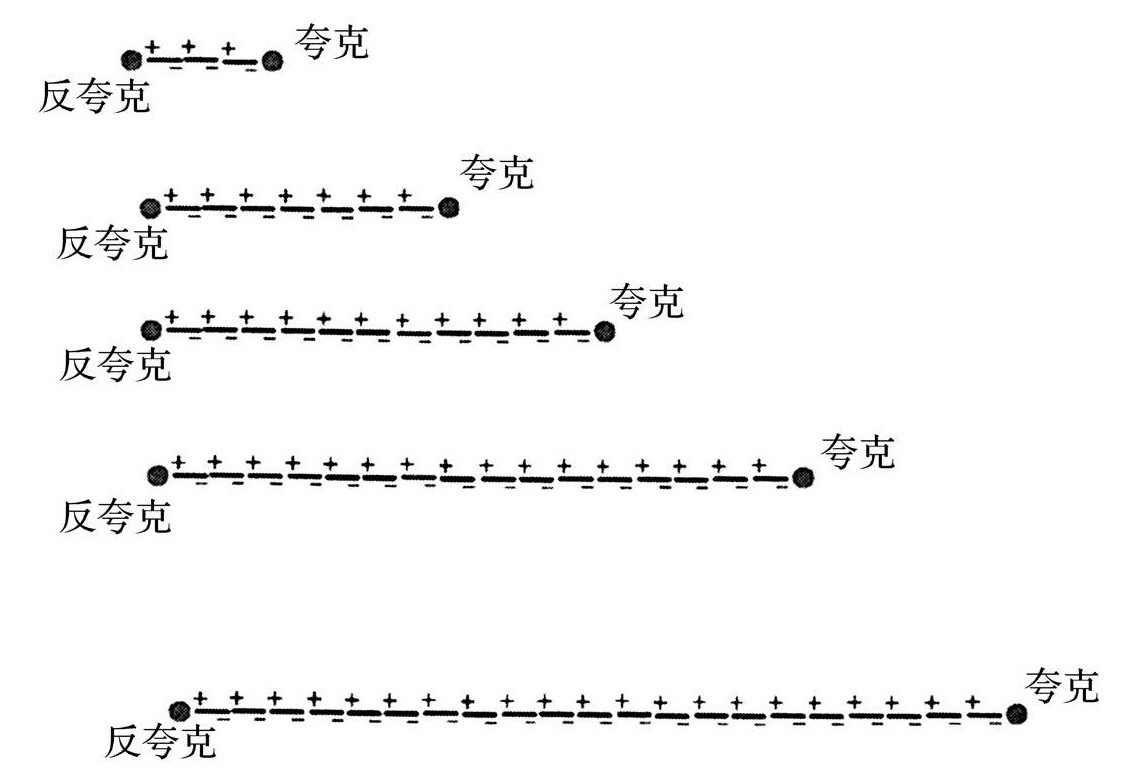
核子、介子和胶子球的弦论并不是一项无所事事的探索。它经过了多年的验证，现在已经被认为是强子标准理论中的一部分了。令人困惑的是我们是否应该认为弦论是量子色动力学的一个结论，换句话说就是，弦是由更加基本的胶子所组成的长链，还是胶子就是弦上的一些小片段？这两者很可能都是对的。

夸克似乎与电子一样小，一样基本。它们不能旋转，不能被压缩也不能形变。尽管它们看起来没有什么内部结构，但是它们有一个复杂性的自由度。这看起来似乎有点矛盾。夸克有很多类型，它们带有不同的电荷和质量。是什么导致这些差异的仍是一个谜；这个决定差异的内部机制实在太小以至于无法观测。所以我们把它们叫作基本的，并像植物学家一样给它们起了不同的名字，至少目前是这样。

在第二次世界大战之前，物理学还是以欧洲为中心。物理学家用希腊语来命名粒子。光子、电子、介子、重子、轻子，甚至连强子的名字都是来源于希腊文。但是后来傲慢无礼，有时有点傻乎乎的美国人取得主导地位，命名这件事就变得随意了。夸克是来自詹姆斯·乔伊斯（James Joyce）的《芬尼根彻夜祭》中一个没有意义的单词^[167]，从文学的观点上来看，这是种退步。人们用“味”这个并不恰当的单个字的词，来描述不同夸克类型之间的区别。我们可能会说巧克力夸克、草莓夸克、香草夸克、开心果夸克、樱桃夸克和薄荷味的巧克力片夸克，但是我们不那么说。夸克的六种味是上、下、奇、粲、底和顶。底和顶曾经一度被认为是不雅的，所以有段时间它们被改成了真和美^[168]。

我为何要详述这些味呢？主要目的是想说明，我们对这些构成物质的基石了解甚少，而且基本粒子这个词所对应的工作只是试探性的。但是还有另一个分类方式，它对于量子色动力学很重要。每个夸克——上、下、奇、粲、顶、底——被分为三种颜色：红色、蓝色和绿色。这也正是量子色动力学中“色”字的来源。

现在我们稍停一会儿。一般意义上来说，夸克太小当然不能反射光线。彩色的夸克与巧克力、草莓和香草夸克相比，只能说傻乎乎的程度略微少了一些而已。但是人们需要用名字来叫这些东西；把夸克称作红色、绿色和蓝色，跟把自由主义者叫作蓝色，把保守派叫作红色一样可笑。虽然，与味一样，我们可能不知道夸克颜色的来源，但是颜色在QCD中扮演的角色却要重要得多。

根据QCD，胶子没有味，但是它们的颜色比夸克更复杂。每一个胶子都有一个正极和负极，而且每一极都有一种颜色：红色、绿色和蓝色。胶子有9种类型^[169]，这种说法有一点过于简单，但是基本上还是正确的。

九种胶子

为什么存在三种颜色，而不是两种或四种抑或是其他种数呢？这与颜色的视觉效果依赖于三原色无关。如我前面提到的，颜色标签是任选的，而且与你我所看到的颜色无关。事实上，没有人确切知道为什么是三种；这些神秘的未知的东西告诉我们，离全面了解基本粒子还差得很远。但是从它们结合形成核子和介子的方式，我们可以知道夸克有三种且仅有三种颜色。

我这里要忏悔一下。尽管我已经当了40多年的粒子物理学家，但是我实在不是很喜欢粒子物理。整个东西太混乱了：6种味、3种颜色、许多任意设定数值的常数——这不是简单优雅的东西。那为什么要一直做这个呢？理由（我确信这不仅仅是我个人的看法）是这个极其混乱的理论一定在告诉我们一些自然本质的东西。很难相信无穷小的点粒子，可以有那么多的特性和那么多的结构。从某些未发现的层面上来看，一定有很多更基本的机制支配着这些所谓的基本粒子。对于这些隐藏的机制以及它里面所暗示的自然界基本原理的好奇心，迫使我在粒子物理这片痛苦的沼泽上继续前行。

随着粒子物理的日渐流行，夸克也开始被公众所熟知。但是如果一定要我猜哪种粒子能提供关于隐藏机制的最好的线索，我会将宝押在胶子上面。那黏糊糊的一对正负极会告诉我们什么呢？

在第4章中，我解释了量子场论不仅仅是一堆粒子。还有另外两个要素：传播子和角点。首先我们来看传播子，它的世界线表示一个粒子从时空的一点到另一点的运动。因为胶子有两个极，每一极都标有一种颜色，所以物理学家们通常用双线来表示世界线。要表示某一个具体类型的胶子，我们可以在每条线的边上写上颜色^[170]。

量子场论中最后一个要素就是角点列表。对于我们来说，角点最重要的是它表示了单个胶子一分为二的性质^[171]。模式相当简单：当一个具有两个端点的胶子分裂时，必定会出现两个新的端点。根据QCD的数学规则，新端点必定具有同样的颜色。下面是两个例子。从下往上看，第一幅图中，一个蓝—红胶子分裂成为蓝—蓝和蓝—红胶子；第二幅图中，一个蓝—红胶子分裂成为蓝—绿和绿—红胶子。角点可以被翻转过来，显示两个胶子是如何结合成为一个胶子的。

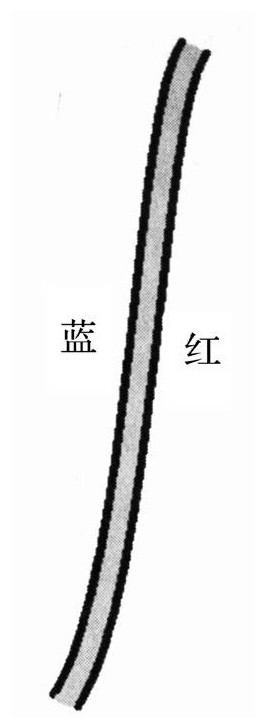
尽管这并不是一目了然的，完全理解它需要花一定的时间，但是胶子有着强烈的倾向，想要黏合在一起并形成长链：正端点链接负端点，红接红，蓝接蓝以及绿接绿。这些链就是结合夸克的弦，而且给了强子类弦的特性。

底层上的弦

在量子引力的研究中，有弹性的弦的想法又一次出现了。然而不一样的是，一切都变小和变快了20个数量级。这些微型的、快速的、能量极高的弦被称为基本弦^[172]。

为了避免后面发生混淆，我再说一遍：弦论在现代物理学中有两种不同的应用。在强子中的应用，那个尺度在常人看起来极其微小，而在现代物理学看来却非常大。强子的三种类型——核子、介子和胶子球——都是类弦的物体，可以用弦论的数学描述，这些都是公认的事实了。那些支撑强子弦理论的实验室实验，可以追溯到半个世纪之前。这种由胶子构成的，连接强子的弦被称为QCD弦。基本弦则是与引力和普朗克尺度附近的物理相关的弦。它让人兴奋而爱辩，在博客上夸夸其谈，还在近期著书论战。

基本弦与一个质子相比就像一个质子与新泽西州相比，要小很多。对于基本弦来说，引力作用是最重要的。

引力在很多方面与电力极为类似。带电粒子间的力学规律被称为库仑定律；引力规律被称为牛顿定律。电力和引力都遵循平方反比律。这意味着力的强度与距离的平方成反比。粒子间的距离增加1倍，其间的力将变为1/4；距离变为3倍，那么力将变为1/9；距离变为4倍，力将变为1/16，等等。两个粒子间的库仑力正比于它们所带的电荷；牛顿引力正比于它们的质量。这些是相似之处，但是它们仍有不同：电力既可以排斥（同性之间），也可以吸引（异性之间），但是引力总是相互吸引的。

一个很重要的相似之处，就是这两种类型的力都能产生波。想象有两个相隔很远的带电粒子，如果突然移动其中一个——假设是远离另一个电荷——那么这两者之间的力会发生什么变化呢？有人可能会认为当第一个粒子移动后作用在第二个粒子上的力将瞬间变化。如果一个作用在遥远的电荷上的力确实是瞬时变化的，没有任何延迟，那么我们可以利用这个效应，给空间中遥远的区域发送瞬时信息。但是瞬时信息破坏了一个自然界中最深刻的原理。根据狭义相对论，没有信息能超光速传递。你不可能用比光传播更短的时间传递一个信息。

实际上，当一个邻近的粒子突然移动时，作用在遥远的粒子上的力并不是瞬间改变的。一个扰动从这个被移动的粒子（以光速）传播出去。只有当扰动到达那个遥远粒子的时候，作用在该粒子上的力才会改变。这个传播出去的扰动类似一个振荡的波。当这个波最终到达时，它摇动了第二个粒子，就像一口池塘中的软木塞，随波荡漾。

如果是引力，情况是类似的。想象有一只巨大的手摇动着太阳。太阳的运动在8分钟内是不会被地球所感知的，这个也就是光在两者间传播的速度。这个“信息”以一种曲率涟漪的方式也叫引力波的方式传递。引力波的传播速度与光速相同。质量对引力波所起的作用，犹如电荷对电磁波一样。

现在让我们再添加一些量子理论的知识。如我们已知道的，振荡的电磁波其能量是以一种不可分割的量子方式出现，这种量子被称为光子。普朗克和爱因斯坦都认为振荡的能量是以离散的单元出现，除非我们弄错了，不然这些相同的论证是可以运用在引力波上面。引力场的量子被称为引力子。

我应该在这里说明，与光子不同的是，引力子的存在只是一个实验无法检测的猜想，尽管大部分物理学家们认为它基于坚实的原理，不算是一个猜想。即便这样，对于那些已经思考过它的物理学家来说，引力子背后的逻辑是令人信服的。

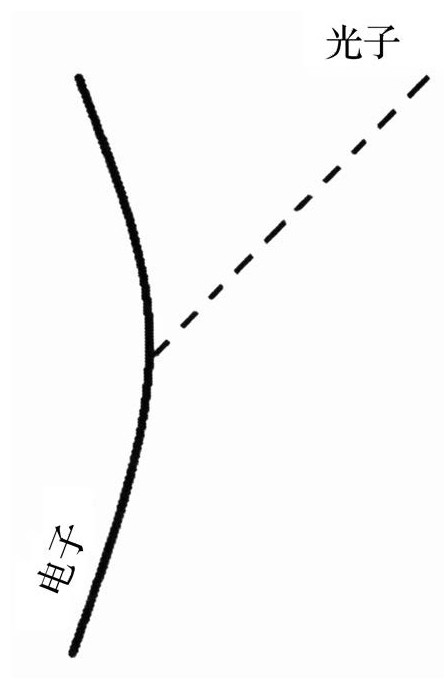
光子发射角点

光子和引力子间的相似性导致了一些有趣的问题。在量子场论中，电磁辐射用一个角点图解释，图中一个诸如电子那样的带电粒子，发射一个光子。

人们很自然地想到，当粒子发射引力子时会产生引力波。因为任何东西都受引力的作用，所有粒子必定有能力发射引力子。

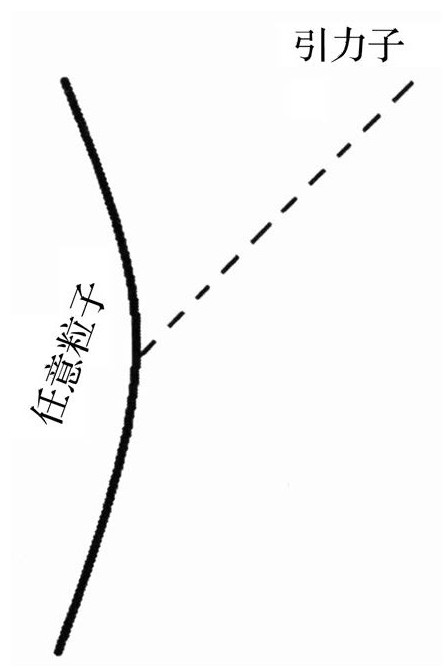
引力子发射角点

甚至一个引力子也可以发射一个引力子。

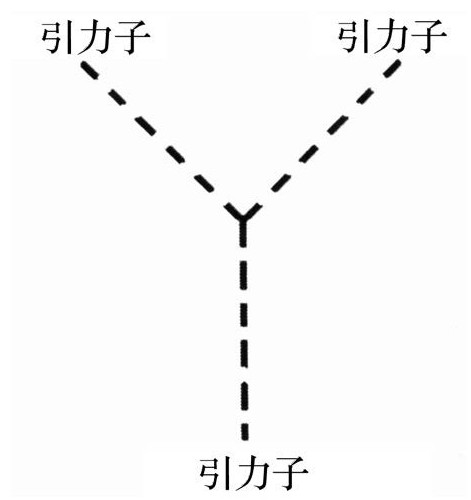
不幸的是，包含引力子的费曼图会导致数学上的灾难。近半个世纪以来，理论物理学家们尝试了解引力子的量子场论，但是不断的失败使我们相信，这是一件愚蠢的差使。

量子场论的困难

在我1994年剑桥的旅行中最快乐的时光，就是与我的老朋友罗杰·彭罗斯爵士共进午餐。彭罗斯爵士那时刚获得了爵位，我和安妮去牛津对他进行祝贺。

我们四个人——我、彭罗斯，还有我们的妻子——坐在切尔韦尔河岸上的一个舒适的室外饭店，看着乘方头浅平底船的人们从身边经过。可能你并不太熟悉这项运动，撑平底船是一项优雅的划船运动，它通过撑篙推动船缓缓前进。这项运动富于田原风味，总让我想起雷诺阿（Renoir）的《游艇上的午餐》^[173]，但是还是有它的惊险之处。当一艘载有一群正在唱歌的本科生的小船经过时，那位撑篙的漂亮姑娘把篙卡在泥里了。她不想把它搞丢，于是在小船滑离的时候还死死地抓住它不放。这一幕为我们的午餐提供了一个余兴的节目。

同时，我们正在分食巧克力奶油冻，它是我们餐后的甜点，所以四个人的注意力都集中在这块奶油冻上面。女士们吃完了她们的部分，我和彭罗斯还在继续享用这美味的深色的巧克力剩余的部分，同时我们在笑那个束手无策的撑船手（她自己也在笑）。我有趣地注意到，在和彭罗斯你一叉我一叉轮流吃巧克力的时候，我们都将剩下的部分切成两半。彭罗斯也意识到了这一点，于是开始了一场比赛，看谁能切到最后。

彭罗斯说道，希腊人很早就在想，物质到底是可以无限分割的，还是每一种物质都有一个最小的不可分割的小块——它们被称为原子。“你认为有巧克力原子吗？”我问道。彭罗斯说不记得巧克力是否是元素周期表上的一个元素了。不论怎么说，我们最终把巧克力奶油冻分割成了看起来像最小的巧克力原子一样的东西，而且如果我没记错的话，彭罗斯赢了。当另一条船驶过来的时候，撑船事件也愉快地结束了。

量子场论的问题在于它基于的想法是空间（时空）就像可以无限可分的巧克力奶油冻。不论你如何精细地切割，你总可以继续分割它。重大的数学难题都是关于无穷大：数字永远能够数下去，但是为什么它们不能一直进行下去呢？空间无限可分是怎么样，不能无限分割下去又是怎么样？我觉得无穷大这个概念是在数学家中造成迷乱的主要原因。

不论神智是否迷乱，一个无限可分的空间被数学家称为连续统。连续统的问题在于最小的距离上面依然可存有巨大的量。实际上，一个连续统并没有最小距离——在你细胞越变越小的无限回归之中，你也就随之消失，这种情况可以在任何一个层面发生。换句话讲，一个连续统可以在空间每一个微小的体积中，蕴藏无穷多比特的信息，不论这个体积多么小。

量子力学关于无穷小的问题特别棘手，在那里任何可以晃动的东西都在晃动，而且“每一件未被禁止的事情都是必定发生的”，甚至在绝对零度的空无一物的空间中，如电磁场等各种场都在晃动。这些晃动在每一个尺度上发生，从最大波长为几十亿光年一直到一个不超过数学上一个点的尺度。量子场的这种晃动可以在每一个微小的体积中储存无穷多的信息。这是一个挽救数学上灾难的良方。

每一个细小体积内那些可能存在的数目无限的信息，在费曼图中就表现为无限回归的子图，它们越退越小直至无穷。我先从一个简单的想法开始：传播子代表一个电子在时空上的移动，其从单个电子开始也以单个电子为终端。

电子要从a到b还有其他方式移动——例如，在移动过程中边抛边接光子的方式^[174]。

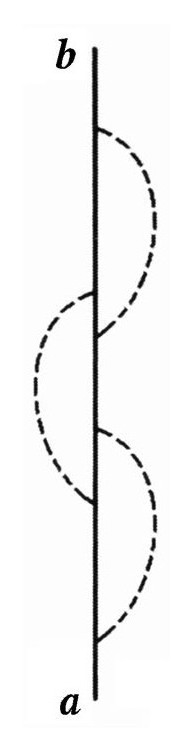
显然，这些可能性是无穷尽的，而根据费曼的规则，必须把它们都加起来才能知道实际的概率。每一幅图可以有更多的结构。每一个传播子和角点可以被一个更为复杂的结构所替代，这些结构包含着那些不受限制的嵌入图，直到它们实在太小而没法看到。但是利用高倍的放大镜，即便是再小的结构也可以继续下去，以至无穷。

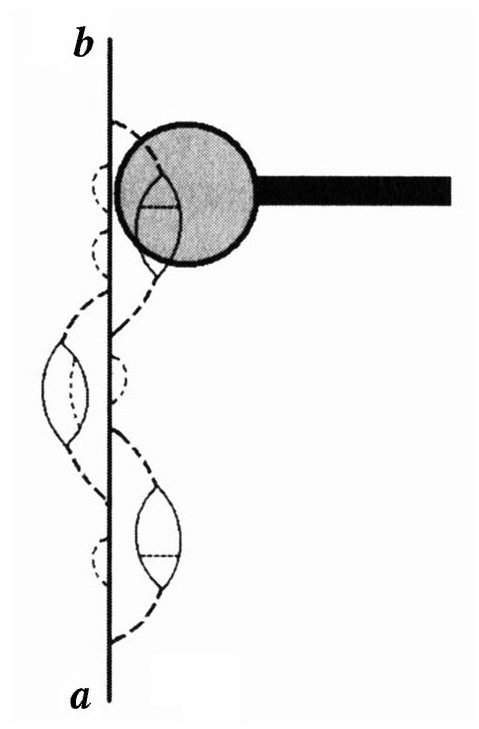
在量子场论中，关于时空连续统最令人不安的结果，就是你可以在费曼图上无限制地加入更小的结构：就像一个可以无限分割下去的巧克力奶油冻。

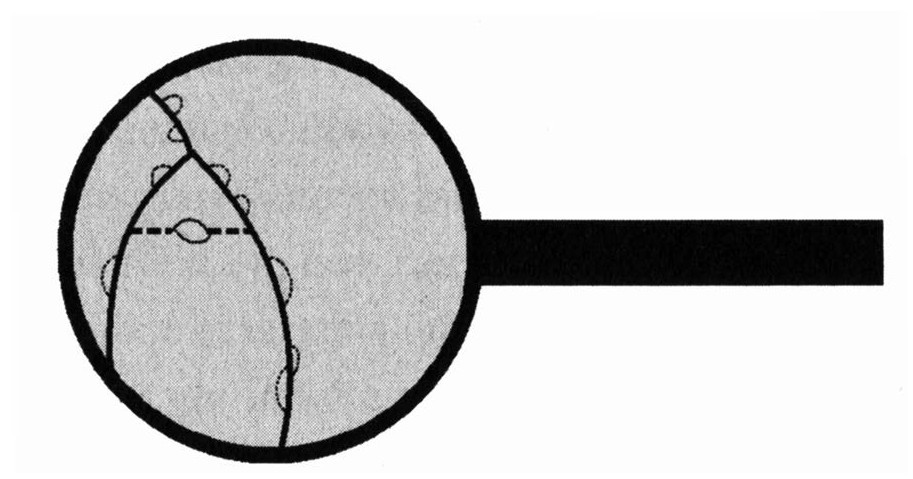
随着这些步骤的继续，你们对量子场论在数学上存在的危险，并不会感到惊讶了。把无穷多的、无限小的空间单元中的所有扰动集合成一个自洽的宇宙并不是一件容易的事情。事实上，大部分量子场论的版本是古怪且荒谬的。甚至基本粒子标准模型的最终分析可能在数学上也是不自洽的。

但是这些困难都不足以与建立引力的量子场论所遇到的困难相比。记住，引力是几何。在把广义相对论和量子力学结合的尝试中，根据量子场论的规则，人们必定会发现时空的形状一直不断地在变化。如果能够放大一个极小的空间区域，那么你可以看到空间在剧烈的抖动，空间自身扭曲成带有曲率的小突起和结的形状。而且你的放大倍数越高，那些扰动就会更剧烈。

假想的包含着引力子的费曼图反映了这种反常。这些无限变小的费曼图，最终会完全失去控制。每一种想要了解引力量子场论的尝试都会导致同样的结论：在这个最小尺度上发生了太多的事情。如果对引力应用量子场论的那些传统方法，必定导致数学上的溃败。

对于这个由空间的无限可分性而造成的灾难，物理学家们有一种办法可以将其消除：他们要求那个空间，就像一块巧克力奶油冻，不是一个真正的连续统。如果你不断地分割空间直至某一个点时，你很可能会发现一个不可再分的小块。换句话说，当结构变得很小的时候就停止画费曼图。这种分割的极限叫作截断。从更基本的观点看，一个截断无非就是把空间分割为不可再分的体像素，且不允许每个体像素上储存超过一个比特的信息。

截断看起来像是一种逃避，但是事出有因。经过长时间的思考后，物理学家们认为普朗克长度是空间的终极原子。只要你在尺度小于普朗克长度，或者与该尺度差不多大小的时候停止添加结构，费曼图就能正常工作，甚至是在那些包含引力子的情况下——至少在论证中是这样说的。这几乎是所有人对时空的期待——普朗克尺度上它有一个不可分的、颗粒状的、体像素的结构。

但是这些都是在发现全息原理之前。正如我们在第18章所看到的那样，用一个有限的普朗克尺度的体像素阵列来代替连续的空间是一个错误的想法。体像素空间严重高估了一个区域内所能发生的变化总数。它将使托勒密得到一个关于他图书馆所能存放的信息数的错误结论，也将理论物理学家们引向一个关于空间区域内能储存的信息总数的错误结论。

几乎从一开始人们就意识到，弦论可以解决无限小费曼图这个难题。它可以解决这个问题的部分原因，在于它摒弃了无穷小粒子这个想法。但是直到全息原理的出现，人们才意识到弦论与量子场论的截断版本或者体像素的版本有多么的不同。值得注意的是，弦论是一个典型的，描述了面像素宇宙的全息理论。

就像它的前身那样，现代弦论也有开弦和闭弦。在该理论的绝大多数但不是全部的版本中，光子是一个开弦且类似于介子，主要差别就是小了很多。在所有的版本中，引力子都是闭合的弦，类似于一个缩小版的胶子球。会不会有一些没有想到的更深刻的层面上，两种类型的弦，基本弦和QCD弦，是同一样东西呢？根据它们大小上的差异，看起来不太可能，但是弦论学家们怀疑尺寸上那么大的差异只是一种误导。在第23章，我们将看到有一种统一弦论的方式，但是现在我们暂且认为弦论的两个版本是不同的东西。

任何能形变，长度大于粗细的物体就是弦：鞋带和钓鱼线都是弦。在物理中，弦这个词还意味着有弹性的：弦可以延展也可以弯曲，就像蹦极绳和橡皮筋一样。QCD弦韧性很强——你可以在介子的一端吊起一辆硕大的卡车——但是基本弦的韧性更加强。实际上，尽管基本弦非常细，但是它们却具有令人难以置信的韧度——远远强于由普通物质构成的任何东西。基本弦能吊起大约10⁴⁰辆卡车。这个巨大的张力使我们很难将其拉伸至任何可以观测到的长度。结果就是基本弦的大小基本上就是普朗克长度。

对于那些我们每天生活中碰到的弦——蹦极绳、橡皮筋以及被拉长的口香糖来说，量子力学并不那么重要，而QCD弦和基本弦则具有很强的量子力学特性。与其他量子客体一样，这意味着能量是以离散的不可分割的单元增加的。从一个能量值到另一个能量值只可能以“量子跃迁”的形式来跨越这个能级台阶。

能量阶梯的底层被称为基态。加入一个单元能量得到的是第一激发态。再迈一个能级就是第二激发态，如此等等。通常的基本粒子，如电子和光子，都是处于阶梯的最底层。它们只能以量子零点运动的形式振动。但是如果弦论是正确的，它们可以旋转和振动以增加自身能量（因此质量也增加了）。

一根吉他弦是用拨片来拨动而激发的，诚如你所预料的那样，吉他拨片实在太大了，它无法用来拨动电子。最简单的方法就是，用一个电子去撞击另一个粒子。实际上，我们把一个粒子当作一个“拨片”来拨动另一个。如果碰撞足够强烈，它将使两根弦都处于振动的激发态。很显然，紧接着的问题就是，“为什么实验物理学不在加速器实验室中，激发电子或光子并彻底解决粒子是不是振动的基本弦这个问题呢？”问题在于阶梯实在太高。转动或者振动一个强子所需要的能量以现代粒子物理学的标准来说是很适度的，但是激发一根基本弦所需的能量则大得使人畏惧。给电子增加一单元的能量将使其质量达到一个普朗克质量。更糟的是，能量必定集中在一个小得令人难以置信的空间内。粗略地说，我们必须要把100亿亿个质子的质量，压缩入直径是质子的100亿亿分之一的小区域内。没有任何一台已经建造的加速器能接近这个要求。这样的事情从未做到过，很可能永远都做不到^[175]。

被高度激发的弦，平均说来要比它们基态时大；增加的能量冲击着弦拉长了它们。如果你可以轰击弦的能量足够大，那么它会伸展变成一个剧烈晃动的各部分互相缠结的纱线球。而且没有上限，只要用更多的能量，这根弦可以被激发到任何的大小。

如果不在实验室中，在自然界里却有一种办法可以创造出这种高度被激发的弦。如我们将在第21章所看到的，黑洞，甚至那些在星系中心的巨型黑洞，是一些极其巨大，互相纠缠的“怪物弦”。

还有另一个重要的令人着迷的量子力学结果。这个结果非常精妙，而且在这里阐述也可能会显得有点过于专业化。我们平常感觉的空间是三维的。关于这3个维度有许多术语：如经度、纬度以及海拔；或者是长、宽、高。数学家和物理学家通常用3个分别标记为x, y和z的坐标轴来描述这些维度。

但是基本弦并不太乐意仅在这三维中活动。我的意思是说，如果这样，那么弦论中精妙的数学会变得荒诞，除非空间有更多的维度。弦论学家在许多年前发现，除非再增加6个额外的维度，不然它们的方程在数学上是不自洽的。我一直认为，如果一件事情能得到足够好的理解，那么必定可以用非技术性的语言来解释的。但是弦论所需要的6个额外维排斥了简单性，即使在35年之后还是如此。我并不敢问心无愧地说：“……可以被证明。”

如果碰到一个能看到第四个、第五个维度的人，我会非常的吃惊，更不用说是9个维度了^[176]。我不可能比你做得更好，但是我可以给通常用的x, y，z添加字母表中的6个字母——r, s，t, u，v, w，然后用代数和微积分摆弄这些符号。有了这九个方向，弦论在数学上的自洽性便“可以被证明”。

现在你可能要问：如果弦论需要9个维度，而被观测到的空间只有3个维度，乍一看这不就是一个证明弦论是错的证据吗？但是事情没有那么简单。许多非常著名的物理学家——包括爱因斯坦、沃尔夫冈·泡利（Wolfgang Pauli）^[177]、费利克斯·克莱因（Felix Klein）^[178]、史蒂文·温伯格、默里·盖尔曼和史蒂芬·霍金（他们中没有弦论学家）——都认真地思考过这个想法：空间的维数高于三维。它们显然不是什么幻觉，所以一定有某种隐藏额外维的方法。关于隐藏额外维的行话叫作紧致化；弦论学家通过紧致化过程使这6个额外空间维紧致。这些空间上的额外维可以被卷曲到一个很小的“结”中^[179]，所以我们这些大型生物无法绕着它们移动，也无法发现它们。

一个或更多个空间维可以卷曲在微小的几何中，但因为太小而难以观测，这个概念是许多现代高能物理常见的主题。有些人认为额外维是一个臆想的产物，就像一句俏皮话所说的：“是带有方程的科幻小说。”但是这是一种由忽视所产生的误解。所有基本粒子的现代理论都利用某种额外维来提供那个缺失的机制，这使得粒子变得很复杂。

额外维这个概念并不是弦论学家发明的，但是他们使用的方式颇具创造性。虽然弦论需要6个额外维，但是我们只要给空间添加一个新的维度就可以了解其大概了。我们来研究一下额外维的最简单情形。我们给一个只有一维空间的世界——我们称它为线地——加上一维额外的紧致维。在线地上确定一个点的位置仅需要一个坐标；居住在那上面的人称其为X。

为了使线地世界更有趣一些，我们需要增加些物体，所以让我们假定存在着一些沿着线移动的点。

我们把它们看成是些小珠子，它们可以黏合在一起形成一个一维的原子、分子甚至是活的生命体。（我很怀疑生命是否能在一维的世界中生活，但是我们先把这种怀疑放在一边。）把线和珠子看成是无穷细的，这样它们就不会伸向其他的维度。或者更好的是，试着不用其他维度去想象线和珠子^[180]。

一个聪明的人可以设计出很多其他版本的线地。珠子都是相似的，或者在一个更加有趣的世界中，可能存在着一些不同种类的珠子。为了追踪不同的类型，我们可以用颜色给它们做标记：红色、蓝色、绿色，等等。我可以想象无穷多种可能性：红色珠子吸引蓝色的，但是与绿色的排斥。黑色珠子非常重，但是白色的是无质量的而且在线地以光速移动。我们甚至可以允许珠子是量子力学式的，任何一颗珠子的具体颜色都是不确定的。

一维的生活所受的局限非常大。它们只能沿着线运动，线地人总是互相撞击着。它们能够互相交流吗？很简单：它们可以发动它们身边的珠子，一个接一个的发送信息。但是它们的社交生活非常的无聊；每一个生物只有两个熟人——一个是它右边的，一个是它左边的。为了形成一个社交圈，至少应当是一个二维世界。

但是表象总是具有欺骗性。当线地人用一个高倍显微镜来观测时，它们会惊讶地发现它们的世界其实是二维的。它们所看到的并不是一个数学上理想的没有粗细的线，而是一个圆柱面。在通常的情况下，圆柱面实在太细了以至于线地人观察不到，但是在显微镜下面，小得多的物体，甚至比线地原子更小的东西都可以被发现。这些物体足够小，所以它们可以在两个维度上运动。

就像他们大人国的兄弟那样，这些线地小人国的居民可以沿着圆柱面的柱长方向移动^[181]，但是他们因为足够小，所以还可以绕着表面移动。他们可以在两个方向同时移动，绕着圆柱面螺旋运动。哦，有意思，他们甚至可以彼此通行，而不发生碰撞。他们有理由声称他们是生活在二维的空间中，但是有一点很奇怪：如果他们沿着额外维走一条直线，那么他们不久就又会回到原来的地方。

线地人需要给那个新的方向起一个名字，他们叫它Y。但是不像X，他们在Y上移动没多远就会回到出发点。线地人的数学家们就说Y方向是紧致的。

上面所给出的圆柱体的图，就是通常一维世界上增加了一维紧致方向后的样子。给一个已经有3个维度的世界增加6个额外维已经远远超出了人类大脑的想象能力了。物理学家、数学家区别于其他人的，并不是他们可以看到任意维度，而只是他们经过数学上艰辛的再训练——再次重新装备自己的大脑——来“看到”这些额外的维度。

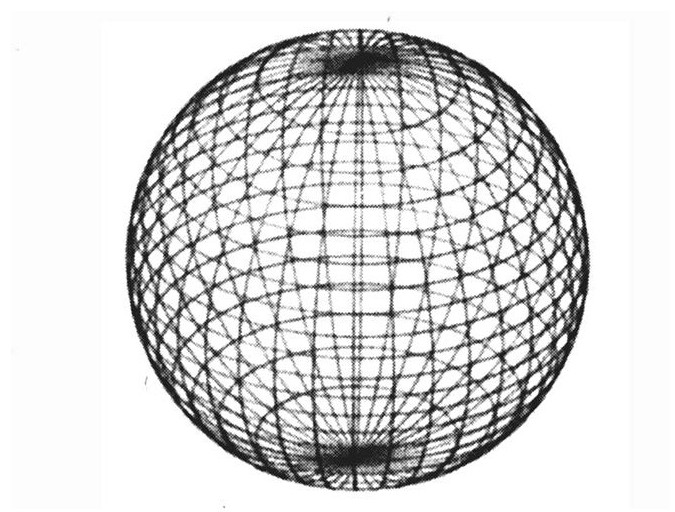
单个额外维并不会提供很多种变化的可能性。在紧致方向上的移动，就像绕着一个圈走，但自己却没有发现。但是两个额外维就允许了无穷多种变化的可能性。这两个额外维可以形成一个球面，一个圆环面（一个炸面圈的表面），^[182]

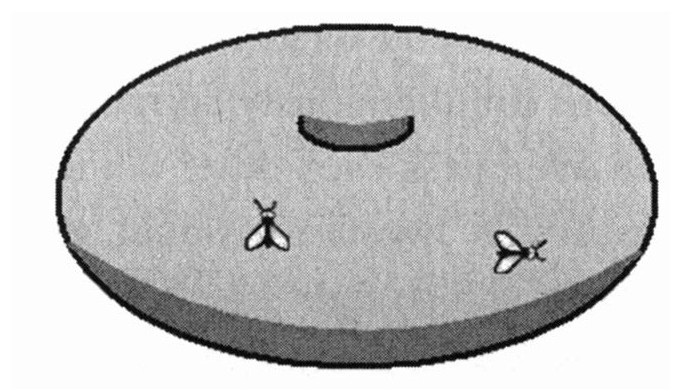
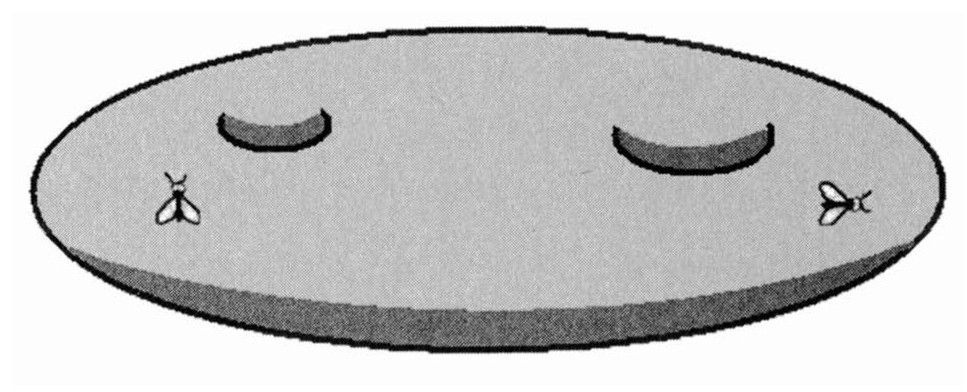
一个带有2个或3个孔的炸面圈

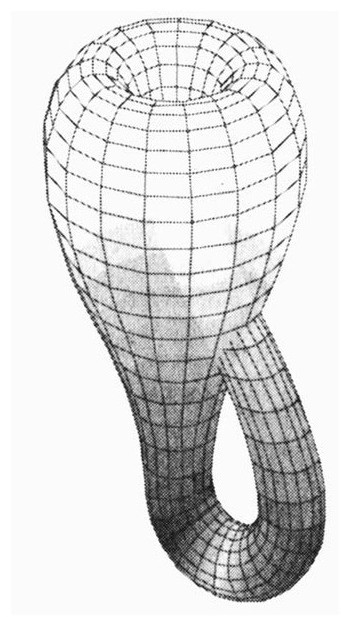
或者甚至是一个被称为克莱因瓶的诡异空间。^[183]

画出两个额外维并不是那么的困难——我们刚才就画过了——但是随着维数增加，去想象它们变得越来越难。到你增加到弦论所需要的六维时，不借助数学而凭空想象是不可能的。这种弦论学家用来紧致化这6个额外维的特殊的几何就被称为卡拉比—丘流形^[184]。而且这种流形有几百万种，没有两种是一样的。卡拉比—丘流形极其复杂，它带有几百个孔以及难以想象的椒盐卷饼式的扭曲^[185]。然而，数学家们可以通过切片的方法，降低它们的维度并画出它们，这类似于嵌入图。这就是一幅典型的卡拉比—丘空间的二维片层图。

我将试着向你们展示普通空间中每一个点上都加入一个卡拉比—丘流形后的样子。首先，我们来看那些通常的维度，像人这类的大型生物可以在其上面移动。（我把它画成了二维的，但是到现在你们应该能够在脑中加上第三维。）

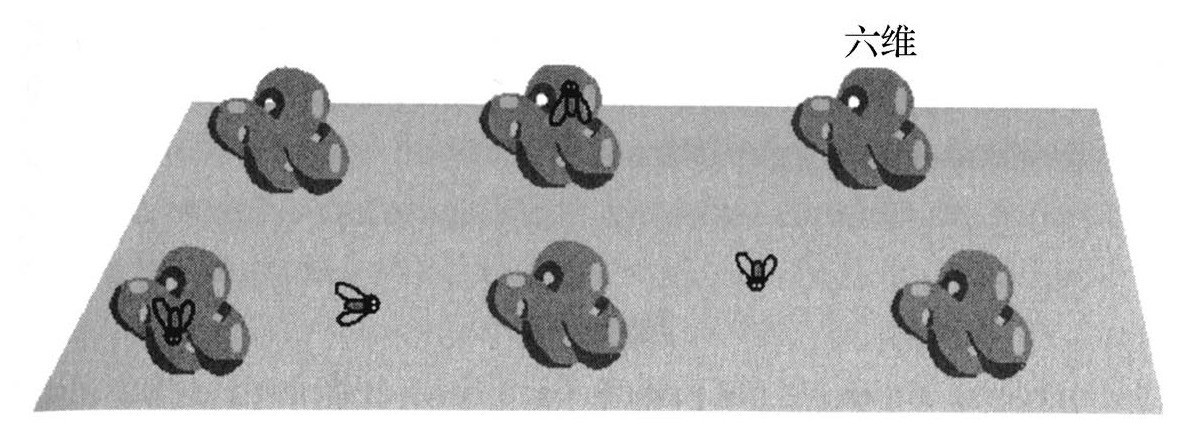
在三维空间的每一个点上还有其他6个紧致维，一些极小的物体可以在其上面移动。出于无奈，我所画的只能是分立的卡拉比—丘空间，但是你应该把它们想象成是分布在普通空间的每一个点上。

现在让我们回到弦上面。一根普通的蹦极绳可以往很多方向伸展——例如，沿着东西轴，南北轴抑或上下轴。它也可以以很多角度伸展，如朝北但是偏西10°。但是如果有额外维，会增加更多的可能性。特别是，弦可以绕着紧致方向延伸。一根闭弦可以绕着卡拉比—丘空间缠一圈或更多，而不沿着空间中的那些通常的方向延伸。

我想使问题更加复杂一点。弦不仅缠绕紧致空间，同时还在摆动，而且这种摆动会沿着弦传播，就像一条蛇那样。

将一根弦缠绕在一个紧致维上并使其摆动是需要能量的，所以由这些弦描述的粒子，要比通常的粒子重。

作用力

我们的宇宙不仅有空间、时间和粒子，还有作用力。作用在带电粒子上的电磁力，可以移动小片的纸和灰尘（回想一下静电力），但更重要的是，这些力使原子中的电子保持在它围绕原子核的轨道上面。作用在地球和太阳之间的引力，使地球在它的轨道上运动。

所有作用力根本上都是起源于单个粒子间的微观作用力。但是这些粒子间的作用力是从哪儿来的呢？对于牛顿而言，普适的质量间的引力是自然界的一个客观事实——一个他可以描述但无法解释的事实。在19世纪和20世纪，物理学家们，如迈克尔·法拉第、詹姆斯·克拉克·麦克斯韦、阿尔伯特·爱因斯坦和理查德·费曼，以他们深刻的洞察力用一些更为简单的基本概念来解释什么是作用力。

根据法拉第和麦克斯韦的理论，电荷并不是被直接地互相推拉；空间中电荷间有一种中间媒介在传递力。想象一个被两个相隔很远的球拉伸的“机灵鬼”^[186]——那些玩具软簧。

每一个球都只是在与机灵鬼相邻的那个部分作用上力。然后机灵鬼的每一个部分会把力作用到与它相邻的部分。这个力就这样顺着机灵鬼被传递下去直到与它拽动另一端的物体。看起来两个物体在互相推拽着，但这是一个由机灵鬼的软簧作为媒介而产生的假象。

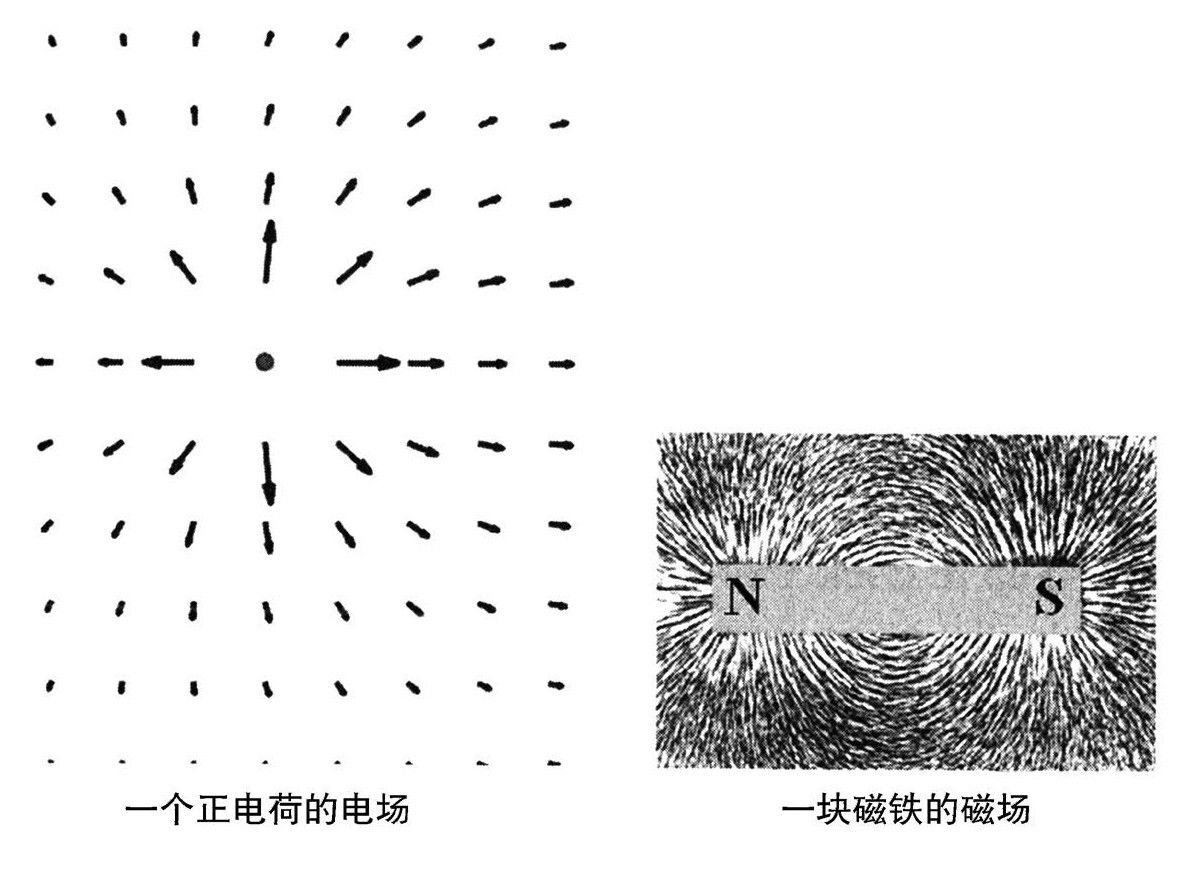
当问题变成带电粒子时，中间媒介就是充满空间的电场和磁场。虽然看不见，但这些场却是真实的：它们是些光滑的、看不见的空间扰动传递着电荷之间的力。

爱因斯坦在他的引力理论中，甚至走得更远。有质量物体弯曲了其邻近时空的几何，并且通过这样的方式，它们扭曲了其他物体的轨迹。这种几何的弯曲也可以被认为是一种场。

人们可能会认为这个问题已经结束了，直到理查德·费曼带着他关于作用力的量子理论出现，该理论乍看起来似乎与法拉第、麦克斯韦、爱因斯坦的场论完全不同。他的理论从带电粒子可以发射（抛）和吸收（接）光子这个概念开始。对于这个想法并没有什么争议，人们很早就知道当一个电子打在X射线管中的障碍物上时就会发射X射线。在那片光量子论文中，爱因斯坦首先描述了这种吸收的逆过程。

费曼把带电粒子描述成光子的杂耍者，不停地抛、接光子，也在其周围的空间制造大量的光子。一个静止的电子是一个完美的杂耍演员，不会掉一次棒。但是就像一个在火车车厢里的杂耍演员那样，突然的加速可能会失落东西。电荷可能会被拽离它原来的位置，因而在一个错误的位置吸收光子。这个遗漏的光子飞出去成了辐射光。

回到火车上，那个杂耍演员的拍档上了车，然后他们两个打算一起做一些团队协作的抛接杂耍。每一个杂耍演员接到了自己投出去的东西，但是当他们离地越来越近时，每个人时不时地会接到另一个人抛出去的球。同样的事情也发生在两个离得很近的电荷间。围绕在电荷周围的光子云混在了一起，而且一个电荷可能会吸收另一个电子所发射的光子。这个过程被称为光子交换。

光子交换的结果就是，电荷彼此施加作用力。只有通过精妙的量子力学才能知道力是吸引的还是排斥的。结果就是一句话，当费曼做了那些计算时，他发现了与法拉第和麦克斯韦所预言的一样的东西：同性相斥，异性相吸。

比较电子和杂耍演员的抛接是很有意思的。杂耍者每秒钟抛接的次数约为几次，但是一个电子每秒钟大约能发射和吸收10¹⁹次。

根据费曼的理论，不止是电荷，所有物质都在抛接。每种物质都发射和吸收引力子，引力场的量子。地球和太阳被引力子云所包围，这些引力子混合并且交换。结果就是引力使得地球保持在自己的轨道上运动。

单个电子多久会发射一个引力子呢？答案出人意料：并不是很经常。一般来说需要比整个宇宙年龄更长的时间来使电子辐射一个引力子。这就是为什么根据费曼的理论，基本粒子间的引力强度比电磁力小得多。

所以哪个理论是正确的：法拉第、麦克斯韦、爱因斯坦场论还是费曼的粒子抛接理论？它们彼此听起来是那么不同。

但是它们都是正确的。关键就是在第4章中解释过的波和粒子之间的量子互补性原理。波是一个场的概念：光波无非就是有一个快速波动的电磁场。但是光又是粒子，即光子。所以费曼关于力的粒子图像和麦克斯韦的场图像是量子互补性原理的另一个例子。由抛接粒子云所制造的量子场被称为一种凝聚。

一个关于弦的笑话

给你讲一个最近在弦论学家间很流行的笑话。

两根弦走进了一个酒吧，然后要了几杯啤酒。服务生对他们其中一个说：“嘿，好久不见。最近怎么样？”然后他对另一根弦说：“你是新来这里的，是吗？你跟你朋友一样是闭弦吗？”第二根弦回答道：“不，我是一个磨散的结。”

好吧，你希望从一个弦论学家身上得到什么东西呢？

这个笑话到此结束，但是故事得继续下去。那个服务生感到有点晕晕乎乎。大概是因为吧台后面有太多秘制的饮料，也有可能是这两个顾客不断闪烁的量子扰动使他发晕了。但是，这并非是普通的晃动，弦似乎运动得非常奇怪，好像有某种隐藏的力在用力拽它们，想把它们结合到一起。每当一根弦突然移动一下时，另一根会紧接着在它的高脚凳上被拽一下，反过来也同样。但是看起来并没有什么东西连接着它们。

服务生对这种诡异的行为很好奇，想找到某些线索，就盯着它们之间的空间看。起初他所能看到的只是微弱的闪烁，一个令人眩晕的几何上的扭曲，但是看了1分钟之后，他发现不断有一些小东西从两个客人身体上脱落下来，形成它们之间的一个凝聚物。正是这个凝聚物推搡着它们。

弦发射和吸收其他的弦。我们以一个闭弦为例子。除了只在零点附近做晃动，一个量子弦可以分裂成为两根弦。我将在第21章中描述这个过程，但是现在一个简单的图像可以给你一个概念。这就是一幅闭弦的图。

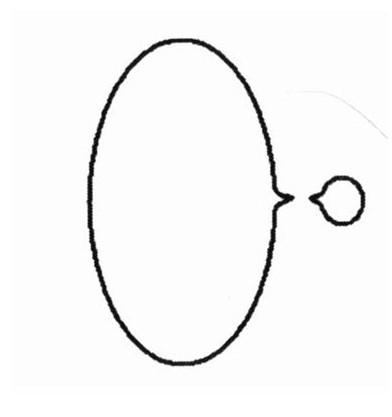
这根弦微小地摇动着直到一个耳朵形状的附加物出现。

这根弦已经可以分裂了，放出它自己的一小部分。

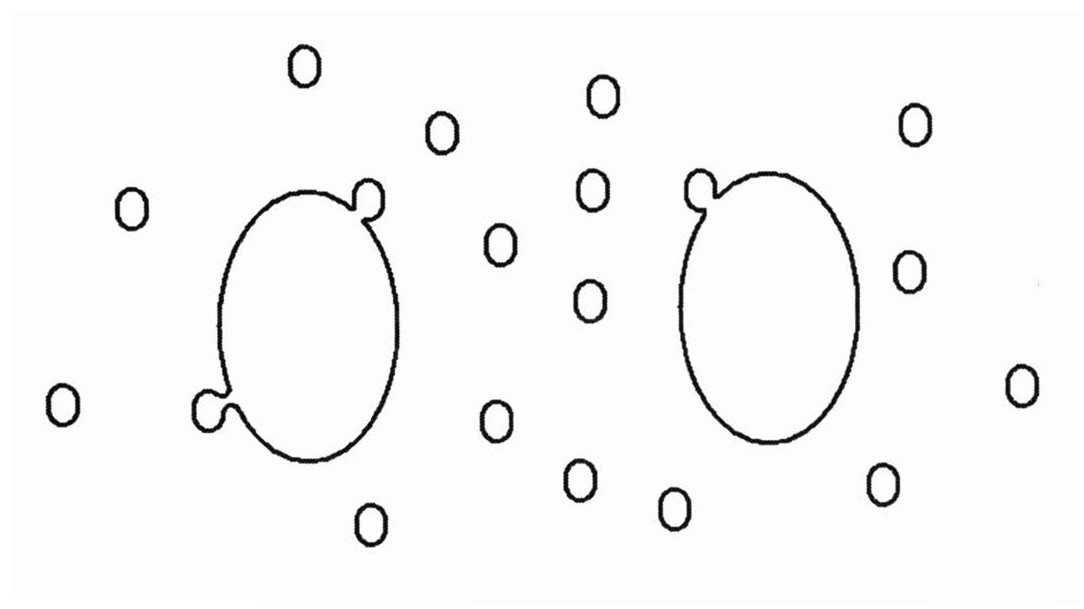
反过来也是可能的：当一根较小的弦遇到另一根大一些的弦，它将会通过逆过程而被吸收。

服务生看到的是那些小的弦的凝聚物——就像飘浮的量子云——包围着他的客人。但是当他看得不是那么仔细的时候，这个模糊的凝聚物看起来仅仅发生弯曲，他的视线就像一个弯曲的时空区域所作的。

这些细小的闭弦圈是引力子，它们云集在较大的弦附近并形成一种凝聚物来模拟引力场的效应。引力子是引力场的量子，在结构上与核物理中的胶子球类似，但是引力子的尺寸是后者的1/10¹⁹。如果它真的存在的话，有人会问这一切对于核物理来说又意味着什么。

弦论学家的热情，让一些其他领域的物理学家们觉得很气愤。弦论学家认为：“弦论中漂亮、优雅、自洽、坚实的数学会导致一个令人吃惊的、难以置信的结果，该结果能自动导出引力，所以它必定是对的。”但是对于那些持怀疑态度的、不是弦论圈子里的人来说，即使弦论中一些东西已被证明，弦论并非好到足以让我们得到一个令人信服的理论。如果弦论是关于自然界的正确理论，那么证实它的方式就是通过令人信服的实验预言和经验检测，而不是逻辑。他们是对的，但是弦论学家也是对的。真正的问题在于对这些尺寸是质子的100亿亿分之一的物体进行实验是极其困难的。但是不论弦论最终是否能得到实验数据的证实，在这个自洽的数学实验室中，我们可以检测各种关于引力与量子力学结合的想法。

假定引力会出现在弦论中，我们可以假设当弦的质量足够大的时候，就会形成一个黑洞。所以弦论是一个框架，在那里霍金的佯谬是可以得到检验的。如果霍金是对的，那么黑洞不可避免地导致信息丢失，弦论的数学会证明这个结论。如果霍金是错的，那么弦论会告诉我们信息是如何逃离黑洞的。

在20世纪90年代的早期，我和赫拉德·特霍夫特之间曾有3次互访，两次在斯坦福，一次在乌得勒支（如果我没记错的话）。特霍夫特基本上是不相信弦论的，尽管他曾写过一篇有重大影响的文章解释了弦论和量子场论之间的关系。我不能确定他讨厌的根源是什么，但是我能猜到其中部分原因在于，从1985年开始美国所建立的理论物理学机构，居然清一色地由弦论学家所主导。特霍夫特，这个永远的针锋相对者，相信（我也是）多样性的力量。你对待问题的方式越是不同，那么你的思想风格就越不同，解决科学上真正难题的机会就会越多。

然而对于特霍夫特来说，更重要的是他的怀疑不只在于反感，那种物理学被狭小的一群人掌管所带来的反感。我所能说的就是，他承认弦论的价值，但是他排斥弦论是“终极理论”的主张。弦论的发现是一个偶然，而且它的发展道路一直很崎岖。我们从未有过一组总的方程或者一组确定的精简的方程。即使到了今天，它包含了一个相互联系的数学网络，这些数学以引人注目的方式聚合在一起，不过它们并不能增加以牛顿引力理论、广义相对论和量子力学为特征的原理约定集合。而是，就像一个非常复杂的拼图玩具，我们只能很模糊地感受到这整幅图。记住在这章开头所引用的特霍夫特的话：“试想我给你一把椅子，同时又跟你解释说，椅子还没有腿，坐板、靠背和扶手也许一会儿会送过来；不论我真正给了你什么，我还能称其为椅子吗？”

弦论确实还不是一个完整的理论，但是就现况而言，它是我们最好的数学向导，指引我们通向量子引力的终极原理。而且，我想补充的是，它是黑洞战争中最有力的武器，特别是证明特霍夫特他自己的那些信念。

在接下来的三章中，我们将看到弦论如何帮助解释和确认黑洞互补性原理、黑洞熵的起源以及全息原理的。

第20章　最后的螺旋桨

对于大部分物理学家来说，特别是那些广义相对论的专家，黑洞的互补性原理实在是太疯狂了，这不可能是真实的。他们并没有对量子效应所产生的含糊性感到不舒服；普朗克尺度上的含糊是完全可以接受的。但是黑洞互补性原理所提议的东西要激进得多。根据观测者的运动状态，一个原子可能是一个微观的小物体，或者它可能弥散在一个巨大黑洞的整个视界面上。人们确实无法接受这么含混的东西，连我自己也觉得很奇怪。

就像我在1993年圣芭芭拉会议结束后几周中所思考的，这种奇特的行为，让我想起以前看到过的一些东西。24年前，那时弦论还属幼年时期，我正被这些微小的类弦物的某种未知特性所困扰。我那时称这些代表基本粒子的弦为“橡皮筋”。

根据弦论，世界上每一个物体都是由一维的有弹性的弦构成，这些弦能拉伸、弹拨和绕转。我们把粒子看作一个比普朗克尺度大不了多少的微型橡皮筋。如果一根橡皮筋开始晃动和振荡，假设橡皮的各个部分之间没有摩擦力，那么这种晃动和振荡会永远继续下去。

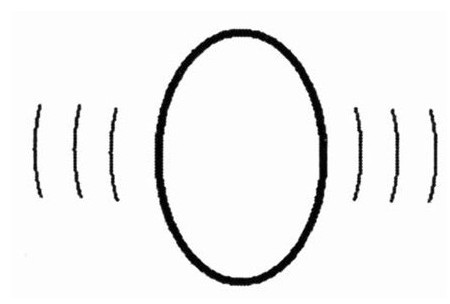
增加弦的能量会使弦振荡得更加剧烈，有些时候看起来像是一团巨大的剧烈振荡的纱线。这些振荡是热振荡，它们给弦增加了真实的能量。

但是我们不能忘记量子晃动。即使在一个没有能量的系统中，即系统处于其基态，晃动也不能完全被去除。这些基本粒子的复杂运动是奇妙的，但是通过类比，我可以告诉你其中的一些奥妙。首先我要讲的是关于狗哨和飞机螺旋桨的故事。

由于某些原因，狗对高频率声音很敏感，甚至是许多人不能听到的频段。也许是狗的耳鼓更轻盈些，所以能够察觉更高频率的振动。因此，如果你想叫你的狗，但是又不想打扰你的邻居，那么你可以使用一个狗哨。狗哨的声音频率很高，人的听力系统对它没有反应。

现在设想爱丽丝跳进一个黑洞，并且吹响她的狗哨，来给她留给鲍勃照看的雷克斯^[187]发了一条信息^[188]。这个频率对于鲍勃的耳朵来说太高了，起初他什么都没有听到。但是想一下，一个信号若在视界附近发出将会发生什么呢？从鲍勃的角度来看，爱丽丝和她所有的身体机能，似乎都在慢下来，其中也包括她哨子声音的频率。虽然这个声音一开始超出了鲍勃的听域，但是随着爱丽丝慢慢靠近视界，鲍勃渐渐可以听见哨声。假定爱丽丝的狗哨覆盖了整个高频段，有些甚至超过了雷克斯的听域。鲍勃会听到什么？起初什么也听不到，但是不久后，他便慢慢听到一些哨子发出的最低频率的声音。随着时间推移，更高一点的也能听到了。最后鲍勃能听到爱丽丝哨子所吹出的整个交响乐曲。当我跟你讲关于飞机螺旋桨的故事的时候，你脑子里面要留着这个故事的印象。

你应该看过飞机螺旋桨逐渐变慢直到停止的样子吧。开始的时候那些叶片是看不见的，你只能看到中间的毂。

但是当螺旋桨慢下来，频率低于每秒钟30转后，可以看到叶片了，整个装置也变得更大了。

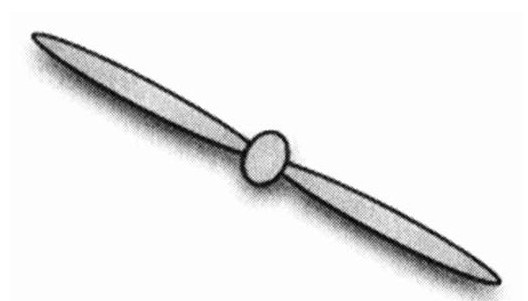
现在设想一只带有“复合”螺旋桨的飞机。我们称其为爱丽丝的飞机。每只叶片的尖上有一个轴，上面装了一只“第二级”的螺旋桨。这只第二级的螺旋桨要比原先的那只转得快许多——我们先定为快10倍。

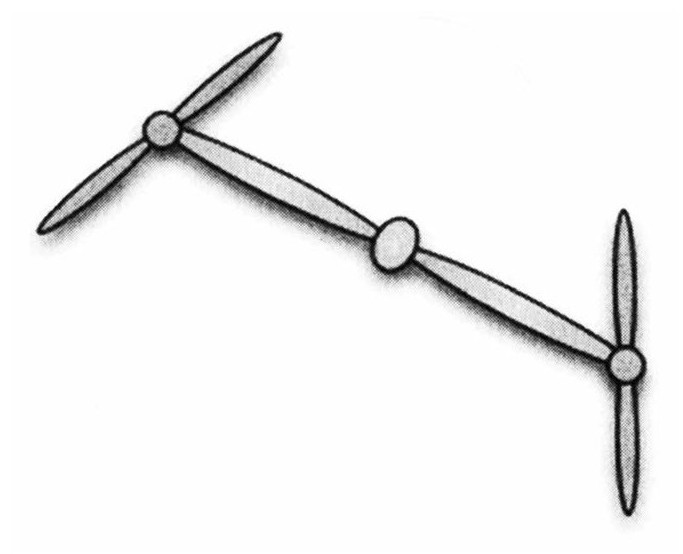
当第一级螺旋桨可以看到的时候，第二级螺旋桨还是看不到的。随着桨的转速变慢，第二级螺旋桨也看得见了。这个结构似乎还可以继续下去。第三级螺旋桨被装在了第二级螺旋桨的末端。那些螺旋桨的转速是第二级螺旋桨的10倍。这需要更长的时间把速度降下来，但是这个复合式的螺旋桨将不断延伸开去，其面积越来越大。

爱丽丝的飞机并不仅停留在第三级上面。它的螺旋桨将无限制地扩展开去。随着它不断变慢，人们便可以看到越来越多的螺旋桨。整个装置越变越大，最终变得巨大无比。但是除非螺旋桨完全停止，否则你所能看到的螺旋桨的级数永远是有限的。

很容易想到，下一步就是爱丽丝驾驶她的飞机径直地飞向一个黑洞。这时鲍勃会看到什么呢？根据我已告诉你的，特别是关于黑洞和时间机器，你自己便可以得出结论。随着时间的推移，螺旋桨会慢下来。最终，第一级螺旋桨出现了，接着可以看到越来越多的螺旋桨，逐级涌现出来，最终覆盖整个视界。

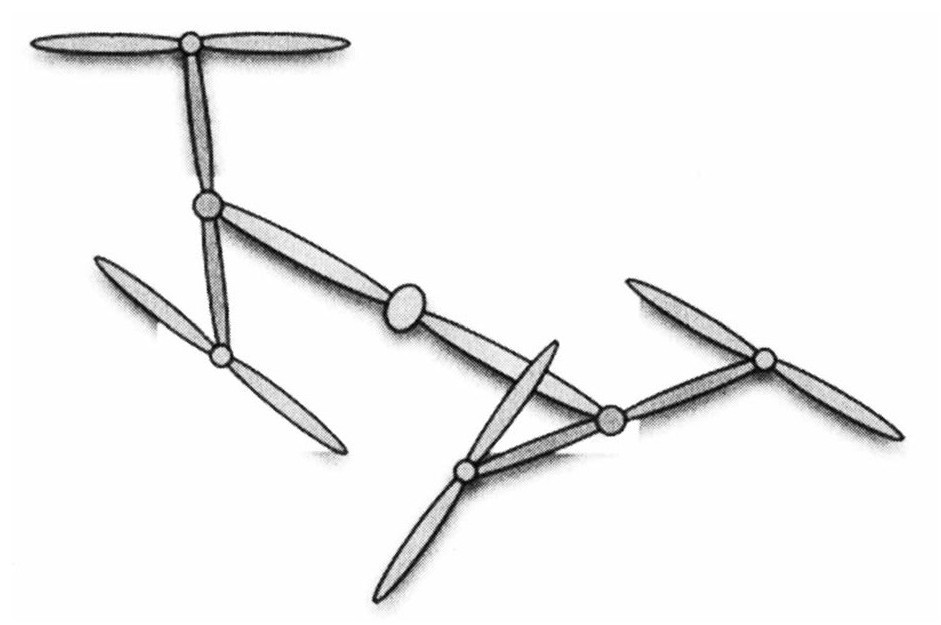
这就是鲍勃将会看到的。但是随着螺旋桨一起运动的爱丽丝将看到什么呢？没有任何特别的事情。如果她正在吹她的狗哨，那么这个声音对她来说还是听不见的。如果她朝螺旋桨看，那么叶片还是转得太快以至于她的眼睛或相机都看不见。她将看到你和我在看一个高速旋转的螺旋桨时所看到的——仅是桨的中心毂，而没有其他别的东西。

你可能会认为这样的图像有些不对劲。爱丽丝可能看不见高速转动的螺旋桨，但是如果说它们是不可观测的似乎又有点儿太过分了。毕竟，它们可以轻易地把她切成碎片。实际上，对于真实的螺旋桨来说，这是真的，但是我现在所描述的模型更加的微妙。回忆一下第4章和第9章，我解释说自然界中有两类晃动：量子晃动和热晃动。热晃动是危险的；它们可以把能量转移到你的神经末梢或者是做一份牛排。如果温度足够高的话，它们可以撕裂分子或原子。但是不论你让你的牛排待在一个冷的、没有东西的真空的空间中多久的时间，电磁场的量子扰动并不会有什么效用，它还是完全生的。

在20世纪70年代，黑洞理论学家们如贝肯斯坦、霍金特别是威廉·温鲁（William Unruh）证明了在一个黑洞视界附近，热晃动和量子晃动以一种奇怪的方式混合在一起。对于穿越视界的人来说晃动似乎是无害的量子扰动，而对于选在黑洞外面的任何东西来讲晃动就变成了极其危险的热扰动。就像爱丽丝那些转动的螺旋桨是量子晃动（对于爱丽丝来说看不见），但是当它们在鲍勃的参考系下变慢时，它们就变成了热晃动。如果鲍勃悬在视界表面的话，爱丽丝无法察觉的这些温和的量子运动，对他来说是极其危险的。

到现在你可能对黑洞互补性原理已经有所了解。实际上，这与我在第15章中所解释的关于一个原子掉入黑洞的情况非常相似。因为这是5章前的东西了，这里快速地回顾一下。

设想当爱丽丝掉向视界时，她回头看后面紧跟着的原子。原子看起来很正常，甚至当它穿越视界的时候。它的电子继续以平常的速度绕着原子核旋转，而且它看起来并没有比其他原子更大——大概就是这页纸的10亿分之一的大小。

对于鲍勃来说，他看到原子在接近视界的时候慢了下来，而且与此同时热运动把它撕成了碎片并散落在一块不断变大的面积上。原子看起来就像一架微型的爱丽丝的飞机。

我的意思是原子有螺旋桨，螺旋桨上又有螺旋桨，这样无限循环下去吗？出乎你们的意料，我就是这个意思。基本粒子一般被想象成非常小的物体。爱丽丝的复合螺旋桨的中心看起来也很小，但是整个装置，包括所有级结构，极为巨大甚至是无穷大的。我们在说粒子很小的时候，我们有没有可能搞错了？实验上是怎么说的？

在思考关于粒子的实验观测的时候，把每一个实验都想象成一个类似于给运动物体照相的过程是很有益处的。捕捉高速运动的能力取决于相机记录图像的速度。快门的速度是时间分辨率上一个重要测量量。显然，快门速度将对爱丽丝的复合螺旋桨的摄影过程起关键作用。一台较慢的照相机能抓住的只是螺旋桨的中心毂。一台快一些的照相机可以捕捉到另外一些高频率的结构。但是，即便是最快的照相机也只能捕捉到复合螺旋桨的某个部分——除非是在当飞机掉入黑洞的时候拍摄它。

在粒子物理实验中与快门速度相应的是碰撞粒子的能量：能量越高，快门越快。对于我们，不幸的是，快门速度严格地受制于粒子加速至高能的能力。理想情况下，我们可以分辨在比普朗克时间小的时间区域上发生的事情。这需要一些正在加速到比普朗克质量还大的粒子——原则上很简单，但是实际是不可能做到的。

我们在这里稍作停留，想一下现代物理所面临的巨大困难。为了观测最小的物体和最快的运动，20世纪的物理学家依赖于越来越大的加速器。第一台加速器只有桌面大小，非常简易，可以用于探测原子的结构。原子核则需要更大的机器，有些跟建筑物一样大。夸克只有用那些有几英里长的加速器才能被发现。现在最大的加速器，瑞士日内瓦的大型强子对撞机，周长约有20英里，但是还是太小，无法把粒子加速到普朗克质量。多大的加速器才能分辨出普朗克频率下的运动呢？这个答案是令人沮丧的，简单来说：为了加速一个粒子到普朗克质量，加速器至少要与我们的星系一样大。

简而言之，用现代技术来看普朗克运动，就好比用一个曝光时间为1000万年的相机来给转动的螺旋桨拍照。基本粒子看起来很小，这是因为我们所看到的只是中心部分，显然是情理之中的事情。

如果实验不能告诉我们，粒子是否具有边远的高频振荡的结构，我们必须依赖于我们最好的理论。在20世纪的下半叶，研究基本粒子最有力的数学框架就是量子场论。量子场论是一个令人兴奋的领域，开始的时候它假设粒子很小，可以被看成仅仅是空间上的一些点。但是这样的图像不久就崩溃了。粒子很快地被更多的粒子所包围，这些粒子飞速地过来又飞速地离开。而这些新过来的和新离开的又被甚至更快出现和消失的粒子所包围。用快门速度更快的照相机，就可以看到粒子越来越多的内部结构——振荡越来越快的粒子出现和消失。一个慢速的照相机看到的分子就是一团模糊。只有在快门速度快到能抓住原子运动的时候，它才会显示出一群原子的样子。这个故事在原子层面上不断地重复着。对于原子核周围那一团电荷所形成的模糊，只有在更快的实验中才能分辨出来是电子。原子核分辨成为质子和中子，它们又分辨成为夸克，以此类推。

但是，这些曝光越来越快的照片，并不揭示一个占据越来越多空间的膨胀的结构，而这正是我们在找寻的主要特性。反而，它将告诉我们越来越小的粒子形成像俄罗斯套娃式的层次结构^[189]。这不是我们解释粒子在视界附近行为所需要的。

弦论则要有前途得多。弦论所说的东西是与直觉违背的，所以多年来物理学家们都不能了解它。弦论所描述的基本粒子，那些假设的细小弦圈，就像复合的螺旋桨一样。我们从一个慢速的快门开始，这时一个基本粒子看起来就像一个点；可以看成是螺旋桨的中心。现在加快快门的速度，直到曝光时间只比普朗克时间长一点点。图像所显示的粒子就是一根弦。

若把快门速度提得更高，你所看到的是正在扰动和振荡着的弦上的每一个部分，所以这个新的图像看起来更加的混乱，铺开的面积也更大。

但是这仍不是尽头，过程还将不断地重复。每一个小弦圈、弦的每一次弯曲，都会分解为扰动更加剧烈的弦圈和波形曲线。

当鲍勃注视着一个类弦粒子掉向视界时，他看到了什么？起初，振荡很快而看不清楚，他所看到的只是一个微小的类毂的中心。但不久之后，接近视界时的特有性质开始起作用了，弦的运动显得慢了下来。他渐渐地可以看到越来越多振荡的结构，就跟他看爱丽丝的复合螺旋桨一样。随着时间的推移，速度更快的振荡可以被看到了，弦看起来越长越大，并且布满了黑洞的整个视界。

但是如果我们随着粒子一起掉下去又会怎样呢？那么，这是一个很正常的时期。高频的扰动还是高频的扰动，远远超过我们低速相机的频率范围，处在视界附近没有给我们什么优势。就如同在爱丽丝的飞机的情况中，我们能看见的就是细小的毂。

弦论和量子场论都认为事物会随着快门速度的增加而变化。不过在量子场论中，物体是不会变大的。与此相反，它们似乎会分裂成为越来越小的物体，更小的俄罗斯套娃。但是当各个组分接近普朗克长度时，一个全新的模式就出现了：爱丽丝飞机模式。

在拉塞尔·霍本（Russell Hoban）的寓言《老鼠和他的孩子》中^[190]，有一个很好玩的（不是特意的）故事，可以用来比喻量子场论是如何工作的。曾经在它们噩梦般的历险中，这两只玩具机械鼠，鼠爸爸和儿子发现了一罐令他们无比着迷的梵僧牌狗粮^[191]。在罐头的标签上画着一只狗拿着一罐狗粮，这罐狗粮的标签上又画着一只狗拿着一罐狗粮，如此等等。为了看到“最后一只可以看到的狗”，老鼠们一层一层地往下看，但是它们永远不能确信自己已经看到了它。

东西里面藏着东西，东西里面又藏着东西——这就是量子场论的故事。然而，与梵僧牌的标签不同，物体是移动的，它们越小移动得越快。所以要看到它们，你需要一个很厉害的显微镜和一个速度很快的照相机。但是注意一件事情：不论是分解分子还是那罐梵僧牌狗粮似乎都不是越来越大，就像越来越多的结构被发现一样。

弦论则不同，它的方式更像是爱丽丝的飞机。随着事物的速度减慢，越来越多的弦状的“螺旋桨”就会进入视线。它们占据空间中越来越多的位置，整个复杂的结构跟着增长。当然，爱丽丝的飞机是一个类比，但是它抓住了弦论的许多数学特性。弦，跟其他任何东西一样，有量子晃动，但是方式却很特殊。就像爱丽丝的飞机，或者她的狗哨的乐曲版本，弦以许多不同的频率振动。大部分的振动速度太快而无法被发现，即便是用强大的粒子加速器所提供的高速快门也无法捕捉。

当我在1993年开始意识到这些的时候，我也开始理解霍金的盲点。对于大部分量子场论出身的物理学家来说，带有晃动结构的、不断变大的、无边界粒子的概念是极其怪异的。具有讽刺意味的是，唯一暗示了存在着这些可能性的人，就是这个世界上最伟大的量子场论学者，我的战友赫拉德·特霍夫特。虽然他用他自己的方式陈述了这个想法——不是用弦论的语言，但是他的工作也表达了随着检测时间的分辨率的提高，物体会变大的想法。相比之下，霍金的策略锦囊中装的是梵僧牌狗粮而不是爱丽丝的飞机。对于霍金来说，量子场论和它的点粒子是微观物理的全部和终结。

第21章　数黑洞

一天早上，我从楼上下来吃早饭。我的妻子——安妮对我说，你把T恤穿反了，把编织的V形穿在背面了。后来当我从外面慢跑回来的时候，她笑着说：“现在是把里面穿在外面了。”于是我就开始琢磨，穿一件T恤有多少种方式？安妮嘲笑着说：“你们物理学家就喜欢思考这种愚蠢的问题。”为了证明我超凡的智慧，我马上声明，穿一件T恤有48种方式。首先，你可以将你的头穿过4个洞中的任意一个。现在剩下了3个洞给你的躯干。挑完一个给脖子一个给躯干，还剩两个机会给你的左臂。一旦你选择了你的左臂，那么只有一个选择留给了你的右臂。所以这就意味着4×3×2=24种方式可以选择。但是你可以把T恤里外反着穿，这样又是另外的24种，所以我很自豪的宣布我解决了这个问题：48种方式来穿一件T恤。安妮并不感到吃惊。她回答道：“不，有49种，你还忘了一种。”我很困惑地问道：“我遗漏了哪一种？”她说：“你可以把它揉成一个球然后随手一扔……”你知道我的意思了吧^[192]。

物理学家们（或许还包括数学家们）对于数数目非常在行——特别是数可能性。计算可能性是了解熵的中心思想，但是在黑洞的问题中，我们究竟应该计算什么呢？肯定不是一个黑洞能用多少种方式来穿一件T恤。

为什么计算黑洞有多少种可能性那么重要呢？毕竟，霍金在他计算得到熵等于普朗克单位下视界面积的时候已经给出答案了。但是关于黑洞的熵仍有许多的困惑。下面就来告诉你个中原因。

霍金认为关于熵就是隐含信息的整个想法——如果你知道细节的话，信息是可以计算的——在考虑黑洞的时候一定是错的。他并不是唯一这么说的人。几乎所有的黑洞专家都得出同样的结论：黑洞的熵是不一样的，与计算量子态个数没有任何关系。

为什么霍金和相对论学家们会有这么激进的一个想法呢？问题在于霍金的论证颇具说服力，他认为人们可以朝黑洞里面不断地丢信息，但却没有任何信息会流出来——就像把无数个小丑塞入小丑车中一样^[193]。如果熵是通常意义上的熵，即，所有可能被隐藏在黑洞中的可能的信息的总数，那么这些被隐藏的信息总数一定是有限的。但是如果有无穷多的比特掉进了黑洞，那么这将意味着黑洞熵的计算无法囊括所有隐藏的可能性——而且这也意味着，物理学中一个最古老的最受信任的分支——热力学，需要一个革命性的新基础。因此，了解黑洞熵是否真的计算了一个黑洞所可能有的结构，就变得非常紧迫。

在这一章中，我将告诉你们，弦论学家是如何计算的，以及他们是如何给出一个关于贝肯斯坦—霍金熵的量子力学基础的——一个能排除信息丢失的可能性的基础，这些工作仍在进展中。这是主要的成就，而且它在反对霍金观点的征途上，走了很长一段路，黑洞不能吞噬信息。

但是，首先让我解释一个观点，这是由赫拉德·特霍夫特最早提出来的。

特霍夫特的猜想

自然界中有许多不同的基本粒子。说物理学家们并不完全了解，是什么使得它们彼此不同，这并不为过。但是如果不去问一些深层的问题，我们还是可以从经验的角度，去观察所有这些由实验上得知的或是从理论上预言的粒子。为了将它们都展示出来，我们把它们都画在一根轴上面，画一幅类似于基本粒子谱的图。横轴表示质量，左边端点是最轻的物体，朝右边质量逐渐增加。竖线表示具体的粒子。

在能量较低的那端是那些人们熟悉的粒子，我们已经确定它们的存在。其中有两个没有质量并以光速移动的是光子和引力子。接下来是中微子、电子和一些夸克、μ轻子、另外一些夸克、W玻色子、Z玻色子、希格斯玻色子以及τ轻子。这些名字和细节并不重要。

在质量稍大些的一段上，有这么一群粒子，虽然它们的存在只是一个猜测，但是许多物理学家（包括我）都认为它们很可能存在^[194]。由于这里我们并不太关心这些粒子，所以将这些假想的粒子统称为超对称伙伴。在超对称伙伴后面是一个很大的空白区，我用问号标注了出来。这并不是说我们知道这是一个空白区，只是没有什么特别的理由来假设，在这个区域上存在着什么粒子。而且，没有一个在建的或者是预期要建的加速器，可以有足够的能量去产生这么大质量的粒子。所以这个缺口是一片未知领域。

然后当质量标度远大于超对称伙伴的时候，我们看到的是大统一粒子。这些也是假想的粒子，但是我们有充分的理由相信它们的存在——在我的观点中，它们比超对称伙伴更有存在的理由——但是人们最多也只能是通过间接的方式发现它们。

在我的示意图中最具争议的粒子就是弦激发粒子。根据弦论，这些粒子是一些激发态的普通粒子，它们质量极大，并不断地旋转和振动。接着，最右处是普朗克质量。在20世纪90年代早期，大多数物理学家们都期待，普朗克质量是基本粒子谱的终结。但是赫拉德·特霍夫特却持不同的观点。他认为一定有一些物体具有更大的质量。普朗克质量虽然在电子和夸克的质量尺度上看起来非常巨大，但其实也只不过与一小粒尘埃差不多重。显然，存在着许多更重的物体——保龄球、蒸汽机车头以及圣诞节水果蛋糕都是其中之一。但是在这些更重的物体中，给定质量下尺寸最小的那些是特殊的。

考虑一块质量大约是1千克的普通砖块，我们常说“如一块砖头一样坚硬”，即使砖块看起来很坚硬，但是实际上它们里面几乎是空的。给一个足够的压力，它们可以被压缩到一个更小的体积。如果压力足够大，一块砖能被压缩到一根大头针甚至是一个病毒那么小。但是它里面仍然几乎是空的。

但是存在着一个极限。我的意思并不是说，一个基于现在技术局限的实际操作上的极限。我讲的是自然规律和基本物理原理的极限。质量为1千克的物体所能占据的最小的直径是多少？普朗克尺度显然是一个猜想，但是它并不是正确的答案。一个质量为1千克的物体可以一直被压缩，直到它形成一个质量为1千克的黑洞^[195]。这时便再也无法压缩。对于一个给定的质量，这已经是可能存在的体积最小、密度最高的物体。

那么1千克的黑洞其尺寸有多小呢？答案可能要比你想象的还要小。这样一个黑洞的史瓦西半径（视界的半径）大约是1亿个普朗克长度^[196]。这个半径听起来很大，但是实际上只有单个质子的100亿分之一。它跟一个基本粒子差不多大小，所以为什么不能把它看成一个基本粒子呢？

特霍夫特就是这么做的。或者至少他说，它与基本粒子不会在任何一种重要的方式上，存在着本质上的不同。接着他提出了下面这个大胆的想法：

粒子谱并不会在普朗克质量终结。它会以黑洞的形式向着无限大的质量继续。

特霍夫特还认为，黑洞不应该有任意的质量值，应该像普通粒子一样，仅仅能取一些离散值。然而，这些可能的值，在普朗克质量上方如此稠密，间隔很近，看起来就像模糊的一片^[197]。

从普通物质（或者弦激发粒子）到黑洞的转化，并不是像我在图中所展示的那样界限分明。弦激发粒子极可能在普朗克质量附近变成了黑洞谱，两者之间没有任何明显的区别。这不是特霍夫特个人的猜测，正如我们将要看到的，我们确实有很好的理由相信它。

数弦和黑洞

爱丽丝的飞机是一个隐喻，隐约地指出了旁观者眼中所看到的会是什么样。爱丽丝从驾驶舱内看出去，在视界附近并没有看到任何异常的东西。但是从黑洞外面看过来，飞机似乎有越来越多的螺旋桨，慢慢布满整个视界。爱丽丝的飞机也可以用来比喻弦论是如何工作的。当一根弦掉向黑洞的时候，一个外部的观测者会看到弦上越来越多的部分显现出来，并慢慢占据整个视界。

黑洞的熵意味着黑洞有一个隐藏的微观子结构，这个结构与一浴缸热水中的水分子相似。但是就它自身而言，虽然熵可以提供一个关于视界原子数量的粗略计算，但是它并没有给出关于视界原子的本质的线索。

在爱丽丝的视界中，视界原子就是螺旋桨。也许真有一个量子引力的理论是基于螺旋桨的，但是我想弦论的观点更好一些，至少现在是如此。

关于弦有熵的想法，可以回溯到弦论的最早期。具体的细节很数学化，但是主要的想法很容易理解。我们先考虑一根最简单的弦，它代表了一个给定能量的基本粒子。更具体一点，我们假定其为光子。一个光子的在（或是不在）是1比特的信息。

但是现在我们对这个光子做一些处理。我们假定它就是一根很小的弦，摇动它、用其他弦撞击它或将它放入一个滚烫的煎锅上面^[198]。它开始振动、旋转以及伸展，就像一根小的橡皮筋。如果加入足够的能量，那么它就会变成一团巨大的乱麻：一个猫都能够抓住的纱线团。这不是量子晃动，而是热晃动。

一个缠结的纱线团不久变得极为复杂，很难描述其细节，但是我们仍然能得到一些粗略的信息。纱线的总长度可能是100码。这团乱纱线可能可以形成一个直径大约为6英尺的球。虽然没有给出细节，但是这种描述是有用的。这些未指明的细节就是隐藏信息，它们给出了这个弦球的熵。

能量和熵——听起来像关于热学的话题。实际上，一个由缠结的弦球所形成的处于极高激发态的基本粒子，是有温度的。这也是在弦论早期就已经知道的事情。这些缠结的被激发的弦，从很多方面上听起来很像黑洞。在1993年，我曾认真地考虑过黑洞会不会只是由一些巨大的随机纠缠在一起的弦形成的球状物，而不是别的什么东西。这个想法听起来很迷人，但是其细节则是完全错误的。

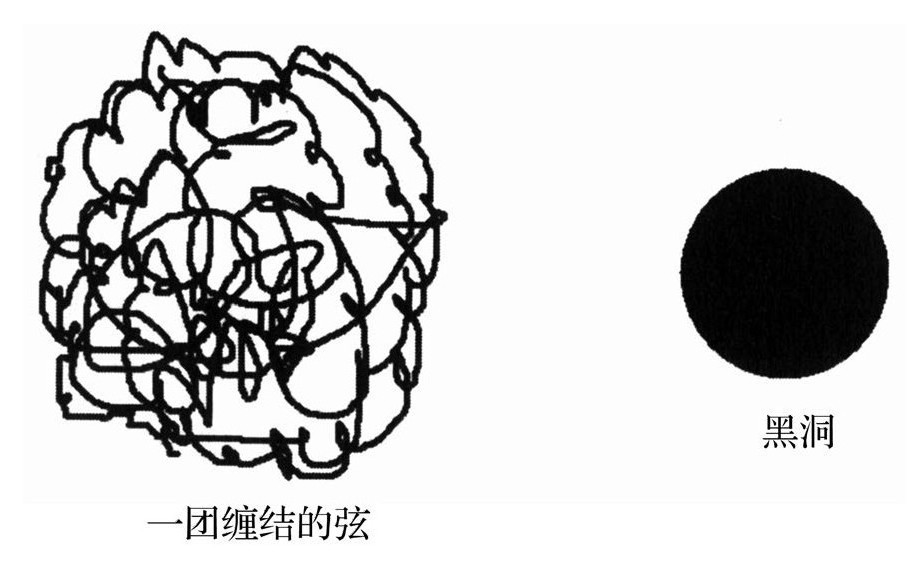
比方说，一根弦的质量（或者能量）与其长度成正比。如果1码长的纱线具有1克的质量，那么100码长的纱线则应该是100克，1000码长的纱线则是1000克。

但是一根弦的熵也与其长度成正比。设想在一根弦弯转和扭曲的地方沿其运动。每一次的弯转和扭曲都是几个比特的信息。一个简化的图像：假设弦就是晶格上面一系列刚性的联结，每一个联结要么是水平的，要么是垂直的。

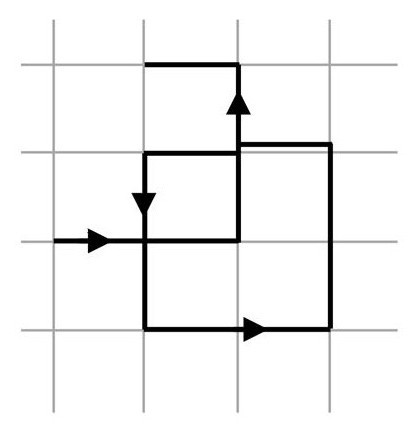
从一个单个联结开始，它可以向上、向下、向左或是向右，有着4种可能性，这等于2比特信息。现在加入一个联结。它可以在同一个方向上继续，向右转弯，或者180°转弯。这样就多了2比特。每一个新的连接都会增加2比特。这意味着隐藏的信息与弦的总长度成正比。

如果这团缠结的弦的质量和熵，都与其长度成正比，那么这就不需要用任何复杂巧妙的数学，即可证明熵是与质量成正比的。（“～”是正比例的数学记号）。

熵～质量

我们知道一个普通黑洞的熵是随其质量的增加而增加。但是对于黑洞来说，这种熵～质量特殊的关系并不正确。为什么呢？只要跟着正比例这根线索，我们就可以找出原因：熵与视界的面积成正比；面积正比于史瓦西半径的平方；史瓦西半径正比于质量。把它们结合起来看，你将看到熵并不正比于质量，而正比于黑洞质量的平方。

熵～质量平方

如果弦论是正确的，那么万物皆由弦构成的。万物指的是所有东西，应该包括黑洞。对此我很失望，倍感挫折，那是1993年夏天我所处的状况。

事实上，我傻透了。我错过了一些很明显的事情，但是直到那年的9月份我才发现它们，当时我去新泽西访问了一个月。美国最重要的理论物理研究中心中有两个在新泽西州，罗格斯大学和普林斯顿大学，它们相隔大约20英里。我打算在每个研究所都做一个报告，两个报告的名字都叫“弦论是如何解释黑洞熵的”。这个安排使我陷入了困境，我希望能在报告之前找出错误的地方。

我不知道我是不是唯一一个不断出现同一个噩梦的物理学家。在45年前我刚入行的时候开始，它就以各种形式出现。在梦里面，我要去做一个关于某些新研究的、很重要的报告，但是当报告越来越临近的时候，我却发现没什么好说的。我没做笔记，甚至不记得话题，压力和恐惧不断袭来。有时候我甚至发现自己穿着内衣站在听众前面，或者更糟，连内衣都没有穿。

这次不是做梦。两个报告中的第一个是在罗格斯大学。时间慢慢临近，我感到越来越大的压力，要把报告讲正确，确保它没有错误。那时只剩3天了，我意识到自己的愚蠢，我忽略了引力作用。

引力把物体拉在一起并压缩它们。我们以一块巨大的石头为例，比方说地球。没有引力，它可能仅仅是能把各部分黏在一块儿，就跟其他那些石头一样。但是引力有一个强大的效应，它把地球的各个部分都拽在一块，将核压缩到一个更小的尺寸。这种引力的吸引作用还有另一个效应：它将改变地球的质量。引力带有的这种负势能减少了地球的一部分质量。所以地球的实际质量要小于它各个部分的总和。

我应该停在这里，解释一下这个与直觉相悖的事实。我们回想一下可怜的西西弗斯，他一次又一次地把他的巨石推向山顶，然后又看着它滚落下来。能量转换的西西弗斯循环如下：

化学能→势能→动能→热能

不考虑化学能转换成势能的时刻（西西弗斯所吃的蜂蜜），从这块在山顶的巨石的势能开始算这个循环。尼亚加拉大瀑布中的水也具有势能^[199]，当物质掉到一个更低的高度时，势能就会变小。最终，它转换成了热能，但是热能以辐射形式进入了空间。所以净结果就是巨石和水在它们降低自己高度的时候失去了势能。

如果组成地球的物质（被引力）往地球的中心挤压，那么将会发生同样的事情：它失去了势能。丢失的势能以热能的形式出现，最终以辐射的形式射向了太空。由此推出：地球损耗了一部分净能量，所以也损失了一部分净质量。

因此，一旦引力作用被适当引入的话，我怀疑一根缠结的长弦其质量可能也会因为引力作用而减小，而不再与它的长度成正比。下面就是我设计的思想实验。假定有一个控制器可以用来逐渐调节引力的强弱。如果我们通过控制器单向地减小引力，那么地球将会变大也会变重。如果我们反向调节控制器增加引力，那么地球就会缩小而且变轻。如果再调大一些，引力会变得更强。最终会变得足够大以至于地球会坍缩成一个黑洞。最重要的是，黑洞的质量将会比地球的质量小很多。

我所假设的那个巨大的弦球，也会发生同样的事情。但是在之前思考弦球和黑洞间联系的时候，我忘了去开启引力控制器。所以在新泽西中部，一个没有其他事情可做的夜晚，我就开始思考如果打开引力控制器会怎样。在我想象的过程中，我可以看到弦球把自己压成一个密集的、缩小了的球。但更重要的是，我意识到这个新的、更小的弦球其质量比它开始的时候小很多。

还有一点。如果弦球的大小和质量变了，它的熵会变吗？幸运的是，当你缓慢调节控制器的时候，熵是严格不变的。这也许是熵的最基本事实：如果你缓慢地改变一个系统，能量可能会变化（以它通常的方式），但是熵还是保持不变。这个经典力学和量子力学的基础理论被称为绝热定理。

我们重新再做一遍这个思想实验，把地球换成一团巨大而混乱的弦。先将引力控制器调节到0。

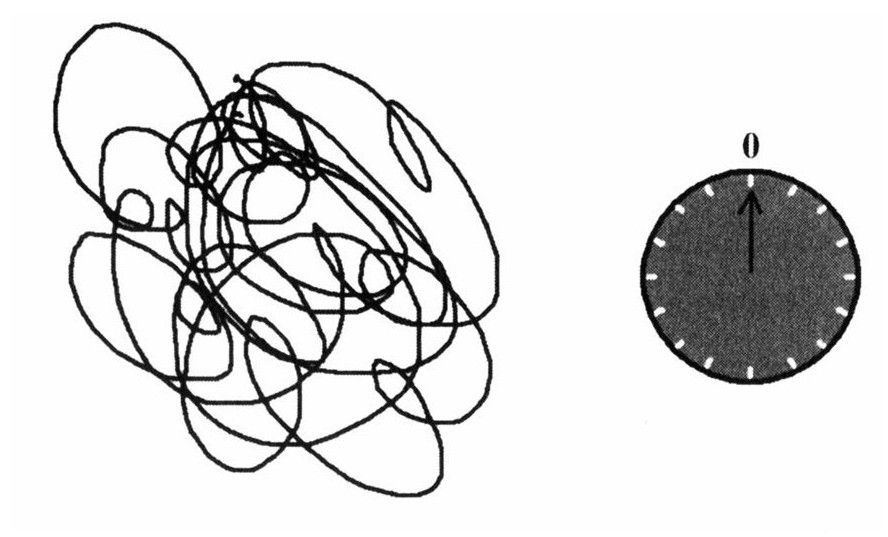
在没有引力的情况下，弦与黑洞并不相似，但它还是有熵和质量。接着，慢慢把引力调大。弦的各个部分开始相互拉拽，弦球开始收缩。

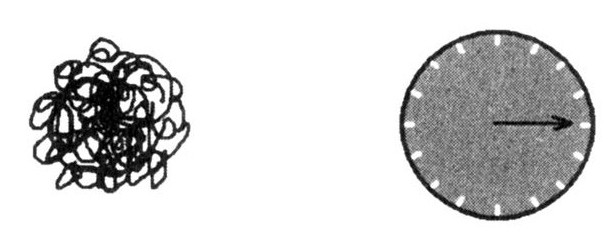
继续增大引力，这根弦将越变越紧，最终形成黑洞。

重要的是质量和大小都已经变小，但是它的熵并没有改变。如果我们把引力调回零又将发生什么？黑洞开始膨胀并最终变回一个巨大的弦球。如果我们缓慢地来回调节引力的大小，物体会在一个巨大的松散的弦球和一个紧致的黑洞间依次更替。但是只要我们慢慢地调节，熵还是保持不变。

在那时我突然顿悟了，意识到在关于黑洞的弦球图像的问题上出错的并不是熵。为了解释引力效应，质量必须要修正。我在一张纸上做了些计算，终于有了些头绪。当弦球收缩变成一个黑洞时，质量以某种特定的方式变化着。最后，熵和质量的关系为：熵～质量²。

但是这个计算并不完全，这很令人沮丧。记住那个小波浪形“～”意思是“成正比”，而不是“相等”。熵是否完全等于质量平方呢？还是等于质量平方的2倍呢？

黑洞视界呈现的图像是一团纠缠在一起的弦，通过引力作用平坦地贴附在视界面上。而我和费曼在1972年西区咖啡屋中，所想象的同样的量子扰动将导致弦上有些小片段会探出视界表面，而且这些小不点儿将成为那些神秘的视界原子。粗略地说就是，黑洞外的人将看到许多弦上的片段，其每一根的两端都牢牢地附在视界面上。在弦论的语言中，这些视界原子是附在某种胚上的开弦（有端点的弦）。实际上，这些弦上的片段可以从视界上掉出来，而且这可以解释一个黑洞是如何辐射和蒸发的。

看来约翰·惠勒是错了：黑洞是有毛发的。梦魇终于结束了，现在我的报告终于有东西可以讲了。

弦相遇的时候

基本弦可以相互穿越。下面的图就给了这样一个例子。设想一根你面前的弦远离你而去，而另一根离你较远的弦向你靠过来。它们会在某一点上相遇，如果它们是普通的蹦极绳，那么它们就会缠在一起。

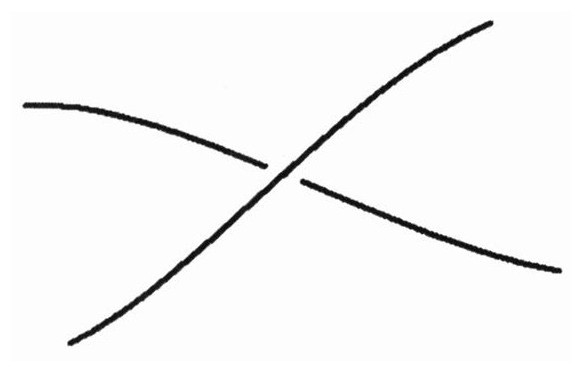
但是弦论的数学规则允许它们穿越彼此，而且以下一幅图所呈现的方式结束。

如果要对真实的蹦极绳做这些，你必须切断其中一根，然后在它们穿越后重新接上它。

在两根弦相互接触的时候还有另外的情况可能发生。除了相互穿越，它们还可以下图所示的方式重组它们自己。

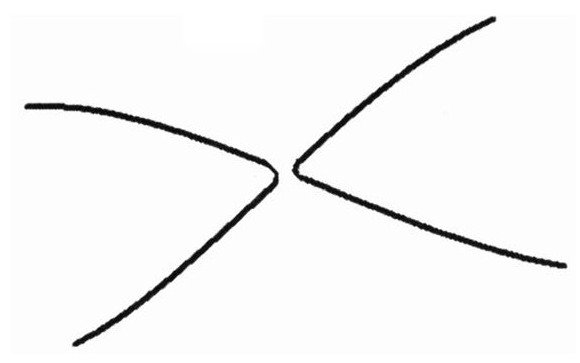
如果要在蹦极绳上实现这种方式，你需要将两根绳子都剪断，然后以这种新的方式重新连接。

当两根弦相互穿越的时候，穿越的方式是这两种中的哪一种呢？答案是有时候是这种，有时候是那种。基本弦是量子物体，在量子力学中没有任何东西是确定的——所有事情都是可能的，但是有确定的概率。例如，90%是穿越彼此，剩下的10%是它们重组。它们重组的概率被称为弦的耦合常数。

根据这个理论，我们集中来看在弦上的露在黑洞视界外面的一个小片段上。这个小片段被扭曲而且将要穿越它自己。

90%的情况下，它穿越它自己然后什么东西都没有发生。

但是10%的情况下，它可能会重组，而且当它重组时，一些新的东西就产生了。一个小弦圈脱落下来。

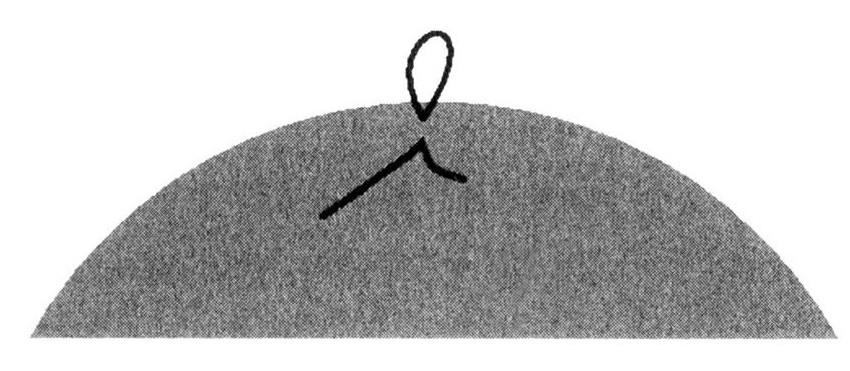
这个微小的闭合的片段就是一个粒子。它可以是一个光子、一个引力子或者任何其他粒子。因为它在黑洞的外部，所以它有机会逃逸，而且当它逃逸时，黑洞就会损失一部分的能量。弦论就是这样解释霍金辐射的。

回到新泽西

新泽西的物理学家们是一群思想锐利、极有主见的人。爱德华·威顿（Edward Witten），普林斯顿高等研究所的头号人物，不只是一位伟大的物理学家，还是一位全球首屈一指的数学家。有些人可能会说闲谈和空想并不是他所擅长的（虽然我发现他的冷幽默和广泛的好奇心非常有意思），但是每个人都会承认他思想的严谨是他最强的地方。我说的不是数学上那种没必要的严格性，而是清晰、认真、仔细思考过的论证。跟威顿谈论物理有时候很费劲，但却总是物有所值的。

在罗格斯大学的讨论和交流具有异乎寻常的高质量。在罗格斯大学有6位非常有成就的理论物理学家，他们中的每一个都深受敬仰，不仅在弦论圈中，在更为广泛的物理界亦是如此。他们都是我的朋友，其中有3个特别要好。我在汤姆·班克斯（Tom Banks）、史蒂夫·申克（Steve Shenker）和内森·“内蒂”·塞伯格（Nathan“Nati”Seiberg）还很年轻的时候就认识他们了，而且我很喜欢他们这个群体。这6个罗格斯大学的物理学家都有着令人生畏的智力。这两所研究所以严谨闻名，你休想带着那些尚未成熟的想法从那里逃脱。

现在，我知道我自己的论点，离完全成熟还很远。黑洞互补性原理，爱丽丝的飞机，用弦做的比喻，再结合一些粗糙的估算：我的图像就是将它们整合在一起。但是在1993年并没有什么工具能把这些想法变成严格数学。然而，我所坚持的这些想法却与新泽西那些强势的物理学家们，产生了共鸣。特别是威顿的反应，他或多或少直接接受了这个关于黑洞视界的假设，即，黑洞视界是由一些弦的片段所构成。他甚至算出了弦是如何在一个类似黑洞蒸发的方式中蒸发的。申克、班克斯和他们的伙伴迈克尔·道格拉斯都为如何精确化这些想法，提出了非常有用的建议。

其中有一位在那里做访问的弦论学家，我并不太熟悉。康朗·瓦法（Cumrun Vafa），一个哈佛的年轻教授，从伊朗跑到美国来普林斯顿研究物理。1993年的时候，他被认为是世界上最具创造力和数学技巧的理论物理学家之一。虽然主要是研究弦论，但是他对黑洞物理也颇具造诣，当我在罗格斯大学解释熵是如何在一个具有弦结构的视界上产生的时候，他也是听众之一。我们随后的谈话是具有决定性意义的。

极端黑洞

我在报告中说道，如果一个电子掉入黑洞中，这个黑洞将带电，这点大家都明白。这个电荷很快地遍及视界，并将导致一种排斥作用，把视界略微往外推出一点。

但是并没有理由放一个电子就停下来。你想让视界带多少电荷，视界就能带多少电荷。你让它带的电荷越多，视界向外移动得就越多。

康朗·瓦法指出有一种非常特殊的带电黑洞，其引力的吸引作用和电的排斥作用正好相平衡。这种黑洞被称为是极端的。根据瓦法所说的，极端黑洞将会是一个理想的实验室，可用来检验我的想法。他认为它们可能是一把通向精确计算的钥匙，那里宽松的正比记号（～）将被坚实的等号（=）所取代。

让我们更深入地了解一下这个带电黑洞的想法。荷电球通常是不稳定的。因为电子相互排斥（记住规则：同性相斥，异性相吸），如果一个电荷云恰巧形成，它通常会马上被电的排斥力撕裂。但是如果电荷球质量足够大，引力便可以抵消电所产生的排斥力。因为宇宙中所有东西都会因引力而相互吸引，这就会出现一个引力和电力的竞赛——引力把电荷拉到一起而电力把它们推开。一个带电的黑洞是一场拔河比赛。

如果荷电球质量很大，而所带的电荷很少的话，引力将赢得这场拔河比赛，该球将收缩。如果质量很小而带的电量很大，那么电排斥力将会获胜，该球将膨胀。当电荷和质量处于某种合适的比例时，它们将达到平衡。这时，电的排斥力和引力相互平衡，这场拔河比赛将成为平局。这就是极端黑洞。

现在设想我们有两个控制器，一个是引力的，一个是电力的。起初，把两个控制器都打开。当引力和电力处于完全平衡时，我们就会得到一个极端黑洞。倘若我们减小引力而不减小电力，那么电力将会赢得这场拔河比赛。但是，如果我们按一定比例同时减小它们，那么这种平衡将持续下去。每一边都在变小，而任何一边都不会占得优势。

如果我们最终把控制器都调到0，那么引力和电力都消失了。剩下的是什么呢？一根各个部分之间没有相互作用的弦。在整个过程中，熵是不变的。但是故事的高潮是质量居然也没有变化。这两个电力和引力相互抵消，没有起什么作用，这是一个用技术化的方式来说明，能量始终保持着它开始时的量。

瓦法认为如果我们知道如何在弦论中构造这些极端黑洞，那么我们就能以很高的精度来研究其在引力和电力变化时的情况。他说这应该是可行的：利用弦论，来精确地计算那个数值因子。对于这一点，我完全没有能力去计算。为了将所有想法结合起来，精确地计算数值因子成了弦论学家追逐的圣杯^[200]，也是实现我想法的一条途径。但是没有人知道，如何用弦论所提供的配件，去组装一类合适的带电黑洞。

弦论有点像一套非常复杂的装配式玩具^[201]，带有许多不同的零件，这些零件可以通过某种自洽的模式拼凑在一起。后面我将告诉你们一些这种数学上的“轮子和齿轮”，但是在1993年用来铸造极端黑洞的一些重要的零件还没有被发现。

印度物理学家阿肖克·森（Ashoke Sen）是第一个尝试组装极端黑洞并检验黑洞熵的弦论理论的人。在1994年他已经非常接近了，但是还不足以完成这件事情。在理论物理学家中，森的地位很高。他是一位深刻的思想家，也是一个技巧上的奇才。森是一位害羞而带着很重孟加拉口音的小个子，他的讲演以思路清晰闻名。他用完美的教法论技术，在黑板上写下每一个新的概念。每一个概念在他的讲述下都像水晶一样清澈，这也是他一贯的风格。他的学术论文也有着同样的清晰度。

我并不知道森正在做一些黑洞的工作。但是在我结束剑桥的旅行，返回美国后不久，有人——我记得是阿曼达·佩特——给了我一份他正在读的论文。这是一篇技术性的长文章，但是在最后的几段中，森用了弦论的想法，就是我在罗格斯大学上描述的那些，来计算一类新型的极端黑洞的熵。

森的黑洞是由我们在1993年所了解的一些零件所组成——基本弦和6个额外空间维。森接下去做的事情很简单，但是非常聪明，发展了我早期的一些想法。他基本的想法就是考虑一根处于极高激发态的弦，而且这根弦在一个紧致方向上缠绕了许多圈。在这个简化的柱面世界中——线地的增粗版本——一根缠绕着柱面的弦就像是一根被套在塑料管子上面的橡皮筋。

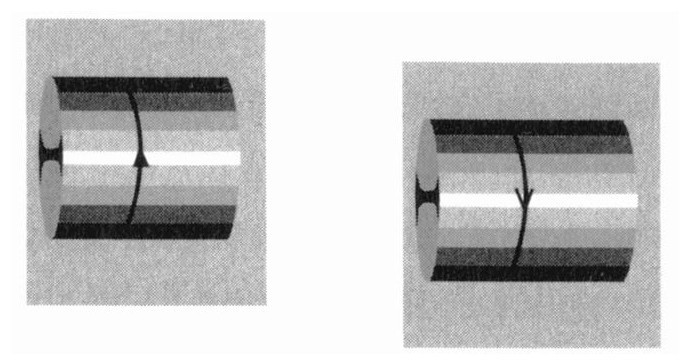
这样的弦比普通的粒子要重一些，因为它需要能量来缠绕在柱面上。在典型的弦理论中，这根缠绕着柱面的弦其质量可能比普朗克质量大几个百分点。

接着森用单根弦在柱面上缠绕两圈。

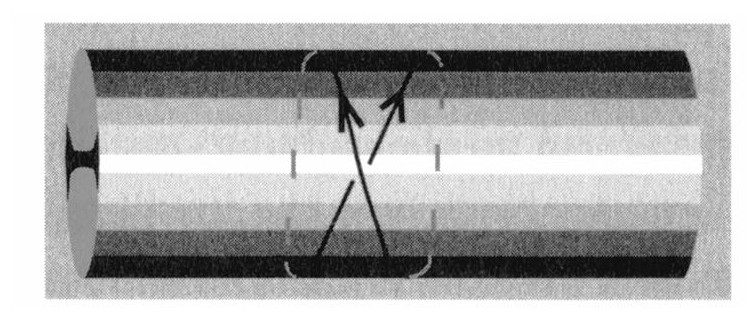
如果一个弦论学家说这根弦的绕数是2，那么这根弦要比缠绕一次的弦来得重。但是如果弦在这个紧致的方向上缠绕不是一次、两次而是数十亿次会怎样呢？

没有极限限定弦在这个紧致的空间方向上能绕多少次。最终，它将变成一个跟恒星甚至星系一样重的东西。但是它所占据普通的空间——普通的非紧致的三维空间——很小。所有的质量都被禁锢在如此小的一个空间中，那么一定会形成黑洞。

森还用了一个技巧：沿着弦摆动，而它就是1993年前后弦论中剩下的那个配件。正如我一年前所说的那样，信息被隐藏在摆动的细节中了。

一根具有弹性的弦上面的摆动并不是固定不变的。它们沿着弦运动就像波一样，有一些顺时针移动，有一些逆时针移动。两个摆动朝着同方向沿着弦互相追逐并不相撞。然而，如果两个波以相反方向移动，那么它们必将相撞，情况就会变得非常混乱和复杂。所以森选择用步伐一致的不会相撞的顺时针波，来储存所有隐藏的信息。

当所有零部件被装配起来，各个控制器被开启，森的弦没有其他的选择，只能变成黑洞。但是不同于普通的黑洞，在环形紧致方向上的绕缠使得这类极端黑洞非常特殊。

极端黑洞是带电的。那么电荷在哪里？答案已经知道好多年了：在一个紧致方向上缠绕一根弦会带来电荷。每绕一圈就会带来一个单元的电荷。如果弦是朝一个方向绕转，那么它带正电；如果它朝另一个方向绕转，那么它将带负电。森的那些巨大的绕法多样的弦，可以看做是由引力聚在一起的一个荷电球——换句话说就是一个带电黑洞。

面积是一个几何概念，时空的几何是由爱因斯坦的广义相对论所决定的。唯一能知道黑洞视界面积的方式，就是用爱因斯坦引力方程计算它。森，一个解方程的大师，很轻松地解出了这个关于他造出来的特殊黑洞的方程，并计算了视界的面积。

灾难！当方程被解出，视界面积被求出后，答案居然是零！换句话说，视界缩小到了仅仅是一个空间点，而不是一个巨大的球壳。所有的熵都被储存在那些摆动中，像蛇一样的弦似乎集中到了一个极小的空间点中。这不仅仅是黑洞的麻烦，它也与全息原理有着直接的矛盾：一个空间区域的最大的熵就是它以普朗克单元为单位的面积。一定是什么地方出错了。

森很清楚地知道哪里出了问题。爱因斯坦方程是经典的，这意味着他们忽略了量子扰动。除去量子扰动，在氢原子中的电子会掉向原子核，而整个原子的大小不会超过一个质子。但是由不确定性原理导致的量子的零点运动使得原子要比原子核大10 000倍。森意识到同样的问题可能发生在视界上。虽然经典物理预言它将收缩成一个点，但是量子扰动将使它膨胀到我所说的一个延伸视界。

森做了必要的修正：他粗略地估算了一下，发现熵和延伸视界的面积确实是成正比的。这是弦论关于视界熵的另一次胜利，但是如以往那样，这次胜利并不完全。我们仍离目标很远，还是不能精确地确定量子扰动会使视界延展多少。虽然森的工作是那么的出色，但是仍然只能以一个宽松的“～”结束。森最多也只能说，黑洞的熵是与视界的面积成正比的。虽然已经很接近了，但是仍然没有拿到那根最后的钉子。那个“盖棺定论”的计算还没有做。

这类差不多的计算是不可能说服史蒂芬·霍金的，它们的胜算并不会比我的论证高。然而，完整的结果正在接近。根据瓦法的提议，制造一个巨大经典视界的极端黑洞，需要一些新的装配部件。幸运的是，这些必要的零件将在圣芭芭拉被发现。

波尔钦斯基的D-胚

D-胚应该被称为是P-胚，这里的P就是波尔钦斯基（Polchinski）的首字母^[202]。但是在波尔钦斯基发现这个胚的时候，P-胚这个术语已经被用在了一个不相关的东西上了。所以波尔钦斯基就用19世纪德国数学家约翰·狄利克雷（Johann Dirichlet）的名字给它们命名，称它们为D-胚。狄利克雷与D-胚并不直接相关，但是与他关于波的数学研究相关。

英语“胚”（brane）这个词在字典中并不存在，只在弦论中使用。它来自一个普通的单词——膜（membrane），一个可以延伸、可以弯曲的二维曲面。波尔钦斯基1995年关于D-胚的发现，是近年来物理学上最重要的事件之一。它不久就对从黑洞到核物理的所有东西，都产生了深远的影响。

最简单的胚是0维的，被称为0-胚。一个粒子或是一个空间点是0维的，因为在一个点上面没有地方可以移动，所以粒子和0-胚是同义词。我们升高一维，来看1-胚，它是1维的。一根基本弦就是1-胚的一个例子。膜——2维的物质面——是2-胚。那么3-胚呢——有这样的东西吗？想象一块橡皮的立方体充满了一个空间区域。你可以称其为充满空间的3-胚。

我们似乎有点偏离了方向。很明显，我们没有办法把一个4-胚填入3维的空间中。但是如果空间具有紧致维呢——例如有6个紧致维呢？在这种情况中，4-胚中的一个方向可以沿着紧致方向延伸。实际上，如果总共有9维，那么空间可以是9维以及9维以下的任意维度。

一个D-胚不仅仅是一种胚，它有一个非常特殊的特性——基本弦可以在上面终结。考虑D0-胚的情况。D意味着是一个D-胚，而0意味着是0维的。所以D0-胚是一个基本弦可以在其上终结的粒子。

D1-胚通常被称为是D-弦。这是因为一个D1-胚是1维的，它自身就是一种弦，虽然我们不应该将它和基本弦搞混^[203]。一般来说，D-弦要比基本弦重得多。D2-胚是膜，类似于橡皮纸，但是，同样具有基本弦可以在上面终结的特性。

D-胚只是一个波尔钦斯基在弦论中添加的一个随意的奇想？仅仅是因为他觉得可以那么做？我想，在他开始的一些探索工作中可能是这样的。理论物理学家常常会发明一些新的概念只是为了摆弄摆弄它们，看看它们能导出什么结果。实际上，1994年波尔钦斯基第一次向我展示D-胚这个概念的时候，讨论的真正精神是：“看，我们可以在弦论里面加一些新的东西。这不是很好玩吗？我们可以研究一下它们的特性。”

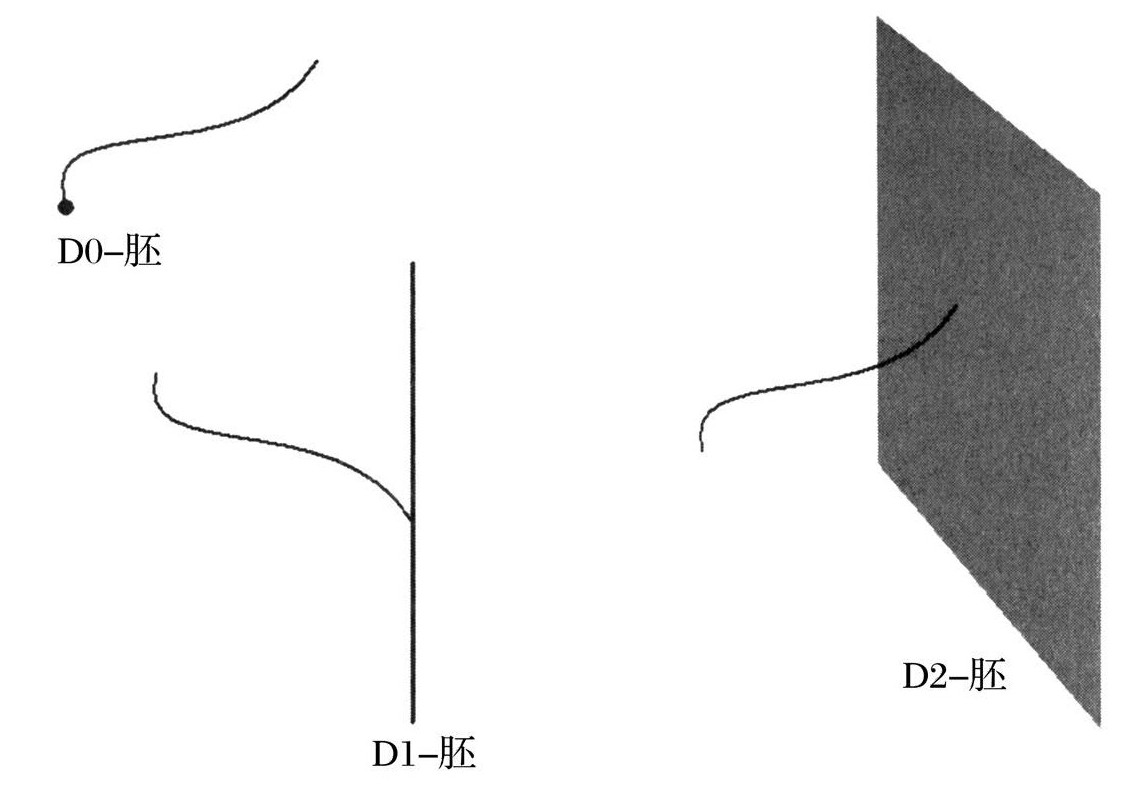
但是在1995年的某个时候，波尔钦斯基意识到D-胚弥补了弦论在数学上的一个很大的漏洞。实际上，它们的存在是一个必要补充，使不断扩大的逻辑和数学网络得以改进。为了构造一个更好的极端黑洞，D-胚是所需要的那个缺失的神秘零件。

取得成功的弦论数学

在1996年，瓦法和安迪·斯特鲁明格突然发动了袭击。通过结合弦和D-胚，他们可以构造出一个带有较大且明确经典视界的极端黑洞。因为一个极端黑洞被认为是一个大型的经典物体，量子晃动只有在视界上面才有一些不可忽视的效应。现在没有了摆动，弦论可以更好地给出霍金公式中所蕴藏着的隐藏信息的总量，而且没有不确定的因子2或者是π，也没有正比记号。

这并不是你那类基础的传统黑洞。这个斯特鲁明格和瓦法用弦和D-胚所构建的黑洞，听起来像一个精心安排的梦魇，但是它是人们所寻找的大型经典视界中最简单的结构。所有弦论的数学技巧都被用上了，包括全部的额外维、弦、D-胚、还有许多其他的技巧。首先，这些弦被嵌在许多D5-胚上，这些胚撑满了6个空间紧致方向中的5个。除了被嵌入在D5-胚上，它们还在其中一个紧致方向上，缠绕了大量的D1-胚。然后它们增加弦的数量，弦的两头都被按在D-胚上面。又一次，弦上那些露出来的片段将变为包含着熵的视界原子。（如果你有一点迷糊的话，不要担心。我们进入了一个新领域，人类大脑无法轻易重新装备的领域。）

斯特鲁明格和瓦法沿用了他们早先用过的步骤。首先，他们将控制器读数调到0，这样引力和其他作用力将会消失。没有了这些力的干扰，我们可以精确计算在开弦的扰动中能储存多少熵。这些技巧性很高的计算要比以往任何东西都要来得复杂而精妙，但是他们施展了数学绝技，成功了。

下一个步骤就是解这类极端黑洞的爱因斯坦场方程。计算这个面积并不需要不确定的伸展步骤。正如我与大家共同所愿，斯特鲁明格和瓦法发现视界的面积和熵并不仅仅是成正比的；那些黏在胚上的弦，其上的摆动中所隐藏的信息，与霍金的公式完全一致。他们已经找到了它。

就如以往常发生的那样，几乎同时，有好几组人突然想出同一个新的想法。斯特鲁明格和瓦法在做他们的工作的同时，最聪明的新一代物理学家中的一个，当时还只是一个普林斯顿的学生，胡安·马尔达西纳（Juan Maldacena）完成了他的学位论文。胡安·马尔达西纳的博士论文的导师是柯特·卡兰（CGHS中的C）。马尔达西纳和卡兰也将D5-胚和D1-胚以及开弦结合。在几个星期中，斯特鲁明格和瓦法，卡兰和马尔达西纳各自发表了他们的论文。他们的方法不太一样，但是他们的结论完全证实了斯特鲁明格和瓦法所说的。

事实上，卡兰和马尔达西纳能够在先前的工作上走得更远一些，而且还可以计算准极端黑洞。一个极端黑洞在物理上是很奇怪的一个东西。它是一个带有熵的物体，但是没有热能，没有温度。在大部分的量子力学的体系中，一旦所有能量都被抽走，那么一切东西都被牢牢地钉在了位置上。例如，如果把一块冰块的所有热能都抽走的话，那剩下的将是一块完美的不带有任何瑕疵的水晶。任何水分子的重新分布都需要能量，所以重新分布会增加热能。所有热能都被抽走后的冰，不含过剩的能量，没有温度，没有熵。

但是也有例外。某些特殊的系统有许多能量取相同最低值的状态。换句话说，即便是所有的能量被抽走后，仍有许多种重组系统的方式来隐藏信息，并且这不增加能量。物理学家们说这些系统有着退化的基态。带有退化基态的系统具有熵——它们可以隐藏信息——甚至是在绝对零度。极端黑洞是这些特殊的系统的一个理想的例子。不像普通的史瓦西黑洞，它们处于绝对零度的时候，就意味着它们不蒸发。

我们回到森的例子中。在这种情况下，弦上的摆动都朝着一个方向运动，因此它们不会相互撞击。但是假设我们加一些反方向运动的摆动。如你所预期的，它们与原来的那些摆动相撞并制造了一些混乱。实际上，它们加热了弦，提高了温度。不像普通的黑洞，这些准极端黑洞不会完全地蒸发，它们把它们过剩的能量排出去，并回到极端的状态。

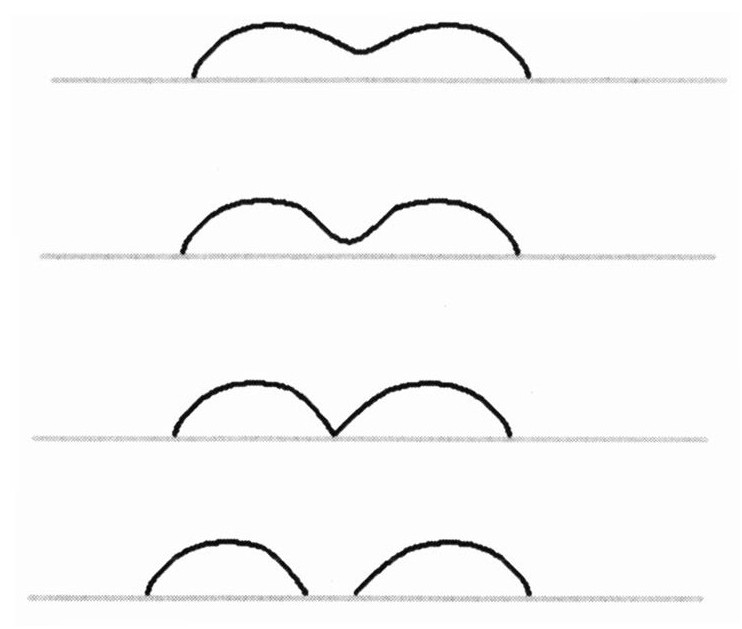
卡兰和马尔达西纳能用弦论来计算准极端黑洞蒸发的速率。弦论用来解释蒸发过程的方式是令人着迷的。当两个摆动朝着两个相反的方向移动并相撞时，如下图：

它们会形成一个单个的，更大的摆动，看起来就像这样：

一旦这个更大的摆动形成，便没有东西可以制止它脱离出来，粗略看起来，这与我和费曼在1972年所讨论的东西没什么不一样的。

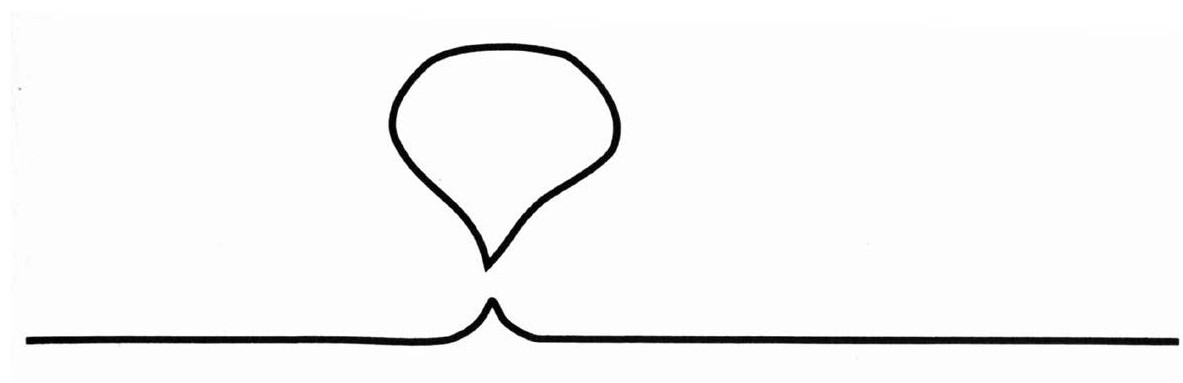
但是卡兰和马尔达西纳所做的东西，要比与费曼那次谈话来得多。他们对蒸发的速率做了非常具体的计算。令人吃惊的是，他们的结果与用霍金20岁时的方法所得到的结果完全一致，只有一个重要的区别：马尔达西纳和卡兰所做的只是用了传统的量子力学的方法。如我们在前面章节中所讨论的，尽管量子力学是以统计为基础的，但是它并不允许信息丢失。因此，没有可能信息会在蒸发过程中丢失。

而且，其他人也有相似的想法。来自孟买Tata研究所（也是阿肖克·森所在的研究所）的两组完全独立的印度物理学家——素密·达斯（Sumit Das）和萨米尔·马图尔（Samir Mathur），以及高塔姆·曼达尔（Gautam Mandal）和斯彭达·瓦迪亚（Spenta Wadia）——也做了一些类似的计算。

总的来看，这些工作取得了巨大的成功，而且它们都实至名归的。黑洞熵可以通过储存在弦上摆动中的信息来解释，这个事实与包括霍金在内的许多相对论学家的观点冲突。霍金把黑洞看成是一个吞噬信息的东西，而不是一个储存信息的容器。斯特鲁明格—瓦法的计算成功证明了一个数学结果可以改变天平的倾向。这是信息丢失终场一幕的开场。

人们都注意到了这戏剧性的一幕。许多人包括我在圣芭芭拉的那些朋友，都突然跳上了我们的船，背叛了另一派。如果我先前觉得这场黑洞战争可能会打成平手，那么当乔·波尔钦斯基和加里·霍洛维茨——以前他们在这场战争中是中立的——变成我的盟友时^[204]，这些怀疑就烟消云散了。在我的印象中，这是一个分水岭。

弦论可能是自然界的正确理论，也可能不是，但是它证明了霍金的论证是错误的。把戏已被拆穿了^[205]。但是令人吃惊的是，霍金和许多广义相对论界的学者还是不肯就此罢休。他们继续被霍金早年的论证所蒙蔽。

第22章　南美赢得胜利

如果要罗列一批杰出的物理学家，大部分人并不会想到南美洲。甚至连南美洲人自己都不太相信有那么多著名的理论物理学家来自阿根廷、巴西和智利。达尼埃莱·阿马蒂（Daniele Amati）、阿尔贝托·希林（Alberto Sirlin）、米格尔·维拉索罗（Miguel Virsasoro）、黑克托尔·鲁宾斯坦（Hector Rubinstein）、爱德华多·弗拉德金（Eduardo Fradkin）和克劳迪奥·泰特尔鲍姆（Claudio Teitelboim），这仅仅是一些在这个领域中有重要影响的人物。

泰特尔鲍姆最近把名字改成了克劳迪奥·本斯特（Claudio Bunster）（参看第8章有关脚注）。他是一个非同一般的人物，跟任何其他我所知道的物理学家都不一样。他的家庭与智利社会党主席萨尔瓦多·阿连德（Salvador Allende）以及诗人、社会活动家^[206]、诺贝尔奖得主巴勃罗·聂鲁达（Pablo Neruda）有着非常紧密的关系^[207]。泰特尔鲍姆的兄弟，塞萨尔·本斯特（Cesar Bunster）是1986年9月7日行刺前法西斯独裁者奥古斯托·皮诺切特（Augusto Pinochet）将军的领头人^[208]。

泰特尔鲍姆身材高大，皮肤黝黑，体魄强健，双目炯炯有神。尽管有一点结巴，但是他有着一个伟大的政治领袖的魅力和潜在感召力。事实上，他就是一个科学家小团体中的反法西斯领袖，确保了科学能在智利的那些黑暗岁月中存活下来。我确信他在那个时代处境很危险。

泰特尔鲍姆能力极强，也有一点点疯狂。虽然他是智利军方的敌人，但是他却迷恋着各种军品。在回智利之前，他生活在得克萨斯，会常常去参观那些刀和枪的展览，甚至在今天他也常常穿着军装。我第一次去智利看望他时，他打扮成士兵的样子，把我吓得魂不附体。

那是1989年，皮诺切特的独裁政治还处于鼎盛时期。当我和我的妻子，以及我的朋友威利·菲施勒，在圣地亚哥下飞机时，我们被粗鲁地赶进了一条很长的等待护照检查的队伍。排在这条队伍中的都是些配备着重型武装，穿着军队制服的士兵。入境检查的工作人员是全副武装的军人，其中一些带着大型自动化武器。完成入境检查不是一件容易的事情：这条长长的队伍似乎一动不动，而我们已经是筋疲力尽了。

突然，我看到一个戴着太阳眼镜穿着一身军装的高个子（或者是那种被看作军装的衣服）冲过封锁区径直地奔向我们。是泰特尔鲍姆，他正在给士兵们下达命令，看起来好像是一个将军。

当他走到我们跟前时，他抓住我的手臂并骄傲地护卫我们穿过卫队，并以一种非常威严的态度向士兵们挥手示意，要求他们让道。他抓住我们的行李，并快速地带我们离开了机场，走向他那辆非法停靠的土黄色吉普车。然后我们极速驶离机场，开进了圣地亚哥，拐弯时车的两个轮子都离地了。每当有士兵经过我们身边时，泰特尔鲍姆都会鸣笛致敬。“泰特尔鲍姆，”我低声地说，“你为什么弄出哗哗声？你会让我们都死掉的。”但是没有人把我们拦下来。

我最后一次在智利的时候^[209]，皮诺切特时代已被一个民主政府所取代，泰特尔鲍姆与军队有了真正的联系，特别是空军。那是泰特尔鲍姆在他的小研究所内举办的一次关于黑洞的会议。他动用了他在空军的影响力，把我们其中的一些人，包括我和霍金，用飞机接到了智利的南极基地。我们在那里过得很愉快，但是令人印象最深的事情就是空军将军们招呼我们的方式，其中也包括他们的首长。一个将军倒茶，另一个递上开胃食品。泰特尔鲍姆在智利显然是一个很具影响力的人物。

但正是在1989年，在去往智利安第斯山脉的一辆旅行巴士上，泰特尔鲍姆第一次告诉我了某种反德西特黑洞。今天，它们被称作BTZ黑洞，意思为巴纳多斯—泰特尔鲍姆扎—内利黑洞。马克斯·巴纳多斯（Max Banados）和若热·扎内利（Jorge Zanelli）是泰特尔鲍姆的亲密伙伴，他们三个的发现，在黑洞战争中产生了深远的影响。

天使与魔鬼

黑洞物理学家们永远喜欢把一个黑洞封装在一个盒子里，并像保护珍贵的宝石一样保护它。是为了防止什么呢？防止蒸发。把它封装在一个盒子里就像给一壶水盖上盖子。粒子将会在盒子的各个盒壁间（或是水壶的盖子）不断反弹，并回到黑洞（或水壶）而不会被蒸发到外部空间。

当然，没有人真会把一个黑洞放入一个盒子中，但是这个思想实验却蛮有意思。一个稳定的、不变的黑洞，将比那些蒸发的黑洞简单得多。但是会出现一个问题：没有真实的盒子可以永远包裹黑洞。就像其他任何东西一样，真实的盒子是有随机晃动的，而且迟早会有意外发生。这个盒子将会与黑洞产生某种联系，而最终被黑洞吞没。

这时反德西特（AdS）空间出现了。首先，不管它的名字是什么，反德西特空间确实是一个时空连续统，其维度中包含着时间维。威廉·德西特（Willem de Sitter）是一个荷兰的物理学家、数学家和天文学家，他发现了爱因斯坦方程的一个4维解，并用他的名字命名了这个解。数学上，德西特空间是一个以指数式膨胀的宇宙，其膨胀方式与我们的宇宙很相似^[210]。德西特空间是一个很久以前的想法，而不是一个什么新鲜的东西，但是近年来，它对于宇宙学家来说却极为重要。它是一个带有正曲率的弯曲的时空连续统，这意味着三角内角之和大于180°。但是所有这些都不是重点。在这次讨论中，我们感兴趣的是反德西特空间，而不是德西特空间。

反德西特空间并不是德西特的反物质双胞胎兄弟发现的。“反”表示空间曲率是负的，意味着内角之和小于180°。关于AdS最有意思的事情，就是它有着许多球状盒子内壁的特性，一个不能被一个黑洞吞噬的盒子。这是因为AdS的球状墙面对于任何靠近它的东西都会施加一个强大的作用力——一个不可抗拒的排斥力，其中也包括黑洞的视界。这种排斥力足够强，以至于墙面和黑洞之间不可能产生任何联系。

总的来说，普通的时空有4个维度：3个空间维和1个时间维。物理学家们有时候称之为4维，但是这样却模糊了空间和时间之间的明显的不同。一个关于时空的更加精确的描述就是（3+1）维。

平地和线地都是时空连续统。平地是一个仅有2个空间维的世界，但是居住在上面的人，也会感觉到时间。他们会很正确地将自己的世界称为（2+1）维。线地人生活在（1+1）维的时空中，他们只能够在一根轴线上移动，但是他们也是能够感觉到时间。（2+1）维和（1+1）维的好处就是能够容易地画出它们的图像来帮助我们的直觉想象。

当然，没有什么可以阻止数学物理学家去创造一个带有任意空间维的世界，虽然大脑没有能力看到这些维度。有人可能会想，有没有可能可以更改时间维度的数量。在一个完全抽象的数学感觉中，这个答案当然是肯定的，但是如果从物理学家的观点来看，这似乎没有什么意义。时空维数是单一的一维看起来是正确的。

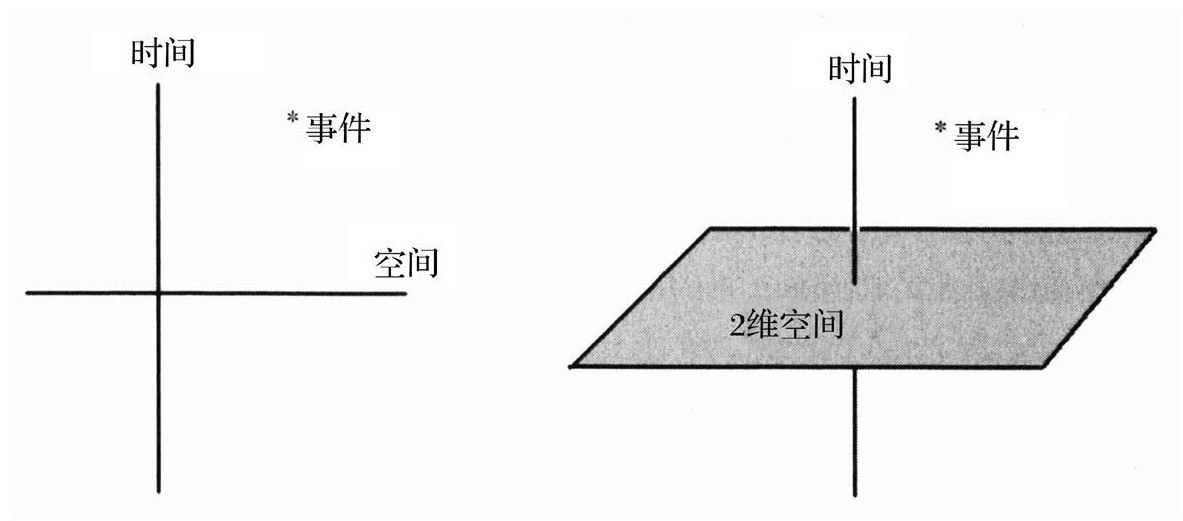
（1+1）维时空　　　　　（2+1）维时空

反德西特空间也有多种维度。它可以有任意数目的空间方向，但是只有一个时间方向。巴纳多斯、泰特尔鲍姆和扎内利所研究的AdS空间是（2+1）维的，这使得用图来解释变得比较容易。

不同维度上的物理

三维空间（不是时空）在我们的认知中似乎是根深蒂固的。没有人可以不借助于抽象数学的帮助，想象出四维空间。你可能会认为一维或二维的空间比较容易构造图像，而且某种意义上确实如此。但是如果你再想一会儿，你就会意识到当你在想象线和平面的时候，你总是在认为它们是嵌入三维空间的。这当然是我们大脑进化的方式的缘故，与任何特殊的三维数学特性无关。^[211]

量子场论，基本粒子的理论，在一个维数较低的世界中跟它在三维空间中一样成立。我们所能说的，基本粒子完全有可能是在二维空间（平地）甚至是一维空间（线地）的。事实上，在维数减少后，量子场论的方程要简单一些，而且这个领域中我们所知道的许多东西，首先是在这些世界模型的量子场论研究中发现的。所以巴纳多斯、泰特尔鲍姆和扎内利它们研究一个空间维数只有2的宇宙没有什么奇怪的。

反德西特空间

解释AdS的最好的方式，就是用泰特尔鲍姆在智利的旅行巴士上所用的方式：用图。我们先忽略时间，并从一个空圆盒子中的普通空间开始。在三维中，一个球形的盒子意味着内部是一个球；在二维中，这甚至更加简单，内部就是一个圆。

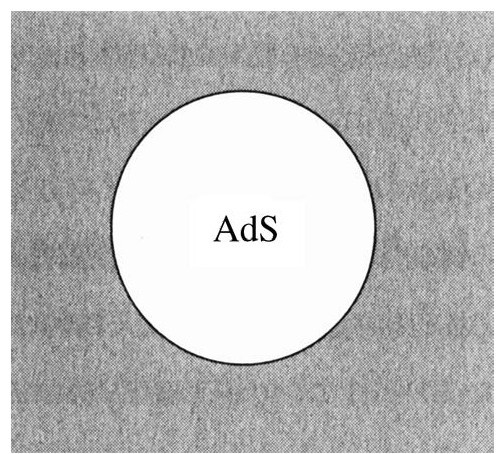
现在我们加入时间维。我们用竖轴表示时间，盒子里面的时空连续统类似于一个柱体的内部。在下面的图中，AdS就是柱体中没画上阴影的内部。

想象一下给AdS切片（记住，它只有一个时间维），方式与我们给黑洞切片构成一个嵌入图相同。真正能称为空间的，是切出来的空间性截面。

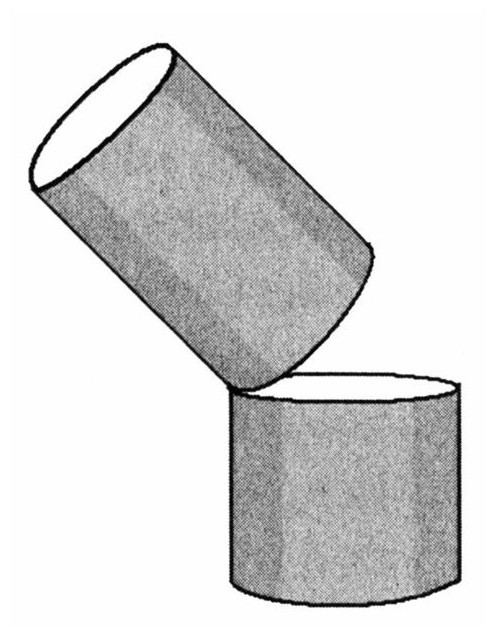
我们再仔细检查一下这个二维片层，如你所期望的，它是弯曲的，就像地球的表面一样。这意味着如果要在一个平面上画出它，你必须要延展和弯曲这个曲面。我们不可能不失真地在一张平的纸上画出这幅地图。在一幅麦卡托地图上，靠近北部和南部的边缘上的区域看起来就要比赤道附近的区域大很多^[212]。格陵兰岛看起来就像非洲那么大，尽管它的面积只有非洲面积的1/15。

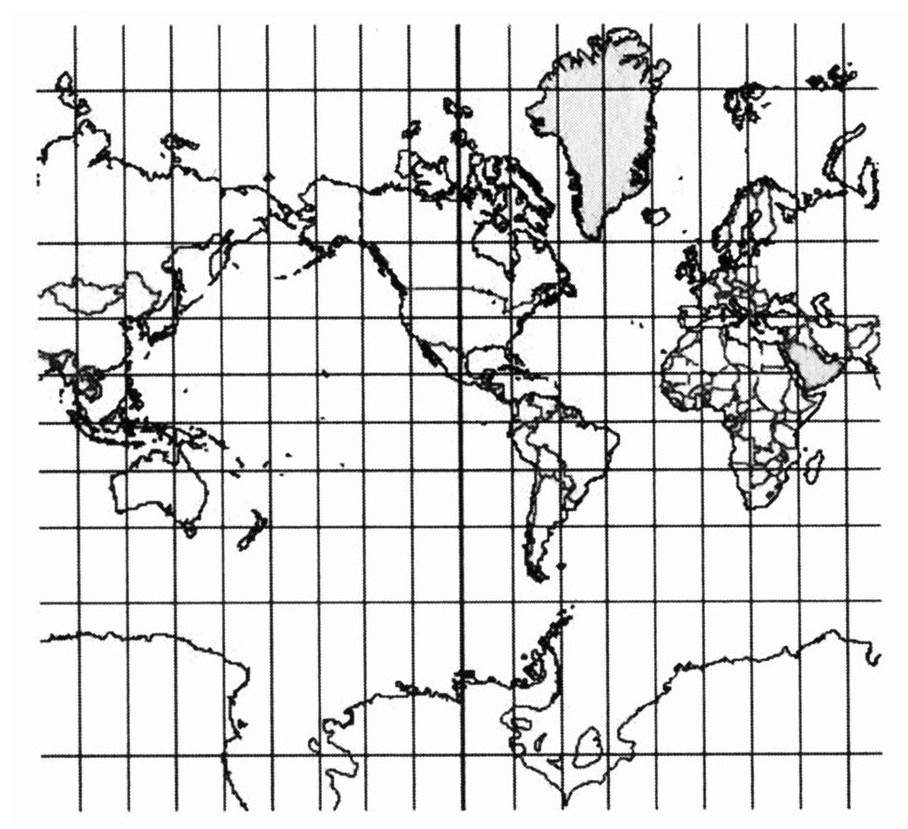
AdS中的空间（或者时空）是弯曲的，但不像地球的表面，它们的曲率是负的。如果将它们平展到一个平面上会出现“反麦卡托”效果：会使边缘看起来非常小。埃舍尔（Esher）那幅著名的《圆的极限Ⅳ》，就是一幅带有负曲率的弯曲空间的地图^[213]，精确地展示了二维AdS片层的样子。

我发现《圆的极限Ⅳ》具有催眠作用。（这使我想起了《老鼠和他的孩子》以及其中主人公对最后一只可见狗的永久找寻，见第20章。）这些天使和魔鬼无休止地一再出现，直至消失在无限分形的边界中。是埃舍尔跟魔鬼做了一笔交易，让他能够画出天使无数？还是，只要我拼命看，就能看到最后一个可见天使？

稍停一会儿，重新整理一下你的大脑，将那些天使和魔鬼都想象成一样大小。这并不是一个简单的智力体操，但是它有助于你回想起格陵兰岛的面积与阿拉伯半岛几乎完全一样，尽管前者在麦卡托地图上看起来要比后者大8倍。显然，埃舍尔对这类思维练习特别在行，但是通过实践你也可以掌握它的要领。

现在让我们再花一些时间，总结一下在反德西特空间中的图像。跟以往一样，我们用竖轴表示时间。每一个横向片层代表一个在特定时刻的普通空间。这里将AdS看作是由无数个空间片层构成的——一根被切成无限多个薄片的意大利蒜味香肠——如果把这根香肠不断地往上堆叠就可以形成一个时空连续统。

AdS中的空间以一种离奇的方式弯曲着，但是并没有时间那么怪异。回忆前面第3章，在广义相对论中，不同位置上的时钟走的速率是不同的。例如，一只靠近黑洞视界的钟会越走越慢，这也使得黑洞可以被看成是一个时间机器。在AdS中，时钟也表现得很怪异。设想每一个魔鬼都戴着它们自己的手表。最接近中心的魔鬼们，环视一下四周那些相对离中心远一些的邻居们，会发现一些奇怪的事情：距离较远的地方上的时钟，走的速率是他们自己的表的2倍。假设这些魔鬼都有新陈代谢，离得比较远的邻居的新陈代谢也会更快。事实上，每一次时间测量的结果，看起来似乎意味着加速，而且当测量一些更远的地方，时钟似乎走得还要快。每一个连续的环层都会比里面的那个走得快，直到靠近边界上的时钟走得太快，以至于中心附近的魔鬼看到的是一团正在旋转的模糊。

AdS时空的曲率产生了一个引力场，将所有东西都推向中心，即使在那里并没有什么东西。这个诡异的引力场的一个表现是，如果一个有质量的物体被移向边界的话，它将会被推回来，就跟弹簧上发生的基本一样。如果不外加任何作用，这个物体将会无休止地来回振动。第二个效应实际上就是硬币的另一面。一个向着中心的拉力和一个背着边界的推力是等价的。这个推力是一种不可抗拒的排斥力，使包括黑洞在内的所有东西都与边界没有任何联系。

造出来的盒子是用来放东西进去的，所以我们在盒子中放入几个基本粒子。不论我们把它们放在哪里，它们将会被拽向中心。单个粒子最终将绕着中心振荡，但是如果有两个或两个以上的粒子，它们可能会碰撞。引力——不是那个AdS中诡异的引力，只是普通的粒子间的引力吸引作用——可能会使它们聚成一团。加入更多的粒子会增加中心的压力和温度，这个聚团可能会被点燃而形成一颗恒星。如果再加入更多的质量，那么将会导致一个灾难性的坍缩：一个黑洞将会形成——一个黑洞被捕获在一个盒子里面了。

巴纳多斯、泰特尔鲍姆和扎内利并不是第一个研究AdS中黑洞的人；这个荣誉应该给唐·佩吉和史蒂芬·霍金。但是BTZ发现了最简单的例子，这个例子很容易想象，因为其空间只有二维。这里有一幅关于BTZ黑洞的图像。黑色的区域的边界是视界。

除了一个例外，反德西特黑洞具有所有普通黑洞应该有的特点。如往常一样，视界里面藏着一个让人非常讨厌的奇点。增加质量会导致黑洞尺寸的增加，并把视界推向边界。

但是与普通黑洞不同，AdS黑洞并不会蒸发。视界是一个无穷尽的热源，不断地辐射光子。但是这些光子没有地方可去。它们又会再一次掉入黑洞，而不是蒸发到外部的空间中。

再说一点反德西特

设想放大《圆的极限Ⅳ》边界上的点，使它膨胀，以至于边界看上去完全是平直的。

我们可以一次次重复上述做法，直到最后边界看上去是笔直而且无限的，这并不需要我们对每一层的天使和魔鬼都进行放大处理。我不是埃舍尔，我没法复制他这幅优美的作品，但是如果为了简化起见，我们用方块取代魔鬼，这幅图就会变成某种格状图案，越接近这种格状图案的边界，其方块就越小。我们可以把AdS看成是一堵有无限多砖块的墙。当你每下一层，砖块都会变大一倍。

当然，在反德西特空间中并没有真实的线，就像地球表面上没有经线和纬线一样。它们只是用来告诉你的眼睛，尺度是怎么因空间的曲率而变形的。

埃舍尔的画和我这个粗糙的版本表示的都是二维空间，但是真实的空间是三维的。想象空间添加一维后的样子并不困难。我们要做的就是把用三维的立方体取代方块。在下面的图中，我将给出一堵三维的“砖墙”，不过在你脑中要想象这堵墙在水平方向和垂直方向都是无限延伸的。

与以往一样，给这幅图加入时间维：给每一个方块或者立方体配上自己的时钟。时钟运行的速率，取决于他们在哪个层面上。我们每接近边界一层，时钟都会被加速一倍。相反的，如果我们沿着墙往下走，那么时钟将会变慢。

从数学的角度来看，没有理由把空间停在三维。通过堆砌各种大小不一的四维的立方体，我们可以构建4+1维反德西特空间，或者任意其他维数的空间。但是画一个四维的立方体是极其复杂的。这里我们尝试一下。

这种把它们堆在一起形成四维版本AdS的尝试，会导致令人沮丧的混乱。

盒中乾坤

保持黑洞不辐射是研究盒子中物理的好理由，但是盒中世界的这个想法远不止于此。真正的目的是要了解全息原理并使它在数学上变得精确。这里就是我在第18章中解释全息原理所说的：“平常经验下的三维——充满了星系、恒星、行星、房子、巨石和人的宇宙——是一幅全息图，一幅在遥远的二维面上编码的关于现实的图像。这个新的物理学规律被称为全息原理，它认为一个空间区域中的所有东西都可以用边界上的信息来描述。

全息原理的不精确性，部分原因在于有东西是可以穿越边界的；毕竟这只是一个数学上假象的表面，没有任何真实的东西，所以物体是可以进出该区域的。这使得“空间区域内的每一样东西都可以用边界上的信息所描述”，这个论述变得让人困惑。但是在一个墙壁难以渗透的盒子中的一个世界将不会有这个问题。新的表述是：

一个外壳难以渗透的盒子中，所有东西都可以用储存在墙上的像素的信息来描述。

1989年在智利的旅行巴士上，我不明白克劳迪奥·泰特尔鲍姆，为什么要对反德西特空间那么兴奋。一个盒子中的黑洞——那又怎么样？我花了8年才了解到这一点，这一次是通过另一个南美洲的物理学家，一个阿根廷人。

马尔达西纳的惊人发现

胡安·马尔达西纳与克劳迪奥·泰特尔鲍姆在各方面都不同。他不高而且冷静许多。我很难想象他穿着一套假军服，迅速地穿越危险的圣地亚哥的样子。而作为一个物理学家，他并不缺少勇气。在1997年他冒险提出了一个极其大胆的想法，一个与我在泰特尔鲍姆车上听到的一样疯狂的想法。事实上，马尔达西纳认为，两个看起来并不相似的数学世界实际上是相同的。一个（4+1）世界有四维的空间和一维的时间，而另一个是更像我们所生活的世界的（3+1）维。我将简化一下这个故事，对每一种情况都降低一维，使它变得更容易想象一些。根据这样的简化，我可以说平地的某种虚构的版本，或多或少都会与一个（3+1）维的反德西特世界相等价。

这怎么可能呢？关于空间最明显的特征就是维数。无法确定空间维数，是一个极其危险的感知混乱。把二维错误地看成三维显然是不可能的，至少在理智和冷静的时候，或者你会那么想。

马尔达西纳的发现其过程是一条崎岖而曲折的路。他在极端黑洞，D-胚和一些叫作矩阵理论的东西之间徘徊^[214]，并最终以一个对全息原理非同寻常的证明结束。

整套论证是从波尔钦斯基的D-胚开始。我们还记得一个D-胚是一个实物物体，可以是空间的一个点，一条线，一个面或者是一块充填空间的三维物体，这取决于其维度。D-胚区别于其他东西的特性就是基本弦可以在其上面终结。更具体点，我们考虑D2-胚^[215]。考虑一个在三维空间中飘浮的平坦的二维平面，就像一块飞毯。开弦把它们的两头都连在D-胚上面。它们可以在D-胚上面滑动，但是它们不能跳入第三维。弦上的这些部分，就好比在一块没有摩擦的冰上滑冰的人，但是不能抬起他们的脚。从远处看起来，弦上的每一个部分就好像一个在二维世界中移动的粒子。如果有更多的弦，它们可能会碰撞，并结合形成更加复杂的东西。

D-胚可以独自存在，但是它们黏性很强。如果把它们轻轻地带到一块，它们将黏在一起并形成一个有若干层的复合胚，就像下图所示的一样。

我已经证明了D-胚是各自分立的，但是当它们结合在一起的时候，缝隙就消失了。一组结合在一起的D-胚被称为是D-胚垛。

开弦在一个D-胚垛上面的移动，比在单个D-胚上的运动有着更丰富和多变的特性。弦的两端可以黏在垛中不同的胚上，就仿佛一块滑板在略有不同的两个平面上滑行。要追踪这些不同的胚，我们可以给它们定个名字。例如，在上面显示的垛中，我们可以分别称它们为红色、绿色和蓝色。

在D-胚垛上滑动的弦其端点必定连在一个D-胚上，但是现在出现了若干种可能性。例如，一根弦的两端可以都连在红色胚上。那么这根弦为红—红弦。类似的还有蓝—蓝弦和绿—绿弦。但是弦的两端也可以被连在不同的胚上面。因此，还有红—绿弦、红—蓝弦，等等。实际上，在D-胚垛上移动的弦有9种不同的可能性。

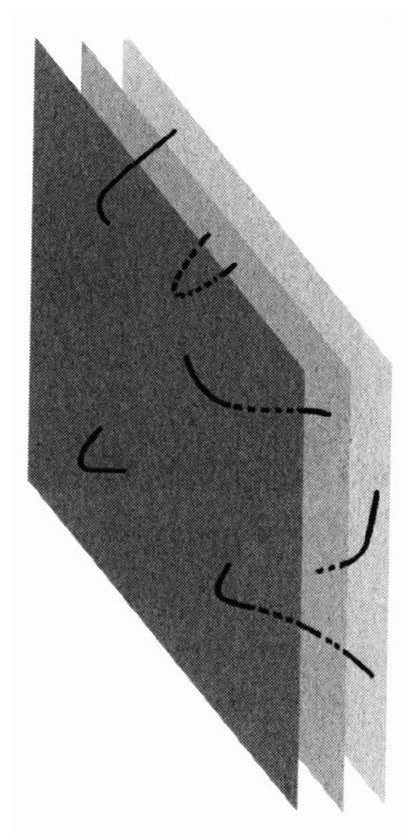
如果若干条弦被连在这些胚上，会有一些有意思的事情发生。

在D2-胚垛上的弦看起来跟普通的粒子很相似，虽然是在一个只有二维的世界中。它们之间相互作用，当它们相撞时会散射，它们也会给相邻的弦施加作用力。一根弦还可以分裂成为两根弦。这里有一组图，描述了一根单个胚上的弦是如何分裂成为两根弦的。时间的顺序是从上到下发展的。

一开始弦上的点与胚以某种方式相关联。在这种方式中所有的端点必须都是连在胚上面的，但是允许弦分裂成两根。而这幅图从下往上来看，就是一对弦结合形成一根单独的弦。

这组图画的是在3D-胚垛上的弦。这组图描述了一根红—绿弦与一根绿—蓝弦相撞。这两根弦结合并形成了一根单根的红—蓝弦。

一根红—红弦不能与一根绿—绿弦相结合，因为它们的端点永远不存在相接处。

你是不是感觉你曾经见过这些？如果你读过第19章，你就见过。支配着连接在D-胚垛上的弦的规则与量子色动力学中胶子的规则完全一样。在第19章中，我曾说过一个胶子就像一根带有两极的磁棒，每一端被标上一种颜色。相似的还不只是这些。上面的图，很像QCD中胶子的顶角图。

“D-胚上的物理”和通常世界的粒子物理的相似性令人兴奋和着迷，而且还极其有用。在下一个章节中我们将会看到这些。物理学家们将描述同一个系统的两种不同的方式称为“是相互对偶的”。光是波或粒子的对偶描述就是一个例子。物理学中到处都是对偶关系，所以对于马尔达西纳发现两种D-胚上面弦的对偶描述，并没有什么特别值得惊奇的。什么是新的呢，是闻所未闻的呢^[216]？就是这两种描绘的世界带有不同空间维。

我已经暗示了其中一种描述为（2+1）维平地版本的QCD。它描述了平坦空间的质子、介子和胶子球，但是不像真实的QCD，这里不包含有引力。与之对偶的另一半，即，描述同样的东西的另一种方式，描绘了一个三维空间的世界，但并不是任意的三维空间，而只是反德西特空间。马尔达西纳认为平地中的QCD与（3+1）维反德西特宇宙是对偶的。而且，在这个三维世界中，物质和能量行使的引力，就像在真实世界中一样。换句话说，一个（2+1）维包括了QCD而不含引力的世界等效于一个（3+1）维的带有引力的宇宙。

这是为什么呢？为什么一个只有二维的世界，会与三维的那个完全一样呢？那个额外的空间维是从哪里来的呢？关键在于反德西特空间的形变使得边界附近的物体看起来比在空间内部的物体要小。形变不仅会影响这些想象中的魔鬼，而且也会影响穿过空间的真实物体。例如，如果一个人把一个1米大小的字母A投影在边界上，那么这个图像会随着物体靠近或远离边界而缩小或放大。

从三维空间内部的角度来看，这只不过是一个幻象，就像在麦卡托地图上巨大的格陵兰岛。但是在对偶描述中——平地理论——在这个正交的第三维上面并没有距离这个概念。取而代之的则是一个尺寸的概念。这是一个非常令人意外的数学联系：在对偶的平地这一半中放大或缩小，与在对偶的另一半中的第三个方向上来回移动完全一样。

这应该看起来很眼熟，这一次是来自第18章，我们发现这个世界是某种全息图像。马尔达西纳的两种对偶的描述是全息原理的应用。每一样发生在反德西特空间内部的事情，“是一幅全息图，一张关于在遥远的二维面上的关于现实的图像”。一个三维的带有引力的世界等价于一幅空间边界上的二维的量子全息图。

我不知道马尔达西纳是否把他的发现和全息原理联系起来了，但是威顿不久就那么干了。就在马尔达西纳发表论文的2个月之后，威顿在互联网上发表了他的论文，题目就是“反德西特空间和全息原理”。

威顿论文中特别吸引我的就是关于黑洞那个章节。反德西特空间——原初的版本，而不是那个平坦的砖墙那个版本——就像一罐头汤。水平穿过罐头的片层代表了空间，罐头的竖轴代表时间。罐头外面的包装纸是边界，而内部则是时空连续统。

纯AdS就像一个空的罐头，但是如果将里面填入“汤”——物质和能量，会变得更加有趣。威顿解释道，如果往罐头里面注入足够多的物质和能量，一个黑洞就会产生。这就会出现一个问题。根据马尔达西纳的观点，那里必定有第二种描述——一种对偶的描述——在那里不需要参考罐头内部的东西。这种描述用的是粒子的二维的量子场论语言，类似于胶子在包装纸上的移动。汤里面存在着一个黑洞，一定等价于边界上的全息图上的某些东西，但是到底是什么东西呢？在边界理论中，威顿认为汤中的黑洞，等价于一种普通的基本粒子的热流，这种粒子基本上可认作是胶子。

当我看到威顿文章的时候，我知道黑洞的战争已经结束了。量子场论是量子力学的一种特殊的情况，量子力学中的信息永远不会被毁灭。不论马尔达西纳和威顿还干了什么，他们确切地证明了信息永远不会被丢失在一个黑洞的视界后面。弦论学家们会马上意识到这一点，而相对论学家们要花长一点的时间。但是战争已经结束了。

虽然这场黑洞的战争应该在1998年早些时候结束的，但是史蒂芬·霍金就像一个在丛林中游击多年，却不知道战争已经结束的不走运的士兵。这个时候，他成了一个悲剧式的人物。56岁，智力不再处于巅峰，与外界几乎不能再交流，霍金并不知道到底发生了什么。我很确定，这并不是因为他的智力局限。从我跟他在1998年之后的一些接触中，很明显发现他的脑子依旧极其敏捷。但是他的生理能力恶化得非常严重，他几乎完全被锁进了自己的脑袋。不能写一个方程，与他人合作也非常困难，他一定知道，他无法去做物理学家们为了解不熟悉的新理论，通常要做的事情。所以霍金继续战斗了一段时间。

在威顿发表了他的论文不久之后，另一个会议在圣芭芭拉召开，这一次是为了庆祝全息原理和马尔达西纳的发现。宴会之后的派对的发言人是杰夫·哈维（CGHS中的H），他带领大家和着《玛卡莲娜》的旋律^[217]，唱起了《马尔达西纳》之歌，跳起了胜利之舞。

取胚伊始

乃B P S^[218]。

操之近之，

是A D S。

胚之何谓，

非我所知。

呃！马尔达西纳！

杨米尔斯，

超对称场。

幺正规范，

大哉之数。

球面引力，

流之未央。

君言相同，

乃有全息。

黑洞之谜，

D胚D熵。

D胚有热，

热是能量。

呃！马尔达西纳！

胡安告成，

斗志昂扬。

洞察黑洞，

战绩彰彰。

色动力学，

尽可估量。

胶子球谱，

尚待议商。

呃！马尔达西纳！

第23章　核物理？开玩笑吗

持怀疑态度的人会指出我所告诉你的都只是纯粹的理论，关于黑洞的量子特性的所有事情，从熵、温度和霍金辐射一直到黑洞互补性原理以及全息原理，都没有实验数据可以证实。不幸的是，在今后很长的时间内，他们所说的可能都是正确的。

也就是说，一个完全没有预料到的联系，最近被建立起来了，一个连接黑洞、量子引力、全息原理和实验核物理，这些一直被认为无法被科学验证的理论之间的联系被建立起来了。从表面上来看，要来检验类似全息原理和黑洞互补性原理这样的理论，核物理似乎是一个最没希望的平台。一般认为核物理并不属于前沿。它是一个古老的领域，而且包括我在内的大多数物理学家，认为它已经被发掘殆尽，无法再教给我们任何关于基本原理的新东西。从现代物理学的观点来看，原子核就像一个柔软的果浆软糖——硕大的扁球里面大部分地方是空的^[219]。它们能告诉我们普朗克尺度下的物理是怎样的呢？出人意料的是，它们似乎能告诉我们很多东西。

弦论学家一直对原子核很感兴趣。在弦论之前的历史几乎都是关于强子的：质子、中子、介子和胶子球。就像原子核一样，这些由夸克和胶子构成的粒子很大。但是就在这比普朗克尺度大几百亿亿倍的尺度上，自然复制了它自己。关于强子物理学的数学，与弦论的数学几乎一样。如果考虑到它们的尺度是那么不同：核子要比基本弦大10²⁰倍，振荡也要慢10²⁰倍，这一切简直不可思议。这些理论为什么会是相同的，难道会完全不相关？然而，有一个办法可以使这些都明晰起来。如果普通的亚原子核尺度下的粒子确实与基本弦类似，那么为什么不在核物理实验室中去测试弦论的那些想法呢？实际上，这已经做了近40年了。

强子和弦之间的联系，是现代粒子物理学的支柱之一，但是直到最近，仍然无法检验黑洞物理学的原子核类比。但是这种状况正在发生改变。

在长岛，大约离曼哈顿70英里，布鲁克海文国家实验室的核物理学家们正在用重原子核做撞击实验。相对论性重离子对撞机（RHIC）把金的原子核加速到接近光速——只要在它们碰撞的时候速度足够快，便可以制造出大量的能量，温度高达太阳表面温度的10亿倍。布鲁克海文的物理学家们对核武器或其他核技术并不太感兴趣。他们的动机纯粹出于好奇心——对于新的物质形式的特性的好奇。这些热的核物质的行为是怎样的？它们是气体？液体？它们会结合在一起，还是立刻蒸发变成分离的粒子？极高能粒子的粒子流会从中逃逸出来吗？

如我所说的，核物理和量子引力是发生在完全不同的尺度上面的，它们怎么可能相互有联系呢？我所知道的最好的类比涉及一部史上最烂的电影，一部露天电影时代的老的恐怖片。电影的主角是一只巨型的苍蝇。我不知道这部电影是怎么拍摄的，我想是拍了一只普通的家蝇，然后放大到撑满整个屏幕。这幅图像用非常慢的速度投影，这使得这只苍蝇看起来像一只巨大而可怕的鸟。效果是恐怖的，但是更重要的是，它很好地示意了引力子和胶子球之间的关系。都是闭弦，但是引力子要比胶子球小得多，运动速度也快得多。强子似乎很像基本弦变大和减慢后的图像，但是这里不是像苍蝇一样的几百倍，而是令人难以置信的10²⁰倍。

所以，如果我们不能用极高能量的普朗克尺度粒子的碰撞来制造出黑洞，也许我们可以用它们放大后的版本——胶子球、介子或核子做碰撞——产生一个放大版的黑洞。但是等一下，这样就不需要大量的能量了吗？是的，它不需要，为了理解原因，我们需要回忆一下在第16章中20世纪的大小和质量间反直觉的关系：小的是重的，大的是轻的。核物理发生的尺度要比基本弦理论的尺度大很多，这意味着，集中在一个大得多的体积内，相应现象所需要的能量要少很多。当我们代入数字并进行计算后，在RHIC的普通的核碰撞中，一些非常类似于慢速的放大的黑洞的东西应该形成。

为了了解RHIC是如何制造黑洞的，我们必须回到全息原理和胡安·马尔达西纳的发现。马尔达西纳以一种前人没有预见过的方式，发现两种不同的数学理论实质上是相同的——用弦论的行话讲就是“互相对偶”。存在一种带有引力子和黑洞的弦理论，不过是在（4+1）维的反德西特空间（AdS）中。（在第22章中，为了方便想象，我降低了维数。在这章中，我恢复那个去掉的维度。）

四维空间对于核物理来说，它太大也太烦了，但是记住全息原理：发生在AdS空间中的所有事情都可以用少一维的空间的数学理论完备描述的。因为马尔达西纳是从四维空间开始的，所以全息的对偶理论只有三维，这是我们每天生活的空间的维数。这个全息描述，真是类似于任何一个我们用来描述传统物理学的理论吗？

这个答案是肯定的：全息对偶在数学上与关于夸克、胶子、强子和原子核的量子色动力学（QCD）非常相似。

AdS中的量子引力↔QCD

对我来说，主要兴趣在于马尔达西纳是如何证明全息原理，以及如何把量子引力的工作方式表述清楚的。但是马尔达西纳和威顿看到了另一次机会。他们意识到全息原理是一条双通道的路，我必须说这是一个非常聪明的看法。为什么我们不反过来去看呢？即用我们所知道的引力的知识——在这种情况下，是AdS中（4+1）维的引力——告诉我们关于普通量子场论的东西呢。对我而言，这可是一个完全没有想到的脑筋急转弯，一个全息原理带来的额外的从未想过的奖赏。

要完成这些，还需要一点点工作。QCD与马尔达西纳的理论并不是完全相同，但是主要的差异可以通过对AdS的一种简单修正来消除。回顾AdS，让我们从一个非常接近边界的位置来看（最后一个可见的魔鬼的地方）。我把那个边界叫做UV-胚^[220]。UV的意思为紫外，这个术语也用来形容短波长的光。（这些年来紫外这个词，开始代表那些在小尺度上的任何现象。在这里，这个词讲的是埃舍尔画中边界附近渐渐缩小成无穷小的天使和魔鬼。）UV-胚这个词中，胚这个字确实是用词不当，但是因为它已经那么叫了，所以我也就用它了。UV-胚是一个接近于边界的面。

想象一下离开UV-胚进入内部，在那里魔鬼以平方的速率无限地变大，时钟也以平方的速率无限地变慢。当我们走向AdS深处的时侯，UV-胚附近那些既小又快的物体，变得又大又慢。但是AdS并不是描写QCD的正确的理论。虽然区别并不是很大，但是修正的空间需要它自己的名字；我们称其为Q-空间。就像AdS一样，Q-空间也有一个UV-胚，那里物体变小变快了，但是不像AdS，它有第二边界，被称为IR-胚（IR的意思是红外，一个用来描述长波长光的词）。这个IR-胚是第二个边界——一块难以渗透的屏栏，在那里天使和魔鬼达到最大。如果UV-胚是一块带有无限深裂缝的天花板，那么Q-空间是一个普通的有天花板有地面的房间。如果忽略时间维度，仅仅画二维的空间维度，那么AdS和Q-空间看起来就是：

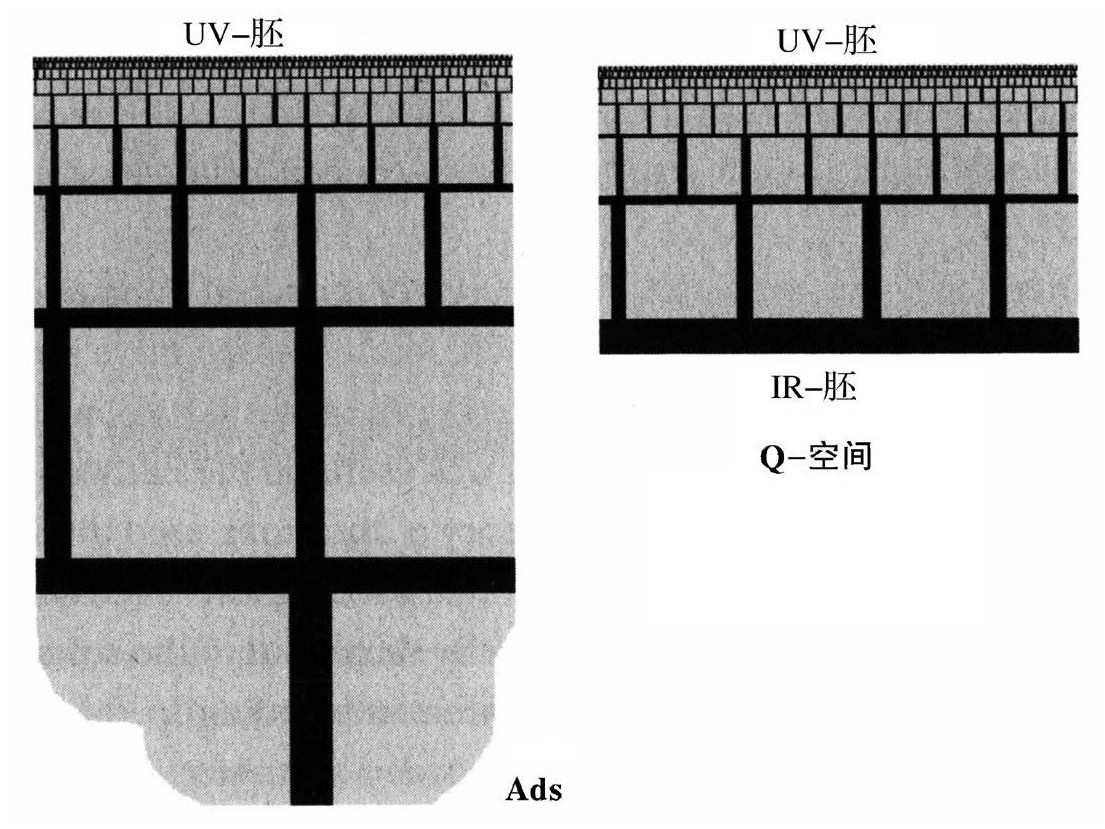
设想把一根弦状的粒子放入Q-空间，一开始放在UV-胚的附近。就好像有许多天使和魔鬼围绕着它，它将看起来十分的小——很可能是普朗克尺度的——而且极快速的振动。但是，如果同样的粒子移向IR-胚，它似乎会变大一些，就像被投影到一个后退的屏幕上。现在观察弦的振动。振动可以定义某种时钟，而且就像所有的钟一样，当它接近UV-胚的时候它高速振荡，当它移向IR-胚的时候速度就渐渐慢下来。一根IR边界附近的弦，不仅看起来是一根收缩的UV弦被放大的巨型版本，而且它会慢很多。这个区别听起来像真实的苍蝇，与它们的电影图像的区别一样——或者是基本弦和它们的核对应物的区别一样。

如果弦论中极其微小的普朗克尺度粒子“生活”在UV-胚附近而它们的放大版本——强子——生活在IR-胚附近，那么它们之间相隔多远呢？从某种意义上来说，并不是那么远；你只需要往下穿过大约66个魔鬼方块就能从普朗克尺度的物体到达强子。但是，记住每一步都是要比前面的大2倍。倍增66次等于膨胀了10²⁰倍。

对于基本弦和核物理之间的相似性有两种观点。一种相对保守的观点是认为它们是偶然的，或多或少就像原子和太阳系一样。这种相似性在原子物理的早期是有用的。尼尔斯·玻尔，在他的原子理论中用了牛顿用在太阳系的同样的数学。但是玻尔和其他任何人，都没有真正认为太阳系就是原子的放大版本。根据这种相对保守的观点，量子引力和核物理之间的联系只是一个数学上的类比，但是这个重要的类比，使得我们可以应用引力的数学，来解释某些核物理的特性。

让人更为兴奋的观点是，核弦跟基本弦实际上是同一样东西，只不过是通过透镜的扭曲使得它们的图像延伸速度减慢。根据这种观点，当一个粒子（或者弦）被放置在UV-胚附近时，它看起来很小，能量很高而且运动很快；所以它必定是一根基本弦。例如，一根在UV-胚上的闭弦会是一个引力子。但是同样的弦，如果它移动到了IR-胚附近，尺寸变大，速度变慢。从任何方面看，它看起来表现得都像一个胶子球。在这种观点中，引力子和胶子球是完全相同的东西，只是它们在胚上的位置不同。

设想一对引力子（在UV-胚附近的弦）要相互碰撞。

如果它们有足够的能量，当它们在UV-胚附近相撞时，一个普通的小型黑洞会形成：一个团能量会留在UV-胚上。这可以想象成一滴流体悬挂在天花板上面。组成它的视界的信息是普朗克尺度的。

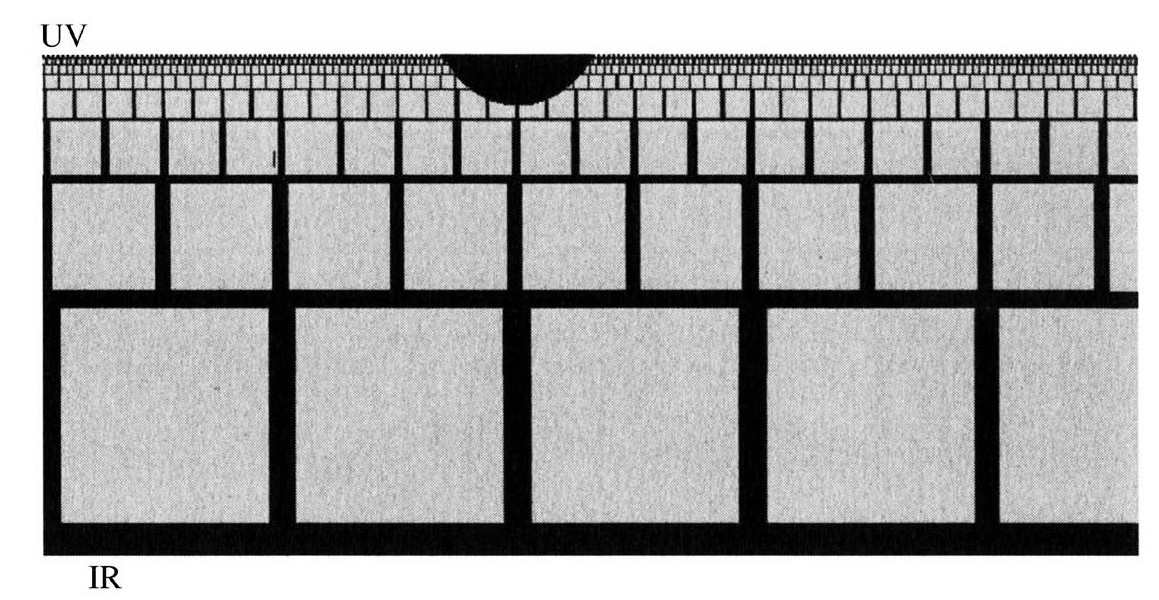
这当然是一个我们可能永远无法做的实验。

但是现在把引力子换成是两个原子核（在IR-胚附近的）并使它们相互撞击。

IR-胚附近即将相撞的两个原子核

这时对偶性显示其威力。一方面，我们可以用四维版本来看，在那里两个物体碰撞并形成一个黑洞。这时黑洞在IR-胚附近，就像地板上的一个巨大的水坑。这需要多少能量呢？要比在UV-胚附近形成黑洞少得多。实际上，对于RHIC来说这个能量很容易达到。

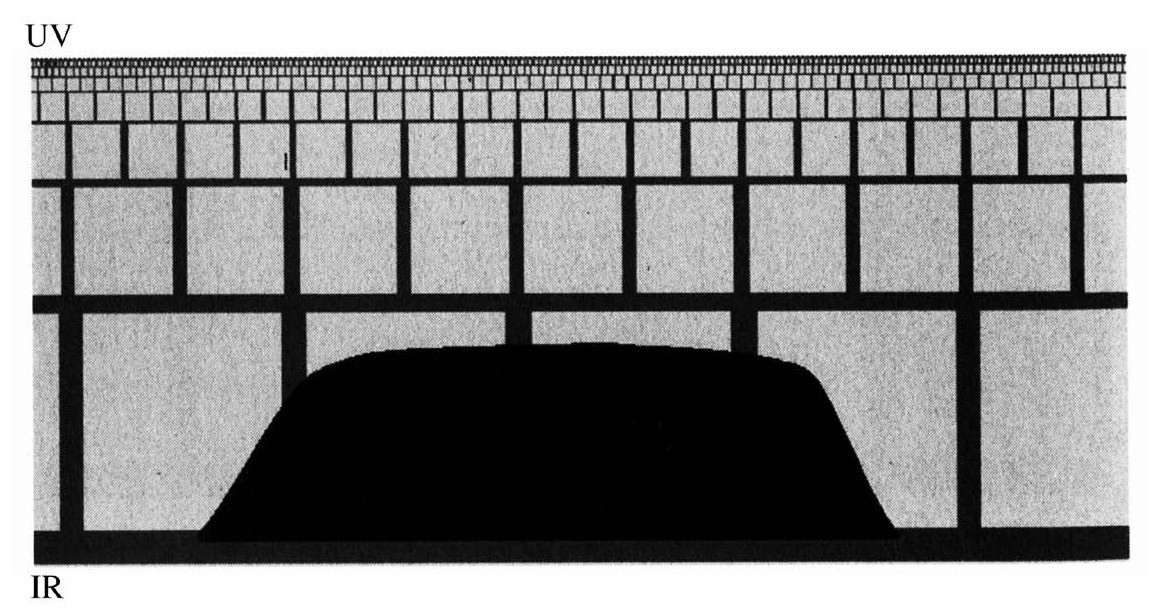
另一方面，我们还可以从三维的角度来看这个问题。在这种情况下，强子或原子核碰撞，并产出一堆夸克和胶子。

起初时，在任何人都没有意识到QCD可能会与黑洞物理有关系的时候，QCD的专家们已经预计到碰撞所产生的能量，会以一团粒子气的形式再次出现，这团气体不遇到任何阻力，并快速地散开。但是他们所看到的则完全不同：能量凝结成团，看起来很像一团流体——称为热夸克汤。热夸克汤并不真是什么流体，它有一些令人惊讶的流动特性，与黑洞的视界极为相似。

所有的流体都具有黏滞性。黏滞性是一种作用在流体中，有相对滑动的各个层面之间典型的摩擦力。黏度是一个物理量，用来区别黏滞性很强的流体，如蜂蜜，与不太黏的流体，如水。黏度并不只是一个定性的概念。而对于每一种流体来说，有一个精确的数值测量被称为剪切黏度^[221]。

理论学家们一开始就用了一些标准的近似方法，并得出结论：热夸克汤具有很高的黏度。而最终结果却是它的黏度小得令人惊讶^[222]。除了一些了解弦论的核物理学家，每个人对此都感到很意外。

根据对黏度的某种定量测量，热夸克汤是科学领域所知道的黏度最小的流体——要比水的黏度小很多。即使是超流体液氦（小黏度的前冠军）也要比它黏得多。

自然界中有什么东西，可以与热夸克汤的这种低黏度相匹敌呢？有，但是并不是一种通常流体。一个黑洞的视界在它被扰动时表现得也像一个流体。例如，一个小的黑洞掉进了一个大黑洞里面，大黑洞的视界上会产生一个临时的突起，类似于一滴蜂蜜，滴在一壶蜂蜜上面所产生的突起。这个视界上的突起就像在一个黏性流体一样传播。很久以前，黑洞物理学家们计算了视界的黏度，当转换成流体的语言时，它很轻松的击败了超流体氦。当弦论学家开始猜测黑洞和核碰撞之间的联系的时候^[223]，他们意识到所有东西中热夸克汤，是最类似于黑洞视界的东西。

什么东西最终会成为这团流体呢？就像一个黑洞，热夸克汤也蒸发，变成了各种类型的粒子，包括核子、介子、光子、电子和中微子。黏度和蒸发仅是视界和热夸克汤共同特性中的两种。

在研究核流体的热潮中，人们希望能够知道有没有其他特性能够显示与黑洞物理是相类似的。如果这个潮流继续下去，将意味着我们拥有了一个非凡的机会来证明霍金和贝肯斯坦的理论，以及黑洞互补性原理和全息原理。这是一扇探究量子引力世界的至关重要的窗口，在那里尺寸被放大了，频率被减缓了，这样普朗克距离不再比质子小很多。

有人说和平只是战争之间的短暂间隙。但是在科学上却跟战争相反，托马斯·库恩说得很对：大部分“普通科学”发生在巨变之间，是一个长期的、平静的、单调的过程。黑洞战争导致了物理学定律的一次疯狂的重建，但是现在我们看到它已经在那些天天都要用到的更普通的物理学中起到作用。就像先前许多次的革命性的想法一样，全息原理正在从激进的范式，渐渐地转变成核物理学每天都要用到的工具。

第24章　大成若缺

我们只是一些生活在一颗普通恒星的行星上的高级的猴子。但是我们可以理解宇宙。这使我们变得与众不同。

——史蒂芬·霍金

为了理解相对论，我们重新装备自己，这已经够难了。而如果是为了量子力学那更困难了。可预见性或者决定论必须离开，而失败的经典逻辑必须要被量子逻辑所取代。人们用抽象的无限维希尔伯特空间、数学上的对易关系以及其他一些怪异的发明来描述。

在整个20世纪的重新装备的过程中，至少到90年代中期，时空的实在性、事件的客观性已经是无可争议了。人们普遍认为量子引力在研究时空的大尺度特性时没什么用。史蒂芬·霍金以及他的信息佯谬，却无意或说是很不情愿地带我们走出了这个框架。

关于物质世界的新的观点在过去十多年的时间中不断地演变着，包括一种新的相对性原理和一种新的量子互补性原理。在1905年的时候，关于两个事件同时性的客观性就被否认了，但是事件本身这个概念却被坚实地保留了下来。如果一个核反应发生在太阳上，所有的观测者都会同意它发生在太阳上。没有人能在地球上观测到它。但是在引力作用极其强大的黑洞里，却出现了一些异常，一些破坏事件客观性的东西发生了。一件在自由下落的观测者看来是发生在巨型黑洞的内部的事件，在视界外部的另一个观测者看来却是在霍金辐射的光子中被“持球跑进”了。一个事件不能同时发生在视界内部和视界外面。同样的事件要么发生在视界后面要么在视界前面，这取决于观测者做的是哪个实验。但是互补性原理所有诡异的特性，在全息原理面前就成了小巫见大巫。立体的三维的世界似乎只是某种幻象，而真正的事情发生在空间的边界上面。

对于我们大部分人来说，一些像同时性（狭义相对论中的）和决定性（量子力学中的）这样的概念的崩溃，只不过是个别物理学家所感兴趣的晦涩而奇怪的事情。但是真实的世界截然相反：人类动作不自然的缓慢以及人身体内的10²⁸个原子都是自然界的特例。对于每个人而言，宇宙中存在着10⁸⁰个基本粒子。它们中大部分都以接近光速的速度运动，而且不是无法确定其位置就是无法确定其速度。

我们在地球上所感受到的引力作用之弱也是一个意外。宇宙在一个急速膨胀的状态中诞生；空间中的每一点都被一个半径比单个质子还小的视界所包围。宇宙中最著名的居民——星系——围绕着不断地吞噬着恒星和行星的巨型黑洞而形成。宇宙中每10 000 000 000比特信息中有9 999 999 999比特是与黑洞的世界相关的。显然，我们关于空间、时间和信息的这些幼稚的想法，用来了解自然是完全不够的。

量子引力的再装备过程，还远远没有完成。我不认为，我们已经有了一个能代替客观时空的老范式的合理框架结构。弦论强有力的数学是有帮助的，它使我们可以给出一个严格的框架，来验证那些我们只能在哲学层面争论的问题。但是弦论是一项未完成的，仍在继续中的工作。我们不知道它的确定原理，也不知道它是现实世界的最基本的描述，还是征途中另一个暂时性的理论。黑洞战争告诉我们一些非常重要而又出人意料的东西，但是它们仅仅是一个暗示，用来告诉我们现实与我们脑中的图像是如此的不同。即便是在我们用相对论和量子力学重新装备过之后，情况仍然如此。

宇宙视界

黑洞战争已经结束（这样讲可能会使很多还在为此战斗的人感到沮丧），但是就算它结束了，自然界，这个伟大的好事者，又投给了我们另一个曲线球^[224]。在马尔达西纳发现的同时，物理学家开始确信我们生活在一个有着非零宇宙学常数的宇宙中。一个小得出奇的自然常数^[225]，比任何物理学常数都要小，宇宙学常数是宇宙未来的主宰者。

宇宙学常数，也被称为暗能量。近一个世纪以来，它一直是物理学家们感到烦恼的事情。1917年，爱因斯坦推测有一种反引力，它可以使宇宙中每样物体都排斥其他物体，以此来抵消通常引力的吸引作用。这个猜想并不是没有根据的，它是严格基于广义相对论的数学的。该方程有一个额外项的自由度，这个额外的项被称为宇宙学项。这种新作用的强度与一个新的自然常数成正比，即所谓的宇宙学常数，这个常数用大写的希腊字母Λ表示。如果Λ是正的，那么宇宙学项便会产生随距离增加而增加的排斥力；如果是负的，那么这个新的作用力则是一种吸引力；如果Λ是零，那么没有新的作用力，我们可以忽略它。

起初，爱因斯坦猜测Λ是正的，但是不久之后他开始讨厌整个想法，并称它是他一生中最大的错误。在他后半生中，他在他所有的方程中把Λ都设成零。虽然大部分物理学家不知道为什么Λ应该在这些方程中消失，但是他们都同意爱因斯坦。然而几十年过去了，人们又开始相信天文上存在一个正的小的宇宙学常数。

这个宇宙学常数，以及所有由它所产生的难题和佯谬，在我的《宇宙概况》中都有讲到。这里我只是告诉你最重要的结果：作用在宇宙学距离上的排斥力，会使空间指数式膨胀。宇宙在膨胀，这没什么新鲜的，但是没有宇宙学常数，这个膨胀速率是逐渐减小的。实际上，宇宙膨胀有可能会停止膨胀反而开始收缩，最终导致一个内向的大坍缩。与之相反，如果存在宇宙学常数的话，那么宇宙似乎每隔150亿年就会变大一倍，而且所有的迹象显示这种方式没有尽头。

在一个膨胀的宇宙中，或者对于一个膨胀的气球，两点间的距离越大，它们相对彼此后退得越快。这个距离和速度的关系被称为哈勃定律：两点间的退行速度与它们分开的距离成正比。对于任意观测者来说，不论他在哪里，环视四周便会发现那些遥远的星系都在远离他而去，它们的速度正比于它们与他之间的距离。

在这个膨胀的宇宙中，如果你可以看得足够远，那么你将会看到有一个点，那里的星系正在以光速远离你。一个指数式膨胀的宇宙，最显著的特征就是这个点的距离是不会改变的。在我们的宇宙中，约在150亿光年的地方的物体是以光速远离我们，更重要的是它们将永远以这种方式在退行。

这些东西听起来挺熟悉但又略有不同。它使我想起第2章中的蝌蚪湖。如果爱丽丝随着水流下去，她将穿过一去不复返点，并以声速远离鲍勃。类似的事情现在也同样发生在一个极大的尺度上面。我们从每一个方向观察，星系正在穿过那个点，在那个点上它们远离我们的速度将超过光速。我们每一个人都被一个宇宙学视界所包围——一个球面，其上所有的东西都以光速退行——因而没有信号可以从这个面之外的地方传达到我们这里。当一颗恒星穿越这个一去不复返点时，它将永远地消失了。现在看来，约在150亿光年的地方，我们的宇宙学视界正在吞噬着星系、恒星，还可能有生命。这就好像我们生活在我们自己的隐秘的里面朝外的黑洞中。

会不会存在着这样一些世界，它们很早以前就穿越了我们的视界，又与我们的世界类似，而且它们与我们所能观测的任何东西都完全无关？更糟的是，我们是不是永远无法了解宇宙中的大部分区域？这对于一些物理学家来说，是极其困扰人的。有一种哲学认为如果某些东西是不可观测的，从原则上是不可观测的，那么它将不属于科学范畴。如果没有办法证伪或证明一个假说，那么它与占星术和唯灵论一样都属于形而上学的猜想。以这种标准来看，宇宙中的大部分区域都没有真实的科学——只是我们通过想象来臆造的东西。

但是，将宇宙的大部分区域认为是没有价值的而摒弃又是难以接受的。并不存在任何证据，显示星系在视界上面慢慢变暗或者消失。天文观测表明在我们眼睛或望远镜所能看到的地方，它们还安好地存在着。我们该怎么理解这种情形呢？

以往在许多其他领域中有很多“不可观测”的东西被认为属于科学范畴而不予考虑。他人情感就是一个很著名的例子。整套行为主义^[226]心理学所基于的原理就是认为情感和内在的意识状态是不可知的，所以它不应该出现在科学讨论中。只有实验上可观测的行为——人的身体活动、面部表情、体温、血压——才是行为主义心理学研究的对象。行为主义在20世纪中期影响力很大，但是今天大多数人认为它只是一种极端的观点。也许我们应该像承认他人内在生活是不可知那样，承认视界之外的宇宙是不可知的。

然而，可能有一个更好的答案。宇宙视界的这些特性看起来与黑洞的特性很相似。一个加速宇宙（特别是指数式膨胀的）的数学暗示着当有东西靠近宇宙视界的时候，我们会看到它们变慢。如果我们可以送一支温度计到这个宇宙视界的附近，那么我们会发现温度不断地上升，直到在视界面上温度趋向了无穷大。难道这意味着所有生活在遥远的行星上的人们正在被烧烤？答案就是他们跟在一个黑洞附近一样。对于一个随着膨胀穿越宇宙视界的观测者来说，这只是一个数学上的一去不复返点，并没有什么大不了的。但是，根据我们的观测，再配合上一些数学上的分析，我们发现他们正在靠近一个温度高得难以置信的区域。

那么它们的信息会发生什么变化呢？霍金用于证明黑洞辐射黑体谱的论证，同样可以用来告诉我们宇宙视界也在辐射。但是在这里，这种辐射不是向外的而是向内的，就像我们生活的房间的墙壁正在做热辐射。以我们的观点来看，当东西向视界运动的时候，它们很可能会被加热，并以光子的形式辐射回来。有没有可能存在一个宇宙学互补性原理呢？

对于一个宇宙视界内部的观测者来说，视界是一个由视界原子所组成的炙热表层，这些视界原子吸收，“持球跑进”，而且还退回所有信息。对于一个穿越了宇宙视界的自由运动的观测者来说，这种穿越没什么异样的地方。

然而，现在我们对宇宙视界知道得非常少。关于视界后面的物体的意义——它们是否真实，它们在我们对宇宙的描述中占什么样的地位——可能会是宇宙学中最深刻的问题。

下落的石头和轨道中的行星，都不能很好地告诉我们引力究竟是什么？黑洞是引力研究的适当场所。黑洞不仅仅是一个致密的星体，更是一个终极的信息储存器，在那里信息被紧紧地包裹起来就像一个二维的炮弹堆，但是尺度要小34个数量级。这就是量子引力：信息和熵被紧紧地包裹起来。

霍金关于自己的问题所给的答案可能是错的，但是这个问题本身，是这些年来物理学上意义最为深远的一件事情。可能是他的经典图像过于根深蒂固——很容易认为，尽管时空可以变形，但也不过是一块物理学用来描绘世界的先验的画布——以至于不承认调和量子信息守恒和引力相互作用的深远意义。但是问题本身却打开了一条通向下一个物理学重大观念革命的道路。没有几个物理学家可以给出那个观点的。

霍金所带给我们的财富是非常巨大的。在他之前其他人也意识到了，引力和量子理论的不匹配会在某一天被消除，但是贝肯斯坦和霍金是第一个进入这个遥远国度，并带回来金子的人。我希望将来的科学史专家们会说，是他们开始了这一切。

一个从未尝试过失败的人是不会有伟大的成就的。

——赫尔曼·梅尔维尔（Herman Melville）^[227]

果壳中的物理学

人们迷惘、没有方向；因果破却，确定性丧失；所有一切旧的规律都失效。这就是一个占支配地位的范式崩溃之时所发生的事情。

但是，接着一个新的模式出现了。起初它们是荒谬的，只是模式而已。接着应该做什么呢？将这个模式分类、量化并且用新的数学编码，如果必要的话还要用新的逻辑。用新的装备取代旧的并且慢慢熟悉它。亲不敬，熟生蔑^[228]，或者至少是接受它。

我们很可能仍是一些满脑子错误图像的深感迷惑的初学者。终极的现实离我们还很远。这让人想到那个古老的绘图学里的术语，未发现的地域（terra incognita）。我们了解得越多，剩下的未知就越少。这就是果壳中的物理学。