NumPy的ndarray：一种多维数组对象

NumPy的ndarray：一种多维数组对象

NumPy最重要的一个特点就是其N维数组对象（即ndarray），该对象是一个快速而灵活的大数据集容器。你可以利用这种数组对整块数据执行一些数学运算，其语法跟标量元素之间的运算一样：

In [8]: data
Out[8]:
array([[ 0.9526, -0.246 , -0.8856],
       [ 0.5639,  0.2379,  0.9104]])
 
In [9]: data * 10                     In [10]: data + data
Out[9]:                               Out[10]:
array([[ 9.5256, -2.4601, -8.8565],   array([[ 1.9051, -0.492 , -1.7713],
       [ 5.6385,  2.3794,  9.104 ]])         [ 1.1277,  0.4759,  1.8208]])

ndarray是一个通用的同构数据多维容器，也就是说，其中的所有元素必须是相同类型的。每个数组都有一个shape（一个表示各维度大小的元组）和一个dtype（一个用于说明数组数据类型的对象）：

In [11]: data.shape
Out[11]: (2, 3)
In [12]: data.dtype
Out[12]: dtype('float64')

本章将会介绍NumPy数组的基本用法，这对于本书后面各章的理解基本够用。虽然大多数数据分析工作不需要深入理解NumPy，但是精通面向数组的编程和思维方式是成为Python科学计算牛人的一大关键步骤。

注意：当你在本书中看到“数组”、“NumPy数组”、"ndarray"时，基本上都指的是同一样东西，即ndarray对象。

创建ndarray

创建数组最简单的办法就是使用array函数。它接受一切序列型的对象（包括其他数组），然后产生一个新的含有传入数据的NumPy数组。以一个列表的转换为例：

In [13]: data1 = [6, 7.5, 8, 0, 1]
 
In [14]: arr1 = np.array(data1)
 
In [15]: arr1
Out[15]: array([ 6. ,  7.5,  8. ,  0. ,  1. ])

嵌套序列（比如由一组等长列表组成的列表）将会被转换为一个多维数组：

In [16]: data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
 
In [17]: arr2 = np.array(data2)
 
In [18]: arr2
Out[18]:
array([[1, 2, 3, 4],
       [5, 6, 7, 8]])
 
In [19]: arr2.ndim
Out[19]: 2
 
In [20]: arr2.shape
Out[20]: (2, 4)

除非显式说明（稍后将会详细介绍），np.array会尝试为新建的这个数组推断出一个较为合适的数据类型。数据类型保存在一个特殊的dtype对象中。比如说，在上面的两个例子中，我们有：

In [21]: arr1.dtype
Out[21]: dtype('float64')
 
In [22]: arr2.dtype
Out[22]: dtype('int64')

除np.array之外，还有一些函数也可以新建数组。比如，zeros和ones分别可以创建指定长度或形状的全0或全1数组。empty可以创建一个没有任何具体值的数组。要用这些方法创建多维数组，只需传入一个表示形状的元组即可：

In [23]: np.zeros(10)
Out[23]: array([ 0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.])
In [24]: np.zeros((3, 6))
Out[24]:
array([[ 0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.]])
In [25]: np.empty((2, 3, 2))
Out[25]:
array([[[  4.94065646e-324,       4.94065646e-324],
        [  3.87491056e-297,       2.46845796e-130],
        [  4.94065646e-324,       4.94065646e-324]],
 
        [[ 1.90723115e+083,       5.73293533e-053],
        [ -2.33568637e+124,  -6.70608105e-012],
        [  4.42786966e+160,       1.27100354e+025]]])

警告：认为np.empty会返回全0数组的想法是不安全的。很多情况下（如前所示），它返回的都是一些未初始化的垃圾值。

arange是Python内置函数range的数组版：

In [26]: np.arange(15)
Out[26]: array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])

表4-1列出了一些数组创建函数。由于NumPy关注的是数值计算，因此，如果没有特别指定，数据类型基本都是float64（浮点数）。

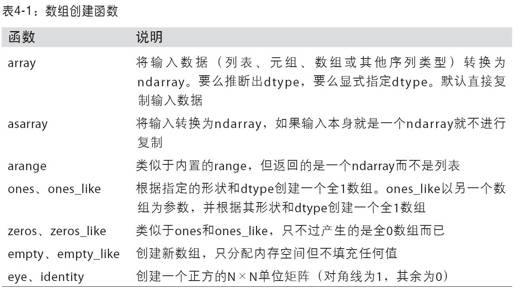
NumPy的ndarray：一种多维数组对象 - 图1

ndarray的数据类型

dtype（数据类型）是一个特殊的对象，它含有ndarray将一块内存解释为特定数据类型所需的信息：

In [27]: arr1 = np.array([1, 2, 3], dtype=np.float64)
 
In [28]: arr2 = np.array([1, 2, 3], dtype=np.int32)
 
In [29]: arr1.dtype             In [30]: arr2.dtype
Out[29]: dtype('float64')       Out[30]: dtype('int32')

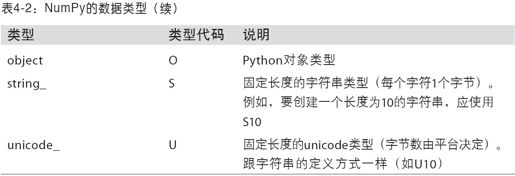
dtype是NumPy如此强大和灵活的原因之一。多数情况下，它们直接映射到相应的机器表示，这使得“读写磁盘上的二进制数据流”以及“集成低级语言代码（如C、Fortran）”等工作变得更加简单。数值型dtype的命名方式相同：一个类型名（如float或int），后面跟一个用于表示各元素位长的数字。标准的双精度浮点值（即Python中的float对象）需要占用8字节（即64位）。因此，该类型在NumPy中就记作float64。表4-2列出了NumPy所支持的全部数据类型。

注意：记不住这些NumPy的dtype也没关系，新手更是如此。通常只需要知道你所处理的数据的大致类型是浮点数、复数、整数、布尔值、字符串，还是普通的Python对象即可。当你需要控制数据在内存和磁盘中的存储方式时（尤其是对大数据集），那就得了解如何控制存储类型。

NumPy的ndarray：一种多维数组对象 - 图2

NumPy的ndarray：一种多维数组对象 - 图3

你可以通过ndarray的astype方法显式地转换其dtype：

In [31]: arr = np.array([1, 2, 3, 4, 5])
 
In [32]: arr.dtype
Out[32]: dtype('int64')
 
In [33]: float_arr = arr.astype(np.float64)
 
In [34]: float_arr.dtype
Out[34]: dtype('float64')

在本例中，整数被转换成了浮点数。如果将浮点数转换成整数，则小数部分将会被截断：

In [35]: arr = np.array([3.7, -1.2, -2.6, 0.5, 12.9, 10.1])
 
In [36]: arr
Out[36]: array([  3.7,  -1.2,  -2.6,       0.5,  12.9,  10.1])
 
In [37]: arr.astype(np.int32)
Out[37]: array([ 3, -1, -2,  0, 12, 10], dtype=int32)

如果某字符串数组表示的全是数字，也可以用astype将其转换为数值形式：

In [38]: numeric_strings = np.array(['1.25', '-9.6', '42'], dtype=np.string_)
 
In [39]: numeric_strings.astype(float)
Out[39]: array([  1.25,  -9.6 ,  42.  ])

如果转换过程因为某种原因而失败了（比如某个不能被转换为float64的字符串），就会引发一个TypeError。看到了吧，我比较懒，写的是float而不是np.float64；NumPy很聪明，它会将Python类型映射到等价的dtype上。

数组的dtype还有另外一个用法：

In [40]: int_array = np.arange(10)
 
In [41]: calibers = np.array([.22, .270, .357, .380, .44, .50], dtype=np.float64)
 
In [42]: int_array.astype(calibers.dtype)
Out[42]: array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.])

你还可以用简洁的类型代码来表示dtype：

In [43]: empty_uint32 = np.empty(8, dtype='u4')
 
In [44]: empty_uint32
Out[44]:
array([       0,        0, 65904672,      0, 64856792,   0,
       39438163,       0], dtype=uint32)

注意：调用astype无论如何都会创建出一个新的数组（原始数据的一份拷贝），即使新dtype跟老dtype相同也是如此。

警告：注意，浮点数（比如float64和float32）只能表示近似的分数值。在复杂计算中，由于可能会积累一些浮点错误，因此比较操作只能在一定小数位以内有效。

数组和标量之间的运算

数组很重要，因为它使你不用编写循环即可对数据执行批量运算。这通常就叫做矢量化（vectorization）。大小相等的数组之间的任何算术运算都会将运算应用到元素级：

In [45]: arr = np.array([[1., 2., 3.], [4., 5., 6.]])
 
In [46]: arr
Out[46]:
array([[ 1.,  2.,  3.],
       [ 4.,  5.,  6.]])
 
In [47]: arr * arr            In [48]: arr - arr
Out[47]:                      Out[48]:
array([[  1.,   4.,   9.],    array([[ 0.,  0.,  0.],
       [ 16.,  25.,  36.]])          [ 0.,  0.,  0.]])

同样，数组与标量的算术运算也会将那个标量值传播到各个元素：

In [49]: 1 / arr                        In [50]: arr ** 0.5
Out[49]:                                Out[50]:
array([[ 1.    ,  0.5   ,  0.3333],     array([[ 1.   ,  1.4142,  1.7321],
       [ 0.25  ,  0.2   ,  0.1667]])           [ 2.   ,  2.2361,  2.4495]])

不同大小的数组之间的运算叫做广播（broadcasting），我们将在第12章中对其进行详细讨论。本书的内容不需要对广播机制有多深的理解。

基本的索引和切片

NumPy数组的索引是一个内容丰富的主题，因为选取数据子集或单个元素的方式有很多。一维数组很简单。从表面上看，它们跟Python列表的功能差不多：

In [51]: arr = np.arange(10)
 
In [52]: arr
Out[52]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
 
In [53]: arr[5]
Out[53]: 5
 
In [54]: arr[5:8]
Out[54]: array([5, 6, 7])
 
In [55]: arr[5:8] = 12
 
In [56]: arr
Out[56]: array([ 0,  1,  2,  3,  4, 12, 12, 12,  8,  9])

如上所示，当你将一个标量值赋值给一个切片时（如arr[5:8]=12），该值会自动传播（也就说后面将会讲到的“广播”）到整个选区。跟列表最重要的区别在于，数组切片是原始数组的视图。这意味着数据不会被复制，视图上的任何修改都会直接反映到源数组上：

In [57]: arr_slice = arr[5:8]
 
In [58]: arr_slice[1] = 12345
 
In [59]: arr
Out[59]: array([   0,   1,   2,   3,   4,    12, 12345,   12,   8,   9])
 
In [60]: arr_slice[:] = 64
 
In [61]: arr
Out[61]: array([ 0,  1,  2,  3,  4, 64, 64, 64,  8,  9])

如果你刚开始接触NumPy，可能会对此感到惊讶（尤其是当你曾经用过其他热衷于复制数组数据的编程语言）。由于NumPy的设计目的是处理大数据，所以你可以想象一下，假如NumPy坚持要将数据复制来复制去的话会产生何等的性能和内存问题。

警告：如果你想要得到的是ndarray切片的一份副本而非视图，就需要显式地进行复制操作，例如arr[5:8].copy()。

对于高维度数组，能做的事情更多。在一个二维数组中，各索引位置上的元素不再是标量而是一维数组：

In [62]: arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
 
In [63]: arr2d[2]
Out[63]: array([7, 8, 9])

因此，可以对各个元素进行递归访问，但这样需要做的事情有点多。你可以传入一个以逗号隔开的索引列表来选取单个元素。也就是说，下面两种方式是等价的：

In [64]: arr2d[0][2]
Out[64]: 3
 
In [65]: arr2d[0, 2]
Out[65]: 3

图4-1说明了二维数组的索引方式。

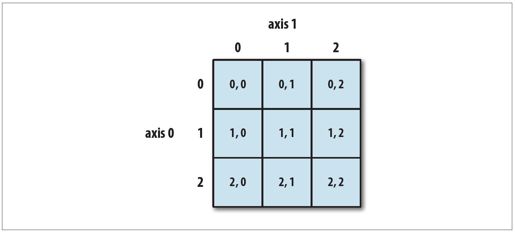
NumPy的ndarray：一种多维数组对象 - 图4

图4-1：NumPy数组中的元素索引

在多维数组中，如果省略了后面的索引，则返回对象会是一个维度低一点的ndarray（它含有高一级维度上的所有数据^译注1）。因此，在2×2×3数组arr3d中：

In [66]: arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
 
In [67]: arr3d
Out[67]:
array([[[ 1,  2,  3],
        [ 4,  5,  6]],
       [[ 7,  8,  9],
        [10, 11, 12]]])

arr3d[0]是一个2×3数组：

In [68]: arr3d[0]
Out[68]:
array([[1, 2, 3],
       [4, 5, 6]])

标量值和数组都可以被赋值给arr3d[0]：

In [69]: old_values = arr3d[0].copy()
 
In [70]: arr3d[0] = 42
 
In [71]: arr3d
Out[71]:
array([[[42, 42, 42],
        [42, 42, 42]],
       [[ 7,  8,  9],
        [10, 11, 12]]])
 
In [72]: arr3d[0] = old_values
 
In [73]: arr3d
Out[73]:
array([[[ 1,  2,  3],
        [ 4,  5,  6]],
       [[ 7,  8,  9],
        [10, 11, 12]]])

以此类推，arr3d[1,0]可以访问索引以(1,0)开头的那些值（以一维数组的形式返回）：

In [74]: arr3d[1, 0]
Out[74]: array([7, 8, 9])

注意，在上面所有这些选取数组子集的例子中，返回的数组都是视图。

切片索引

ndarray的切片语法跟Python列表这样的一维对象差不多：

In [75]: arr[1:6]
Out[75]: array([ 1,  2,  3,  4, 64])

高维度对象的花样更多，你可以在一个或多个轴上进行切片，也可以跟整数索引混合使用。对于上面那个二维数组arr2d，其切片方式稍显不同：

In [76]: arr2d            In [77]: arr2d[:2]
Out[76]:                  Out[77]:
array([[1, 2, 3],         array([[1, 2, 3],
       [4, 5, 6],               [4, 5, 6]])
       [7, 8, 9]])

可以看出，它是沿着第0轴（即第一个轴）切片的。也就是说，切片是沿着一个轴向选取元素的。你可以一次传入多个切片，就像传入多个索引那样：

In [78]: arr2d[:2, 1:]
Out[78]:
array([[2, 3],
       [5, 6]])

像这样进行切片时，只能得到相同维数的数组视图。通过将整数索引和切片混合，可以得到低维度的切片：

In [79]: arr2d[1, :2]        In [80]: arr2d[2, :1]
Out[79]: array([4, 5])       Out[80]: array([7])

图4-2对此进行了说明。注意，“只有冒号”表示选取整个轴，因此你可以像下面这样只对高维轴进行切片：

In [81]: arr2d[:, :1]
Out[81]:
array([[1],
       [4],
       [7]])

自然，对切片表达式的赋值操作也会被扩散到整个选区：

In [82]: arr2d[:2, 1:] = 0

布尔型索引

来看这样一个例子，假设我们有一个用于存储数据的数组以及一个存储姓名的数组（含有重复项）。在这里，我将使用numpy.random中的randn函数生成一些正态分布的随机数据：

In [83]: names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
 
In [84]: data = randn(7, 4)
 
In [85]: names
Out[85]:
array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'],
      dtype='|S4')
 
In [86]: data
Out[86]:
array([[-0.048 ,  0.5433, -0.2349,  1.2792],
       [-0.268 ,  0.5465,  0.0939, -2.0445],
       [-0.047 , -2.026 ,  0.7719,  0.3103],
       [ 2.1452,  0.8799, -0.0523,  0.0672],
       [-1.0023, -0.1698,  1.1503,  1.7289],
       [ 0.1913,  0.4544,  0.4519,  0.5535],
       [ 0.5994,  0.8174, -0.9297, -1.2564]])

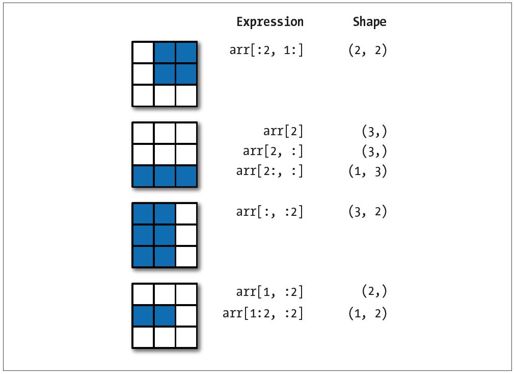
NumPy的ndarray：一种多维数组对象 - 图5

图4-2：二维数组切片

假设每个名字都对应data数组中的一行，而我们想要选出对应于名字"Bob"的所有行。跟算术运算一样，数组的比较运算（如==）也是矢量化的。因此，对names和字符串"Bob"的比较运算将会产生一个布尔型数组：

In [87]: names == 'Bob'
Out[87]: array([ True, False, False, True, False, False, False], dtype=bool)

这个布尔型数组可用于数组索引：

In [88]: data[names == 'Bob']
Out[88]:
array([[-0.048 ,  0.5433, -0.2349,  1.2792],
       [ 2.1452,  0.8799, -0.0523,  0.0672]])

布尔型数组的长度必须跟被索引的轴长度一致。此外，还可以将布尔型数组跟切片、整数（或整数序列，稍后将对此进行详细讲解）混合使用：

In [89]: data[names == 'Bob', 2:]
Out[89]:
array([[-0.2349,  1.2792],
       [-0.0523,  0.0672]])
 
In [90]: data[names == 'Bob', 3]
Out[90]: array([ 1.2792,  0.0672])

要选择除"Bob"以外的其他值，既可以使用不等于符号（!=），也可以通过负号（－）对条件进行否定：

In [91]: names != 'Bob'
Out[91]: array([False, True, True, False, True, True, True], dtype=bool)
 
In [92]: data[-(names == 'Bob')]
Out[92]:
array([[-0.268 ,  0.5465,  0.0939, -2.0445],
       [-0.047 , -2.026 ,  0.7719,  0.3103],
       [-1.0023, -0.1698,  1.1503,  1.7289],
       [ 0.1913,  0.4544,  0.4519,  0.5535],
       [ 0.5994,  0.8174, -0.9297, -1.2564]])

选取这三个名字中的两个需要组合应用多个布尔条件，使用&（和）、|（或）之类的布尔算术运算符即可：

In [93]: mask = (names == 'Bob') | (names == 'Will')
 
In [94]: mask
Out[94]: array([True, False, True, True, True, False, False], dtype=bool)
 
In [95]: data[mask]
Out[95]:
array([[-0.048 ,  0.5433, -0.2349,  1.2792],
       [-0.047 , -2.026 ,  0.7719,  0.3103],
       [ 2.1452,  0.8799, -0.0523,  0.0672],
       [-1.0023, -0.1698,  1.1503,  1.7289]])

通过布尔型索引选取数组中的数据，将总是创建数据的副本，即使返回一模一样的数组也是如此。

警告： Python关键字and和or在布尔型数组中无效。

通过布尔型数组设置值是一种经常用到的手段。为了将data中的所有负值都设置为0，我们只需：

In [96]: data[data < 0] = 0
 
In [97]: data
Out[97]:
array([[ 0.         ,  0.5433,  0.    ,  1.2792],
       [ 0.         ,  0.5465,  0.0939,  0.    ],
       [ 0.         ,  0.    ,  0.7719,  0.3103],
       [ 2.1452,  0.8799,  0.    ,  0.0672],
       [ 0.         ,  0.    ,  1.1503,  1.7289],
       [ 0.1913,  0.4544,  0.4519,  0.5535],
       [ 0.5994,  0.8174,  0.    ,  0.    ]])

通过一维布尔数组设置整行或列的值也很简单：

In [98]: data[names != 'Joe'] = 7
 
In [99]: data
Out[99]:
array([[ 7.    ,  7.    ,  7.    ,  7.    ],
       [ 0.    ,  0.5465,  0.0939,  0.    ],
       [ 7.    ,  7.    ,  7.    ,  7.    ],
       [ 7.    ,  7.    ,  7.    ,  7.    ],
       [ 7.    ,  7.    ,  7.    ,  7.    ],
       [ 0.1913,  0.4544,  0.4519,  0.5535],
       [ 0.5994,  0.8174,  0.    ,  0.    ]])

花式索引

花式索引（Fancy indexing）是一个NumPy术语，它指的是利用整数数组进行索引。假设我们有一个8×4数组：

In [100]: arr = np.empty((8, 4))
 
In [101]: for i in range(8):
    ....:     arr[i] = i
 
In [102]: arr
Out[102]:
array([[ 0.,  0.,  0.,  0.],
       [ 1.,  1.,  1.,  1.],
       [ 2.,  2.,  2.,  2.],
       [ 3.,  3.,  3.,  3.],
       [ 4.,  4.,  4.,  4.],
       [ 5.,  5.,  5.,  5.],
       [ 6.,  6.,  6.,  6.],
       [ 7.,  7.,  7.,  7.]])

为了以特定顺序选取行子集，只需传入一个用于指定顺序的整数列表或ndarray即可：

In [103]: arr[[4, 3, 0, 6]]
Out[103]:
array([[ 4.,  4.,  4.,  4.],
       [ 3.,  3.,  3.,  3.],
       [ 0.,  0.,  0.,  0.],
       [ 6.,  6.,  6.,  6.]])

这段代码确实达到我们的要求了！使用负数索引将会从末尾开始选取行：

In [104]: arr[[-3, -5, -7]]
Out[104]:
array([[ 5.,  5.,  5.,  5.],
       [ 3.,  3.,  3.,  3.],
       [ 1.,  1.,  1.,  1.]])

一次传入多个索引数组会有一点特别。它返回的是一个一维数组，其中的元素对应各个索引元组：

#有关reshape的知识将在第12章中讲解
In [105]: arr = np.arange(32).reshape((8, 4))
 
In [106]: arr
Out[106]:
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])
 
In [107]: arr[[1, 5, 7, 2], [0, 3, 1, 2]]
Out[107]: array([ 4, 23, 29, 10])

我们来看看具体是怎么一回事。最终选出的是元素(1,0)、(5,3)、(7,1)和(2,2)。这个花式索引的行为可能会跟某些用户的预期不一样（包括我在内），选取矩阵的行列子集应该是矩形区域的形式才对。下面是得到该结果的一个办法：

In [108]: arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]
Out[108]:
array([[ 4,  7,  5,  6],
       [20, 23, 21, 22],
       [28, 31, 29, 30],
       [ 8, 11,  9, 10]])

另外一个办法是使用np.ix_函数，它可以将两个一维整数数组转换为一个用于选取方形区域的索引器：

In [109]: arr[np.ix_([1, 5, 7, 2], [0, 3, 1, 2])]
Out[109]:
array([[ 4,  7,  5,  6],
       [20, 23, 21, 22],
       [28, 31, 29, 30],
       [ 8, 11,  9, 10]])

记住，花式索引跟切片不一样，它总是将数据复制到新数组中。

数组转置和轴对换

转置（transpose）是重塑的一种特殊形式，它返回的是源数据的视图（不会进行任何复制操作）。数组不仅有transpose方法，还有一个特殊的T属性：

In [110]: arr = np.arange(15).reshape((3, 5))
 
In [111]: arr
Out[111]:
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])
In [112]: arr.T
Out[112]:
array([[ 0,  5, 10],
       [ 1,  6, 11],
       [ 2,  7, 12],
       [ 3,  8, 13],
       [ 4,  9, 14]])

在进行矩阵计算时，经常需要用到该操作，比如利用np.dot计算矩阵内积X^TX：

In [113]: arr = np.random.randn(6, 3)
 
In [114]: np.dot(arr.T, arr)
Out[114]:
array([[ 2.584 ,    1.8753,   0.8888],
       [ 1.8753,    6.6636,   0.3884],
       [ 0.8888,    0.3884,   3.9781]])

对于高维数组，transpose需要得到一个由轴编号组成的元组才能对这些轴进行转置（比较费脑子）：

In [115]: arr = np.arange(16).reshape((2, 2, 4))
 
In [116]: arr
Out[116]:
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],
       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])
 
In [117]: arr.transpose((1, 0, 2))
Out[117]:
array([[[ 0,  1,  2,  3],
        [ 8,  9, 10, 11]],
       [[ 4,  5,  6,  7],
        [12, 13, 14, 15]]])

简单的转置可以使用.T，它其实就是进行轴对换而已。ndarray还有一个swapaxes方法，它需要接受一对轴编号：

In [118]: arr
Out[118]:
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],
 
       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])
In [119]: arr.swapaxes(1, 2)
Out[119]:
array([[[ 0,  4],
        [ 1,  5],
        [ 2,  6],
        [ 3,  7]],
 
       [[ 8, 12],
        [ 9, 13],
        [10, 14],
        [11, 15]]])

swapaxes也是返回源数据的视图（不会进行任何复制操作）。

译注1：括号外面的“维度”是一维、二维、三维、四维之类的意思，而括号里面的应该理解为“轴”。也就是说，这里指的是“返回的低维数组含有原始高维数组某条轴上的所有数据”。