利用数组进行数据处理

NumPy数组使你可以将许多种数据处理任务表述为简洁的数组表达式（否则需要编写循环）。用数组表达式代替循环的做法，通常被称为矢量化。一般来说，矢量化数组运算要比等价的纯Python方式快上一两个数量级（甚至更多），尤其是各种数值计算。在后面内容中（见第12章）我将介绍广播，这是一种针对矢量化计算的强大手段。

假设我们想要在一组值（网格型）上计算函数sqrt(x^2+y^2)。np.meshgrid函数接受两个一维数组，并产生两个二维矩阵（对应于两个数组中所有的(x,y)对）：

  1. In [130]: points = np.arange(-5, 5, 0.01) # 1000个间隔相等的点
  2.  
  3. In [131]: xs, ys = np.meshgrid(points, points)
  4.  
  5. In [132]: ys
  6. Out[132]:
  7. array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
  8.        [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
  9.        [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
  10.        ...,
  11.        [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
  12.        [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
  13.        [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

现在，对该函数的求值运算就好办了，把这两个数组当做两个浮点数那样编写表达式即可：

  1. In [134]: import matplotlib.pyplot as plt
  2.  
  3. In [135]: z = np.sqrt(xs ** 2 + ys ** 2)
  4.  
  5. In [136]: z
  6. Out[136]:
  7. array([[ 7.0711,   7.064 ,   7.0569, ...,   7.0499,   7.0569,   7.064 ],
  8.        [ 7.064 ,   7.0569,   7.0499, ...,   7.0428,   7.0499,   7.0569],
  9.        [ 7.0569,   7.0499,   7.0428, ...,   7.0357,   7.0428,   7.0499],
  10.        ...,
  11.        [ 7.0499,   7.0428,   7.0357, ...,   7.0286,   7.0357,   7.0428],
  12.        [ 7.0569,   7.0499,   7.0428, ...,   7.0357,   7.0428,   7.0499],
  13.        [ 7.064 ,   7.0569,   7.0499, ...,   7.0428,   7.0499,   7.0569]])
  14.  
  15. In [137]: plt.imshow(z, cmap=plt.cm.gray); plt.colorbar()
  16. Out[137]: <matplotlib.colorbar.Colorbar instance at 0x4e46d40>
  17.  
  18. In [138]: plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
  19. Out[138]: <matplotlib.text.Text at 0x4565790>

函数值（一个二维数组）的图形化结果如图4-3所示。这张图我是用matplotlib的imshow函数创建的。

将条件逻辑表述为数组运算

numpy.where函数是三元表达式x if condition else y的矢量化版本。假设我们有一个布尔数组和两个值数组：

  1. In [140]: xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
  2.  
  3. In [141]: yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
  4.  
  5. In [142]: cond = np.array([True, False, True, True, False])

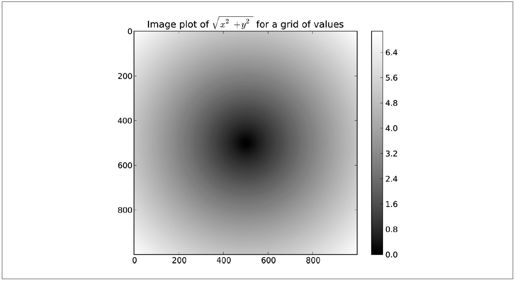
利用数组进行数据处理 - 图1

图4-3：根据网格对函数求值的结果

假设我们想要根据cond中的值选取xarr和yarr的值：当cond中的值为True时，选取xarr的值，否则从yarr中选取。列表推导式的写法应该如下所示：

  1. In [143]: result = [(x if c else y)
  2. 　　 ...:               for x, y, c in zip(xarr, yarr, cond)]
  3.  
  4. In [144]: result
  5. Out[144]: [1.1000000000000001, 2.2000000000000002, 1.3, 1.3999999999999999, 2.5]

这有几个问题。第一，它对大数组的处理速度不是很快（因为所有工作都是由纯Python完成的）。第二，无法用于多维数组。若使用np.where，则可以将该功能写得非常简洁：

  1. In [145]: result = np.where(cond, xarr, yarr)
  2.  
  3. In [146]: result
  4. Out[146]: array([ 1.1,  2.2,  1.3,  1.4,  2.5])

np.where的第二个和第三个参数不必是数组，它们都可以是标量值。在数据分析工作中，where通常用于根据另一个数组而产生一个新的数组。假设有一个由随机数据组成的矩阵，你希望将所有正值替换为2，将所有负值替换为－2。若利用np.where，则会非常简单：

  1. In [147]: arr = randn(4, 4)
  2.  
  3. In [148]: arr
  4. Out[148]:
  5. array([[ 0.6372,  2.2043,  1.7904,  0.0752],
  6.        [-1.5926, -1.1536,  0.4413,  0.3483],
  7.        [-0.1798,  0.3299,  0.7827, -0.7585],
  8.        [ 0.5857,  0.1619,  1.3583, -1.3865]])
  9.  
  10. In [149]: np.where(arr > 0, 2, -2)
  11. Out[149]:
  12. array([[ 2,  2,  2,  2],
  13.        [-2, -2,  2,  2],
  14.        [-2,  2,  2, -2],
  15.        [ 2,  2,  2, -2]])
  16.  
  17. In [150]: np.where(arr > 0, 2, arr) # 只将正值设置为2
  18. Out[150]:
  19. array([[ 2.    ,  2.    ,       2.    ,  2.    ],
  20.        [-1.5926, -1.1536,       2.    ,  2.    ],
  21.        [-0.1798,  2.    ,       2.    , -0.7585],
  22.        [ 2.    ,  2.    ,       2.    , -1.3865]])

传递给where的数组大小可以不相等，甚至可以是标量值。

只要稍微动动脑子，你就能用where表述出更复杂的逻辑。想象一下这样一个例子，我有两个布尔型数组cond1和cond2，希望根据4种不同的布尔值组合实现不同的赋值操作：

  1. result = []
  2. for i in range(n):
  3.     if cond1[i] and cond2[i]:
  4.         result.append(0)
  5.     elif cond1[i]:
  6.         result.append(1)
  7.     elif cond2[i]:
  8.         result.append(2)
  9.     else:
  10.         result.append(3)

虽然不是非常明显，但这个for循环确实可以被改写成一个嵌套的where表达式：

  1. np.where(cond1 & cond2, 0,
  2.            np.where(cond1, 1,
  3.                       np.where(cond2, 2, 3)))

在这个特殊的例子中，我们还可以利用“布尔值在计算过程中可以被当做0或1处理”这个事实，所以还能将其写成下面这样的算术运算（虽然看上去有点神秘）：

  1. result = 1 * (cond1 -cond2) + 2 * (cond2 & -cond1) + 3 * -(cond1 | cond2)

数学和统计方法

可以通过数组上的一组数学函数对整个数组或某个轴向的数据进行统计计算。sum、mean以及标准差std等聚合计算（aggregation，通常叫做约简（reduction））既可以当做数组的实例方法调用，也可以当做顶级NumPy函数使用：

  1. In [151]: arr = np.random.randn(5, 4) # 正态分布的数据
  2.  
  3. In [152]: arr.mean()
  4. Out[152]: 0.062814911084854597
  5.  
  6. In [153]: np.mean(arr)
  7. Out[153]: 0.062814911084854597
  8.  
  9. In [154]: arr.sum()
  10. Out[154]: 1.2562982216970919

mean和sum这类的函数可以接受一个axis参数（用于计算该轴向上的统计值），最终结果是一个少一维的数组：

  1. In [155]: arr.mean(axis=1)
  2. Out[155]: array([-1.2833,  0.2844,  0.6574,  0.6743, -0.0187])
  3.  
  4. In [156]: arr.sum(0)
  5. Out[156]: array([-3.1003, -1.6189,  1.4044,  4.5712])

其他如cumsum和cumprod之类的方法则不聚合，而是产生一个由中间结果组成的数组：

  1. In [157]: arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
  2.  
  3. In [158]: arr.cumsum(0)
  4. Out[158]:
  5. array([[ 0,  1,  2],
  6.        [ 3,  5,  7],
  7.        [ 9, 12, 15]])
  8. In [159]: arr.cumprod(1)
  9. Out[159]:
  10. array([[  0,   0,   0],
  11.        [  3,  12,  60],
  12.        [  6,  42, 336]])

表4-5列出了全部的基本数组统计方法。后续章节中有很多例子都会用到这些方法。

利用数组进行数据处理 - 图2

利用数组进行数据处理 - 图3

用于布尔型数组的方法

在上面这些方法中，布尔值会被强制转换为1（True）和0（False）。因此，sum经常被用来对布尔型数组中的True值计数：

  1. In [160]: arr = randn(100)
  2.  
  3. In [161]: (arr > 0).sum() # 正值的数量
  4. Out[161]: 44

另外还有两个方法any和all，它们对布尔型数组非常有用。any用于测试数组中是否存在一个或多个True，而all则检查数组中所有值是否都是True：

  1. In [162]: bools = np.array([False, False, True, False])
  2.  
  3. In [163]: bools.any()
  4. Out[163]: True
  5.  
  6. In [164]: bools.all()
  7. Out[164]: False

这两个方法也能用于非布尔型数组，所有非0元素将会被当做True。

排序

跟Python内置的列表类型一样，NumPy数组也可以通过sort方法就地排序：

  1. In [165]: arr = randn(8)
  2.  
  3. In [166]: arr
  4. Out[166]:
  5. array([ 0.6903,  0.4678,  0.0968, -0.1349,  0.9879,  0.0185,  -1.3147,  -0.5425])
  6.  
  7. In [167]: arr.sort()
  8. In [168]: arr
  9. Out[168]:
  10. array([-1.3147, -0.5425, -0.1349,  0.0185,  0.0968,  0.4678,  0.6903,  0.9879])

多维数组可以在任何一个轴向上进行排序，只需将轴编号传给sort即可：

  1. In [169]: arr = randn(5, 3)
  2.  
  3. In [170]: arr
  4. Out[170]:
  5. array([[-0.7139, -1.6331, -0.4959],
  6.        [ 0.8236, -1.3132, -0.1935],
  7.        [-1.6748,  3.0336, -0.863 ],
  8.        [-0.3161,  0.5362, -2.468 ],
  9.        [ 0.9058,  1.1184, -1.0516]])
  10.  
  11. In [171]: arr.sort(1)
  12.  
  13. In [172]: arr
  14. Out[172]:
  15. array([[-1.6331, -0.7139, -0.4959],
  16.        [-1.3132, -0.1935,  0.8236],
  17.        [-1.6748, -0.863 ,  3.0336],
  18.        [-2.468 , -0.3161,  0.5362],
  19.        [-1.0516,  0.9058,  1.1184]])

顶级方法np.sort返回的是数组的已排序副本，而就地排序则会修改数组本身。计算数组分位数最简单的办法是对其进行排序，然后选取特定位置的值：

  1. In [173]: large_arr = randn(1000)
  2.  
  3. In [174]: large_arr.sort()
  4.  
  5. In [175]: large_arr[int(0.05 * len(large_arr))] # 5%分位数
  6. Out[175]: -1.5791023260896004

更多关于NumPy排序方法以及诸如间接排序之类的高级技术，请参阅第12章。在pandas中还可以找到一些其他跟排序有关的数据操作（比如根据一列或多列对表格型数据进行排序）。

唯一化以及其他的集合逻辑

NumPy提供了一些针对一维ndarray的基本集合运算。最常用的可能要数np.unique了，它用于找出数组中的唯一值并返回已排序的结果：

  1. In [176]: names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
  2.  
  3. In [177]: np.unique(names)
  4. Out[177]:
  5. array(['Bob', 'Joe', 'Will'],
  6.       dtype='|S4')
  7.  
  8. In [178]: ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
  9.  
  10. In [179]: np.unique(ints)
  11. Out[179]: array([1, 2, 3, 4])

拿跟np.unique等价的纯Python代码来对比一下：

  1. In [180]: sorted(set(names))
  2. Out[180]: ['Bob', 'Joe', 'Will']

另一个函数np.in1d用于测试一个数组中的值在另一个数组中的成员资格，返回一个布尔型数组：

  1. In [181]: values = np.array([6, 0, 0, 3, 2, 5, 6])
  2.  
  3. In [182]: np.in1d(values, [2, 3, 6])
  4. Out[182]: array([ True, False, False,  True,  True, False,  True], dtype=bool)

NumPy中的集合函数请参见表4-6。

利用数组进行数据处理 - 图4

译注2：简单点说，就是“异或”。