分组变换和分析

在第9章中，我们学习了分组统计计算的基础知识，还学习了如何对数据集的分组应用自定义的变换函数。

下面以一组假想的股票投资组合为例。首先我随机生成1000个股票代码：

  1. import random; random.seed(0)
  2. import string
  3.  
  4. N = 1000
  5. def rands(n):
  6.     choices = string.ascii_uppercase
  7.     return ''.join([random.choice(choices) for _ in xrange(n)])
  8. tickers = np.array([rands(5) for _ in xrange(N)])

然后创建一个含有3列的DataFrame来承载这些假想数据，不过只选择部分股票组成该投资组合：

  1. M = 500
  2. df = DataFrame({'Momentum' : np.random.randn(M) / 200 + 0.03,
  3.                 'Value' : np.random.randn(M) / 200 + 0.08,
  4.                 'ShortInterest' : np.random.randn(M) / 200 - 0.02},
  5.                  index=tickers[:M])

接下来，我们为这些股票随机创建一个行业分类。为了简单起见，我只选用了两个行业，并将映射关系保存在Series中：

  1. ind_names = np.array(['FINANCIAL', 'TECH'])
  2. sampler = np.random.randint(0, len(ind_names), N)
  3. industries = Series(ind_names[sampler], index=tickers,
  4.                     name='industry')

现在，我们就可以根据行业分类进行分组并执行分组聚合和变换了：

  1. In [90]: by_industry = df.groupby(industries)
  2.  
  3. In [91]: by_industry.mean()
  4. Out[91]:
  5.            Momentum  ShortInterest     Value
  6. industry
  7. FINANCIAL  0.029485      -0.020739  0.079929
  8. TECH       0.030407      -0.019609  0.080113
  9.  
  10. In [92]: by_industry.describe()
  11. Out[92]:
  12.                        Momentum     ShortInterest          Value
  13. industry
  14. FINANCIAL    count   246.000000246.000000     246.000000
  15.              mean      0.029485         -0.020739       0.079929
  16.              std       0.004802          0.004986       0.004548
  17.              min       0.017210         -0.036997       0.067025
  18.              25%       0.026263         -0.024138       0.076638
  19.              50%       0.029261         -0.020833       0.079804
  20.              75%       0.032806         -0.017345       0.082718
  21.              max       0.045884         -0.006322       0.093334
  22. TECH         count   254.000000        254.000000     254.000000
  23.              mean      0.030407         -0.019609       0.080113
  24.              std       0.005303          0.005074       0.004886
  25.              min       0.016778         -0.032682       0.065253
  26.              25%       0.026456         -0.022779       0.076737
  27.              50%       0.030650         -0.019829       0.080296
  28.              75%       0.033602         -0.016923       0.083353
  29.              max       0.049638         -0.003698       0.093081

要对这些按行业分组的投资组合进行各种变换，我们可以编写自定义的变换函数。例如行业内标准化处理，它广泛用于股票资产投资组合的构建过程：

  1. # 行业内标准化处理
  2. def zscore(group):
  3.     return (group - group.mean()) / group.std()
  4.  
  5. df_stand = by_industry.apply(zscore)

这样处理之后，各行业的平均值为0，标准差为1：

  1. In [94]: df_stand.groupby(industries).agg(['mean', 'std'])
  2. Out[94]:
  3.                Momentum       ShortInterest            Value
  4.                    mean  std           mean  std        mean  std
  5. industry
  6. FINANCIAL             0    1              0    1           0    1
  7. TECH                 -0    1             -0    1          -0    1

内置变换函数（如rank）的用法会更简洁一些：

  1. # 行业内降序排名
  2. In [95]: ind_rank = by_industry.rank(ascending=False)
  3.  
  4. In [96]: ind_rank.groupby(industries).agg(['min', 'max'])
  5. Out[96]:
  6.            Momentum       ShortInterest       Value
  7.                 min  max            min  max    min  max
  8. industry
  9. FINANCIAL         1  246              1  246      1  246
  10. TECH              1  254              1  254      1  254

在股票投资组合的定量分析中，“排名和标准化”是一种很常见的变换运算组合。通过将rank和zscore链接在一起即可完成整个变换过程，就像下面这样：

  1. # 行业内排名和标准化
  2. In [97]: by_industry.apply(lambda x: zscore(x.rank()))
  3. Out[97]:
  4. <class 'pandas.core.frame.DataFrame'>
  5. Index: 500 entries, VTKGN to PTDQE
  6. Data columns:
  7. Momentum         500  non-null values
  8. ShortInterest    500  non-null values
  9. Value            500  non-null values
  10. dtypes: float64(3)

分组因子暴露

因子分析（factor analysis）是投资组合定量管理中的一种技术。投资组合的持有量和性能（收益与损失）可以被分解为一个或多个表示投资组合权重的因子（风险因子就是其中之一）。例如，某只股票的价格与某个基准（比如标准普尔500指数）的协动性被称作其贝塔风险系数（beta，一种常见的风险因子）。下面以一个人为构成的投资组合为例进行讲解，它由三个随机生成的因子（通常称为因子载荷）和一些权重构成：

  1. from numpy.random import rand
  2. fac1, fac2, fac3 = np.random.rand(3, 1000)
  3.  
  4. ticker_subset = tickers.take(np.random.permutation(N)[:1000])
  5.  
  6. # 因子加权和以及噪声
  7. port = Series(0.7 * fac1 - 1.2 * fac2 + 0.3 * fac3 + rand(1000),
  8.               index=ticker_subset)
  9. factors = DataFrame({'f1': fac1, 'f2': fac2, 'f3': fac3},
  10.                      index=ticker_subset)

各因子与投资组合之间的矢量相关性可能说明不了什么问题：

  1. In [99]: factors.corrwith(port)
  2. Out[99]:
  3. f1    0.402377
  4. f2   -0.680980
  5. f3    0.168083

计算因子暴露的标准方式是最小二乘回归。使用pandas.ols（将factors作为解释变量）即可计算出整个投资组合的暴露：

  1. In [100]: pd.ols(y=port, x=factors).beta
  2. Out[100]:
  3. f1           0.761789
  4. f2          -1.208760
  5. f3           0.289865
  6. intercept    0.484477

不难看出，由于没有给投资组合添加过多的随机噪声，所以原始的因子权重基本上可算是恢复出来了。还可以通过groupby计算各行业的暴露量。为了达到这个目的，我先编写了一个函数，如下所示：

  1. def beta_exposure(chunk, factors=None):
  2.     return pd.ols(y=chunk, x=factors).beta

然后根据行业进行分组，并应用该函数，传入因子载荷的DataFrame：

  1. In [102]: by_ind = port.groupby(industries)
  2.  
  3. In [103]: exposures = by_ind.apply(beta_exposure, factors=factors)
  4.  
  5. In [104]: exposures.unstack()
  6. Out[104]:
  7.                  f1        f2        f3  intercept
  8. industry
  9. FINANCIAL  0.790329 -1.182970  0.275624   0.455569
  10. TECH       0.740857 -1.232882  0.303811   0.508188

十分位和四分位分析

基于样本分位数的分析是金融分析师们的另一个重要工具。例如，股票投资组合的性能可以根据各股的市盈率被划分入四分位（四个大小相等的块）。通过pandas.qcut和groupby可以非常轻松地实现分位数分析。

在下面这个例子中，我们利用跟随策略或动量交易策略通过SPY交易所交易基金买卖标准普尔500指数。你可以从Yahoo!Finance下载价格历史：

  1. In [105]: import pandas.io.data as web
  2.  
  3. In [106]: data = web.get_data_yahoo('SPY', '2006-01-01')译注5
  4.  
  5. In [107]: data
  6. Out[107]:
  7. <class 'pandas.core.frame.DataFrame'>
  8. DatetimeIndex: 1655 entries, 2006-01-03 00:00:00 to 2012-07-27 00:00:00
  9. Data columns:
  10. Open         1655  non-null values
  11. High         1655  non-null values
  12. Low          1655  non-null values
  13. Close        1655  non-null values
  14. Volume       1655  non-null values
  15. Adj Close    1655  non-null values
  16. dtypes: float64(5), int64(1)

接下来计算日收益率，并编写一个用于将收益率变换为趋势信号（通过滞后移动形成）的函数：

  1. px = data['Adj Close']
  2. returns = px.pct_change()
  3.  
  4. def to_index(rets):
  5.     index = (1 + rets).cumprod()
  6.     first_loc = max(index.notnull().argmax() - 1, 0)
  7.     index.values[first_loc] = 1
  8.     return index
  9.  
  10. def trend_signal(rets, lookback, lag):
  11.     signal = pd.rolling_sum(rets, lookback, min_periods=lookback - 5)
  12.     return signal.shift(lag)

通过该函数，我们可以（单纯地）创建和测试一种根据每周五动量信号进行交易的交易策略。

  1. In [109]: signal = trend_signal(returns, 100, 3)
  2.  
  3. In [110]: trade_friday = signal.resample('W-FRI').resample('B', fill_method='ffill')
  4.  
  5. In [111]: trade_rets = trade_friday.shift(1) * returns

然后将该策略的收益率转换为一个收益指数，并绘制一张图表（如图11-1所示）：

  1. In [112]: to_index(trade_rets).plot()

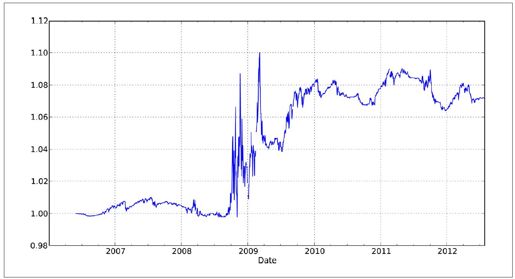
分组变换和分析 - 图1

图11-1：SPY动量策略收益指数

假如你希望将该策略的性能按不同大小的交易期波幅进行划分。年度标准差是计算波幅的一种简单办法，我们可以通过计算夏普比率来观察不同波动机制下的风险收益率：

  1. vol = pd.rolling_std(returns, 250, min_periods=200) * np.sqrt(250)
  2.  
  3. def sharpe(rets, ann=250):
  4.     return rets.mean() / rets.std()  * np.sqrt(ann)

现在，利用qcut将vol划分为四等份，并用sharpe进行聚合：

  1. In [114]: trade_rets.groupby(pd.qcut(vol, 4)).agg(sharpe)
  2. Out[114]:
  3. [0.0955, 0.16]    0.490051
  4. (0.16, 0.188]     0.482788
  5. (0.188, 0.231]   -0.731199
  6. (0.231, 0.457]    0.570500

这个结果说明，该策略在波幅最高时性能最好。

译注5：跟前面说的一样，这里最好还是加上截止日期，否则数据会比书上介绍的多。